// @(#)root/hist:$Name: $:$Id: TH1.cxx,v 1.253 2005/09/13 07:54:28 brun Exp $
// Author: Rene Brun 26/12/94
/*************************************************************************
* Copyright (C) 1995-2000, Rene Brun and Fons Rademakers. *
* All rights reserved. *
* *
* For the licensing terms see $ROOTSYS/LICENSE. *
* For the list of contributors see $ROOTSYS/README/CREDITS. *
*************************************************************************/
#include <stdlib.h>
#include <string.h>
#include <stdio.h>
#include <ctype.h>
#include "Riostream.h"
#include "TROOT.h"
#include "TH1.h"
#include "TH2.h"
#include "TF2.h"
#include "TF3.h"
#include "TVirtualPad.h"
#include "TRandom.h"
#include "TVirtualFitter.h"
#include "THLimitsFinder.h"
#include "TProfile.h"
#include "TStyle.h"
#include "TVectorF.h"
#include "TVectorD.h"
#include "TBrowser.h"
#include "TObjString.h"
//______________________________________________________________________________
// The H I S T O G R A M Classes
// ===============================
//
// ROOT supports the following histogram types:
//
// 1-D histograms:
// TH1C : histograms with one byte per channel. Maximum bin content = 255
// TH1S : histograms with one short per channel. Maximum bin content = 65535
// TH1I : histograms with one int per channel. Maximum bin content = 2147483647
// TH1F : histograms with one float per channel. Maximum precision 7 digits
// TH1D : histograms with one double per channel. Maximum precision 14 digits
//
// 2-D histograms:
// TH2C : histograms with one byte per channel. Maximum bin content = 255
// TH2S : histograms with one short per channel. Maximum bin content = 65535
// TH2I : histograms with one int per channel. Maximum bin content = 2147483647
// TH2F : histograms with one float per channel. Maximum precision 7 digits
// TH2D : histograms with one double per channel. Maximum precision 14 digits
//
// 3-D histograms:
// TH3C : histograms with one byte per channel. Maximum bin content = 255
// TH3S : histograms with one short per channel. Maximum bin content = 65535
// TH3I : histograms with one int per channel. Maximum bin content = 2147483647
// TH3F : histograms with one float per channel. Maximum precision 7 digits
// TH3D : histograms with one double per channel. Maximum precision 14 digits
//
// Profile histograms: See classes TProfile and TProfile2D
// Profile histograms are used to display the mean value of Y and its RMS
// for each bin in X. Profile histograms are in many cases an elegant
// replacement of two-dimensional histograms : the inter-relation of two
// measured quantities X and Y can always be visualized by a two-dimensional
// histogram or scatter-plot; If Y is an unknown (but single-valued)
// approximate function of X, this function is displayed by a profile
// histogram with much better precision than by a scatter-plot.
//
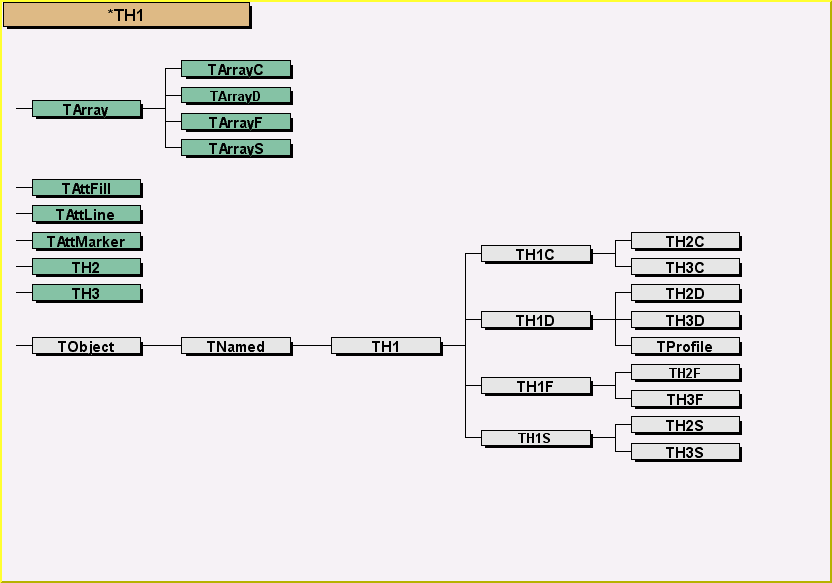
// - All histogram classes are derived from the base class TH1
//
// TH1
// ^
// |
// |
// |
// -----------------------------------------------------------
// | | | | | | |
// | | TH1C TH1S TH1I TH1F TH1D
// | | |
// | | |
// | TH2 TProfile
// | |
// | |
// | ----------------------------------
// | | | | | |
// | TH2C TH2S TH2I TH2F TH2D
// | |
// TH3 |
// | TProfile2D
// |
// -------------------------------------
// | | | | |
// TH3C TH3S TH3I TH3F TH3D
//
// The TH*C classes also inherit from the array class TArrayC.
// The TH*S classes also inherit from the array class TArrayS.
// The TH*I classes also inherit from the array class TArrayI.
// The TH*F classes also inherit from the array class TArrayF.
// The TH*D classes also inherit from the array class TArrayD.
//
// Creating histograms
// ===================
// Histograms are created by invoking one of the constructors, eg
// TH1F *h1 = new TH1F("h1","h1 title",100,0,4.4);
// TH2F *h2 = new TH2F("h2","h2 title",40,0,4,30,-3,3);
// histograms may also be created by:
// - calling the Clone function, see below
// - making a projection from a 2-D or 3-D histogram, see below
// - reading an histogram from a file
// When an histogram is created, a reference to it is automatically added
// to the list of in-memory objects for the current file or directory.
// This default behaviour can be changed by:
// h->SetDirectory(0); // for the current histogram h
// TH1::AddDirectory(kFALSE); // sets a global switch disabling the reference
// When the histogram is deleted, the reference to it is removed from
// the list of objects in memory.
// When a file is closed, all histograms in memory associated with this file
// are automatically deleted.
//
// Fix or variable bin size
// ========================
//
// All histogram types support either fix or variable bin sizes.
// 2-D histograms may have fix size bins along X and variable size bins
// along Y or vice-versa. The functions to fill, manipulate, draw or access
// histograms are identical in both cases.
// Each histogram always contains 3 objects TAxis: fXaxis, fYaxis and fZaxis
// To access the axis parameters, do:
// TAxis *xaxis = h->GetXaxis(); etc.
// Double_t binCenter = xaxis->GetBinCenter(bin), etc.
// See class TAxis for a description of all the access functions.
// The axis range is always stored internally in double precision.
//
// Convention for numbering bins
// =============================
// For all histogram types: nbins, xlow, xup
// bin = 0; underflow bin
// bin = 1; first bin with low-edge xlow INCLUDED
// bin = nbins; last bin with upper-edge xup EXCLUDED
// bin = nbins+1; overflow bin
// In case of 2-D or 3-D histograms, a "global bin" number is defined.
// For example, assuming a 3-D histogram with binx,biny,binz, the function
// Int_t gbin = h->GetBin(binx,biny,binz);
// returns a global/linearized gbin number. This global gbin is useful
// to access the bin content/error information independently of the dimension.
// Note that to access the information other than bin content and errors
// one should use the TAxis object directly with eg:
// Double_t xcenter = h3->GetZaxis()->GetBinCenter(27);
// returns the center along z of bin number 27 (not the global bin)
// in the 3-d histogram h3.
//
// Alphanumeric Bin Labels
// =======================
// By default, an histogram axis is drawn with its numeric bin labels.
// One can specify alphanumeric labels instead with:
// 1- call TAxis::SetBinLabel(bin,label);
// This can always be done before or after filling.
// When the histogram is drawn, bin labels will be automatically drawn.
// See example in $ROOTSYS/tutorials/labels1.C, labels2.C
// 2- call to a Fill function with one of the arguments being a string, eg
// hist1->Fill(somename,weigth);
// hist2->Fill(x,somename,weight);
// hist2->Fill(somename,y,weight);
// hist2->Fill(somenamex,somenamey,weight);
// See example in $ROOTSYS/tutorials/hlabels1.C, hlabels2.C
// 3- via TTree::Draw.
// see for example $ROOTSYS/tutorials/cern.C
// tree.Draw("Nation::Division"); where "Nation" and "Division"
// are two branches of a Tree.
// When using the options 2 or 3 above, the labels are automatically
// added to the list (THashList) of labels for a given axis.
// By default, an axis is drawn with the order of bins corresponding
// to the filling sequence. It is possible to reorder the axis
// - alphabetically
// - by increasing or decreasing values
// The reordering can be triggered via the TAxis contextMenu by selecting
// the menu item "LabelsOption" or by calling directly
// TH1::LabelsOption(option,axis) where
// -axis may be "X","Y" or "Z"
// -option may be:
// option = "a" sort by alphabetic order
// = ">" sort by decreasing values
// = "<" sort by increasing values
// = "h" draw labels horizonthal
// = "v" draw labels vertical
// = "u" draw labels up (end of label right adjusted)
// = "d" draw labels down (start of label left adjusted)
//
// When using the option 2 above, new labels are added by doubling the current
// number of bins in case one label does not exist yet.
// When the Filling is terminated, it is possible to trim the number
// of bins to match the number of active labels by calling
// TH1::LabelsDeflate(axis) with axis = "X","Y" or "Z"
// This operation is automatic when using TTree::Draw.
// Once bin labels have been created, they become persistent if the histogram
// is written to a file or when generating the C++ code via SavePrimitive.
//
// Histograms with automatic bins
// ==============================
// When an histogram is created with an axis lower limit greater or equal
// to its upper limit, the SetBuffer is automatically called with an
// argument fBufferSize equal to fgBufferSize (default value=1000).
// fgBufferSize may be reset via the static function TH1::SetDefaultBufferSize.
// The axis limits will be automatically computed when the buffer will
// be full or when the function BufferEmpty is called.
//
// Filling histograms
// ==================
// An histogram is typically filled with statements like:
// h1->Fill(x);
// h1->Fill(x,w); //fill with weight
// h2->Fill(x,y)
// h2->Fill(x,y,w)
// h3->Fill(x,y,z)
// h3->Fill(x,y,z,w)
// or via one of the Fill functions accepting names described above.
// The Fill functions compute the bin number corresponding to the given
// x,y or z argument and increment this bin by the given weight.
// The Fill functions return the bin number for 1-D histograms or global
// bin number for 2-D and 3-D histograms.
// If TH1::Sumw2 has been called before filling, the sum of squares of
// weights is also stored.
// One can also increment directly a bin number via TH1::AddBinContent
// or replace the existing content via TH1::SetBinContent.
// To access the bin content of a given bin, do:
// Double_t binContent = h->GetBinContent(bin);
//
// By default, the bin number is computed using the current axis ranges.
// If the automatic binning option has been set via
// h->SetBit(TH1::kCanRebin);
// then, the Fill Function will automatically extend the axis range to
// accomodate the new value specified in the Fill argument. The method
// used is to double the bin size until the new value fits in the range,
// merging bins two by two. This automatic binning options is extensively
// used by the TTree::Draw function when histogramming Tree variables
// with an unknown range.
// This automatic binning option is supported for 1-d, 2-D and 3-D histograms.
//
// During filling, some statistics parameters are incremented to compute
// the mean value and Root Mean Square with the maximum precision.
//
// In case of histograms of type TH1C, TH1S, TH2C, TH2S, TH3C, TH3S
// a check is made that the bin contents do not exceed the maximum positive
// capacity (127 or 65535). Histograms of all types may have positive
// or/and negative bin contents.
//
// Rebinning
// =========
// At any time, an histogram can be rebinned via TH1::Rebin. This function
// returns a new histogram with the rebinned contents.
// If bin errors were stored, they are recomputed during the rebinning.
//
// Associated errors
// =================
// By default, for each bin, the sum of weights is computed at fill time.
// One can also call TH1::Sumw2 to force the storage and computation
// of the sum of the square of weights per bin.
// If Sumw2 has been called, the error per bin is computed as the
// sqrt(sum of squares of weights), otherwise the error is set equal
// to the sqrt(bin content).
// To return the error for a given bin number, do:
// Double_t error = h->GetBinError(bin);
//
// Associated functions
// ====================
// One or more object (typically a TF1*) can be added to the list
// of functions (fFunctions) associated to each histogram.
// When TH1::Fit is invoked, the fitted function is added to this list.
// Given an histogram h, one can retrieve an associated function
// with: TF1 *myfunc = h->GetFunction("myfunc");
//
// Operations on histograms
// ========================
//
// Many types of operations are supported on histograms or between histograms
// - Addition of an histogram to the current histogram
// - Additions of two histograms with coefficients and storage into the current
// histogram
// - Multiplications and Divisions are supported in the same way as additions.
// - The Add, Divide and Multiply functions also exist to add,divide or multiply
// an histogram by a function.
// If an histogram has associated error bars (TH1::Sumw2 has been called),
// the resulting error bars are also computed assuming independent histograms.
// In case of divisions, Binomial errors are also supported.
//
//
// Fitting histograms
// ==================
//
// Histograms (1-D,2-D,3-D and Profiles) can be fitted with a user
// specified function via TH1::Fit. When an histogram is fitted, the
// resulting function with its parameters is added to the list of functions
// of this histogram. If the histogram is made persistent, the list of
// associated functions is also persistent. Given a pointer (see above)
// to an associated function myfunc, one can retrieve the function/fit
// parameters with calls such as:
// Double_t chi2 = myfunc->GetChisquare();
// Double_t par0 = myfunc->GetParameter(0); //value of 1st parameter
// Double_t err0 = myfunc->GetParError(0); //error on first parameter
//
//
// Projections of histograms
// ========================
// One can:
// - make a 1-D projection of a 2-D histogram or Profile
// see functions TH2::ProjectionX,Y, TH2::ProfileX,Y, TProfile::ProjectionX
// - make a 1-D, 2-D or profile out of a 3-D histogram
// see functions TH3::ProjectionZ, TH3::Project3D.
//
// One can fit these projections via:
// TH2::FitSlicesX,Y, TH3::FitSlicesZ.
//
// Random Numbers and histograms
// =============================
// TH1::FillRandom can be used to randomly fill an histogram using
// the contents of an existing TF1 function or another
// TH1 histogram (for all dimensions).
// For example the following two statements create and fill an histogram
// 10000 times with a default gaussian distribution of mean 0 and sigma 1:
// TH1F h1("h1","histo from a gaussian",100,-3,3);
// h1.FillRandom("gaus",10000);
// TH1::GetRandom can be used to return a random number distributed
// according the contents of an histogram.
//
// Making a copy of an histogram
// =============================
// Like for any other ROOT object derived from TObject, one can use
// the Clone() function. This makes an identical copy of the original
// histogram including all associated errors and functions, e.g.:
// TH1F *hnew = (TH1F*)h->Clone("hnew");
//
// Normalizing histograms
// ======================
// One can scale an histogram such that the bins integral is equal to
// the normalization parameter via TH1::Scale(Double_t norm).
//
// Drawing histograms
// ==================
// Histograms are drawn via the THistPainter class. Each histogram has
// a pointer to its own painter (to be usable in a multithreaded program).
// Many drawing options are supported.
// See THistPainter::Paint() for more details.
// The same histogram can be drawn with different options in different pads.
// When an histogram drawn in a pad is deleted, the histogram is
// automatically removed from the pad or pads where it was drawn.
// If an histogram is drawn in a pad, then filled again, the new status
// of the histogram will be automatically shown in the pad next time
// the pad is updated. One does not need to redraw the histogram.
// To draw the current version of an histogram in a pad, one can use
// h->DrawCopy();
// This makes a clone (see Clone below) of the histogram. Once the clone
// is drawn, the original histogram may be modified or deleted without
// affecting the aspect of the clone.
//
// One can use TH1::SetMaximum() and TH1::SetMinimum() to force a particular
// value for the maximum or the minimum scale on the plot.
//
// TH1::UseCurrentStyle() can be used to change all histogram graphics
// attributes to correspond to the current selected style.
// This function must be called for each histogram.
// In case one reads and draws many histograms from a file, one can force
// the histograms to inherit automatically the current graphics style
// by calling before gROOT->ForceStyle().
//
//
// Setting Drawing histogram contour levels (2-D hists only)
// =========================================================
// By default contours are automatically generated at equidistant
// intervals. A default value of 20 levels is used. This can be modified
// via TH1::SetContour() or TH1::SetContourLevel().
// the contours level info is used by the drawing options "cont", "surf",
// and "lego".
//
// Setting histogram graphics attributes
// =====================================
// The histogram classes inherit from the attribute classes:
// TAttLine, TAttFill, TAttMarker and TAttText.
// See the member functions of these classes for the list of options.
//
// Giving titles to the X, Y and Z axis
// ====================================
// h->GetXaxis()->SetTitle("X axis title");
// h->GetYaxis()->SetTitle("Y axis title");
// The histogram title and the axis titles can be any TLatex string.
// The titles are part of the persistent histogram.
// It is also possible to specify the histogram title and the axis
// titles at creation time. These titles can be given in the "title"
// parameter. They must be separated by ";":
// TH1F* h=new TH1F("h","Histogram title;X Axis;Y Axis;Z Axis",100,0,1);
// Any title can be omitted:
// TH1F* h=new TH1F("h","Histogram title;;Y Axis",100,0,1);
// TH1F* h=new TH1F("h",";;Y Axis",100,0,1);
// The method SetTitle has the same syntax:
// h->SetTitle("Histogram title;An other X title Axis");
//
// Saving/Reading histograms to/from a ROOT file
// =============================================
// The following statements create a ROOT file and store an histogram
// on the file. Because TH1 derives from TNamed, the key identifier on
// the file is the histogram name:
// TFile f("histos.root","new");
// TH1F h1("hgaus","histo from a gaussian",100,-3,3);
// h1.FillRandom("gaus",10000);
// h1->Write();
// To Read this histogram in another Root session, do:
// TFile f("histos.root");
// TH1F *h = (TH1F*)f.Get("hgaus");
// One can save all histograms in memory to the file by:
// file->Write();
//
// Miscelaneous operations
// =======================
//
// TH1::KolmogorovTest(): statistical test of compatibility in shape
// between two histograms
// TH1::Smooth() smooths the bin contents of a 1-d histogram
// TH1::Integral() returns the integral of bin contents in a given bin range
// TH1::GetMean(int axis) returns the mean value along axis
// TH1::GetRMS(int axis) returns the sigma distribution along axis
// TH1::GetEntries() returns the number of entries
// TH1::Reset() resets the bin contents and errors of an histogram
//
//
/*
 */
//
TF1 *gF1=0; //left for back compatibility (use TVirtualFitter::GetUserFunc instead)
const Int_t kNstat = 11;
Int_t TH1::fgBufferSize = 1000;
Bool_t TH1::fgAddDirectory = kTRUE;
Bool_t TH1::fgStatOverflows= kFALSE;
extern void H1InitGaus();
extern void H1InitExpo();
extern void H1InitPolynom();
extern void H1LeastSquareFit(Int_t n, Int_t m, Double_t *a);
extern void H1LeastSquareLinearFit(Int_t ndata, Double_t &a0, Double_t &a1, Int_t &ifail);
extern void H1LeastSquareSeqnd(Int_t n, Double_t *a, Int_t idim, Int_t &ifail, Int_t k, Double_t *b);
ClassImp(TH1)
//______________________________________________________________________________
TH1::TH1(): TNamed(), TAttLine(), TAttFill(), TAttMarker()
{
// -*-*-*-*-*-*-*-*-*Histogram default constructor*-*-*-*-*-*-*-*-*-*-*-*-*
// =============================
fDirectory = 0;
fFunctions = new TList;
fNcells = 0;
fIntegral = 0;
fPainter = 0;
fEntries = 0;
fNormFactor = 0;
fTsumw = fTsumw2=fTsumwx=fTsumwx2=0;
fMaximum = -1111;
fMinimum = -1111;
fBufferSize = 0;
fBuffer = 0;
fXaxis.SetName("xaxis");
fYaxis.SetName("yaxis");
fZaxis.SetName("zaxis");
fXaxis.SetParent(this);
fYaxis.SetParent(this);
fZaxis.SetParent(this);
UseCurrentStyle();
}
//______________________________________________________________________________
TH1::~TH1()
{
// -*-*-*-*-*-*-*-*-*Histogram default destructor*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ============================
//TH1 *junk = 0;
//junk->SetLineColor(0);
if (!TestBit(kNotDeleted)) return;
if (fIntegral) {delete [] fIntegral; fIntegral = 0;}
if (fBuffer) {delete [] fBuffer; fBuffer = 0;}
if (fFunctions) {
fFunctions->SetBit(kInvalidObject);
TObject *obj;
//special logic to support the case where the same object is
//added multiple times in fFunctions.
//This case happens when the same object is added with different
//drawing modes
//In the loop below we must be careful with objects (eg TCutG) that may
// have been added to the list of functions of several histograms
//and may have been already deleted.
while ((obj = fFunctions->First())) {
while(fFunctions->Remove(obj));
if (!obj->TestBit(kNotDeleted)) break;
delete obj;
}
delete fFunctions;
}
if (fDirectory) {
if (!fDirectory->TestBit(TDirectory::kCloseDirectory))
fDirectory->GetList()->Remove(this);
}
fFunctions = 0;
fDirectory = 0;
delete fPainter;
}
//______________________________________________________________________________
TH1::TH1(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
:TNamed(name,title), TAttLine(), TAttFill(), TAttMarker()
{
// -*-*-*-*-*-*-*Normal constructor for fix bin size histograms*-*-*-*-*-*-*
// ==============================================
//
// Creates the main histogram structure:
// name : name of histogram (avoid blanks)
// title : histogram title
// if title is of the form "stringt;stringx;stringy;stringz"
// the histogram title is set to stringt,
// the x axis title to stringy, the y axis title to stringy,etc
// nbins : number of bins
// xlow : low edge of first bin
// xup : upper edge of last bin (not included in last bin)
//
// When an histogram is created, it is automatically added to the list
// of special objects in the current directory.
// To find the pointer to this histogram in the current directory
// by its name, do:
// TH1F *h1 = (TH1F*)gDirectory->FindObject(name);
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Build();
if (nbins <= 0) nbins = 1;
fXaxis.Set(nbins,xlow,xup);
fNcells = fXaxis.GetNbins()+2;
}
//______________________________________________________________________________
TH1::TH1(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
:TNamed(name,title), TAttLine(), TAttFill(), TAttMarker()
{
// -*-*-*-*-*Normal constructor for variable bin size histograms*-*-*-*-*-*-*
// ===================================================
//
// Creates the main histogram structure:
// name : name of histogram (avoid blanks)
// title : histogram title
// if title is of the form "stringt;stringx;stringy;stringz"
// the histogram title is set to stringt,
// the x axis title to stringy, the y axis title to stringy,etc
// nbins : number of bins
// xbins : array of low-edges for each bin
// This is an array of size nbins+1
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Build();
if (nbins <= 0) nbins = 1;
if (xbins) fXaxis.Set(nbins,xbins);
else fXaxis.Set(nbins,0,1);
fNcells = fXaxis.GetNbins()+2;
}
//______________________________________________________________________________
TH1::TH1(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
:TNamed(name,title), TAttLine(), TAttFill(), TAttMarker()
{
// -*-*-*-*-*Normal constructor for variable bin size histograms*-*-*-*-*-*-*
// ===================================================
//
// Creates the main histogram structure:
// name : name of histogram (avoid blanks)
// title : histogram title
// if title is of the form "stringt;stringx;stringy;stringz"
// the histogram title is set to stringt,
// the x axis title to stringy, the y axis title to stringy,etc
// nbins : number of bins
// xbins : array of low-edges for each bin
// This is an array of size nbins+1
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Build();
if (nbins <= 0) nbins = 1;
if (xbins) fXaxis.Set(nbins,xbins);
else fXaxis.Set(nbins,0,1);
fNcells = fXaxis.GetNbins()+2;
}
//______________________________________________________________________________
TH1::TH1(const TH1 &h) : TNamed(), TAttLine(), TAttFill(), TAttMarker()
{
// Copy constructor.
// The list of functions is not copied. (Use Clone if needed)
Copy((TObject&)h);
}
//______________________________________________________________________________
Bool_t TH1::AddDirectoryStatus()
{
//static function: cannot be inlined on Windows/NT
return fgAddDirectory;
}
//______________________________________________________________________________
void TH1::Browse(TBrowser *b)
{
Draw(b ? b->GetDrawOption() : "");
gPad->Update();
}
//______________________________________________________________________________
void TH1::Build()
{
// -*-*-*-*-*-*-*-*Creates histogram basic data structure*-*-*-*-*-*-*-*-*-*
// ======================================
fDirectory = 0;
fPainter = 0;
fIntegral = 0;
fEntries = 0;
fNormFactor = 0;
fTsumw = fTsumw2=fTsumwx=fTsumwx2=0;
fMaximum = -1111;
fMinimum = -1111;
fBufferSize = 0;
fBuffer = 0;
fXaxis.SetName("xaxis");
fYaxis.SetName("yaxis");
fZaxis.SetName("zaxis");
fYaxis.Set(1,0.,1.);
fZaxis.Set(1,0.,1.);
fXaxis.SetParent(this);
fYaxis.SetParent(this);
fZaxis.SetParent(this);
SetTitle(fTitle.Data());
fFunctions = new TList;
UseCurrentStyle();
if (fgAddDirectory && gDirectory) {
if (!gDirectory->GetList()) {
Warning("Build","Current directory is not a valid directory");
return;
}
TH1 *hold = (TH1*)gDirectory->GetList()->FindObject(GetName());
if (hold) {
Warning("Build","Replacing existing histogram: %s (Potential memory leak).",GetName());
gDirectory->GetList()->Remove(hold);
hold->SetDirectory(0);
// delete hold;
}
gDirectory->Append(this);
fDirectory = gDirectory;
}
}
//______________________________________________________________________________
void TH1::Add(TF1 *f1, Double_t c1, Option_t *option)
{
// Performs the operation: this = this + c1*f1
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
//
// By default, the function is computed at the centre of the bin.
// if option "I" is specified (1-d histogram only), the integral of the
// function in each bin is used instead of the value of the function at
// the centre of the bin.
// Only bins inside the function range are recomputed.
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Add
if (!f1) {
Error("Add","Attempt to add a non-existing function");
return;
}
TString opt = option;
opt.ToLower();
Bool_t integral = kFALSE;
if (opt.Contains("i") && fDimension ==1) integral = kTRUE;
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// - Add statistics
Stat_t s1[10];
Int_t i;
for (i=0;i<10;i++) {s1[i] = 0;}
PutStats(s1);
SetMinimum();
SetMaximum();
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu=0;
Double_t xx[3];
Double_t *params = 0;
f1->InitArgs(xx,params);
for (binz=0;binz<=nbinsz+1;binz++) {
xx[2] = fZaxis.GetBinCenter(binz);
for (biny=0;biny<=nbinsy+1;biny++) {
xx[1] = fYaxis.GetBinCenter(biny);
for (binx=0;binx<=nbinsx+1;binx++) {
xx[0] = fXaxis.GetBinCenter(binx);
if (!f1->IsInside(xx)) continue;
TF1::RejectPoint(kFALSE);
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
if (integral) {
xx[0] = fXaxis.GetBinLowEdge(binx);
cu = c1*f1->EvalPar(xx);
cu += c1*f1->Integral(fXaxis.GetBinLowEdge(binx),fXaxis.GetBinUpEdge(binx))*fXaxis.GetBinWidth(binx);
} else {
cu = c1*f1->EvalPar(xx);
}
if (TF1::RejectedPoint()) continue;
Double_t error1 = GetBinError(bin);
AddBinContent(bin,cu);
if (fSumw2.fN) {
//errors are unchanged: error on f1 assumed 0
fSumw2.fArray[bin] = error1*error1;
}
}
}
}
}
//______________________________________________________________________________
void TH1::Add(const TH1 *h1, Double_t c1)
{
// Performs the operation: this = this + c1*h1
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
// Note that if h1 has Sumw2 set, Sumw2 is automatically called for this
// if not already set.
//
// IMPORTANT NOTE1: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Add
//
// IMPORTANT NOTE2: if h1 has a normalisation factor, the normalisation factor
// is used , ie this = this + c1*factor*h1
// Use the other TH1::Add function if you do not want this feature
if (!h1) {
Error("Add","Attempt to add a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()) {
Error("Add","Attempt to add histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Add","Attempt to add histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 has Sumw2 set
if (fSumw2.fN == 0 && h1->GetSumw2N() != 0) Sumw2();
// - Add statistics
fEntries += c1*h1->GetEntries();
Stat_t s1[kNstat], s2[kNstat];
Int_t i;
for (i=0;i<kNstat;i++) {s1[i] = s2[i] = 0;}
GetStats(s1);
h1->GetStats(s2);
for (i=0;i<kNstat;i++) {
if (i == 1) s1[i] += c1*c1*s2[i];
else s1[i] += c1*s2[i];
}
PutStats(s1);
SetMinimum();
SetMaximum();
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu;
Double_t factor =1;
if (h1->GetNormFactor() != 0) factor = h1->GetNormFactor()/h1->GetSumOfWeights();;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
cu = c1*factor*h1->GetBinContent(bin);
AddBinContent(bin,cu);
if (fSumw2.fN) {
Double_t error1 = factor*h1->GetBinError(bin);
fSumw2.fArray[bin] += c1*c1*error1*error1;
}
}
}
}
}
//______________________________________________________________________________
void TH1::Add(const TH1 *h1, const TH1 *h2, Double_t c1, Double_t c2)
{
// -*-*-*Replace contents of this histogram by the addition of h1 and h2*-*-*
// ===============================================================
//
// this = c1*h1 + c2*h2
// if errors are defined (see TH1::Sumw2), errors are also recalculated
// Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this
// if not already set.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Add
if (!h1 || !h2) {
Error("Add","Attempt to add a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()
|| nbinsx != h2->GetNbinsX() || nbinsy != h2->GetNbinsY() || nbinsz != h2->GetNbinsZ()) {
Error("Add","Attempt to add histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Add","Attempt to add histograms with different axis limits");
}
if (fXaxis.GetXmin() != h2->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h2->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h2->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h2->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h2->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h2->fZaxis.GetXmax()) {
Warning("Add","Attempt to add histograms::Add with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 or h2 have Sumw2 set
if (fSumw2.fN == 0 && (h1->GetSumw2N() != 0 || h2->GetSumw2N() != 0)) Sumw2();
// - Add statistics
Double_t nEntries = c1*h1->GetEntries() + c2*h2->GetEntries();
Stat_t s1[kNstat], s2[kNstat], s3[kNstat];
Int_t i;
for (i=0;i<kNstat;i++) {s1[i] = s2[i] = s3[i] = 0;}
h1->GetStats(s1);
h2->GetStats(s2);
for (i=0;i<kNstat;i++) {
if (i == 1) s3[i] = c1*c1*s1[i] + c2*c2*s2[i];
else s3[i] = c1*s1[i] + c2*s2[i];
}
PutStats(s3);
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
cu = c1*h1->GetBinContent(bin)+ c2*h2->GetBinContent(bin);
SetBinContent(bin,cu);
if (fSumw2.fN) {
Double_t error1 = h1->GetBinError(bin);
Double_t error2 = h2->GetBinError(bin);
fSumw2.fArray[bin] = c1*c1*error1*error1 + c2*c2*error2*error2;
}
}
}
}
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::AddBinContent(Int_t)
{
// -*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
AbstractMethod("AddBinContent");
}
//______________________________________________________________________________
void TH1::AddBinContent(Int_t, Stat_t)
{
// -*-*-*-*-*-*-*-*Increment bin content by a weight w*-*-*-*-*-*-*-*-*-*-*
// ===================================
AbstractMethod("AddBinContent");
}
//______________________________________________________________________________
void TH1::AddDirectory(Bool_t add)
{
// Sets the flag controlling the automatic add of histograms in memory
//
// By default (fAddDirectory = kTRUE), histograms are automatically added
// to the list of objects in memory.
// Note that one histogram can be removed from its support directory
// by calling h->SetDirectory(0) or h->SetDirectory(dir) to add it
// to the list of objects in the directory dir.
//
// NOTE that this is a static function. To call it, use;
// TH1::AddDirectory
fgAddDirectory = add;
}
//______________________________________________________________________________
Int_t TH1::BufferEmpty(Int_t action)
{
// Fill histogram with all entries in the buffer.
// action = -1 histogram is reset and refilled from the buffer (called by THistPainter::Paint)
// action = 0 histogram is filled from the buffer
// action = 1 histogram is filled and buffer is deleted
// The buffer is automatically deleted when the number of entries
// in the buffer is greater than the number of entries in the histogram
// do we need to compute the bin size?
if (!fBuffer) return 0;
Int_t nbentries = (Int_t)fBuffer[0];
if (!nbentries) return 0;
Double_t *buffer = fBuffer;
if (nbentries < 0) {
if (action == 0) return 0;
nbentries = -nbentries;
fBuffer=0;
Reset();
fBuffer = buffer;
}
if (TestBit(kCanRebin) || (fXaxis.GetXmax() <= fXaxis.GetXmin())) {
//find min, max of entries in buffer
Double_t xmin = fBuffer[2];
Double_t xmax = xmin;
for (Int_t i=1;i<nbentries;i++) {
Double_t x = fBuffer[2*i+2];
if (x < xmin) xmin = x;
if (x > xmax) xmax = x;
}
if (fXaxis.GetXmax() <= fXaxis.GetXmin()) {
THLimitsFinder::GetLimitsFinder()->FindGoodLimits(this,xmin,xmax);
} else {
fBuffer = 0;
Int_t keep = fBufferSize; fBufferSize = 0;
if (xmin < fXaxis.GetXmin()) RebinAxis(xmin,"X");
if (xmax >= fXaxis.GetXmax()) RebinAxis(xmax,"X");
fBuffer = buffer;
fBufferSize = keep;
}
}
FillN(nbentries,&fBuffer[2],&fBuffer[1],2);
if (action > 0) { delete [] fBuffer; fBuffer = 0; fBufferSize = 0;}
else {
if (nbentries == (Int_t)fEntries) fBuffer[0] = -nbentries;
else fBuffer[0] = 0;
}
return nbentries;
}
//______________________________________________________________________________
Int_t TH1::BufferFill(Axis_t x, Stat_t w)
{
// accumulate arguments in buffer. When buffer is full, empty the buffer
// fBuffer[0] = number of entries in buffer
// fBuffer[1] = w of first entry
// fBuffer[2] = x of first entry
if (!fBuffer) return -2;
Int_t nbentries = (Int_t)fBuffer[0];
if (nbentries < 0) {
nbentries = -nbentries;
fBuffer[0] = nbentries;
if (fEntries > 0) {
Double_t *buffer = fBuffer; fBuffer=0;
Reset();
fBuffer = buffer;
}
}
if (2*nbentries+2 >= fBufferSize) {
BufferEmpty(1);
return Fill(x,w);
}
fBuffer[2*nbentries+1] = w;
fBuffer[2*nbentries+2] = x;
fBuffer[0] += 1;
return -2;
}
//______________________________________________________________________________
Double_t TH1::Chi2Test(const TH1 *h, Option_t *option, Int_t constraint) const
{
//The Chi2 (Pearson's) test for differences between h and this histogram.
//a small value of prob indicates a significant difference between the distributions
//
//if the data was collected in such a way that the number of entries
//in the first histogram is necessarily equal to the number of entries
//in the second, the parameter _constraint_ must be made 1. Default is 0.
//any additional constraints on the data lower the number of degrees of freedom
//(i.e. increase constraint to more positive values) in accordance with
//their number
//
///options:
// "O" : overflows included
// "U" : underflows included
// by default underflows and overflows are not included
//
// "P" : print information about number of degrees of freedom and the value of chi2
// "Chi2" : the function returns the Chisquare instead of the probability
// "Chi2/ndf" : the function returns the Chi2/ndf
// if none of the options "Chi2" or "Chi2/ndf" is specified, the function returns
// the Pearson test, ie probability.
//
// algorithm taken from "Numerical Recipes in C++"
// implementation by Anna Kreshuk
//
// A good description of the Chi2test can be seen at:
// http://www.itl.nist.gov/div898/handbook/eda/section3/eda35f.htm
// See also TH1::KolmogorovTest (including NOTE2)
Int_t i, i_start, i_end;
TString opt = option;
opt.ToUpper();
TAxis *axis1 = this->GetXaxis();
TAxis *axis2 = h->GetXaxis();
Int_t nbins1 = axis1->GetNbins();
Int_t nbins2 = axis2->GetNbins();
//check dimensions
if (this->GetDimension()!=1 || h->GetDimension()!=1){
Error("Chi2Test","for 1-d only");
return 0;
}
//check number of channels
if (nbins1 != nbins2){
Error("Chi2Test","different number of channels");
return 0;
}
//see options
i_start = 1;
i_end = nbins1;
Int_t ndf = nbins1-constraint;
if(opt.Contains("O")) {
i_end = nbins1+1;
ndf++;
}
if(opt.Contains("U")) {
i_start = 0;
ndf++;
}
//Compute the normalisation factor
Double_t sum1=0, sum2=0;
for (i=i_start; i<=i_end; i++){
sum1 += this->GetBinContent(i);
sum2 += h->GetBinContent(i);
}
//check that the histograms are not empty
if (sum1 == 0 || sum2 == 0){
Error("Chi2Test","one of the histograms is empty");
return 0;
}
Double_t chsq = 0;
Double_t bin1, bin2, err1, err2, temp;
for (i=i_start; i<=i_end; i++){
bin1 = this->GetBinContent(i)/sum1;
bin2 = h->GetBinContent(i)/sum2;
if (bin1 ==0 && bin2==0){
--ndf; //no data means one less degree of freedom
} else {
temp = bin1-bin2;
err1=this->GetBinError(i);
err2=h->GetBinError(i);
if (err1 == 0 && err2 == 0){
Error("Chi2Test", "bins with non-zero content and zero error");
return 0;
}
err1*=err1;
err2*=err2;
err1/=sum1*sum1;
err2/=sum2*sum2;
chsq+=temp*temp/(err1+err2);
}
}
Double_t prob = TMath::Prob(0.5*chsq, Int_t(0.5*ndf));
if (opt.Contains("P")){
Printf("Chi2 = %f, Prob = %g, NDF = %d\n", chsq,prob,ndf);
}
if (opt.Contains("CHI2/NDF")){
if (ndf == 0) return 0;
return chsq/ndf;
}
if (opt.Contains("CHI2")){
return chsq;
}
return prob;
}
//______________________________________________________________________________
Double_t TH1::ComputeIntegral()
{
// Compute integral (cumulative sum of bins)
// The result stored in fIntegral is used by the GetRandom functions.
// This function is automatically called by GetRandom when the fIntegral
// array does not exist or when the number of entries in the histogram
// has changed since the previous call to GetRandom.
// The resulting integral is normalized to 1
Int_t bin, binx, biny, binz, ibin;
// delete previously computed integral (if any)
if (fIntegral) delete [] fIntegral;
// - Allocate space to store the integral and compute integral
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
Int_t nxy = nbinsx*nbinsy;
Int_t nbins = nxy*nbinsz;
fIntegral = new Double_t[nbins+2];
ibin = 0;
fIntegral[ibin] = 0;
for (binz=1;binz<=nbinsz;binz++) {
for (biny=1;biny<=nbinsy;biny++) {
for (binx=1;binx<=nbinsx;binx++) {
ibin++;
bin = GetBin(binx, biny, binz);
fIntegral[ibin] = fIntegral[ibin-1] + GetBinContent(bin);
}
}
}
// - Normalize integral to 1
if (fIntegral[nbins] == 0 ) {
Error("ComputeIntegral", "Integral = zero"); return 0;
}
for (bin=1;bin<=nbins;bin++) fIntegral[bin] /= fIntegral[nbins];
fIntegral[nbins+1] = fEntries;
return fIntegral[nbins];
}
//______________________________________________________________________________
Double_t *TH1::GetIntegral()
{
// Return a pointer to the array of bins integral.
// if the pointer fIntegral is null, TH1::ComputeIntegral is called
if (fIntegral) ComputeIntegral();
return fIntegral;
}
//______________________________________________________________________________
void TH1::Copy(TObject &obj) const
{
// -*-*-*-*-*Copy this histogram structure to newth1*-*-*-*-*-*-*-*-*-*-*-*
// =======================================
//
// Note that this function does not copy the list of associated functions.
// Use TObJect::Clone to make a full copy of an histogram.
if (((TH1&)obj).fDirectory) {
// We are likely to change the hash value of this object
// with TNamed::Copy, to keep things correct, we need to
// clean up its existing entries.
((TH1&)obj).fDirectory->GetList()->Remove(&obj);
((TH1&)obj).fDirectory = 0;
}
TNamed::Copy(obj);
((TH1&)obj).fDimension = fDimension;
((TH1&)obj).fNormFactor= fNormFactor;
((TH1&)obj).fEntries = fEntries;
((TH1&)obj).fNcells = fNcells;
((TH1&)obj).fBarOffset = fBarOffset;
((TH1&)obj).fBarWidth = fBarWidth;
((TH1&)obj).fTsumw = fTsumw;
((TH1&)obj).fTsumw2 = fTsumw2;
((TH1&)obj).fTsumwx = fTsumwx;
((TH1&)obj).fTsumwx2 = fTsumwx2;
((TH1&)obj).fMaximum = fMaximum;
((TH1&)obj).fMinimum = fMinimum;
((TH1&)obj).fOption = fOption;
((TH1&)obj).fBuffer = 0;
((TH1&)obj).fBufferSize= fBufferSize;
if (fBuffer) {
Double_t *buf = new Double_t[fBufferSize];
for (Int_t i=0;i<fBufferSize;i++) buf[i] = fBuffer[i];
((TH1&)obj).fBuffer = buf;
}
TAttLine::Copy(((TH1&)obj));
TAttFill::Copy(((TH1&)obj));
TAttMarker::Copy(((TH1&)obj));
fXaxis.Copy(((TH1&)obj).fXaxis);
fYaxis.Copy(((TH1&)obj).fYaxis);
fZaxis.Copy(((TH1&)obj).fZaxis);
((TH1&)obj).fXaxis.SetParent(&obj);
((TH1&)obj).fYaxis.SetParent(&obj);
((TH1&)obj).fZaxis.SetParent(&obj);
fContour.Copy(((TH1&)obj).fContour);
fSumw2.Copy(((TH1&)obj).fSumw2);
// fFunctions->Copy(((TH1&)obj).fFunctions);
if (fgAddDirectory && gDirectory) {
gDirectory->Append(&obj);
((TH1&)obj).fDirectory = gDirectory;
}
}
//______________________________________________________________________________
Int_t TH1::DistancetoPrimitive(Int_t px, Int_t py)
{
// -*-*-*-*-*-*-*-*-*Compute distance from point px,py to a line*-*-*-*-*-*
// ===========================================
// Compute the closest distance of approach from point px,py to elements
// of an histogram.
// The distance is computed in pixels units.
//
// Algorithm:
// Currently, this simple model computes the distance from the mouse
// to the histogram contour only.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (!fPainter) return 9999;
return fPainter->DistancetoPrimitive(px,py);
}
//______________________________________________________________________________
void TH1::Divide(TF1 *f1, Double_t c1)
{
// Performs the operation: this = this/(c1*f1)
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
//
// Only bins inside the function range are recomputed.
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Divide
if (!f1) {
Error("Add","Attempt to divide by a non-existing function");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// - Add statistics
Double_t nEntries = fEntries;
Stat_t s1[10];
Int_t i;
for (i=0;i<10;i++) {s1[i] = 0;}
PutStats(s1);
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu,w;
Double_t xx[3];
Double_t *params = 0;
f1->InitArgs(xx,params);
for (binz=0;binz<=nbinsz+1;binz++) {
xx[2] = fZaxis.GetBinCenter(binz);
for (biny=0;biny<=nbinsy+1;biny++) {
xx[1] = fYaxis.GetBinCenter(biny);
for (binx=0;binx<=nbinsx+1;binx++) {
xx[0] = fXaxis.GetBinCenter(binx);
if (!f1->IsInside(xx)) continue;
TF1::RejectPoint(kFALSE);
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
Double_t error1 = GetBinError(bin);
cu = c1*f1->EvalPar(xx);
if (TF1::RejectedPoint()) continue;
if (cu) w = GetBinContent(bin)/cu;
else w = 0;
SetBinContent(bin,w);
if (fSumw2.fN) {
if (cu != 0) fSumw2.fArray[bin] = error1*error1/(cu*cu);
else fSumw2.fArray[bin] = 0;
}
}
}
}
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Divide(const TH1 *h1)
{
// -*-*-*-*-*-*-*-*-*Divide this histogram by h1*-*-*-*-*-*-*-*-*-*-*-*-*
// ===========================
//
// this = this/h1
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
// Note that if h1 has Sumw2 set, Sumw2 is automatically called for this
// if not already set.
// The resulting errors are calculated assuming uncorrelated histograms.
// See the other TH1::Divide that gives the possibility to optionaly
// compute Binomial errors.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Scale
if (!h1) {
Error("Divide","Attempt to divide by a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()) {
Error("Divide","Attempt to divide histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Divide","Attempt to divide histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 has Sumw2 set
if (fSumw2.fN == 0 && h1->GetSumw2N() != 0) Sumw2();
// - Reset statistics
Double_t nEntries = fEntries;
fEntries = fTsumw = 0;
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t c0,c1,w;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = GetBin(binx,biny,binz);
c0 = GetBinContent(bin);
c1 = h1->GetBinContent(bin);
if (c1) w = c0/c1;
else w = 0;
SetBinContent(bin,w);
fEntries++;
if (fSumw2.fN) {
Double_t e0 = GetBinError(bin);
Double_t e1 = h1->GetBinError(bin);
Double_t c12= c1*c1;
if (!c1) { fSumw2.fArray[bin] = 0; continue;}
fSumw2.fArray[bin] = (e0*e0*c1*c1 + e1*e1*c0*c0)/(c12*c12);
}
}
}
}
Stat_t s[kNstat];
GetStats(s);
PutStats(s);
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Divide(const TH1 *h1, const TH1 *h2, Double_t c1, Double_t c2, Option_t *option)
{
// -*-*-*Replace contents of this histogram by the division of h1 by h2*-*-*
// ==============================================================
//
// this = c1*h1/(c2*h2)
//
// if errors are defined (see TH1::Sumw2), errors are also recalculated
// Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this
// if not already set.
// The resulting errors are calculated assuming uncorrelated histograms.
// However, if option ="B" is specified, Binomial errors are computed.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Divide
TString opt = option;
opt.ToLower();
Bool_t binomial = kFALSE;
if (opt.Contains("b")) binomial = kTRUE;
if (!h1 || !h2) {
Error("Divide","Attempt to divide by a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()
|| nbinsx != h2->GetNbinsX() || nbinsy != h2->GetNbinsY() || nbinsz != h2->GetNbinsZ()) {
Error("Divide","Attempt to divide histograms with different number of bins");
return;
}
if (!c2) {
Error("Divide","Coefficient of dividing histogram cannot be zero");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Divide","Attempt to divide histograms with different axis limits");
}
if (fXaxis.GetXmin() != h2->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h2->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h2->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h2->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h2->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h2->fZaxis.GetXmax()) {
Warning("Divide","Attempt to divide histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 or h2 have Sumw2 set
if (fSumw2.fN == 0 && (h1->GetSumw2N() != 0 || h2->GetSumw2N() != 0)) Sumw2();
// - Reset statistics
Double_t nEntries = fEntries;
fEntries = fTsumw = 0;
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t b1,b2,w,d1,d2;
d1 = c1*c1;
d2 = c2*c2;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
b1 = h1->GetBinContent(bin);
b2 = h2->GetBinContent(bin);
if (b2) w = c1*b1/(c2*b2);
else w = 0;
SetBinContent(bin,w);
fEntries++;
if (fSumw2.fN) {
Double_t e1 = h1->GetBinError(bin);
Double_t e2 = h2->GetBinError(bin);
Double_t b22= b2*b2*d2;
if (!b2) { fSumw2.fArray[bin] = 0; continue;}
if (binomial) {
if (b1 != b2) {
//fSumw2.fArray[bin] = TMath::Abs(w*(1-w)/(c2*b2));//this is the formula in Hbook/Hoper1
fSumw2.fArray[bin] = TMath::Abs(w*(1-w)/b2);
} else {
//in case b1=b2 use a simplification of the special algorithm
//from TGraphAsymmErrors::BayesDivide calling Efficiency, etc
Double_t too_low = 0;
Double_t too_high = 1;
Double_t integral;
Double_t a = b1+1;
Double_t x;
for (Int_t loop=0; loop<20; loop++) {
x = 0.5*(too_high + too_low);
Double_t bt = TMath::Exp(TMath::LnGamma(a+1)-TMath::LnGamma(a)+a*log(x)+log(1-x));
if (x < (a+1.0)/(a+3.0)) integral = 1 - bt*TMath::BetaCf(x,a,1)/a;
else integral = bt*TMath::BetaCf(1-x,1,a);
if (integral > 0.683) too_low = x;
else too_high = x;
}
fSumw2.fArray[bin] = (1-x)*(1-x)/4;
}
} else {
fSumw2.fArray[bin] = d1*d2*(e1*e1*b2*b2 + e2*e2*b1*b1)/(b22*b22);
}
}
}
}
}
Stat_t s[kNstat];
GetStats(s);
PutStats(s);
if (nEntries == 0) nEntries = h1->GetEntries();
if (nEntries == 0) nEntries = 1;
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Draw(Option_t *option)
{
// -*-*-*-*-*-*-*-*-*Draw this histogram with options*-*-*-*-*-*-*-*-*-*-*-*
// ================================
//
// Histograms are drawn via the THistPainter class. Each histogram has
// a pointer to its own painter (to be usable in a multithreaded program).
// The same histogram can be drawn with different options in different pads.
// When an histogram drawn in a pad is deleted, the histogram is
// automatically removed from the pad or pads where it was drawn.
// If an histogram is drawn in a pad, then filled again, the new status
// of the histogram will be automatically shown in the pad next time
// the pad is updated. One does not need to redraw the histogram.
// To draw the current version of an histogram in a pad, one can use
// h->DrawCopy();
// This makes a clone of the histogram. Once the clone is drawn, the original
// histogram may be modified or deleted without affecting the aspect of the
// clone.
// By default, TH1::Draw clears the current pad.
//
// One can use TH1::SetMaximum and TH1::SetMinimum to force a particular
// value for the maximum or the minimum scale on the plot.
//
// TH1::UseCurrentStyle can be used to change all histogram graphics
// attributes to correspond to the current selected style.
// This function must be called for each histogram.
// In case one reads and draws many histograms from a file, one can force
// the histograms to inherit automatically the current graphics style
// by calling before gROOT->ForceStyle();
//
// See THistPainter::Paint for a description of all the drawing options
// =======================
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TString opt = option;
opt.ToLower();
if (gPad) {
if (!gPad->IsEditable()) (gROOT->GetMakeDefCanvas())();
if (!opt.Contains("same")) {
//the following statement is necessary in case one attempts to draw
//a temporary histogram already in the current pad
if (TestBit(kCanDelete)) gPad->GetListOfPrimitives()->Remove(this);
gPad->Clear();
}
}
AppendPad(opt.Data());
}
//______________________________________________________________________________
TH1 *TH1::DrawCopy(Option_t *) const
{
// -*-*-*-*-*Copy this histogram and Draw in the current pad*-*-*-*-*-*-*-*
// ===============================================
//
// Once the histogram is drawn into the pad, any further modification
// using graphics input will be made on the copy of the histogram,
// and not to the original object.
//
// See Draw for the list of options
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
AbstractMethod("DrawCopy");
return 0;
}
//______________________________________________________________________________
TH1 *TH1::DrawNormalized(Option_t *option, Double_t norm) const
{
// Draw a normalized copy of this histogram.
//
// A clone of this histogram is normalized to norm and drawn with option.
// A pointer to the normalized histogram is returned.
// The contents of the histogram copy are scaled such that the new
// sum of weights (excluding under and overflow) is equal to norm.
// Note that the returned normalized histogram is not added to the list
// of histograms in the current directory in memory.
// It is the user's responsability to delete this histogram.
// The kCanDelete bit is set for the returned object. If a pad containing
// this copy is cleared, the histogram will be automatically deleted.
//
// See Draw for the list of options
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Double_t sum = GetSumOfWeights();
if (sum == 0) {
Error("DrawNormalized","Sum of weights is null. Cannot normalized histogram: %s",GetName());
return 0;
}
Bool_t addStatus = TH1::AddDirectoryStatus();
TH1::AddDirectory(kFALSE);
TH1 *h = (TH1*)Clone();
h->SetBit(kCanDelete);
h->Scale(norm/sum);
h->Draw(option);
TH1::AddDirectory(addStatus);
return h;
}
//______________________________________________________________________________
void TH1::DrawPanel()
{
// -*-*-*-*-*Display a panel with all histogram drawing options*-*-*-*-*-*
// ==================================================
//
// See class TDrawPanelHist for example
if (!fPainter) {Draw(); if (gPad) gPad->Update();}
if (fPainter) fPainter->DrawPanel();
}
//______________________________________________________________________________
void TH1::Eval(TF1 *f1, Option_t *option)
{
// -*-*-*Evaluate function f1 at the center of bins of this histogram-*-*-*-*
// ============================================================
//
// If option "R" is specified, the function is evaluated only
// for the bins included in the function range.
// If option "A" is specified, the value of the function is added to the
// existing bin contents
// If option "S" is specified, the value of the function is used to
// generate a value, distributed according to the Poisson
// distribution, with f1 as the mean.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Double_t x[3];
Int_t range,stat,add,bin,binx,biny,binz,nbinsx, nbinsy, nbinsz;
if (!f1) return;
Double_t fu;
Double_t e=0;
TString opt = option;
opt.ToLower();
if (opt.Contains("a")) add = 1;
else add = 0;
if (opt.Contains("s")) stat = 1;
else stat = 0;
if (opt.Contains("r")) range = 1;
else range = 0;
nbinsx = fXaxis.GetNbins();
nbinsy = fYaxis.GetNbins();
nbinsz = fZaxis.GetNbins();
if (!add) Reset();
for (binz=1;binz<=nbinsz;binz++) {
x[2] = fZaxis.GetBinCenter(binz);
for (biny=1;biny<=nbinsy;biny++) {
x[1] = fYaxis.GetBinCenter(biny);
for (binx=1;binx<=nbinsx;binx++) {
bin = GetBin(binx,biny,binz);
x[0] = fXaxis.GetBinCenter(binx);
if (range && !f1->IsInside(x)) continue;
fu = f1->Eval(x[0],x[1],x[2]);
if (stat) fu = gRandom->PoissonD(fu);
if (fSumw2.fN) e = fSumw2.fArray[bin];
AddBinContent(bin,fu);
if (fSumw2.fN) fSumw2.fArray[bin] = e+ TMath::Abs(fu);
}
}
}
}
//______________________________________________________________________________
void TH1::ExecuteEvent(Int_t event, Int_t px, Int_t py)
{
// -*-*-*-*-*-*-*-*-*Execute action corresponding to one event*-*-*-*
// =========================================
// This member function is called when a histogram is clicked with the locator
//
// If Left button clicked on the bin top value, then the content of this bin
// is modified according to the new position of the mouse when it is released.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (fPainter) fPainter->ExecuteEvent(event, px, py);
}
//______________________________________________________________________________
Int_t TH1::Fill(Axis_t x)
{
// -*-*-*-*-*-*-*-*Increment bin with abscissa X by 1*-*-*-*-*-*-*-*-*-*-*
// ==================================
//
// if x is less than the low-edge of the first bin, the Underflow bin is incremented
// if x is greater than the upper edge of last bin, the Overflow bin is incremented
//
// If the storage of the sum of squares of weights has been triggered,
// via the function Sumw2, then the sum of the squares of weights is incremented
// by 1 in the bin corresponding to x.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (fBuffer) return BufferFill(x,1);
Int_t bin;
fEntries++;
bin =fXaxis.FindBin(x);
AddBinContent(bin);
if (fSumw2.fN) ++fSumw2.fArray[bin];
if (bin == 0 || bin > fXaxis.GetNbins()) {
if (!fgStatOverflows) return -1;
}
++fTsumw;
++fTsumw2;
fTsumwx += x;
fTsumwx2 += x*x;
return bin;
}
//______________________________________________________________________________
Int_t TH1::Fill(Axis_t x, Stat_t w)
{
// -*-*-*-*-*-*Increment bin with abscissa X with a weight w*-*-*-*-*-*-*-*
// =============================================
//
// if x is less than the low-edge of the first bin, the Underflow bin is incremented
// if x is greater than the upper edge of last bin, the Overflow bin is incremented
//
// If the storage of the sum of squares of weights has been triggered,
// via the function Sumw2, then the sum of the squares of weights is incremented
// by w^2 in the bin corresponding to x.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (fBuffer) return BufferFill(x,w);
Int_t bin;
fEntries++;
bin =fXaxis.FindBin(x);
AddBinContent(bin, w);
if (fSumw2.fN) fSumw2.fArray[bin] += w*w;
if (bin == 0 || bin > fXaxis.GetNbins()) {
if (!fgStatOverflows) return -1;
}
Stat_t z= (w > 0 ? w : -w);
fTsumw += z;
fTsumw2 += z*z;
fTsumwx += z*x;
fTsumwx2 += z*x*x;
return bin;
}
//______________________________________________________________________________
Int_t TH1::Fill(const char *namex, Stat_t w)
{
// Increment bin with namex with a weight w
//
// if x is less than the low-edge of the first bin, the Underflow bin is incremented
// if x is greater than the upper edge of last bin, the Overflow bin is incremented
//
// If the storage of the sum of squares of weights has been triggered,
// via the function Sumw2, then the sum of the squares of weights is incremented
// by w^2 in the bin corresponding to x.
//
Int_t bin;
fEntries++;
bin =fXaxis.FindBin(namex);
AddBinContent(bin, w);
if (fSumw2.fN) fSumw2.fArray[bin] += w*w;
if (bin == 0 || bin > fXaxis.GetNbins()) return -1;
Axis_t x = fXaxis.GetBinCenter(bin);
Stat_t z= (w > 0 ? w : -w);
fTsumw += z;
fTsumw2 += z*z;
fTsumwx += z*x;
fTsumwx2 += z*x*x;
return bin;
}
//______________________________________________________________________________
void TH1::FillN(Int_t ntimes, const Axis_t *x, const Double_t *w, Int_t stride)
{
// -*-*-*-*-*-*Fill this histogram with an array x and weights w*-*-*-*-*
// =================================================
//
// ntimes: number of entries in arrays x and w (array size must be ntimes*stride)
// x: array of values to be histogrammed
// w: array of weighs
// stride: step size through arrays x and w
//
// If the storage of the sum of squares of weights has been triggered,
// via the function Sumw2, then the sum of the squares of weights is incremented
// by w[i]^2 in the bin corresponding to x[i].
// if w is NULL each entry is assumed a weight=1
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t bin,i;
fEntries += ntimes;
Double_t ww = 1;
Int_t nbins = fXaxis.GetNbins();
ntimes *= stride;
for (i=0;i<ntimes;i+=stride) {
bin =fXaxis.FindBin(x[i]);
if (w) ww = w[i];
AddBinContent(bin, ww);
if (fSumw2.fN) fSumw2.fArray[bin] += ww*ww;
if (bin == 0 || bin > nbins) {
if (!fgStatOverflows) continue;
}
Stat_t z= (ww > 0 ? ww : -ww);
fTsumw += z;
fTsumw2 += z*z;
fTsumwx += z*x[i];
fTsumwx2 += z*x[i]*x[i];
}
}
//______________________________________________________________________________
void TH1::FillRandom(const char *fname, Int_t ntimes)
{
// -*-*-*-*-*Fill histogram following distribution in function fname*-*-*-*
// =======================================================
//
// The distribution contained in the function fname (TF1) is integrated
// over the channel contents.
// It is normalized to 1.
// Getting one random number implies:
// - Generating a random number between 0 and 1 (say r1)
// - Look in which bin in the normalized integral r1 corresponds to
// - Fill histogram channel
// ntimes random numbers are generated
//
// One can also call TF1::GetRandom to get a random variate from a function.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-**-*-*-*-*-*-*-*
Int_t bin, binx, ibin, loop;
Double_t r1, x, xv[1];
// - Search for fname in the list of ROOT defined functions
TF1 *f1 = (TF1*)gROOT->GetFunction(fname);
if (!f1) { Error("FillRandom", "Unknown function: %s",fname); return; }
// - Allocate temporary space to store the integral and compute integral
Int_t nbinsx = GetNbinsX();
Double_t *integral = new Double_t[nbinsx+1];
ibin = 0;
integral[ibin] = 0;
for (binx=1;binx<=nbinsx;binx++) {
xv[0] = fXaxis.GetBinCenter(binx);
ibin++;
Double_t fval = f1->Eval(xv[0]);
integral[ibin] = integral[ibin-1] + TMath::Abs(fval)*fXaxis.GetBinWidth(binx);
}
// - Normalize integral to 1
if (integral[nbinsx] == 0 ) {
Error("FillRandom", "Integral = zero"); return;
}
for (bin=1;bin<=nbinsx;bin++) integral[bin] /= integral[nbinsx];
// --------------Start main loop ntimes
for (loop=0;loop<ntimes;loop++) {
r1 = gRandom->Rndm(loop);
ibin = TMath::BinarySearch(nbinsx,&integral[0],r1);
binx = 1 + ibin;
//x = fXaxis.GetBinCenter(binx); //this is not OK when SetBuffer is used
x = fXaxis.GetBinLowEdge(ibin+1)
+fXaxis.GetBinWidth(ibin+1)*(r1-integral[ibin])/(integral[ibin+1] - integral[ibin]);
Fill(x, 1.);
}
delete [] integral;
}
//______________________________________________________________________________
void TH1::FillRandom(TH1 *h, Int_t ntimes)
{
// -*-*-*-*-*Fill histogram following distribution in histogram h*-*-*-*
// ====================================================
//
// The distribution contained in the histogram h (TH1) is integrated
// over the channel contents.
// It is normalized to 1.
// Getting one random number implies:
// - Generating a random number between 0 and 1 (say r1)
// - Look in which bin in the normalized integral r1 corresponds to
// - Fill histogram channel
// ntimes random numbers are generated
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-**-*-*-*-*-*-*-*
if (!h) { Error("FillRandom", "Null histogram"); return; }
if (fDimension != h->GetDimension()) {
Error("FillRandom", "Histograms with different dimensions"); return;
}
if (h->ComputeIntegral() == 0) return;
Int_t loop;
Axis_t x;
for (loop=0;loop<ntimes;loop++) {
x = h->GetRandom();
Fill(x);
}
}
//______________________________________________________________________________
Int_t TH1::FindBin(Axis_t x, Axis_t y, Axis_t z)
{
// -*-*-*-*Return Global bin number corresponding to x,y,z*-*-*-*-*-*-*
// ===============================================
//
// 2-D and 3-D histograms are represented with a one dimensional
// structure.
// This has the advantage that all existing functions, such as
// GetBinContent, GetBinError, GetBinFunction work for all dimensions.
// See also TH1::GetBin
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (GetDimension() < 2) {
return fXaxis.FindBin(x);
}
if (GetDimension() < 3) {
Int_t nx = fXaxis.GetNbins()+2;
Int_t binx = fXaxis.FindBin(x);
Int_t biny = fYaxis.FindBin(y);
return binx + nx*biny;
}
if (GetDimension() < 4) {
Int_t nx = fXaxis.GetNbins()+2;
Int_t ny = fYaxis.GetNbins()+2;
Int_t binx = fXaxis.FindBin(x);
Int_t biny = fYaxis.FindBin(y);
Int_t binz = fZaxis.FindBin(z);
return binx + nx*(biny +ny*binz);
}
return -1;
}
//______________________________________________________________________________
TObject *TH1::FindObject(const char *name) const
{
// search object named name in the list of functions
if (fFunctions) return fFunctions->FindObject(name);
return 0;
}
//______________________________________________________________________________
TObject *TH1::FindObject(const TObject *obj) const
{
// search object obj in the list of functions
if (fFunctions) return fFunctions->FindObject(obj);
return 0;
}
//______________________________________________________________________________
Int_t TH1::Fit(const char *fname ,Option_t *option ,Option_t *goption, Axis_t xxmin, Axis_t xxmax)
{
// Fit histogram with function fname
// =================================
// fname is the name of an already predefined function created by TF1 or TF2
// Predefined functions such as gaus, expo and poln are automatically
// created by ROOT.
// fname can also be a formula, accepted by the linear fitter (linear parts divided
// by "++" sign), for example "x++sin(x)" for fitting "[0]*x+[1]*sin(x)"
//
// This function finds a pointer to the TF1 object with name fname
// and calls TH1::Fit(TF1 *f1,...)
char *linear;
linear= (char*)strstr(fname, "++");
TF1 *f1=0;
TF2 *f2=0;
TF3 *f3=0;
Int_t ndim=GetDimension();
if (linear){
if (ndim<2){
f1=new TF1(fname, fname, xxmin, xxmax);
return Fit(f1,option,goption,xxmin,xxmax);
}
else if (ndim<3){
f2=new TF2(fname, fname);
return Fit(f2,option,goption,xxmin,xxmax);
}
else{
f3=new TF3(fname, fname);
return Fit(f3,option,goption,xxmin,xxmax);
}
}
else{
f1 = (TF1*)gROOT->GetFunction(fname);
if (!f1) { Printf("Unknown function: %s",fname); return -1; }
return Fit(f1,option,goption,xxmin,xxmax);
}
}
//______________________________________________________________________________
Int_t TH1::Fit(TF1 *f1 ,Option_t *option ,Option_t *goption, Axis_t xxmin, Axis_t xxmax)
{
// Fit histogram with function f1
// ==============================
//
// Fit this histogram with function f1.
//
// The list of fit options is given in parameter option.
// option = "W" Set all errors to 1
// = "I" Use integral of function in bin instead of value at bin center
// = "L" Use Loglikelihood method (default is chisquare method)
// = "LL" Use Loglikelihood method and bin contents are not integers)
// = "U" Use a User specified fitting algorithm (via SetFCN)
// = "Q" Quiet mode (minimum printing)
// = "V" Verbose mode (default is between Q and V)
// = "E" Perform better Errors estimation using Minos technique
// = "B" Use this option when you want to fix one or more parameters
// and the fitting function is like "gaus","expo","poln","landau".
// = "M" More. Improve fit results
// = "R" Use the Range specified in the function range
// = "N" Do not store the graphics function, do not draw
// = "0" Do not plot the result of the fit. By default the fitted function
// is drawn unless the option"N" above is specified.
// = "+" Add this new fitted function to the list of fitted functions
// (by default, any previous function is deleted)
// = "C" In case of linear fitting, don't calculate the chisquare
// (saves time)
// = "F" If fitting a polN, switch to minuit fitter
//
// When the fit is drawn (by default), the parameter goption may be used
// to specify a list of graphics options. See TH1::Draw for a complete
// list of these options.
//
// In order to use the Range option, one must first create a function
// with the expression to be fitted. For example, if your histogram
// has a defined range between -4 and 4 and you want to fit a gaussian
// only in the interval 1 to 3, you can do:
// TF1 *f1 = new TF1("f1","gaus",1,3);
// histo->Fit("f1","R");
//
// Setting initial conditions
// ==========================
// Parameters must be initialized before invoking the Fit function.
// The setting of the parameter initial values is automatic for the
// predefined functions : poln, expo, gaus, landau. One can however disable
// this automatic computation by specifying the option "B".
// Note that if a predefined function is defined with an argument,
// eg, gaus(0), expo(1), you must specify the initial values for
// the parameters.
// You can specify boundary limits for some or all parameters via
// f1->SetParLimits(p_number, parmin, parmax);
// if parmin>=parmax, the parameter is fixed
// Note that you are not forced to fix the limits for all parameters.
// For example, if you fit a function with 6 parameters, you can do:
// func->SetParameters(0,3.1,1.e-6,-8,0,100);
// func->SetParLimits(3,-10,-4);
// func->FixParameter(4,0);
// func->SetParLimits(5, 1,1);
// With this setup, parameters 0->2 can vary freely
// Parameter 3 has boundaries [-10,-4] with initial value -8
// Parameter 4 is fixed to 0
// Parameter 5 is fixed to 100.
// When the lower limit and upper limit are equal, the parameter is fixed.
// However to fix a parameter to 0, one must call the FixParameter function.
//
// Note that option "I" gives better results but is slower.
//
//
// Changing the fitting function
// =============================
// By default the fitting function H1FitChisquare is used.
// To specify a User defined fitting function, specify option "U" and
// call the following functions:
// TVirtualFitter::Fitter(myhist)->SetFCN(MyFittingFunction)
// where MyFittingFunction is of type:
// extern void MyFittingFunction(Int_t &npar, Double_t *gin, Double_t &f, Double_t *u, Int_t flag);
//
// Associated functions
// ====================
// One or more object (typically a TF1*) can be added to the list
// of functions (fFunctions) associated to each histogram.
// When TH1::Fit is invoked, the fitted function is added to this list.
// Given an histogram h, one can retrieve an associated function
// with: TF1 *myfunc = h->GetFunction("myfunc");
//
// Access to the fit results
// =========================
// If the histogram is made persistent, the list of
// associated functions is also persistent. Given a pointer (see above)
// to an associated function myfunc, one can retrieve the function/fit
// parameters with calls such as:
// Double_t chi2 = myfunc->GetChisquare();
// Double_t par0 = myfunc->GetParameter(0); //value of 1st parameter
// Double_t err0 = myfunc->GetParError(0); //error on first parameter
//
// Access to the fit covariance matrix
// ===================================
// Example1:
// TH1F h("h","test",100,-2,2);
// h.FillRandom("gaus",1000);
// h.Fit("gaus");
// Double_t matrix[3][3];
// gMinuit->mnemat(&matrix[0][0],3);
// Example2:
// TH1F h("h","test",100,-2,2);
// h.FillRandom("gaus",1000);
// h.Fit("gaus");
// TVirtualFitter *fitter = TVirtualFitter::GetFitter();
// TMatrixD matrix(npar,npar,fitter->GetCovarianceMatrix());
// Double_t errorFirstPar = fitter->GetCovarianceMatrixElement(0,0);
//
//
// Changing the maximum number of parameters
// =========================================
// By default, the fitter TMinuit is initialized with a maximum of 25 parameters.
// You can redefine this default value by calling :
// TVirtualFitter::Fitter(0,150); //to get a maximum of 150 parameters
//
// Excluding points
// ================
// Use TF1::RejectPoint inside your fitting function to exclude points
// within a certain range from the fit. Example:
// Double_t fline(Double_t *x, Double_t *par)
// {
// if (x[0] > 2.5 && x[0] < 3.5) {
// TF1::RejectPoint();
// return 0;
// }
// return par[0] + par[1]*x[0];
// }
//
// void exclude() {
// TF1 *f1 = new TF1("f1","[0] +[1]*x +gaus(2)",0,5);
// f1->SetParameters(6,-1,5,3,0.2);
// TH1F *h = new TH1F("h","background + signal",100,0,5);
// h->FillRandom("f1",2000);
// TF1 *fline = new TF1("fline",fline,0,5,2);
// fline->SetParameters(2,-1);
// h->Fit("fline","l");
// }
//
// Warning when using the option "0"
// =================================
// When selecting the option "0", the fitted function is added to
// the list of functions of the histogram, but it is not drawn.
// You can undo what you disabled in the following way:
// h.Fit("myFunction","0"); // fit, store function but do not draw
// h.Draw(); function is not drawn
// const Int_t kNotDraw = 1<<9;
// h.GetFunction("myFunction")->ResetBit(kNotDraw);
// h.Draw(); // function is visible again
//
// Access to the Fitter information during fitting
// ===============================================
// This function calls only the abstract fitter TVirtualFitter.
// The default fitter is TFitter (calls TMinuit).
// The default fitter can be set in the resource file in etc/system.rootrc
// Root.Fitter: Fumili
// A different fitter can also be set via TVirtualFitter::SetDefaultFitter.
// For example, to call the "Fumili" fitter instead of "Minuit", do
// TVirtualFitter::SetDefaultFitter("Fumili");
// During the fitting process, the objective function:
// chisquare, likelihood or any user defined algorithm
// is called (see eg in the TFitter class, the static functions
// H1FitChisquare, H1FitLikelihood).
// This objective function, in turn, calls the user theoretical function.
// This user function is a static function called from the TF1 *f1 function.
// Inside this user defined theoretical function , one can access:
// TVirtualFitter *fitter = TVirtualFitter::GetFitter(); //the current fitter
// TH1 *hist = (TH1*)fitter->GetObjectFit(); //the histogram being fitted
// TF1 +f1 = (TF1*)fitter->GetUserFunction(); //the user theoretical function
//
// By default, the fitter TMinuit is initialized with a maximum of 25 parameters.
// For fitting linear functions (containing the "++" sign" and polN functions,
// the linear fitter is initialized.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t fitResult = 0;
Int_t i, npar,nvpar,nparx;
Double_t par, we, al, bl;
Double_t eplus,eminus,eparab,globcc,amin,aminref,edm,errdef,werr;
Double_t params[100], arglist[100];
Axis_t xmin, xmax, ymin, ymax, zmin, zmax, binwidx, binwidy, binwidz;
Int_t hxfirst, hxlast, hyfirst, hylast, hzfirst, hzlast;
TF1 *fnew1;
TF2 *fnew2;
TF3 *fnew3;
// Check validity of function
if (!f1) {
Error("Fit", "function may not be null pointer");
return 0;
}
if (f1->IsZombie()) {
Error("Fit", "function is zombie");
return 0;
}
npar = f1->GetNpar();
if (npar <= 0) {
Error("Fit", "function %s has illegal number of parameters = %d", f1->GetName(), npar);
return 0;
}
// Check that function has same dimension as histogram
if (f1->GetNdim() != GetDimension()) {
Error("Fit","function %s dimension, %d, does not match histogram dimension, %d",
f1->GetName(), f1->GetNdim(), GetDimension());
return 0;
}
hxfirst = fXaxis.GetFirst();
hxlast = fXaxis.GetLast();
binwidx = fXaxis.GetBinWidth(hxlast);
xmin = fXaxis.GetBinLowEdge(hxfirst);
xmax = fXaxis.GetBinLowEdge(hxlast) +binwidx;
hyfirst = fYaxis.GetFirst();
hylast = fYaxis.GetLast();
binwidy = fYaxis.GetBinWidth(hylast);
ymin = fYaxis.GetBinLowEdge(hyfirst);
ymax = fYaxis.GetBinLowEdge(hylast) +binwidy;
hzfirst = fZaxis.GetFirst();
hzlast = fZaxis.GetLast();
binwidz = fZaxis.GetBinWidth(hzlast);
zmin = fZaxis.GetBinLowEdge(hzfirst);
zmax = fZaxis.GetBinLowEdge(hzlast) +binwidz;
// - Decode list of options into fitOption
Foption_t fitOption;
if (!FitOptionsMake(option,fitOption)) return 0;
if (xxmin != xxmax) {
f1->SetRange(xxmin,ymin,zmin,xxmax,ymax,zmax);
fitOption.Range = 1;
}
// - Check if Minuit is initialized and create special functions
Int_t special = f1->GetNumber();
Bool_t linear = f1->IsLinear();
if (special==299+npar)
linear = kTRUE;
if (fitOption.Bound || fitOption.Like || fitOption.Errors || fitOption.Gradient || fitOption.More || fitOption.User|| fitOption.Integral || fitOption.Minuit)
linear = kFALSE;
char l[] ="TLinearFitter";
Int_t strdiff = 0;
Bool_t isSet = kFALSE;
if (TVirtualFitter::GetFitter()){
//Is a fitter already set? Is it linear?
isSet=kTRUE;
strdiff = strcmp(TVirtualFitter::GetFitter()->IsA()->GetName(), l);
}
if (linear){
//
TClass *cl = gROOT->GetClass("TLinearFitter");
if (isSet && strdiff!=0) {
delete TVirtualFitter::GetFitter();
isSet=kFALSE;
}
if (!isSet) {
TVirtualFitter::SetFitter((TVirtualFitter *)cl->New());
}
} else {
if (isSet && strdiff==0){
delete TVirtualFitter::GetFitter();
isSet=kFALSE;
}
if (!isSet)
TVirtualFitter::SetFitter(0);
}
TVirtualFitter *hFitter = TVirtualFitter::Fitter(this, f1->GetNpar());
hFitter->Clear();
// - Get pointer to the function by searching in the list of functions in ROOT
gF1 = f1;
hFitter->SetUserFunc(f1);
if (xxmin != xxmax) f1->SetRange(xxmin,ymin,zmin,xxmax,ymax,zmax);
hFitter->SetFitOption(fitOption);
// - Is a Fit range specified?
Double_t fxmin, fymin, fzmin, fxmax, fymax, fzmax;
if (fitOption.Range) {
f1->GetRange(fxmin, fymin, fzmin, fxmax, fymax, fzmax);
if (fxmin > xmin) xmin = fxmin;
if (fymin > ymin) ymin = fymin;
if (fzmin > zmin) zmin = fzmin;
if (fxmax < xmax) xmax = fxmax;
if (fymax < ymax) ymax = fymax;
if (fzmax < zmax) zmax = fzmax;
hxfirst = fXaxis.FindFixBin(xmin); if (hxfirst < 1) hxfirst = 1;
hxlast = fXaxis.FindFixBin(xmax); if (hxlast > fXaxis.GetLast()) hxlast = fXaxis.GetLast();
hyfirst = fYaxis.FindFixBin(ymin); if (hyfirst < 1) hyfirst = 1;
hylast = fYaxis.FindFixBin(ymax); if (hylast > fYaxis.GetLast()) hylast = fYaxis.GetLast();
hzfirst = fZaxis.FindFixBin(zmin); if (hzfirst < 1) hzfirst = 1;
hzlast = fZaxis.FindFixBin(zmax); if (hzlast > fZaxis.GetLast()) hzlast = fZaxis.GetLast();
} else {
f1->SetRange(xmin,ymin,zmin,xmax,ymax,zmax);
}
hFitter->SetXfirst(hxfirst); hFitter->SetXlast(hxlast);
hFitter->SetYfirst(hyfirst); hFitter->SetYlast(hylast);
hFitter->SetZfirst(hzfirst); hFitter->SetZlast(hzlast);
if (linear){
hFitter->ExecuteCommand("FitHist", 0, 0);
} else {
// - If case of a predefined function, then compute initial values of parameters
if (fitOption.Bound) special = 0;
if (special == 100) H1InitGaus();
else if (special == 400) H1InitGaus();
else if (special == 200) H1InitExpo();
else if (special == 299+npar) H1InitPolynom();
// - Some initialisations
if (!fitOption.Verbose) {
arglist[0] = -1;
hFitter->ExecuteCommand("SET PRINT", arglist,1);
arglist[0] = 0;
hFitter->ExecuteCommand("SET NOW", arglist,0);
}
// - Set error criterion for chisquare or likelihood methods
// - MINUIT ErrDEF should not be set to 0.5 in case of loglikelihood fit.
// - because the FCN is already multiplied by 2 in H1FitLikelihood
// - if Hoption.User is specified, assume that the user has already set
// - his minimization function via SetFCN.
arglist[0] = TVirtualFitter::GetErrorDef();
if (fitOption.Like) {
hFitter->SetFitMethod("H1FitLikelihood");
} else {
if (!fitOption.User) hFitter->SetFitMethod("H1FitChisquare");
}
hFitter->ExecuteCommand("SET Err",arglist,1);
// - Transfer names and initial values of parameters to Minuit
Int_t nfixed = 0;
for (i=0;i<npar;i++) {
par = f1->GetParameter(i);
f1->GetParLimits(i,al,bl);
if (al*bl != 0 && al >= bl) {
al = bl = 0;
arglist[nfixed] = i+1;
nfixed++;
}
we = 0.1*TMath::Abs(bl-al);
if (we == 0) we = 0.3*TMath::Abs(par);
if (we == 0) we = binwidx;
hFitter->SetParameter(i,f1->GetParName(i),par,we,al,bl);
}
if(nfixed > 0)hFitter->ExecuteCommand("FIX",arglist,nfixed); // Otto
// - Set Gradient
if (fitOption.Gradient) {
if (fitOption.Gradient == 1) arglist[0] = 1;
else arglist[0] = 0;
hFitter->ExecuteCommand("SET GRAD",arglist,1);
}
// - Reset Print level
if (fitOption.Verbose) {
arglist[0] = 0; hFitter->ExecuteCommand("SET PRINT", arglist,1);
}
// - Compute sum of squares of errors in the bin range
Double_t ey, sumw2=0;
for (i=hxfirst;i<=hxlast;i++) {
ey = GetBinError(i);
sumw2 += ey*ey;
}
//
//
// printf("h1: sumw2=%f\n", sumw2);
//
// - Perform minimization
arglist[0] = TVirtualFitter::GetMaxIterations();
arglist[1] = sumw2*TVirtualFitter::GetPrecision();
fitResult = hFitter->ExecuteCommand("MIGRAD",arglist,2);
if (fitResult != 0) {
// Abnormal termination, MIGRAD might not have converged on a
// minimum.
if (!fitOption.Quiet) {
Warning("Fit","Abnormal termination of minimization.");
}
}
if (fitOption.More) {
hFitter->ExecuteCommand("IMPROVE",arglist,0);
}
if (fitOption.Errors) {
hFitter->ExecuteCommand("HESSE",arglist,0);
hFitter->ExecuteCommand("MINOS",arglist,0);
}
// - Get return status
char parName[50];
for (i=0;i<npar;i++) {
hFitter->GetParameter(i,parName, par,we,al,bl);
if (!fitOption.Errors) werr = we;
else {
hFitter->GetErrors(i,eplus,eminus,eparab,globcc);
if (eplus > 0 && eminus < 0) werr = 0.5*(eplus-eminus);
else werr = we;
}
params[i] = par;
f1->SetParameter(i,par);
f1->SetParError(i,werr);
}
hFitter->GetStats(aminref,edm,errdef,nvpar,nparx);
// If Log Likelihood, compute an equivalent chisquare
//if (fitOption.Like) amin = hFitter->Chisquare(npar, params, amin, params, 1);
amin = aminref;
if (fitOption.Like) amin = hFitter->Chisquare(npar, params);
f1->SetChisquare(amin);
f1->SetNDF(f1->GetNumberFitPoints()-npar+nfixed);
}
// - Print final values of parameters.
if (!fitOption.Quiet) {
if (fitOption.Errors) hFitter->PrintResults(4,aminref);
else hFitter->PrintResults(3,aminref);
}
// - Store fitted function in histogram functions list and draw
if (!fitOption.Nostore) {
if (!fitOption.Plus) {
TIter next(fFunctions, kIterBackward);
TObject *obj;
while ((obj = next())) {
if (obj->InheritsFrom(TF1::Class())) {
fFunctions->Remove(obj);
delete obj;
}
}
}
if (GetDimension() < 2) {
fnew1 = new TF1();
f1->Copy(*fnew1);
fFunctions->Add(fnew1);
fnew1->SetParent(this);
fnew1->Save(xmin,xmax,0,0,0,0);
if (fitOption.Nograph) fnew1->SetBit(TF1::kNotDraw);
fnew1->SetBit(TFormula::kNotGlobal);
} else if (GetDimension() < 3) {
fnew2 = new TF2();
f1->Copy(*fnew2);
fFunctions->Add(fnew2);
fnew2->SetParent(this);
fnew2->Save(xmin,xmax,ymin,ymax,0,0);
if (fitOption.Nograph) fnew2->SetBit(TF1::kNotDraw);
fnew2->SetBit(TFormula::kNotGlobal);
} else {
fnew3 = new TF3();
f1->Copy(*fnew3);
fFunctions->Add(fnew3);
fnew3->SetParent(this);
fnew3->SetBit(TFormula::kNotGlobal);
}
if (TestBit(kCanDelete)) return fitResult;
if (!fitOption.Nograph && GetDimension() < 3) Draw(goption);
}
return fitResult;
}
//______________________________________________________________________________
void TH1::FitPanel()
{
// -*-*-*-*-*Display a panel with all histogram fit options*-*-*-*-*-*
// ==============================================
//
// See class TFitPanel for example
if (fPainter) fPainter->FitPanel();
}
//______________________________________________________________________________
TH1 *TH1::GetAsymmetry(TH1* h2, Double_t c2, Double_t dc2)
{
// return an histogram containing the asymmetry of this histogram with h2,
// where the asymmetry is defined as:
//
// Asymmetry = (h1 - h2)/(h1 + h2) where h1 = this
//
// works for 1D, 2D, etc. histograms
// c2 is an optional argument that gives a relative weight between the two
// histograms, and dc2 is the error on this weight. This is useful, for example,
// when forming an asymmetry between two histograms from 2 different data sets that
// need to be normalized to each other in some way. The function calculates
// the errors asumming Poisson statistics on h1 and h2 (that is, dh = sqrt(h)).
//
// example: assuming 'h1' and 'h2' are already filled
//
// h3 = h1->GetAsymmetry(h2)
//
// then 'h3' is created and filled with the asymmetry between 'h1' and 'h2';
// h1 and h2 are left intact.
//
// Note that it is the user's responsibility to manage the created histogram.
//
// code proposed by Jason Seely (seely@mit.edu) and adapted by R.Brun
//
// clone the histograms so top and bottom will have the
// correct dimensions:
// Sumw2 just makes sure the errors will be computed properly
// when we form sums and ratios below.
Bool_t addStatus = TH1::AddDirectoryStatus();
TH1::AddDirectory(kFALSE);
TH1 *asym = (TH1*)Clone();
asym->Sumw2();
TH1 *top = (TH1*)asym->Clone();
TH1 *bottom = (TH1*)asym->Clone();
TH1::AddDirectory(addStatus);
// form the top and bottom of the asymmetry, and then divide:
TH1 *h1 = this;
top->Add(h1,h2,1,-c2);
bottom->Add(h1,h2,1,c2);
asym->Divide(top,bottom);
Int_t xmax = asym->GetNbinsX();
Int_t ymax = asym->GetNbinsY();
Int_t zmax = asym->GetNbinsZ();
Double_t bot, error, a, b, da, db;
// now loop over bins to calculate the correct errors
// the reason this error calculation looks complex is because of c2
for(Int_t i=1; i<= xmax; i++){
for(Int_t j=1; j<= ymax; j++){
for(Int_t k=1; k<= zmax; k++){
// here some bin contents are written into variables to make the error
// calculation a little more legible:
a = h1->GetBinContent(i,j,k);
b = h2->GetBinContent(i,j,k);
bot = bottom->GetBinContent(i,j,k);
// make sure there are some events, if not, then the errors are set = 0
// automatically.
if(bot < 1){}
else{
// computation of errors by Christos Leonidopoulos
da = h1->GetBinError(i,j,k);
db = h2->GetBinError(i,j,k);
error = 2*TMath::Sqrt(a*a*c2*c2*db*db + c2*c2*b*b*da*da+a*a*b*b*dc2*dc2)/(bot*bot);
asym->SetBinError(i,j,k,error);
}
}
}
}
delete top;
delete bottom;
return asym;
}
//______________________________________________________________________________
Int_t TH1::GetDefaultBufferSize()
{
// return the default buffer size for automatic histograms
// the parameter fgBufferSize may be changed via SetDefaultBufferSize
return fgBufferSize;
}
//______________________________________________________________________________
Double_t TH1::GetEntries() const
{
// return the current number of entries
if (fBuffer) ((TH1*)this)->BufferEmpty();
return fEntries;
}
//______________________________________________________________________________
char *TH1::GetObjectInfo(Int_t px, Int_t py) const
{
// Redefines TObject::GetObjectInfo.
// Displays the histogram info (bin number, contents, integral up to bin
// corresponding to cursor position px,py
//
return ((TH1*)this)->GetPainter()->GetObjectInfo(px,py);
}
//______________________________________________________________________________
TVirtualHistPainter *TH1::GetPainter()
{
// return pointer to painter
// if painter does not exist, it is created
if (!fPainter) fPainter = TVirtualHistPainter::HistPainter(this);
return fPainter;
}
//______________________________________________________________________________
Int_t TH1::GetQuantiles(Int_t nprobSum, Double_t *q, const Double_t *probSum)
{
// Compute Quantiles for this histogram
// Quantile x_q of a probability distribution Function F is defined as
//
// F(x_q) = q with 0 <= q <= 1.
//
// For instance the median x_0.5 of a distribution is defined as that value
// of the random variable for which the distribution function equals 0.5:
//
// F(x_0.5) = Probability(x < x_0.5) = 0.5
//
// code from Eddy Offermann, Renaissance
//
// input parameters
// - this 1-d histogram (TH1F,D,etc). Could also be a TProfile
// - nprobSum maximum size of array q and size of array probSum (if given)
// - probSum array of positions where quantiles will be computed.
// if probSum is null, probSum will be computed internally and will
// have a size = number of bins + 1 in h. it will correspond to the
// quantiles calculated at the lowest edge of the histogram (quantile=0) and
// all the upper edges of the bins.
// if probSum is not null, it is assumed to contain at least nprobSum values.
// output
// - return value nq (<=nprobSum) with the number of quantiles computed
// - array q filled with nq quantiles
//
// Note that the Integral of the histogram is automatically recomputed
// if the number of entries is different of the number of entries when
// the integral was computed last time. In case you do not use the Fill
// functions to fill your histogram, but SetBinContent, you must call
// TH1::ComputeIntegral before calling this function.
//
// Getting quantiles q from two histograms and storing results in a TGraph,
// a so-called QQ-plot
//
// TGraph *gr = new TGraph(nprob);
// h1->GetQuantiles(nprob,gr->GetX());
// h2->GetQuantiles(nprob,gr->GetY());
// gr->Draw("alp");
//
// Example:
// void quantiles() {
// // demo for quantiles
// const Int_t nq = 20;
// TH1F *h = new TH1F("h","demo quantiles",100,-3,3);
// h->FillRandom("gaus",5000);
//
// Double_t xq[nq]; // position where to compute the quantiles in [0,1]
// Double_t yq[nq]; // array to contain the quantiles
// for (Int_t i=0;i<nq;i++) xq[i] = Float_t(i+1)/nq;
// h->GetQuantiles(nq,yq,xq);
//
// //show the original histogram in the top pad
// TCanvas *c1 = new TCanvas("c1","demo quantiles",10,10,700,900);
// c1->Divide(1,2);
// c1->cd(1);
// h->Draw();
//
// // show the quantiles in the bottom pad
// c1->cd(2);
// gPad->SetGrid();
// TGraph *gr = new TGraph(nq,xq,yq);
// gr->SetMarkerStyle(21);
// gr->Draw("alp");
// }
if (GetDimension() > 1) {
Error("GetQuantiles","Only available for 1-d histograms");
return 0;
}
const Int_t nbins = GetXaxis()->GetNbins();
if (!fIntegral) ComputeIntegral();
if (fIntegral && fIntegral[nbins+1] != fEntries) ComputeIntegral();
Int_t i, ibin;
Double_t *prob = (Double_t*)probSum;
Int_t nq = nprobSum;
if (probSum == 0) {
nq = nbins+1;
prob = new Double_t[nq];
prob[0] = 0;
for (i=1;i<nq;i++) {
prob[i] = fIntegral[i]/fIntegral[nbins];
}
}
for (i = 0; i < nq; i++) {
ibin = TMath::BinarySearch(nbins,fIntegral,prob[i]);
while (ibin < nbins-1 && fIntegral[ibin+1] == prob[i]) {
if (fIntegral[ibin+2] == prob[i]) ibin++;
else break;
}
q[i] = GetBinLowEdge(ibin+1);
const Double_t dint = fIntegral[ibin+1]-fIntegral[ibin];
if (dint > 0) q[i] += GetBinWidth(ibin+1)*(prob[i]-fIntegral[ibin])/dint;
}
if (!probSum) delete [] prob;
return nq;
}
//______________________________________________________________________________
Int_t TH1::FitOptionsMake(Option_t *choptin, Foption_t &fitOption)
{
// -*-*-*-*-*-*-*Decode string choptin and fill fitOption structure*-*-*-*-*-*
// ================================================
Int_t nch = strlen(choptin);
if (!nch) return 1;
char chopt[32];
strcpy(chopt,choptin);
for (Int_t i=0;i<nch;i++) chopt[i] = toupper(choptin[i]);
if (strstr(chopt,"Q")) fitOption.Quiet = 1;
if (strstr(chopt,"V")) {fitOption.Verbose = 1; fitOption.Quiet = 0;}
if (strstr(chopt,"L")) fitOption.Like = 1;
if (strstr(chopt,"LL")) fitOption.Like = 2;
if (strstr(chopt,"W")) fitOption.W1 = 1;
if (strstr(chopt,"E")) fitOption.Errors = 1;
if (strstr(chopt,"M")) fitOption.More = 1;
if (strstr(chopt,"R")) fitOption.Range = 1;
if (strstr(chopt,"G")) fitOption.Gradient= 1;
if (strstr(chopt,"N")) fitOption.Nostore = 1;
if (strstr(chopt,"0")) fitOption.Nograph = 1;
if (strstr(chopt,"+")) fitOption.Plus = 1;
if (strstr(chopt,"I")) fitOption.Integral= 1;
if (strstr(chopt,"B")) fitOption.Bound = 1;
if (strstr(chopt,"U")) {fitOption.User = 1; fitOption.Like = 0;}
if (strstr(chopt,"F")) fitOption.Minuit = 1;
if (strstr(chopt,"C")) fitOption.Nochisq = 1;
return 1;
}
//______________________________________________________________________________
void H1InitGaus()
{
// -*-*-*-*Compute Initial values of parameters for a gaussian*-*-*-*-*-*-*
// ===================================================
Double_t allcha, sumx, sumx2, x, val, rms, mean;
Int_t bin;
const Double_t sqrtpi = 2.506628;
// - Compute mean value and RMS of the histogram in the given range
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
TH1 *curHist = (TH1*)hFitter->GetObjectFit();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
Double_t valmax = curHist->GetBinContent(hxfirst);
Double_t binwidx = curHist->GetBinWidth(hxfirst);
allcha = sumx = sumx2 = 0;
for (bin=hxfirst;bin<=hxlast;bin++) {
x = curHist->GetBinCenter(bin);
val = TMath::Abs(curHist->GetBinContent(bin));
if (val > valmax) valmax = val;
sumx += val*x;
sumx2 += val*x*x;
allcha += val;
}
if (allcha == 0) return;
mean = sumx/allcha;
rms = TMath::Sqrt(sumx2/allcha - mean*mean);
if (rms == 0) rms = binwidx*(hxlast-hxfirst+1)/4;
//if the distribution is really gaussian, the best approximation
//is binwidx*allcha/(sqrtpi*rms)
//However, in case of non-gaussian tails, this underestimates
//the normalisation constant. In this case the maximum value
//is a better approximation.
//We take the average of both quantities
Double_t constant = 0.5*(valmax+binwidx*allcha/(sqrtpi*rms));
//In case the mean value is outside the histo limits and
//the RMS is bigger than the range, we take
// mean = center of bins
// rms = half range
Axis_t xmin = curHist->GetXaxis()->GetXmin();
Axis_t xmax = curHist->GetXaxis()->GetXmax();
if ((mean < xmin || mean > xmax) && rms > (xmax-xmin)) {
mean = 0.5*(xmax+xmin);
rms = 0.5*(xmax-xmin);
}
TF1 *f1 = (TF1*)hFitter->GetUserFunc();
f1->SetParameter(0,constant);
f1->SetParameter(1,mean);
f1->SetParameter(2,rms);
f1->SetParLimits(2,0,10*rms);
}
//______________________________________________________________________________
void H1InitExpo()
{
// -*-*-*-*Compute Initial values of parameters for an exponential*-*-*-*-*
// =======================================================
Double_t constant, slope;
Int_t ifail;
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
Int_t nchanx = hxlast - hxfirst + 1;
H1LeastSquareLinearFit(-nchanx, constant, slope, ifail);
TF1 *f1 = (TF1*)hFitter->GetUserFunc();
f1->SetParameter(0,constant);
f1->SetParameter(1,slope);
}
//______________________________________________________________________________
void H1InitPolynom()
{
// -*-*-*-*Compute Initial values of parameters for a polynom*-*-*-*-*-*-*
// ===================================================
Double_t fitpar[25];
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
TF1 *f1 = (TF1*)hFitter->GetUserFunc();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
Int_t nchanx = hxlast - hxfirst + 1;
Int_t npar = f1->GetNpar();
if (nchanx <=1 || npar == 1) {
TH1 *curHist = (TH1*)hFitter->GetObjectFit();
fitpar[0] = curHist->GetSumOfWeights()/Double_t(nchanx);
} else {
H1LeastSquareFit( nchanx, npar, fitpar);
}
for (Int_t i=0;i<npar;i++) f1->SetParameter(i, fitpar[i]);
}
//______________________________________________________________________________
void H1LeastSquareFit(Int_t n, Int_t m, Double_t *a)
{
// -*-*-*-*-*-*Least squares lpolynomial fitting without weights*-*-*-*-*-*-*
// =================================================
//
// n number of points to fit
// m number of parameters
// a array of parameters
//
// based on CERNLIB routine LSQ: Translated to C++ by Rene Brun
// (E.Keil. revised by B.Schorr, 23.10.1981.)
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
const Double_t zero = 0.;
const Double_t one = 1.;
const Int_t idim = 20;
Double_t b[400] /* was [20][20] */;
Int_t i, k, l, ifail;
Double_t power;
Double_t da[20], xk, yk;
if (m <= 2) {
H1LeastSquareLinearFit(n, a[0], a[1], ifail);
return;
}
if (m > idim || m > n) return;
b[0] = Double_t(n);
da[0] = zero;
for (l = 2; l <= m; ++l) {
b[l-1] = zero;
b[m + l*20 - 21] = zero;
da[l-1] = zero;
}
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
TH1 *curHist = (TH1*)hFitter->GetObjectFit();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
for (k = hxfirst; k <= hxlast; ++k) {
xk = curHist->GetBinCenter(k);
yk = curHist->GetBinContent(k);
power = one;
da[0] += yk;
for (l = 2; l <= m; ++l) {
power *= xk;
b[l-1] += power;
da[l-1] += power*yk;
}
for (l = 2; l <= m; ++l) {
power *= xk;
b[m + l*20 - 21] += power;
}
}
for (i = 3; i <= m; ++i) {
for (k = i; k <= m; ++k) {
b[k - 1 + (i-1)*20 - 21] = b[k + (i-2)*20 - 21];
}
}
H1LeastSquareSeqnd(m, b, idim, ifail, 1, da);
for (i=0; i<m; ++i) a[i] = da[i];
}
//______________________________________________________________________________
void H1LeastSquareLinearFit(Int_t ndata, Double_t &a0, Double_t &a1, Int_t &ifail)
{
// -*-*-*-*-*-*-*-*Least square linear fit without weights*-*-*-*-*-*-*-*-*
// =======================================
//
// extracted from CERNLIB LLSQ: Translated to C++ by Rene Brun
// (added to LSQ by B. Schorr, 15.02.1982.)
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Double_t xbar, ybar, x2bar;
Int_t i, n;
Double_t xybar;
Double_t fn, xk, yk;
Double_t det;
n = TMath::Abs(ndata);
ifail = -2;
xbar = ybar = x2bar = xybar = 0;
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
TH1 *curHist = (TH1*)hFitter->GetObjectFit();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
for (i = hxfirst; i <= hxlast; ++i) {
xk = curHist->GetBinCenter(i);
yk = curHist->GetBinContent(i);
if (ndata < 0) {
if (yk <= 0) yk = 1e-9;
yk = TMath::Log(yk);
}
xbar += xk;
ybar += yk;
x2bar += xk*xk;
xybar += xk*yk;
}
fn = Double_t(n);
det = fn*x2bar - xbar*xbar;
ifail = -1;
if (det <= 0) {
a0 = ybar/fn;
a1 = 0;
return;
}
ifail = 0;
a0 = (x2bar*ybar - xbar*xybar) / det;
a1 = (fn*xybar - xbar*ybar) / det;
}
//______________________________________________________________________________
void H1LeastSquareSeqnd(Int_t n, Double_t *a, Int_t idim, Int_t &ifail, Int_t k, Double_t *b)
{
// -*-*-*-*-*-*Extracted from CERN Program library routine DSEQN*-*-*-*-*-*
// =================================================
//
// : Translated to C++ by Rene Brun
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t a_dim1, a_offset, b_dim1, b_offset;
Int_t nmjp1, i, j, l;
Int_t im1, jp1, nm1, nmi;
Double_t s1, s21, s22;
const Double_t one = 1.;
/* Parameter adjustments */
b_dim1 = idim;
b_offset = b_dim1 + 1;
b -= b_offset;
a_dim1 = idim;
a_offset = a_dim1 + 1;
a -= a_offset;
if (idim < n) return;
ifail = 0;
for (j = 1; j <= n; ++j) {
if (a[j + j*a_dim1] <= 0) { ifail = -1; return; }
a[j + j*a_dim1] = one / a[j + j*a_dim1];
if (j == n) continue;
jp1 = j + 1;
for (l = jp1; l <= n; ++l) {
a[j + l*a_dim1] = a[j + j*a_dim1] * a[l + j*a_dim1];
s1 = -a[l + (j+1)*a_dim1];
for (i = 1; i <= j; ++i) { s1 = a[l + i*a_dim1] * a[i + (j+1)*a_dim1] + s1; }
a[l + (j+1)*a_dim1] = -s1;
}
}
if (k <= 0) return;
for (l = 1; l <= k; ++l) {
b[l*b_dim1 + 1] = a[a_dim1 + 1]*b[l*b_dim1 + 1];
}
if (n == 1) return;
for (l = 1; l <= k; ++l) {
for (i = 2; i <= n; ++i) {
im1 = i - 1;
s21 = -b[i + l*b_dim1];
for (j = 1; j <= im1; ++j) {
s21 = a[i + j*a_dim1]*b[j + l*b_dim1] + s21;
}
b[i + l*b_dim1] = -a[i + i*a_dim1]*s21;
}
nm1 = n - 1;
for (i = 1; i <= nm1; ++i) {
nmi = n - i;
s22 = -b[nmi + l*b_dim1];
for (j = 1; j <= i; ++j) {
nmjp1 = n - j + 1;
s22 = a[nmi + nmjp1*a_dim1]*b[nmjp1 + l*b_dim1] + s22;
}
b[nmi + l*b_dim1] = -s22;
}
}
}
//______________________________________________________________________________
Int_t TH1::GetBin(Int_t binx, Int_t biny, Int_t binz) const
{
// -*-*-*-*Return Global bin number corresponding to binx,y,z*-*-*-*-*-*-*
// ==================================================
//
// 2-D and 3-D histograms are represented with a one dimensional
// structure.
// This has the advantage that all existing functions, such as
// GetBinContent, GetBinError, GetBinFunction work for all dimensions.
//
// In case of a TH1x, returns binx directly.
//
// Convention for numbering bins
// =============================
// For all histogram types: nbins, xlow, xup
// bin = 0; underflow bin
// bin = 1; first bin with low-edge xlow INCLUDED
// bin = nbins; last bin with upper-edge xup EXCLUDED
// bin = nbins+1; overflow bin
// In case of 2-D or 3-D histograms, a "global bin" number is defined.
// For example, assuming a 3-D histogram with binx,biny,binz, the function
// Int_t bin = h->GetBin(binx,biny,binz);
// returns a global/linearized bin number. This global bin is useful
// to access the bin information independently of the dimension.
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t nx, ny, nz;
if (GetDimension() < 2) {
nx = fXaxis.GetNbins()+2;
if (binx < 0) binx = 0;
if (binx >= nx) binx = nx-1;
return binx;
}
if (GetDimension() < 3) {
nx = fXaxis.GetNbins()+2;
if (binx < 0) binx = 0;
if (binx >= nx) binx = nx-1;
ny = fYaxis.GetNbins()+2;
if (biny < 0) biny = 0;
if (biny >= ny) biny = ny-1;
return binx + nx*biny;
}
if (GetDimension() < 4) {
nx = fXaxis.GetNbins()+2;
if (binx < 0) binx = 0;
if (binx >= nx) binx = nx-1;
ny = fYaxis.GetNbins()+2;
if (biny < 0) biny = 0;
if (biny >= ny) biny = ny-1;
nz = fZaxis.GetNbins()+2;
if (binz < 0) binz = 0;
if (binz >= nz) binz = nz-1;
return binx + nx*(biny +ny*binz);
}
return -1;
}
//______________________________________________________________________________
Axis_t TH1::GetRandom() const
{
// return a random number distributed according the histogram bin contents.
// This function checks if the bins integral exists. If not, the integral
// is evaluated, normalized to one.
// The integral is automatically recomputed if the number of entries
// is not the same then when the integral was computed.
// NB Only valid for 1-d histograms. Use GetRandom2 or 3 otherwise.
if (fDimension > 1) {
Error("GetRandom","Function only valid for 1-d histograms");
return 0;
}
Int_t nbinsx = GetNbinsX();
Double_t integral;
if (fIntegral) {
if (fIntegral[nbinsx+1] != fEntries) integral = ((TH1*)this)->ComputeIntegral();
} else {
integral = ((TH1*)this)->ComputeIntegral();
if (integral == 0 || fIntegral == 0) return 0;
}
Double_t r1 = gRandom->Rndm();
Int_t ibin = TMath::BinarySearch(nbinsx,fIntegral,r1);
return GetBinLowEdge(ibin+1)
+GetBinWidth(ibin+1)*(r1-fIntegral[ibin])/(fIntegral[ibin+1] - fIntegral[ibin]);
}
//______________________________________________________________________________
Stat_t TH1::GetBinContent(Int_t) const
{
// -*-*-*-*-*Return content of bin number bin
// ================================
// Implemented in TH1C,S,F,D
//
// Convention for numbering bins
// =============================
// For all histogram types: nbins, xlow, xup
// bin = 0; underflow bin
// bin = 1; first bin with low-edge xlow INCLUDED
// bin = nbins; last bin with upper-edge xup EXCLUDED
// bin = nbins+1; overflow bin
// In case of 2-D or 3-D histograms, a "global bin" number is defined.
// For example, assuming a 3-D histogram with binx,biny,binz, the function
// Int_t bin = h->GetBin(binx,biny,binz);
// returns a global/linearized bin number. This global bin is useful
// to access the bin information independently of the dimension.
AbstractMethod("GetBinContent");
return 0;
}
//______________________________________________________________________________
Stat_t TH1::GetBinContent(Int_t binx, Int_t biny) const
{
// -*-*-*-*-*Return content of bin number binx, biny
// =======================================
// NB: Function to be called for 2-d histograms only
// see convention for numbering bins in TH1::GetBin
Int_t bin = GetBin(binx,biny);
return GetBinContent(bin);
}
//______________________________________________________________________________
Stat_t TH1::GetBinContent(Int_t binx, Int_t biny, Int_t binz) const
{
// -*-*-*-*-*Return content of bin number binx,biny,binz
// ===========================================
// NB: Function to be called for 3-d histograms only
// see convention for numbering bins in TH1::GetBin
Int_t bin = GetBin(binx,biny,binz);
return GetBinContent(bin);
}
//______________________________________________________________________________
TAxis *TH1::GetXaxis() const
{
// return a pointer to the X axis object
return &((TH1*)this)->fXaxis;
}
//______________________________________________________________________________
TAxis *TH1::GetYaxis() const
{
// return a pointer to the Y axis object
return &((TH1*)this)->fYaxis;
}
//______________________________________________________________________________
TAxis *TH1::GetZaxis() const
{
// return a pointer to the Z axis object
return &((TH1*)this)->fZaxis;
}
//___________________________________________________________________________
void TH1::LabelsDeflate(Option_t *ax)
{
// Reduce the number of bins for this axis to the number of bins having a label.
Int_t iaxis = AxisChoice(ax);
TAxis *axis = 0;
if (iaxis == 1) axis = GetXaxis();
if (iaxis == 2) axis = GetYaxis();
if (iaxis == 3) axis = GetZaxis();
if (!axis) return;
if (!axis->GetLabels()) return;
TIter next(axis->GetLabels());
TObject *obj;
Int_t nbins = 0;
while ((obj = next())) {
if (obj->GetUniqueID()) nbins++;
}
if (nbins < 1) nbins = 1;
TH1 *hold = (TH1*)Clone();
hold->SetDirectory(0);
Bool_t timedisp = axis->GetTimeDisplay();
Double_t xmin = axis->GetXmin();
Double_t xmax = axis->GetBinUpEdge(nbins);
if (xmax <= xmin) xmax = xmin +nbins;
axis->SetRange(0,0);
axis->Set(nbins,xmin,xmax);
//Int_t nbinsx = fXaxis.GetNbins();
//Int_t nbinsy = fYaxis.GetNbins();
//Int_t nbinsz = fZaxis.GetNbins();
Int_t nbinsx = hold->GetXaxis()->GetNbins();
Int_t nbinsy = hold->GetYaxis()->GetNbins();
Int_t nbinsz = hold->GetZaxis()->GetNbins();
Int_t ncells = nbinsx+2;
if (GetDimension() > 1) ncells *= nbinsy+2;
if (GetDimension() > 2) ncells *= nbinsz+2;
SetBinsLength(ncells);
Int_t errors = fSumw2.fN;
if (errors) fSumw2.Set(ncells);
axis->SetTimeDisplay(timedisp);
//now loop on all bins and refill
Double_t err,cu;
Int_t bin,ibin,binx,biny,binz;
Double_t oldEntries = fEntries;
for (binz=1;binz<=nbinsz;binz++) {
for (biny=1;biny<=nbinsy;biny++) {
for (binx=1;binx<=nbinsx;binx++) {
bin = hold->GetBin(binx,biny,binz);
ibin= GetBin(binx,biny,binz);
cu = hold->GetBinContent(bin);
SetBinContent(ibin,cu);
if (errors) {
err = hold->GetBinError(bin);
SetBinError(ibin,err);
}
}
}
}
fEntries = oldEntries;
delete hold;
}
//______________________________________________________________________________
void TH1::LabelsInflate(Option_t *ax)
{
// Double the number of bins for axis.
// Refill histogram
// This function is called by TAxis::FindBin(const char *label)
Int_t iaxis = AxisChoice(ax);
TAxis *axis = 0;
if (iaxis == 1) axis = GetXaxis();
if (iaxis == 2) axis = GetYaxis();
if (iaxis == 3) axis = GetZaxis();
if (!axis) return;
TH1 *hold = (TH1*)Clone();
hold->SetDirectory(0);
Bool_t timedisp = axis->GetTimeDisplay();
Int_t nbxold = fXaxis.GetNbins();
Int_t nbyold = fYaxis.GetNbins();
Int_t nbzold = fZaxis.GetNbins();
Int_t nbins = axis->GetNbins();
Double_t xmin = axis->GetXmin();
Double_t xmax = axis->GetXmax();
xmax = xmin + 2*(xmax-xmin);
axis->SetRange(0,0);
axis->Set(2*nbins,xmin,xmax);
Int_t nbinsx = fXaxis.GetNbins();
Int_t nbinsy = fYaxis.GetNbins();
Int_t nbinsz = fZaxis.GetNbins();
Int_t ncells = nbinsx+2;
if (GetDimension() > 1) ncells *= nbinsy+2;
if (GetDimension() > 2) ncells *= nbinsz+2;
SetBinsLength(ncells);
Int_t errors = fSumw2.fN;
if (errors) fSumw2.Set(ncells);
axis->SetTimeDisplay(timedisp);
//now loop on all bins and refill
Double_t err,cu;
Int_t bin,ibin,binx,biny,binz;
for (binz=1;binz<=nbinsz;binz++) {
for (biny=1;biny<=nbinsy;biny++) {
for (binx=1;binx<=nbinsx;binx++) {
bin = hold->GetBin(binx,biny,binz);
ibin= GetBin(binx,biny,binz);
if (binx > nbxold || biny > nbyold || binz > nbzold) bin = -1;
if (bin > 0) cu = hold->GetBinContent(bin);
else cu = 0;
SetBinContent(ibin,cu);
if (errors) {
if (bin > 0) err = hold->GetBinError(bin);
else err = 0;
SetBinError(ibin,err);
}
}
}
}
delete hold;
}
//______________________________________________________________________________
void TH1::LabelsOption(Option_t *option, Option_t *ax)
{
// Set option(s) to draw axis with labels
// option = "a" sort by alphabetic order
// = ">" sort by decreasing values
// = "<" sort by increasing values
// = "h" draw labels horizonthal
// = "v" draw labels vertical
// = "u" draw labels up (end of label right adjusted)
// = "d" draw labels down (start of label left adjusted)
Int_t iaxis = AxisChoice(ax);
TAxis *axis = 0;
if (iaxis == 1) axis = GetXaxis();
if (iaxis == 2) axis = GetYaxis();
if (iaxis == 3) axis = GetZaxis();
if (!axis) return;
THashList *labels = axis->GetLabels();
if (!labels) {
Warning("LabelsOption","Cannot sort. No labels");
return;
}
TString opt = option;
opt.ToLower();
if (opt.Contains("h")) {
axis->SetBit(TAxis::kLabelsHori);
axis->ResetBit(TAxis::kLabelsVert);
axis->ResetBit(TAxis::kLabelsDown);
axis->ResetBit(TAxis::kLabelsUp);
}
if (opt.Contains("v")) {
axis->SetBit(TAxis::kLabelsVert);
axis->ResetBit(TAxis::kLabelsHori);
axis->ResetBit(TAxis::kLabelsDown);
axis->ResetBit(TAxis::kLabelsUp);
}
if (opt.Contains("u")) {
axis->SetBit(TAxis::kLabelsUp);
axis->ResetBit(TAxis::kLabelsVert);
axis->ResetBit(TAxis::kLabelsDown);
axis->ResetBit(TAxis::kLabelsHori);
}
if (opt.Contains("d")) {
axis->SetBit(TAxis::kLabelsDown);
axis->ResetBit(TAxis::kLabelsVert);
axis->ResetBit(TAxis::kLabelsHori);
axis->ResetBit(TAxis::kLabelsUp);
}
Int_t sort = -1;
if (opt.Contains("a")) sort = 0;
if (opt.Contains(">")) sort = 1;
if (opt.Contains("<")) sort = 2;
if (sort < 0) return;
if (sort > 0 && GetDimension() > 2) {
Error("LabelsOption","Sorting by value not implemented for 3-D histograms");
return;
}
Int_t n = TMath::Min(axis->GetNbins(), labels->GetSize());
Int_t *a = new Int_t[n+2];
Int_t i,j,k;
Double_t *cont = 0;
Double_t *errors = 0;
THashList *labold = new THashList(labels->GetSize(),1);
TIter nextold(labels);
TObject *obj;
while ((obj=nextold())) {
labold->Add(obj);
}
labels->Clear();
if (sort > 0) {
//---sort by values of bins
if (GetDimension() == 1) {
cont = new Double_t[n];
if (fSumw2.fN) errors = new Double_t[n];
for (i=1;i<=n;i++) {
cont[i-1] = GetBinContent(i);
if (errors) errors[i-1] = GetBinError(i);
}
if (sort ==1) TMath::Sort(n,cont,a,kTRUE); //sort by decreasing values
else TMath::Sort(n,cont,a,kFALSE); //sort by increasing values
for (i=1;i<=n;i++) {
SetBinContent(i,cont[a[i-1]]);
if (errors) SetBinError(i,errors[a[i-1]]);
}
for (i=1;i<=n;i++) {
obj = labold->At(a[i-1]);
labels->Add(obj);
obj->SetUniqueID(i);
}
} else if (GetDimension()== 2) {
Double_t *pcont = new Double_t[n+2];
for (i=0;i<=n;i++) pcont[i] = 0;
Int_t nx = fXaxis.GetNbins();
Int_t ny = fYaxis.GetNbins();
cont = new Double_t[(nx+2)*(ny+2)];
if (fSumw2.fN) errors = new Double_t[n];
for (i=1;i<=nx;i++) {
for (j=1;j<=ny;j++) {
cont[i+nx*j] = GetBinContent(i,j);
if (errors) errors[i+nx*j] = GetBinError(i,j);
if (axis == GetXaxis()) k = i;
else k = j;
pcont[k-1] += cont[i+nx*j];
}
}
if (sort ==1) TMath::Sort(n,pcont,a,kTRUE); //sort by decreasing values
else TMath::Sort(n,pcont,a,kFALSE); //sort by increasing values
for (i=0;i<n;i++) {
obj = labold->At(a[i]);
labels->Add(obj);
obj->SetUniqueID(i+1);
}
delete [] pcont;
for (i=1;i<=nx;i++) {
for (j=1;j<=ny;j++) {
if (axis == GetXaxis()) {
SetBinContent(i,j,cont[a[i-1]+1+nx*j]);
if (errors) SetBinError(i,j,errors[a[i-1]+1+nx*j]);
} else {
SetBinContent(i,j,cont[i+nx*(a[j-1]+1)]);
if (errors) SetBinError(i,j,errors[i+nx*(a[j-1]+1)]);
}
}
}
} else {
//to be implemented
}
} else {
//---alphabetic sort
const UInt_t kUsed = 1<<18;
TObject *objk=0;
a[0] = 0;
a[n+1] = n+1;
for (i=1;i<=n;i++) {
const char *label = "zzzzzzzzzzzz";
for (j=1;j<=n;j++) {
obj = labold->At(j-1);
if (!obj) continue;
if (obj->TestBit(kUsed)) continue;
//use strcasecmp for case non-sensitive sort (may be an option)
if (strcmp(label,obj->GetName()) < 0) continue;
objk = obj;
a[i] = j;
label = obj->GetName();
}
if (objk) {
objk->SetUniqueID(i);
labels->Add(objk);
objk->SetBit(kUsed);
}
}
for (i=1;i<=n;i++) {
obj = labels->At(i-1);
if (!obj) continue;
obj->ResetBit(kUsed);
}
if (GetDimension() == 1) {
cont = new Double_t[n+2];
if (fSumw2.fN) errors = new Double_t[n+2];
for (i=1;i<=n;i++) {
cont[i] = GetBinContent(a[i]);
if (errors) errors[i] = GetBinError(a[i]);
}
for (i=1;i<=n;i++) {
SetBinContent(i,cont[i]);
if (errors) SetBinError(i,errors[i]);
}
} else if (GetDimension()== 2) {
Int_t nx = fXaxis.GetNbins()+2;
Int_t ny = fYaxis.GetNbins()+2;
cont = new Double_t[nx*ny];
if (fSumw2.fN) errors = new Double_t[nx*ny];
for (i=0;i<nx;i++) {
for (j=0;j<ny;j++) {
cont[i+nx*j] = GetBinContent(i,j);
if (errors) errors[i+nx*j] = GetBinError(i,j);
}
}
for (i=0;i<nx;i++) {
for (j=0;j<ny;j++) {
if (axis == GetXaxis()) {
SetBinContent(i,j,cont[a[i]+nx*j]);
if (errors) SetBinError(i,j,errors[a[i]+nx*j]);
} else {
SetBinContent(i,j,cont[i+nx*a[j]]);
if (errors) SetBinError(i,j,errors[i+nx*a[j]]);
}
}
}
} else {
Int_t nx = fXaxis.GetNbins()+2;
Int_t ny = fYaxis.GetNbins()+2;
Int_t nz = fZaxis.GetNbins()+2;
cont = new Double_t[nx*ny*nz];
if (fSumw2.fN) errors = new Double_t[nx*ny*nz];
for (i=0;i<nx;i++) {
for (j=0;j<ny;j++) {
for (k=0;k<nz;k++) {
cont[i+nx*(j+ny*k)] = GetBinContent(i,j,k);
if (errors) errors[i+nx*(j+ny*k)] = GetBinError(i,j,k);
}
}
}
for (i=0;i<nx;i++) {
for (j=0;j<ny;j++) {
for (k=0;k<nz;k++) {
if (axis == GetXaxis()) {
SetBinContent(i,j,k,cont[a[i]+nx*(j+ny*k)]);
if (errors) SetBinError(i,j,k,errors[a[i]+nx*(j+ny*k)]);
} else if (axis == GetYaxis()) {
SetBinContent(i,j,k,cont[i+nx*(a[j]+ny*k)]);
if (errors) SetBinError(i,j,k,errors[i+nx*(a[j]+ny*k)]);
} else {
SetBinContent(i,j,k,cont[i+nx*(j+ny*a[k])]);
if (errors) SetBinError(i,j,k,errors[i+nx*(j+ny*a[k])]);
}
}
}
}
}
}
delete labold;
if (a) delete [] a;
if (cont) delete [] cont;
if (errors) delete [] errors;
}
//______________________________________________________________________________
static Bool_t AlmostEqual(Double_t a, Double_t b, Double_t epsilon = 0.00000001)
{
return TMath::Abs(a - b) < epsilon;
}
//______________________________________________________________________________
static Bool_t AlmostInteger(Double_t a, Double_t epsilon = 0.00000001)
{
return AlmostEqual(a - TMath::Floor(a), 0, epsilon) ||
AlmostEqual(a - TMath::Floor(a), 1, epsilon);
}
//______________________________________________________________________________
Bool_t TH1::SameLimitsAndNBins(const TAxis& axis1, const TAxis& axis2)
{
if ((axis1.GetNbins() == axis2.GetNbins())
&& (axis1.GetXmin() == axis2.GetXmin())
&& (axis1.GetXmax() == axis2.GetXmax()))
return kTRUE;
else
return kFALSE;
}
//______________________________________________________________________________
Bool_t TH1::RecomputeAxisLimits(TAxis& destAxis, const TAxis& anAxis)
{
// Finds new limits for the axis for the Merge function.
// returns false if the limits are incompatible
if (SameLimitsAndNBins(destAxis, anAxis))
return kTRUE;
if (destAxis.GetXbins()->fN || anAxis.GetXbins()->fN)
return kFALSE; // user binning not supported
Axis_t width1 = destAxis.GetBinWidth(0);
Axis_t width2 = anAxis.GetBinWidth(0);
if (width1 == 0 || width2 == 0)
return kFALSE; // no binning not supported
Axis_t xmin = TMath::Min(destAxis.GetXmin(), anAxis.GetXmin());
Axis_t xmax = TMath::Max(destAxis.GetXmax(), anAxis.GetXmax());
Axis_t width = TMath::Max(width1, width2);
// check the bin size
if (!AlmostInteger(width/width1) || !AlmostInteger(width/width2))
return kFALSE;
// check the limits
Axis_t delta;
delta = (destAxis.GetXmin() - xmin)/width1;
if (!AlmostInteger(delta))
xmin -= (TMath::Ceil(delta) - delta)*width1;
delta = (anAxis.GetXmin() - xmin)/width2;
if (!AlmostInteger(delta))
xmin -= (TMath::Ceil(delta) - delta)*width2;
delta = (destAxis.GetXmin() - xmin)/width1;
if (!AlmostInteger(delta))
return kFALSE;
delta = (xmax - destAxis.GetXmax())/width1;
if (!AlmostInteger(delta))
xmax += (TMath::Ceil(delta) - delta)*width1;
delta = (xmax - anAxis.GetXmax())/width2;
if (!AlmostInteger(delta))
xmax += (TMath::Ceil(delta) - delta)*width2;
delta = (xmax - destAxis.GetXmax())/width1;
if (!AlmostInteger(delta))
return kFALSE;
#ifdef DEBUG
if (!AlmostInteger((xmax - xmin) / width)) { // unnecessary check
printf("TH1::RecomputeAxisLimits - Impossible\n");
return kFALSE;
}
#endif
destAxis.Set(TMath::Nint((xmax - xmin)/width), xmin, xmax);
return kTRUE;
}
//______________________________________________________________________________
Long64_t TH1::Merge(TCollection *li)
{
// Add all histograms in the collection to this histogram.
// This function computes the min/max for the x axis,
// compute a new number of bins, if necessary,
// add bin contents, errors and statistics.
// If all histograms have bin labels, bins with identical labels
// will be merged, no matter what their order is.
// If overflows are present and limits are different the function will fail.
// The function returns the total number of entries in the result histogram
// if the merge is successfull, -1 otherwise.
//
// IMPORTANT remark. The axis x may have different number
// of bins and different limits, BUT the largest bin width must be
// a multiple of the smallest bin width and the upper limit must also
// be a multiple of the bin width.
// Example:
// void atest() {
// TH1F *h1 = new TH1F("h1","h1",110,-110,0);
// TH1F *h2 = new TH1F("h2","h2",220,0,110);
// TH1F *h3 = new TH1F("h3","h3",330,-55,55);
// TRandom r;
// for (Int_t i=0;i<10000;i++) {
// h1->Fill(r.Gaus(-55,10));
// h2->Fill(r.Gaus(55,10));
// h3->Fill(r.Gaus(0,10));
// }
//
// TList *list = new TList;
// list->Add(h1);
// list->Add(h2);
// list->Add(h3);
// TH1F *h = (TH1F*)h1->Clone("h");
// h->Reset();
// h.Merge(list);
// h->Draw();
// }
if (!li) return 0;
if (li->IsEmpty()) return (Int_t) GetEntries();
TList inlist;
TH1* hclone = (TH1*)Clone("FirstClone");
BufferEmpty(1); // To remove buffer.
Reset(); // BufferEmpty sets limits so we can't use it later.
SetEntries(0);
inlist.Add(hclone);
inlist.AddAll(li);
THashList allLabels;
THashList* labels=GetXaxis()->GetLabels();
Bool_t haveOneLabel=kFALSE;
if (labels) {
TIter iL(labels);
TObjString* lb;
while ((lb=(TObjString*)iL())) {
haveOneLabel |= (lb && lb->String().Length());
if (!allLabels.FindObject(lb))
allLabels.Add(lb);
}
}
TAxis newXAxis;
Bool_t initialLimitsFound = kFALSE;
Bool_t allHaveLabels = haveOneLabel;
Bool_t same = kTRUE;
Bool_t allHaveLimits = kTRUE;
TIter next(&inlist);
while (TObject *o = next()) {
TH1* h = dynamic_cast<TH1*> (o);
if (!h) {
Error("Add","Attempt to add object of class: %s to a %s",
o->ClassName(),this->ClassName());
return -1;
}
Bool_t hasLimits = h->GetXaxis()->GetXmin() < h->GetXaxis()->GetXmax();
allHaveLimits = allHaveLimits && hasLimits;
if (hasLimits) {
h->BufferEmpty();
if (!initialLimitsFound) {
initialLimitsFound = kTRUE;
newXAxis.Set(h->GetXaxis()->GetNbins(), h->GetXaxis()->GetXmin(),
h->GetXaxis()->GetXmax());
}
else {
if (!RecomputeAxisLimits(newXAxis, *(h->GetXaxis()))) {
Error("Merge", "Cannot merge histograms - limits are inconsistent:\n "
"first: (%d, %f, %f), second: (%d, %f, %f)",
newXAxis.GetNbins(), newXAxis.GetXmin(), newXAxis.GetXmax(),
h->GetXaxis()->GetNbins(), h->GetXaxis()->GetXmin(),
h->GetXaxis()->GetXmax());
}
}
}
if (allHaveLabels) {
THashList* labels=h->GetXaxis()->GetLabels();
Bool_t haveOneLabel=kFALSE;
if (labels) {
TIter iL(labels);
TObjString* lb;
while ((lb=(TObjString*)iL())) {
haveOneLabel |= (lb && lb->String().Length());
if (!allLabels.FindObject(lb)) {
allLabels.Add(lb);
same = kFALSE;
}
}
}
allHaveLabels&=(labels && haveOneLabel);
if (!allHaveLabels)
Warning("Merge","Not all histograms have labels. I will ignore labels,"
" falling back to bin numbering mode.");
}
}
next.Reset();
same = same && SameLimitsAndNBins(newXAxis, *GetXaxis());
if (!same && initialLimitsFound)
SetBins(newXAxis.GetNbins(), newXAxis.GetXmin(), newXAxis.GetXmax());
if (!allHaveLimits) {
// fill this histogram with all the data from buffers of histograms without limits
while (TH1* h = (TH1*)next()) {
if (h->GetXaxis()->GetXmin() >= h->GetXaxis()->GetXmax() && h->fBuffer) {
// no limits
Int_t nbentries = (Int_t)h->fBuffer[0];
for (Int_t i = 0; i < nbentries; i++)
Fill(h->fBuffer[2*i + 2], h->fBuffer[2*i + 1]);
// Entries from buffers have to be filled one by one
// because FillN doesn't resize histograms.
}
}
if (!initialLimitsFound)
return (Int_t) GetEntries(); // all histograms have been processed
next.Reset();
}
//merge bin contents and errors
Stat_t stats[kNstat], totstats[kNstat];
for (Int_t i=0;i<kNstat;i++) {totstats[i] = stats[i] = 0;}
GetStats(totstats);
Stat_t nentries = GetEntries();
Int_t binx, ix, nx;
Double_t cu;
Bool_t canRebin=TestBit(kCanRebin);
ResetBit(kCanRebin); // reset, otherwise setting the under/overflow will rebin
while (TH1* h=(TH1*)next()) {
// process only if the histogram has limits; otherwise it was processed before
if (h->GetXaxis()->GetXmin() < h->GetXaxis()->GetXmax()) {
// import statistics
h->GetStats(stats);
for (Int_t i=0;i<kNstat;i++)
totstats[i] += stats[i];
nentries += h->GetEntries();
nx = h->GetXaxis()->GetNbins();
for (binx = 0; binx <= nx + 1; binx++) {
cu = h->GetBinContent(binx);
if (!allHaveLabels || !binx || binx==nx+1) {
if ((!same) && (binx == 0 || binx == nx + 1)) {
if (cu != 0) {
Error("Merge", "Cannot merge histograms - the histograms have"
" different limits and undeflows/overflows are present."
" The initial histogram is now broken!");
return -1;
}
}
ix = fXaxis.FindBin(h->GetXaxis()->GetBinCenter(binx));
} else {
const char* label=h->GetXaxis()->GetBinLabel(binx);
if (!label) label="";
ix = fXaxis.FindBin(label);
}
AddBinContent(ix,cu);
if (fSumw2.fN) {
Double_t error1 = h->GetBinError(binx);
fSumw2.fArray[ix] += error1*error1;
}
}
}
}
if (canRebin) SetBit(kCanRebin);
//copy merged stats
PutStats(totstats);
SetEntries(nentries);
if (hclone) delete hclone;
return (Long64_t)nentries;
}
//______________________________________________________________________________
void TH1::Multiply(TF1 *f1, Double_t c1)
{
// Performs the operation: this = this*c1*f1
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
//
// Only bins inside the function range are recomputed.
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Multiply
if (!f1) {
Error("Add","Attempt to multiply by a non-existing function");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// - Add statistics
Double_t nEntries = fEntries;
Stat_t s1[10];
Int_t i;
for (i=0;i<10;i++) {s1[i] = 0;}
PutStats(s1);
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu,w;
Double_t xx[3];
Double_t *params = 0;
f1->InitArgs(xx,params);
for (binz=0;binz<=nbinsz+1;binz++) {
xx[2] = fZaxis.GetBinCenter(binz);
for (biny=0;biny<=nbinsy+1;biny++) {
xx[1] = fYaxis.GetBinCenter(biny);
for (binx=0;binx<=nbinsx+1;binx++) {
xx[0] = fXaxis.GetBinCenter(binx);
if (!f1->IsInside(xx)) continue;
TF1::RejectPoint(kFALSE);
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
Double_t error1 = GetBinError(bin);
cu = c1*f1->EvalPar(xx);
if (TF1::RejectedPoint()) continue;
w = GetBinContent(bin)*cu;
SetBinContent(bin,w);
if (fSumw2.fN) {
fSumw2.fArray[bin] = cu*cu*error1*error1;
}
}
}
}
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Multiply(const TH1 *h1)
{
// -*-*-*-*-*-*-*-*-*Multiply this histogram by h1*-*-*-*-*-*-*-*-*-*-*-*-*
// =============================
//
// this = this*h1
//
// If errors of this are available (TH1::Sumw2), errors are recalculated.
// Note that if h1 has Sumw2 set, Sumw2 is automatically called for this
// if not already set.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Multiply
if (!h1) {
Error("Multiply","Attempt to multiply by a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()) {
Error("Multiply","Attempt to multiply histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Multiply","Attempt to multiply histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 has Sumw2 set
if (fSumw2.fN == 0 && h1->GetSumw2N() != 0) Sumw2();
// - Reset statistics
Double_t nEntries = fEntries;
fEntries = fTsumw = 0;
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t c0,c1,w;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = GetBin(binx,biny,binz);
c0 = GetBinContent(bin);
c1 = h1->GetBinContent(bin);
w = c0*c1;
SetBinContent(bin,w);
fEntries++;
if (fSumw2.fN) {
Double_t e0 = GetBinError(bin);
Double_t e1 = h1->GetBinError(bin);
fSumw2.fArray[bin] = (e0*e0*c1*c1 + e1*e1*c0*c0);
}
}
}
}
Stat_t s[kNstat];
GetStats(s);
PutStats(s);
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Multiply(const TH1 *h1, const TH1 *h2, Double_t c1, Double_t c2, Option_t *option)
{
// -*-*-*Replace contents of this histogram by multiplication of h1 by h2*-*
// ================================================================
//
// this = (c1*h1)*(c2*h2)
//
// If errors of this are available (TH1::Sumw2), errors are recalculated.
// Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this
// if not already set.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Multiply
TString opt = option;
opt.ToLower();
// Bool_t binomial = kFALSE;
// if (opt.Contains("b")) binomial = kTRUE;
if (!h1 || !h2) {
Error("Multiply","Attempt to multiply by a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()
|| nbinsx != h2->GetNbinsX() || nbinsy != h2->GetNbinsY() || nbinsz != h2->GetNbinsZ()) {
Error("Multiply","Attempt to multiply histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Multiply","Attempt to multiply histograms with different axis limits");
}
if (fXaxis.GetXmin() != h2->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h2->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h2->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h2->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h2->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h2->fZaxis.GetXmax()) {
Warning("Multiply","Attempt to multiply histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 or h2 have Sumw2 set
if (fSumw2.fN == 0 && (h1->GetSumw2N() != 0 || h2->GetSumw2N() != 0)) Sumw2();
// - Reset statistics
Double_t nEntries = fEntries;
fEntries = fTsumw = fTsumw2 = fTsumwx = fTsumwx2 = 0;
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t b1,b2,w,d1,d2;
d1 = c1*c1;
d2 = c2*c2;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
b1 = h1->GetBinContent(bin);
b2 = h2->GetBinContent(bin);
w = (c1*b1)*(c2*b2);
SetBinContent(bin,w);
fEntries++;
if (fSumw2.fN) {
Double_t e1 = h1->GetBinError(bin);
Double_t e2 = h2->GetBinError(bin);
fSumw2.fArray[bin] = d1*d2*(e1*e1*b2*b2 + e2*e2*b1*b1);
}
}
}
}
Stat_t s[kNstat];
GetStats(s);
PutStats(s);
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Paint(Option_t *option)
{
// -*-*-*-*-*-*-*Control routine to paint any kind of histograms*-*-*-*-*-*-*
// ===============================================
//
// This function is automatically called by TCanvas::Update.
// (see TH1::Draw for the list of options)
GetPainter();
if (fPainter) {
if (strlen(option) > 0) fPainter->Paint(option);
else fPainter->Paint(fOption.Data());
}
}
//______________________________________________________________________________
TH1 *TH1::Rebin(Int_t ngroup, const char*newname)
{
// -*-*-*Rebin this histogram grouping ngroup bins together*-*-*-*-*-*-*-*-*
// ==================================================
// if newname is not blank a new temporary histogram hnew is created.
// else the current histogram is modified (default)
// The parameter ngroup indicates how many bins of this have to me merged
// into one bin of hnew
// If the original histogram has errors stored (via Sumw2), the resulting
// histograms has new errors correctly calculated.
//
// examples: if h1 is an existing TH1F histogram with 100 bins
// h1->Rebin(); //merges two bins in one in h1: previous contents of h1 are lost
// h1->Rebin(5); //merges five bins in one in h1
// TH1F *hnew = h1->Rebin(5,"hnew"); // creates a new histogram hnew
// //merging 5 bins of h1 in one bin
//
// NOTE: If ngroup is not an exact divider of the number of bins,
// the top limit of the rebinned histogram is changed
// to the upper edge of the bin=newbins*ngroup and the corresponding
// bins are added to the overflow bin.
// Statistics will be recomputed from the new bin contents.
Int_t nbins = fXaxis.GetNbins();
Axis_t xmin = fXaxis.GetXmin();
Axis_t xmax = fXaxis.GetXmax();
if ((ngroup <= 0) || (ngroup > nbins)) {
Error("Rebin", "Illegal value of ngroup=%d",ngroup);
return 0;
}
if (fDimension > 1 || InheritsFrom("TProfile")) {
Error("Rebin", "Operation valid on 1-D histograms only");
return 0;
}
Int_t newbins = nbins/ngroup;
// Save old bin contents into a new array
Double_t entries = fEntries;
Double_t *oldBins = new Double_t[nbins];
Int_t bin, i;
for (bin=0;bin<nbins;bin++) oldBins[bin] = GetBinContent(bin+1);
Double_t *oldErrors = 0;
if (fSumw2.fN != 0) {
oldErrors = new Double_t[nbins];
for (bin=0;bin<nbins;bin++) oldErrors[bin] = GetBinError(bin+1);
}
// create a clone of the old histogram if newname is specified
TH1 *hnew = this;
if (newname && strlen(newname) > 0) {
hnew = (TH1*)Clone();
hnew->SetName(newname);
}
// change axis specs and rebuild bin contents array::RebinAx
if(newbins*ngroup != nbins) {
xmax = fXaxis.GetBinUpEdge(newbins*ngroup);
hnew->fTsumw = 0; //stats must be reset because top bins will be moved to overflow bin
}
// save the TAttAxis members (reset by SetBins)
Int_t nDivisions = fXaxis.GetNdivisions();
Color_t axisColor = fXaxis.GetAxisColor();
Color_t labelColor = fXaxis.GetLabelColor();
Style_t labelFont = fXaxis.GetLabelFont();
Float_t labelOffset = fXaxis.GetLabelOffset();
Float_t labelSize = fXaxis.GetLabelSize();
Float_t tickLength = fXaxis.GetTickLength();
Float_t titleOffset = fXaxis.GetTitleOffset();
Float_t titleSize = fXaxis.GetTitleSize();
Color_t titleColor = fXaxis.GetTitleColor();
Style_t titleFont = fXaxis.GetTitleFont();
if(fXaxis.GetXbins()->GetSize() > 0){ // variable bin sizes
Axis_t *bins = new Axis_t[newbins+1];
for(Int_t i = 0; i <= newbins; ++i) bins[i] = fXaxis.GetBinLowEdge(1+i*ngroup);
hnew->SetBins(newbins,bins); //this also changes errors array (if any)
delete [] bins;
} else {
hnew->SetBins(newbins,xmin,xmax); //this also changes errors array (if any)
}
// Restore axis attributes
fXaxis.SetNdivisions(nDivisions);
fXaxis.SetAxisColor(axisColor);
fXaxis.SetLabelColor(labelColor);
fXaxis.SetLabelFont(labelFont);
fXaxis.SetLabelOffset(labelOffset);
fXaxis.SetLabelSize(labelSize);
fXaxis.SetTickLength(tickLength);
fXaxis.SetTitleOffset(titleOffset);
fXaxis.SetTitleSize(titleSize);
fXaxis.SetTitleColor(titleColor);
fXaxis.SetTitleFont(titleFont);
// copy merged bin contents (ignore under/overflows)
Int_t oldbin = 0;
Double_t binContent, binError;
for (bin = 0;bin<=newbins;bin++) {
binContent = 0;
binError = 0;
for (i=0;i<ngroup;i++) {
if (oldbin+i >= nbins) break;
binContent += oldBins[oldbin+i];
if (oldErrors) binError += oldErrors[oldbin+i]*oldErrors[oldbin+i];
}
hnew->SetBinContent(bin+1,binContent);
if (oldErrors) hnew->SetBinError(bin+1,TMath::Sqrt(binError));
oldbin += ngroup;
}
hnew->SetEntries(entries); //was modified by SetBinContent
delete [] oldBins;
if (oldErrors) delete [] oldErrors;
return hnew;
}
//______________________________________________________________________________
Bool_t TH1::FindNewAxisLimits(const TAxis* axis, const Axis_t point, Axis_t& newMin, Axis_t &newMax)
{
// finds new limits for the axis so that *point* is within the range and
// the limits are compatible with the previous ones (see TH1::Merge).
// new limits are put into *newMin* and *newMax* variables.
// axis - axis whose limits are to be recomputed
// point - point that should fit within the new axis limits
// newMin - new minimum will be stored here
// newMax - new maximum will be stored here.
// false if failed (e.g. if the initial axis limits are wrong
// or the new range is more than 2^64 times the old one).
Axis_t xmin = axis->GetXmin();
Axis_t xmax = axis->GetXmax();
if (xmin >= xmax) return kFALSE;
Axis_t range = xmax-xmin;
Axis_t binsize = range / axis->GetNbins();
//recompute new axis limits by doubling the current range
Int_t ntimes = 0;
while (point < xmin) {
if (ntimes++ > 64)
return kFALSE;
xmin = xmin - range;
range *= 2;
binsize *= 2;
// make sure that the merging will be correct
if ( xmin / binsize - TMath::Floor(xmin / binsize) >= 0.5) {
xmin += 0.5 * binsize;
xmax += 0.5 * binsize; // won't work with a histogram with only one bin, but I don't care
}
}
while (point >= xmax) {
if (ntimes++ > 64)
return kFALSE;
xmax = xmax + range;
range *= 2;
binsize *= 2;
// make sure that the merging will be correct
if ( xmin / binsize - TMath::Floor(xmin / binsize) >= 0.5) {
xmin -= 0.5 * binsize;
xmax -= 0.5 * binsize; // won't work with a histogram with only one bin, but I don't care
}
}
newMin = xmin;
newMax = xmax;
// Info("FindNewAxisLimits", "OldAxis: (%lf, %lf), new: (%lf, %lf), point: %lf",
// axis->GetXmin(), axis->GetXmax(), xmin, xmax, point);
return kTRUE;
}
//______________________________________________________________________________
void TH1::RebinAxis(Axis_t x, const char *ax)
{
// Histogram is resized along ax such that x is in the axis range.
// The new axis limits are recomputed by doubling iteratively
// the current axis range until the specified value x is within the limits.
// The algorithm makes a copy of the histogram, then loops on all bins
// of the old histogram to fill the rebinned histogram.
// Takes into account errors (Sumw2) if any.
// The algorithm works for 1-d, 2-d and 3-d histograms.
// The bit kCanRebin must be set before invoking this function.
// Ex: h->SetBit(TH1::kCanRebin);
if (!TestBit(kCanRebin)) return;
if (TMath::IsNaN(x)) { // x may be a NaN
ResetBit(kCanRebin);
return;
}
char achoice = toupper(ax[0]);
TAxis *axis = &fXaxis;
if (achoice == 'Y') axis = &fYaxis;
if (achoice == 'Z') axis = &fZaxis;
if (axis->GetXmin() >= axis->GetXmax()) return;
if (axis->GetNbins() <= 0) return;
Axis_t xmin, xmax;
if (!FindNewAxisLimits(axis, x, xmin, xmax))
return;
//save a copy of this histogram
TH1 *hold = (TH1*)Clone();
hold->SetDirectory(0);
//set new axis limits
axis->SetLimits(xmin,xmax);
Int_t nbinsx = fXaxis.GetNbins();
Int_t nbinsy = fYaxis.GetNbins();
Int_t nbinsz = fZaxis.GetNbins();
//now loop on all bins and refill
Double_t err,cu;
Axis_t bx,by,bz;
Int_t errors = GetSumw2N();
Int_t ix,iy,iz,ibin,binx,biny,binz,bin;
Reset("ICE"); //reset only Integral, contents and Errors
for (binz=1;binz<=nbinsz;binz++) {
bz = hold->GetZaxis()->GetBinCenter(binz);
iz = fZaxis.FindFixBin(bz);
for (biny=1;biny<=nbinsy;biny++) {
by = hold->GetYaxis()->GetBinCenter(biny);
iy = fYaxis.FindFixBin(by);
for (binx=1;binx<=nbinsx;binx++) {
bx = hold->GetXaxis()->GetBinCenter(binx);
ix = fXaxis.FindFixBin(bx);
bin = hold->GetBin(binx,biny,binz);
ibin= GetBin(ix,iy,iz);
cu = hold->GetBinContent(bin);
AddBinContent(ibin,cu);
if (errors) {
err = hold->GetBinError(bin);
fSumw2.fArray[ibin] += err*err;
}
}
}
}
delete hold;
}
//______________________________________________________________________________
void TH1::RecursiveRemove(TObject *obj)
{
// Recursively remove object from the list of functions
if (fFunctions) {
if (!fFunctions->TestBit(kInvalidObject)) fFunctions->RecursiveRemove(obj);
}
}
//______________________________________________________________________________
void TH1::Scale(Double_t c1)
{
// -*-*-*Multiply this histogram by a constant c1*-*-*-*-*-*-*-*-*
// ========================================
//
// this = c1*this
//
// Note that both contents and errors(if any) are scaled.
// This function uses the services of TH1::Add
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Scale
Double_t ent = fEntries;
Add(this,this,c1,0);
fEntries = ent;
//if contours set, must also scale contours
Int_t ncontours = GetContour();
if (ncontours == 0) return;
Double_t *levels = fContour.GetArray();
for (Int_t i=0;i<ncontours;i++) {
levels[i] *= c1;
}
}
//______________________________________________________________________________
void TH1::SetDefaultBufferSize(Int_t buffersize)
{
// static function to set the default buffer size for automatic histograms.
// When an histogram is created with one of its axis lower limit greater
// or equal to its upper limit, the function SetBuffer is automatically
// called with the default buffer size.
if (buffersize < 0) buffersize = 0;
fgBufferSize = buffersize;
}
//______________________________________________________________________________
void TH1::SetTitle(const char *title)
{
// Change (i.e. set) the title
// if title is of the form "stringt;stringx;stringy;stringz"
// the histogram title is set to stringt,
// the x axis title to stringx, the y axis title to stringy,etc
fTitle = title;
// Decode fTitle. It may contain X, Y and Z titles
TString str1 = fTitle, str2;
Int_t isc = str1.Index(";");
Int_t lns = str1.Length();
if (isc >=0 ) {
fTitle = str1(0,isc);
str1 = str1(isc+1, lns);
isc = str1.Index(";");
if (isc >=0 ) {
str2 = str1(0,isc);
fXaxis.SetTitle(str2.Data());
lns = str1.Length();
str1 = str1(isc+1, lns);
isc = str1.Index(";");
if (isc >=0 ) {
str2 = str1(0,isc);
fYaxis.SetTitle(str2.Data());
lns = str1.Length();
str1 = str1(isc+1, lns);
fZaxis.SetTitle(str1.Data());
} else {
fYaxis.SetTitle(str1.Data());
}
} else {
fXaxis.SetTitle(str1.Data());
}
}
if (gPad && TestBit(kMustCleanup)) gPad->Modified();
}
// -------------------------------------------------------------------------
void TH1::SmoothArray(Int_t nn, Double_t *xx, Int_t ntimes)
{
// smooth array xx, translation of Hbook routine hsmoof.F
// based on algorithm 353QH twice presented by J. Friedman
// in Proc.of the 1974 CERN School of Computing, Norway, 11-24 August, 1974.
Int_t ii, jj, ik, jk, kk, nn1, nn2;
Double_t hh[6] = {0,0,0,0,0,0};
Double_t *yy = new Double_t[nn];
Double_t *zz = new Double_t[nn];
Double_t *rr = new Double_t[nn];
for (Int_t pass=0;pass<ntimes;pass++) {
// first copy original data into temp array
for (ii = 0; ii < nn; ii++) {
yy[ii] = xx[ii];
}
// do 353 i.e. running median 3, 5, and 3 in a single loop
for (kk = 1; kk <= 3; kk++) {
ik = 0;
if (kk == 2) ik = 1;
nn1 = ik + 2;
nn2 = nn - ik - 1;
// do all elements beside the first and last point for median 3
// and first two and last 2 for median 5
for (ii = nn1; ii <= nn2; ii++) {
for (jj = 0; jj < 3; jj++) {
hh[jj] = yy[ii + jj - 1];
}
zz[ii] = TMath::Median(3 + 2*ik, hh);
}
if (kk == 1) { // first median 3
// first point
hh[0] = 3*yy[1] - 2*yy[2];
hh[1] = yy[0];
hh[2] = yy[2];
zz[0] = TMath::Median(3, hh);
// last point
hh[0] = yy[nn - 2];
hh[1] = yy[nn - 1];
hh[2] = 3*yy[nn - 2] - 2*yy[nn - 3];
zz[nn - 1] = TMath::Median(3, hh);
}
if (kk == 2) { // median 5
// first point remains the same
zz[0] = yy[0];
for (ii = 0; ii < 3; ii++) {
hh[ii] = yy[ii];
}
zz[1] = TMath::Median(3, hh);
// last two points
for (ii = 0; ii < 3; ii++) {
hh[ii] = yy[nn +nn2 -1 + ii];
}
zz[nn - 2] = TMath::Median(3, hh);
zz[nn - 1] = yy[nn - 1];
}
}
// quadratic interpolation for flat segments
nn2 = nn2 - 2;
for (ii = nn1; ii <= nn2; ii++) {
if (zz[ii - 1] != zz[ii]) continue;
if (zz[ii] != zz[ii + 1]) continue;
hh[0] = zz[ii - 2] - zz[ii];
hh[1] = zz[ii + 2] - zz[ii];
if (hh[0] * hh[1] < 0) continue;
jk = 0;
if ( TMath::Abs(hh[1]) > TMath::Abs(hh[0]) ) jk = -1;
yy[ii] = -0.5*zz[ii - 2*jk] + zz[ii - jk]/0.75 + zz[ii + 2*jk] /6.;
yy[ii + jk] = 0.5*(zz[ii + 2*jk] - zz[ii - 2*jk]) + zz[ii - jk];
}
// running means
for (ii = 1; ii < nn - 1; ii++) {
rr[ii] = 0.25*yy[ii - 1] + 0.5*yy[ii] + 0.25*yy[ii + 1];
}
rr[0] = yy[0];
rr[nn - 1] = yy[nn - 1];
// now do the same for residuals
for (ii = 0; ii < nn; ii++) {
yy[ii] = xx[ii] - rr[ii];
}
// do 353 i.e. running median 3, 5, and 3 in a single loop
for (kk = 1; kk <= 3; kk++) {
ik = 0;
if (kk == 2) ik = 1;
nn1 = ik + 1;
nn2 = nn - ik - 1;
// do all elements beside the first and last point for median 3
// and first two and last 2 for median 5
for (ii = nn1; ii <= nn2; ii++) {
for (jj = 0; jj < 3; jj++) {
hh[jj] = yy[ii + jj - 1];
}
zz[ii] = TMath::Median(3 + 2*ik, hh);
}
if (kk == 1) { // first median 3
// first point
hh[0] = 3*yy[1] - 2*yy[2];
hh[1] = yy[0];
hh[2] = yy[2];
zz[0] = TMath::Median(3, hh);
// last point
hh[0] = yy[nn - 2];
hh[1] = yy[nn - 1];
hh[2] = 3*yy[nn - 2] - 2*yy[nn - 3];
zz[nn - 1] = TMath::Median(3, hh);
}
if (kk == 2) { // median 5
// first point remains the same
zz[0] = yy[0];
for (ii = 0; ii < 3; ii++) {
hh[ii] = yy[ii];
}
zz[1] = TMath::Median(3, hh);
// last two points
for (ii = 0; ii < 3; ii++) {
hh[ii] = yy[nn - 3 + ii];
}
zz[nn - 2] = TMath::Median(3, hh);
zz[nn - 1] = yy[nn - 1];
}
}
// quadratic interpolation for flat segments
nn2 = nn2 - 1;
for (ii = nn1 + 1; ii <= nn2; ii++) {
if (zz[ii - 1] != zz[ii]) continue;
if (zz[ii] != zz[ii + 1]) continue;
hh[0] = zz[ii - 2] - zz[ii];
hh[1] = zz[ii + 2] - zz[ii];
if (hh[0] * hh[1] < 0) continue;
jk = 0;
if ( TMath::Abs(hh[1]) > TMath::Abs(hh[0]) ) jk = -1;
yy[ii] = -0.5*zz[ii - 2*jk] + zz[ii - jk]/0.75 + zz[ii + 2*jk]/6.;
yy[ii + jk] = 0.5*(zz[ii + 2*jk] - zz[ii - 2*jk]) + zz[ii - jk];
}
// running means
for (ii = 1; ii <= nn - 1; ii++) {
zz[ii] = 0.25*yy[ii - 1] + 0.5*yy[ii] + 0.25*yy[ii + 1];
}
zz[0] = yy[0];
zz[nn - 1] = yy[nn - 1];
// add smoothed xx and smoothed residuals
for (ii = 0; ii < nn; ii++) {
if (xx[ii] < 0) xx[ii] = rr[ii] + zz[ii];
else xx[ii] = TMath::Abs(rr[ii] + zz[ii]);
}
}
delete [] yy;
delete [] zz;
delete [] rr;
}
// ------------------------------------------------------------------------
void TH1::Smooth(Int_t ntimes, Int_t firstbin, Int_t lastbin)
{
// Smooth bin contents of this histogram between firstbin and lastbin.
// (if firstbin=-1 and lastbin=-1 (default) all bins are smoothed.
// bin contents are replaced by their smooth values.
// Errors (if any) are not modified.
// algorithm can only be applied to 1-d histograms
if (fDimension != 1) {
Error("Smooth","Smooth only supported for 1-d histograms");
return;
}
Int_t nbins = fXaxis.GetNbins();
if (firstbin < 0) firstbin = 1;
if (lastbin < 0) lastbin = nbins;
if (lastbin > nbins+1) lastbin = nbins;
nbins = lastbin - firstbin + 1;
Double_t *xx = new Double_t[nbins];
Int_t i;
for (i=0;i<nbins;i++) {
xx[i] = GetBinContent(i+firstbin);
}
TH1::SmoothArray(nbins,xx,ntimes);
for (i=0;i<nbins;i++) {
SetBinContent(i+firstbin,xx[i]);
}
delete [] xx;
if (gPad) gPad->Modified();
}
// ------------------------------------------------------------------------
void TH1::StatOverflows(Bool_t flag)
{
// if flag=kTRUE, underflows and overflows are used by the Fill functions
// in the computation of statistics (mean value, RMS).
// By default, underflows or overflows are not used.
fgStatOverflows = flag;
}
//_______________________________________________________________________
void TH1::Streamer(TBuffer &b)
{
// -*-*-*-*-*-*-*Stream a class object*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
// =====================
if (b.IsReading()) {
UInt_t R__s, R__c;
Version_t R__v = b.ReadVersion(&R__s, &R__c);
if (R__v > 2) {
TH1::Class()->ReadBuffer(b, this, R__v, R__s, R__c);
fXaxis.SetParent(this);
fYaxis.SetParent(this);
fZaxis.SetParent(this);
if (fgAddDirectory && !gROOT->ReadingObject()) {
fDirectory = gDirectory;
if (!gDirectory->GetList()->FindObject(this)) gDirectory->Append(this);
}
ResetBit(kCanDelete);
return;
}
//process old versions before automatic schema evolution
TNamed::Streamer(b);
TAttLine::Streamer(b);
TAttFill::Streamer(b);
TAttMarker::Streamer(b);
b >> fNcells;
fXaxis.Streamer(b);
fYaxis.Streamer(b);
fZaxis.Streamer(b);
fXaxis.SetParent(this);
fYaxis.SetParent(this);
fZaxis.SetParent(this);
b >> fBarOffset;
b >> fBarWidth;
b >> fEntries;
b >> fTsumw;
b >> fTsumw2;
b >> fTsumwx;
b >> fTsumwx2;
if (R__v < 2) {
Float_t maximum, minimum, norm;
Float_t *contour=0;
b >> maximum; fMaximum = maximum;
b >> minimum; fMinimum = minimum;
b >> norm; fNormFactor = norm;
Int_t n = b.ReadArray(contour);
fContour.Set(n);
for (Int_t i=0;i<n;i++) fContour.fArray[i] = contour[i];
delete [] contour;
} else {
b >> fMaximum;
b >> fMinimum;
b >> fNormFactor;
fContour.Streamer(b);
}
fSumw2.Streamer(b);
fOption.Streamer(b);
fFunctions->Delete();
fFunctions->Streamer(b);
if (!gROOT->ReadingObject()) {
fDirectory = gDirectory;
if (!gDirectory->GetList()->FindObject(this)) gDirectory->Append(this);
}
b.CheckByteCount(R__s, R__c, TH1::IsA());
} else {
TH1::Class()->WriteBuffer(b,this);
}
}
//______________________________________________________________________________
void TH1::Print(Option_t *option) const
{
// -*-*-*-*-*Print some global quantities for this histogram*-*-*-*-*-*-*-*
// ===============================================
//
// If option "base" is given, number of bins and ranges are also printed
// If option "range" is given, bin contents and errors are also printed
// for all bins in the current range (default 1-->nbins)
// If option "all" is given, bin contents and errors are also printed
// for all bins including under and overflows.
//
printf( "TH1.Print Name = %s, Entries= %d, Total sum= %g\n",GetName(),Int_t(fEntries),GetSumOfWeights());
TString opt = option;
opt.ToLower();
Int_t all;
if (opt.Contains("all")) all = 0;
else if (opt.Contains("range")) all = 1;
else if (opt.Contains("base")) all = 2;
else return;
Int_t bin, binx, biny, binz;
Int_t firstx=0,lastx=0,firsty=0,lasty=0,firstz=0,lastz=0;
if (all == 0) {
lastx = fXaxis.GetNbins()+1;
if (fDimension > 1) lasty = fYaxis.GetNbins()+1;
if (fDimension > 2) lastz = fZaxis.GetNbins()+1;
} else {
firstx = fXaxis.GetFirst(); lastx = fXaxis.GetLast();
if (fDimension > 1) {firsty = fYaxis.GetFirst(); lasty = fYaxis.GetLast();}
if (fDimension > 2) {firstz = fZaxis.GetFirst(); lastz = fZaxis.GetLast();}
}
if (all== 2) {
printf(" Title = %s\n", GetTitle());
printf(" NbinsX= %d, xmin= %g, xmax=%g", fXaxis.GetNbins(), fXaxis.GetXmin(), fXaxis.GetXmax());
if( fDimension > 1) printf(", NbinsY= %d, ymin= %g, ymax=%g", fYaxis.GetNbins(), fYaxis.GetXmin(), fYaxis.GetXmax());
if( fDimension > 2) printf(", NbinsZ= %d, zmin= %g, zmax=%g", fZaxis.GetNbins(), fZaxis.GetXmin(), fZaxis.GetXmax());
printf("\n");
return;
}
Stat_t w,e;
Axis_t x,y,z;
if (fDimension == 1) {
for (binx=firstx;binx<=lastx;binx++) {
x = fXaxis.GetBinCenter(binx);
w = GetBinContent(binx);
e = GetBinError(binx);
if(fSumw2.fN) printf(" fSumw[%d]=%g, x=%g, error=%g\n",binx,w,x,e);
else printf(" fSumw[%d]=%g, x=%g\n",binx,w,x);
}
}
if (fDimension == 2) {
for (biny=firsty;biny<=lasty;biny++) {
y = fYaxis.GetBinCenter(biny);
for (binx=firstx;binx<=lastx;binx++) {
bin = GetBin(binx,biny);
x = fXaxis.GetBinCenter(binx);
w = GetBinContent(bin);
e = GetBinError(bin);
if(fSumw2.fN) printf(" fSumw[%d][%d]=%g, x=%g, y=%g, error=%g\n",binx,biny,w,x,y,e);
else printf(" fSumw[%d][%d]=%g, x=%g, y=%g\n",binx,biny,w,x,y);
}
}
}
if (fDimension == 3) {
for (binz=firstz;binz<=lastz;binz++) {
z = fZaxis.GetBinCenter(binz);
for (biny=firsty;biny<=lasty;biny++) {
y = fYaxis.GetBinCenter(biny);
for (binx=firstx;binx<=lastx;binx++) {
bin = GetBin(binx,biny,binz);
x = fXaxis.GetBinCenter(binx);
w = GetBinContent(bin);
e = GetBinError(bin);
if(fSumw2.fN) printf(" fSumw[%d][%d][%d]=%g, x=%g, y=%g, z=%g, error=%g\n",binx,biny,binz,w,x,y,z,e);
else printf(" fSumw[%d][%d][%d]=%g, x=%g, y=%g, z=%g\n",binx,biny,binz,w,x,y,z);
}
}
}
}
}
//______________________________________________________________________________
void TH1::Rebuild(Option_t *)
{
// Using the current bin info, recompute the arrays for contents and errors
SetBinsLength();
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::Reset(Option_t *option)
{
// -*-*-*-*-*-*Reset this histogram: contents, errors, etc*-*-*-*-*-*-*-*
// ===========================================
//
// if option "ICE" is specified, resets only Integral, Contents and Errors.
TString opt = option;
opt.ToUpper();
fSumw2.Reset();
if (fIntegral) {delete [] fIntegral; fIntegral = 0;}
if (opt.Contains("ICE")) return;
if (fBuffer) BufferEmpty();
fTsumw = 0;
fTsumw2 = 0;
fTsumwx = 0;
fTsumwx2 = 0;
fEntries = 0;
TObject *stats = fFunctions->FindObject("stats");
fFunctions->Remove(stats);
//special logic to support the case where the same object is
//added multiple times in fFunctions.
//This case happens when the same object is added with different
//drawing modes
TObject *obj;
while ((obj = fFunctions->First())) {
while(fFunctions->Remove(obj));
delete obj;
}
if(stats) fFunctions->Add(stats);
fContour.Set(0);
}
//______________________________________________________________________________
void TH1::SavePrimitive(ofstream &out, Option_t *option)
{
// Save primitive as a C++ statement(s) on output stream out
Bool_t nonEqiX = kFALSE;
Bool_t nonEqiY = kFALSE;
Bool_t nonEqiZ = kFALSE;
Int_t i;
// Check if the histogram has equidistant X bins or not. If not, we
// create an array holding the bins.
if (GetXaxis()->GetXbins()->fN && GetXaxis()->GetXbins()->fArray) {
nonEqiX = kTRUE;
out << " Double_t xAxis[" << GetXaxis()->GetXbins()->fN
<< "] = {";
for (i = 0; i < GetXaxis()->GetXbins()->fN; i++) {
if (i != 0) out << ", ";
out << GetXaxis()->GetXbins()->fArray[i];
}
out << "}; " << endl;
}
// If the histogram is 2 or 3 dimensional, check if the histogram
// has equidistant Y bins or not. If not, we create an array
// holding the bins.
if (fDimension > 1 && GetYaxis()->GetXbins()->fN &&
GetYaxis()->GetXbins()->fArray) {
nonEqiY = kTRUE;
out << " Double_t yAxis[" << GetYaxis()->GetXbins()->fN
<< "] = {";
for (i = 0; i < GetYaxis()->GetXbins()->fN; i++) {
if (i != 0) out << ", ";
out << GetYaxis()->GetXbins()->fArray[i];
}
out << "}; " << endl;
}
// IF the histogram is 3 dimensional, check if the histogram
// has equidistant Z bins or not. If not, we create an array
// holding the bins.
if (fDimension > 2 && GetZaxis()->GetXbins()->fN &&
GetZaxis()->GetXbins()->fArray) {
nonEqiZ = kTRUE;
out << " Double_t zAxis[" << GetZaxis()->GetXbins()->fN
<< "] = {";
for (i = 0; i < GetZaxis()->GetXbins()->fN; i++) {
if (i != 0) out << ", ";
out << GetZaxis()->GetXbins()->fArray[i];
}
out << "}; " << endl;
}
char quote = '"';
out <<" "<<endl;
out <<" "<<"TH1"<<" *";
out << GetName() << " = new " << ClassName() << "(" << quote
<< GetName() << quote << "," << quote<< GetTitle() << quote
<< "," << GetXaxis()->GetNbins();
if (nonEqiX)
out << ", xAxis";
else
out << "," << GetXaxis()->GetXmin()
<< "," << GetXaxis()->GetXmax();
if (fDimension > 1) {
out << "," << GetYaxis()->GetNbins();
if (nonEqiY)
out << ", yAxis";
else
out << "," << GetYaxis()->GetXmin()
<< "," << GetYaxis()->GetXmax();
}
if (fDimension > 2) {
out << "," << GetZaxis()->GetNbins();
if (nonEqiZ)
out << ", zAxis";
else
out << "," << GetZaxis()->GetXmin()
<< "," << GetZaxis()->GetXmax();
}
out << ");" << endl;
// save bin contents
Int_t bin;
for (bin=0;bin<fNcells;bin++) {
Double_t bc = GetBinContent(bin);
if (bc) {
out<<" "<<GetName()<<"->SetBinContent("<<bin<<","<<bc<<");"<<endl;
}
}
// save bin errors
if (fSumw2.fN) {
for (bin=0;bin<fNcells;bin++) {
Double_t be = GetBinError(bin);
if (be) {
out<<" "<<GetName()<<"->SetBinError("<<bin<<","<<be<<");"<<endl;
}
}
}
TH1::SavePrimitiveHelp(out, option);
}
//______________________________________________________________________________
void TH1::SavePrimitiveHelp(ofstream &out, Option_t *option)
{
// helper function for the SavePrimitive functions from TH1
// or classes derived from TH1, eg TProfile, TProfile2D.
char quote = '"';
if (TMath::Abs(GetBarOffset()) > 1e-5) {
out<<" "<<GetName()<<"->SetBarOffset("<<GetBarOffset()<<");"<<endl;
}
if (TMath::Abs(GetBarWidth()-1) > 1e-5) {
out<<" "<<GetName()<<"->SetBarWidth("<<GetBarWidth()<<");"<<endl;
}
if (fMinimum != -1111) {
out<<" "<<GetName()<<"->SetMinimum("<<fMinimum<<");"<<endl;
}
if (fMaximum != -1111) {
out<<" "<<GetName()<<"->SetMaximum("<<fMaximum<<");"<<endl;
}
if (fNormFactor != 0) {
out<<" "<<GetName()<<"->SetNormFactor("<<fNormFactor<<");"<<endl;
}
if (fEntries != 0) {
out<<" "<<GetName()<<"->SetEntries("<<fEntries<<");"<<endl;
}
if (fDirectory == 0) {
out<<" "<<GetName()<<"->SetDirectory(0);"<<endl;
}
if (TestBit(kNoStats)) {
out<<" "<<GetName()<<"->SetStats(0);"<<endl;
}
if (fOption.Length() != 0) {
out<<" "<<GetName()<<"->SetOption("<<quote<<fOption.Data()<<quote<<");"<<endl;
}
// save contour levels
Int_t ncontours = GetContour();
if (ncontours > 0) {
out<<" "<<GetName()<<"->SetContour("<<ncontours<<");"<<endl;
for (Int_t bin=0;bin<ncontours;bin++) {
out<<" "<<GetName()<<"->SetContourLevel("<<bin<<","<<GetContourLevel(bin)<<");"<<endl;
}
}
// save list of functions
TObjOptLink *lnk = (TObjOptLink*)fFunctions->FirstLink();
TObject *obj;
while (lnk) {
obj = lnk->GetObject();
obj->SavePrimitive(out,"nodraw");
if (obj->InheritsFrom("TF1")) {
out<<" "<<GetName()<<"->GetListOfFunctions()->Add("<<obj->GetName()<<");"<<endl;
} else if (obj->InheritsFrom("TPaveStats")) {
out<<" "<<GetName()<<"->GetListOfFunctions()->Add(ptstats);"<<endl;
out<<" ptstats->SetParent("<<GetName()<<"->GetListOfFunctions());"<<endl;
} else {
out<<" "<<GetName()<<"->GetListOfFunctions()->Add("<<obj->GetName()<<","<<quote<<lnk->GetOption()<<quote<<");"<<endl;
}
lnk = (TObjOptLink*)lnk->Next();
}
// save attributes
SaveFillAttributes(out,GetName(),0,1001);
SaveLineAttributes(out,GetName(),1,1,1);
SaveMarkerAttributes(out,GetName(),1,1,1);
fXaxis.SaveAttributes(out,GetName(),"->GetXaxis()");
fYaxis.SaveAttributes(out,GetName(),"->GetYaxis()");
fZaxis.SaveAttributes(out,GetName(),"->GetZaxis()");
TString opt = option;
opt.ToLower();
if (!opt.Contains("nodraw")) {
out<<" "<<GetName()<<"->Draw("
<<quote<<option<<quote<<");"<<endl;
}
}
//______________________________________________________________________________
void TH1::UseCurrentStyle()
{
// Copy current attributes from/to current style
if (gStyle->IsReading()) {
fXaxis.ResetAttAxis("X");
fYaxis.ResetAttAxis("Y");
fZaxis.ResetAttAxis("Z");
SetBarOffset(gStyle->GetBarOffset());
SetBarWidth(gStyle->GetBarWidth());
SetFillColor(gStyle->GetHistFillColor());
SetFillStyle(gStyle->GetHistFillStyle());
SetLineColor(gStyle->GetHistLineColor());
SetLineStyle(gStyle->GetHistLineStyle());
SetLineWidth(gStyle->GetHistLineWidth());
SetMarkerColor(gStyle->GetMarkerColor());
SetMarkerStyle(gStyle->GetMarkerStyle());
SetMarkerSize(gStyle->GetMarkerSize());
Int_t dostat = gStyle->GetOptStat();
if (gStyle->GetOptFit() && !dostat) dostat = 1000000001;
SetStats(dostat);
} else {
gStyle->SetBarOffset(fBarOffset);
gStyle->SetBarWidth(fBarWidth);
gStyle->SetHistFillColor(GetFillColor());
gStyle->SetHistFillStyle(GetFillStyle());
gStyle->SetHistLineColor(GetLineColor());
gStyle->SetHistLineStyle(GetLineStyle());
gStyle->SetHistLineWidth(GetLineWidth());
gStyle->SetMarkerColor(GetMarkerColor());
gStyle->SetMarkerStyle(GetMarkerStyle());
gStyle->SetMarkerSize(GetMarkerSize());
gStyle->SetOptStat(TestBit(kNoStats));
}
}
//______________________________________________________________________________
Double_t TH1::GetMean(Int_t axis) const
{
// For axis = 1,2 or 3 returns the mean value of the histogram along
// X,Y or Z axis.
// For axis = 11, 12, 13 returns the standard error of the mean value
// of the histogram along X, Y or Z axis
//
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
// -*-*-*-*-*-*Return mean value of this histogram along the X axis*-*-*-*-*
// ====================================================
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
if (axis<1 || axis>3&&axis<11 || axis>13) return 0;
Stat_t stats[kNstat];
for (Int_t i=4;i<kNstat;i++) stats[i] = 0;
GetStats(stats);
if (stats[0] == 0) return 0;
if (axis<10){
Int_t ax[3] = {2,4,7};
return stats[ax[axis-1]]/stats[0];
} else {
Double_t rms = GetRMS(axis-10);
return (rms/TMath::Sqrt(stats[0]));
}
}
//______________________________________________________________________________
Double_t TH1::GetMeanError(Int_t axis) const
{
// -*-*-*-*-*-*Return standard error of mean of this histogram along the X axis*-*-*-*-*
// ====================================================
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
// Also note, that although the definition of standard error doesn't include the
// assumption of normality, many uses of this feature implicitly assume it.
return GetMean(axis+10);
}
//______________________________________________________________________________
Double_t TH1::GetRMS(Int_t axis) const
{
// For axis = 1,2 or 3 returns the Sigma value of the histogram along
// X, Y or Z axis
// For axis = 11, 12 or 13 returns the error of RMS estimation along
// X, Y or Z axis for Normal distribution
//
// Note that the mean value/sigma is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
// Note that this function returns the Standard Deviation (Sigma)
// of the distribution (not RMS).
// The Sigma estimate is computed as Sqrt((1/N)*(Sum(x_i-x_mean)^2))
// The name "RMS" was introduced many years ago (Hbook/PAW times).
// We kept the name for continuity.
if (axis<1 || axis>3&&axis<11 || axis>13) return 0;
Stat_t x, rms2, stats[kNstat];
for (Int_t i=4;i<kNstat;i++) stats[i] = 0;
GetStats(stats);
if (stats[0] == 0) return 0;
Int_t ax[3] = {2,4,7};
Int_t axm = ax[axis%10 - 1];
x = stats[axm]/stats[0];
rms2 = TMath::Abs(stats[axm+1]/stats[0] -x*x);
if (axis<10)
return TMath::Sqrt(rms2);
else
return TMath::Sqrt(rms2/(2*stats[0]));
}
//______________________________________________________________________________
Double_t TH1::GetRMSError(Int_t axis) const
{
// Return error of RMS estimation for Normal distribution
//
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
// Value returned is standard deviation of sample standard deviation.
return GetRMS(axis+10);
}
//______________________________________________________________________________
Double_t TH1::GetSkewness(Int_t axis) const
{
//For axis = 1, 2 or 3 returns skewness of the histogram along x, y or z axis.
//For axis = 11, 12 or 13 returns the approximate standard error of skewness
//of the histogram along x, y or z axis
//Note, that since third and fourth moment are not calculated
//at the fill time, skewness and its standard error are computed bin by bin
const TAxis *ax;
if (axis==1 || axis==11) ax = &fXaxis;
else if (axis==2 || axis==12) ax = &fYaxis;
else if (axis==3 || axis==13) ax = &fZaxis;
else {
Error("GetSkewness", "illegal value of parameter");
return 0;
}
if (axis < 10) {
//compute skewness
Double_t x, w, mean, rms, rms3, sum=0;
mean = GetMean(axis);
rms = GetRMS(axis);
rms3 = rms*rms*rms;
Int_t bin;
Double_t np=0;
for (bin=ax->GetFirst(); bin<=ax->GetLast(); bin++){
x = GetBinCenter(bin);
w = GetBinContent(bin);
np+=w;
sum+=w*(x-mean)*(x-mean)*(x-mean);
}
sum/=np*rms3;
return sum;
} else {
//compute standard error of skewness
Int_t nbins = ax->GetNbins();
return TMath::Sqrt(6./nbins);
}
}
//______________________________________________________________________________
Double_t TH1::GetKurtosis(Int_t axis) const
{
//For axis =1, 2 or 3 returns kurtosis of the histogram along x, y or z axis.
//Kurtosis(gaussian(0, 1)) = 0.
//For axis =11, 12 or 13 returns the approximate standard error of kurtosis
//of the histogram along x, y or z axis
//Note, that since third and fourth moment are not calculated
//at the fill time, kurtosis and its standard error are computed bin by bin
const TAxis *ax;
if (axis==1 || axis==11) ax = &fXaxis;
else if (axis==2 || axis==12) ax = &fYaxis;
else if (axis==3 || axis==13) ax = &fZaxis;
else {
Error("GetKurtosis", "illegal value of parameter");
return 0;
}
if (axis < 10){
Double_t x, w, mean, rms, rms4, sum=0;
mean = GetMean(axis);
rms = GetRMS(axis);
rms4 = rms*rms*rms*rms;
Int_t bin;
Double_t np=0;
for (bin=ax->GetFirst(); bin<=ax->GetLast(); bin++){
x = GetBinCenter(bin);
w = GetBinContent(bin);
np+=w;
sum+=w*(x-mean)*(x-mean)*(x-mean)*(x-mean);
}
sum/=np*rms4;
return sum-3;
} else {
Int_t nbins = ax->GetNbins();
return TMath::Sqrt(24./nbins);
}
}
//______________________________________________________________________________
void TH1::GetStats(Stat_t *stats) const
{
// fill the array stats from the contents of this histogram
// The array stats must be correctly dimensionned in the calling program.
// stats[0] = sumw
// stats[1] = sumw2
// stats[2] = sumwx
// stats[3] = sumwx2
//
// If no axis-subrange is specified (via TAxis::SetRange), the array stats
// is simply a copy of the statistics quantities computed at filling time.
// If a sub-range is specified, the function recomputes these quantities
// from the bin contents in the current axis range.
//
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
if (fBuffer) ((TH1*)this)->BufferEmpty();
// Loop on bins (possibly including underflows/overflows)
Int_t bin, binx;
Stat_t w,err;
Axis_t x;
if (fTsumw == 0 || fXaxis.TestBit(TAxis::kAxisRange)) {
for (bin=0;bin<4;bin++) stats[bin] = 0;
for (binx=fXaxis.GetFirst();binx<=fXaxis.GetLast();binx++) {
x = fXaxis.GetBinCenter(binx);
w = TMath::Abs(GetBinContent(binx));
err = TMath::Abs(GetBinError(binx));
stats[0] += w;
stats[1] += err*err;
stats[2] += w*x;
stats[3] += w*x*x;
}
} else {
stats[0] = fTsumw;
stats[1] = fTsumw2;
stats[2] = fTsumwx;
stats[3] = fTsumwx2;
}
}
//______________________________________________________________________________
void TH1::PutStats(Stat_t *stats)
{
// Replace current statistics with the values in array stats
fTsumw = stats[0];
fTsumw2 = stats[1];
fTsumwx = stats[2];
fTsumwx2 = stats[3];
}
//______________________________________________________________________________
Stat_t TH1::GetSumOfWeights() const
{
// -*-*-*-*-*-*Return the sum of weights excluding under/overflows*-*-*-*-*
// ===================================================
Int_t bin,binx,biny,binz;
Stat_t sum =0;
for(binz=1; binz<=fZaxis.GetNbins(); binz++) {
for(biny=1; biny<=fYaxis.GetNbins(); biny++) {
for(binx=1; binx<=fXaxis.GetNbins(); binx++) {
bin = GetBin(binx,biny,binz);
sum += GetBinContent(bin);
}
}
}
return sum;
}
//______________________________________________________________________________
Stat_t TH1::Integral(Option_t *option) const
{
//Return integral of bin contents. Only bins in the bins range are considered.
// By default the integral is computed as the sum of bin contents in the range.
// if option "width" is specified, the integral is the sum of
// the bin contents multiplied by the bin width in x.
return Integral(fXaxis.GetFirst(),fXaxis.GetLast(),option);
}
//______________________________________________________________________________
Stat_t TH1::Integral(Int_t binx1, Int_t binx2, Option_t *option) const
{
//Return integral of bin contents between binx1 and binx2 for a 1-D histogram
// By default the integral is computed as the sum of bin contents in the range.
// if option "width" is specified, the integral is the sum of
// the bin contents multiplied by the bin width in x.
if (binx1 < 0) binx1 = 0;
Stat_t integral = 0;
// - Loop on bins in specified range
TString opt = option;
opt.ToLower();
Bool_t width = kFALSE;
if (opt.Contains("width")) width = kTRUE;
Int_t binx;
for (binx=binx1;binx<=binx2;binx++) {
if (width) integral += GetBinContent(binx)*fXaxis.GetBinWidth(binx);
else integral += GetBinContent(binx);
}
return integral;
}
//______________________________________________________________________________
Double_t TH1::KolmogorovTest(const TH1 *h2, Option_t *option) const
{
// Statistical test of compatibility in shape between
// THIS histogram and h2, using Kolmogorov test.
//
// Default: Ignore under- and overflow bins in comparison
//
// option is a character string to specify options
// "U" include Underflows in test (also for 2-dim)
// "O" include Overflows (also valid for 2-dim)
// "N" include comparison of normalizations
// "D" Put out a line of "Debug" printout
// "M" Return the Maximum Kolmogorov distance instead of prob
// "X" Run the pseudo experiments post-processor with the following procedure:
// make pseudoexperiments based on random values from the parent
// distribution and compare the KS distance of the pseudoexperiment
// to the parent distribution. Bin the KS distances in a histogram,
// and then take the integral of all the KS values above the value
// obtained from the original data to Monte Carlo distribution.
// The number of pseudo-experiments nEXPT is currently fixed at 1000.
// The function returns the integral.
// (thanks to Ben Kilminster to submit this procedure). Note that
// this option "X" is much slower.
//
// The returned function value is the probability of test
// (much less than one means NOT compatible)
//
// Code adapted by Rene Brun from original HBOOK routine HDIFF
//
// NOTE1
// A good description of the Kolmogorov test can be seen at:
// http://www.itl.nist.gov/div898/handbook/eda/section3/eda35g.htm
//
// NOTE2
// see also alternative function TH1::Chi2Test
// The Kolmogorov test is assumed to give better results than Chi2Test
// in case of histograms with low statistics.
//
// NOTE3 (Jan Conrad, Fred James)
// "The returned value PROB is calculated such that it will be
// uniformly distributed between zero and one for compatible histograms,
// provided the data are not binned (or the number of bins is very large
// compared with the number of events). Users who have access to unbinned
// data and wish exact confidence levels should therefore not put their data
// into histograms, but should call directly TMath::KolmogorovTest. On
// the other hand, since TH1 is a convenient way of collecting data and
// saving space, this function has been provided. However, the values of
// PROB for binned data will be shifted slightly higher than expected,
// depending on the effects of the binning. For example, when comparing two
// uniform distributions of 500 events in 100 bins, the values of PROB,
// instead of being exactly uniformly distributed between zero and one, have
// a mean value of about 0.56. We can apply a useful
// rule: As long as the bin width is small compared with any significant
// physical effect (for example the experimental resolution) then the binning
// cannot have an important effect. Therefore, we believe that for all
// practical purposes, the probability value PROB is calculated correctly
// provided the user is aware that:
// 1. The value of PROB should not be expected to have exactly the correct
// distribution for binned data.
// 2. The user is responsible for seeing to it that the bin widths are
// small compared with any physical phenomena of interest.
// 3. The effect of binning (if any) is always to make the value of PROB
// slightly too big. That is, setting an acceptance criterion of (PROB>0.05
// will assure that at most 5% of truly compatible histograms are rejected,
// and usually somewhat less."
TString opt = option;
opt.ToUpper();
Double_t prob = 0;
TH1 *h1 = (TH1*)this;
if (h2 == 0) return 0;
TAxis *axis1 = h1->GetXaxis();
TAxis *axis2 = h2->GetXaxis();
Int_t ncx1 = axis1->GetNbins();
Int_t ncx2 = axis2->GetNbins();
// Check consistency of dimensions
if (h1->GetDimension() != 1 || h2->GetDimension() != 1) {
Error("KolmogorovTest","Histograms must be 1-D\n");
return 0;
}
// Check consistency in number of channels
if (ncx1 != ncx2) {
Error("KolmogorovTest","Number of channels is different, %d and %d\n",ncx1,ncx2);
return 0;
}
// Check consistency in channel edges
Double_t difprec = 1e-5;
Double_t diff1 = TMath::Abs(axis1->GetXmin() - axis2->GetXmin());
Double_t diff2 = TMath::Abs(axis1->GetXmax() - axis2->GetXmax());
if (diff1 > difprec || diff2 > difprec) {
Error("KolmogorovTest","histograms with different binning");
return 0;
}
Bool_t afunc1 = kFALSE;
Bool_t afunc2 = kFALSE;
Double_t sum1 = 0, sum2 = 0;
Double_t ew1, ew2, w1 = 0, w2 = 0;
Int_t bin;
for (bin=1;bin<=ncx1;bin++) {
sum1 += h1->GetBinContent(bin);
sum2 += h2->GetBinContent(bin);
ew1 = h1->GetBinError(bin);
ew2 = h2->GetBinError(bin);
w1 += ew1*ew1;
w2 += ew2*ew2;
}
if (sum1 == 0) {
Error("KolmogorovTest","Histogram1 %s integral is zero\n",h1->GetName());
return 0;
}
if (sum2 == 0) {
Error("KolmogorovTest","Histogram2 %s integral is zero\n",h2->GetName());
return 0;
}
Double_t tsum1 = sum1;
Double_t tsum2 = sum2;
if (opt.Contains("U")) {
tsum1 += h1->GetBinContent(0);
tsum2 += h2->GetBinContent(0);
}
if (opt.Contains("O")) {
tsum1 += h1->GetBinContent(ncx1+1);
tsum2 += h2->GetBinContent(ncx1+1);
}
// Check if histograms are weighted.
// If number of entries = number of channels, probably histograms were
// not filled via Fill(), but via SetBinContent()
Double_t ne1 = h1->GetEntries();
Double_t ne2 = h2->GetEntries();
// look at first histogram
Double_t difsum1 = (ne1-tsum1)/tsum1;
Double_t esum1 = sum1;
if (difsum1 > difprec && Int_t(ne1) != ncx1) {
if (opt.Contains("U") || opt.Contains("O")) {
Warning("KolmogorovTest","U/O option with weighted events for hist:%s\n",h1->GetName());
}
if (h1->GetSumw2N() == 0) {
Warning("KolmogorovTest","Weighted events and no Sumw2, hist:%s\n",h1->GetName());
} else {
esum1 = sum1*sum1/w1; //number of equivalent entries
}
}
// look at second histogram
Double_t difsum2 = (ne2-tsum2)/tsum2;
Double_t esum2 = sum2;
if (difsum2 > difprec && Int_t(ne2) != ncx1) {
if (opt.Contains("U") || opt.Contains("O")) {
Warning("KolmogorovTest","U/O option with weighted events for hist:%s\n",h2->GetName());
}
if (h2->GetSumw2N() == 0) {
Warning("KolmogorovTest","Weighted events and no Sumw2, hist:%s\n",h2->GetName());
} else {
esum2 = sum2*sum2/w2; //number of equivalent entries
}
}
Double_t s1 = 1/tsum1;
Double_t s2 = 1/tsum2;
// Find largest difference for Kolmogorov Test
Double_t dfmax =0, rsum1 = 0, rsum2 = 0;
Int_t first = 1;
Int_t last = ncx1;
if (opt.Contains("U")) first = 0;
if (opt.Contains("O")) last = ncx1+1;
for (bin=first;bin<=last;bin++) {
rsum1 += s1*h1->GetBinContent(bin);
rsum2 += s2*h2->GetBinContent(bin);
dfmax = TMath::Max(dfmax,TMath::Abs(rsum1-rsum2));
}
// Get Kolmogorov probability
Double_t z, prb1=0, prb2=0, prb3=0;
if (afunc1) z = dfmax*TMath::Sqrt(esum2);
else if (afunc2) z = dfmax*TMath::Sqrt(esum1);
else z = dfmax*TMath::Sqrt(esum1*esum2/(esum1+esum2));
prob = TMath::KolmogorovProb(z);
if (opt.Contains("N")) {
// Combine probabilities for shape and normalization,
prb1 = prob;
Double_t resum1 = esum1; if (afunc1) resum1 = 0;
Double_t resum2 = esum2; if (afunc2) resum2 = 0;
Double_t d12 = esum1-esum2;
Double_t chi2 = d12*d12/(resum1+resum2);
prb2 = TMath::Prob(chi2,1);
// see Eadie et al., section 11.6.2
if (prob > 0 && prb2 > 0) prob *= prb2*(1-TMath::Log(prob*prb2));
else prob = 0;
}
// X option. Pseudo-experiments post-processor to determine KS probability
const Int_t nEXPT = 1000;
if (opt.Contains("X")) {
Double_t dSEXPT;
Bool_t addStatus = fgAddDirectory;
fgAddDirectory = kFALSE;
TH1F *hDistValues = new TH1F("hDistValues","KS distances",200,0,1);
TH1 *hExpt = (TH1*)Clone();
fgAddDirectory = addStatus;
// make nEXPT experiments (this should be a parameter)
for (Int_t i=0; i < nEXPT; i++) {
hExpt->Reset();
hExpt->FillRandom(h1,(Int_t)ne2);
dSEXPT = KolmogorovTest(hExpt,"M");
hDistValues->Fill(dSEXPT);
}
prb3 = hDistValues->Integral(hDistValues->FindBin(dfmax),200)/hDistValues->Integral();
delete hDistValues;
delete hExpt;
}
// debug printout
if (opt.Contains("D")) {
printf(" Kolmo Prob h1 = %s, sum1=%g\n",h1->GetName(),sum1);
printf(" Kolmo Prob h2 = %s, sum2=%g\n",h2->GetName(),sum2);
printf(" Kolmo Prob = %g, Max Dist = %g\n",prob,dfmax);
if (opt.Contains("N"))
printf(" Kolmo Prob = %f for shape alone, =%f for normalisation alone\n",prb1,prb2);
if (opt.Contains("X"))
printf(" Kolmo Prob = %f with %d pseudo-experiments\n",prb3,nEXPT);
}
// This numerical error condition should never occur:
if (TMath::Abs(rsum1-1) > 0.002) Warning("KolmogorovTest","Numerical problems with h1=%s\n",h1->GetName());
if (TMath::Abs(rsum2-1) > 0.002) Warning("KolmogorovTest","Numerical problems with h2=%s\n",h2->GetName());
if(opt.Contains("M")) return dfmax;
else if(opt.Contains("X")) return prb3;
else return prob;
}
//______________________________________________________________________________
void TH1::SetContent(const Stat_t *content)
{
// -*-*-*-*-*-*Replace bin contents by the contents of array content*-*-*-*
// =====================================================
Int_t bin;
Stat_t bincontent;
for (bin=0; bin<fNcells; bin++) {
bincontent = *(content + bin);
SetBinContent(bin, bincontent);
}
}
//______________________________________________________________________________
Int_t TH1::GetContour(Double_t *levels)
{
// Return contour values into array levels if pointer levels is non zero
//
// The function returns the number of contour levels.
// see GetContourLevel to return one contour only
//
Int_t nlevels = fContour.fN;
if (levels) {
if (nlevels == 0) {
nlevels = 20;
SetContour(nlevels);
} else {
if (TestBit(kUserContour) == 0) SetContour(nlevels);
}
for (Int_t level=0; level<nlevels; level++) levels[level] = fContour.fArray[level];
}
return nlevels;
}
//______________________________________________________________________________
Double_t TH1::GetContourLevel(Int_t level) const
{
// Return value of contour number level
// see GetContour to return the array of all contour levels
if (level <0 || level >= fContour.fN) return 0;
Double_t zlevel = fContour.fArray[level];
return zlevel;
}
//______________________________________________________________________________
Double_t TH1::GetContourLevelPad(Int_t level) const
{
// Return the value of contour number "level" in Pad coordinates ie: if the Pad
// is in log scale along Z it returns le log of the contour level value.
// see GetContour to return the array of all contour levels
if (level <0 || level >= fContour.fN) return 0;
Double_t zlevel = fContour.fArray[level];
// In case of user defined contours and Pad in log scale along Z,
// fContour.fArray doesn't contain the log of the contour whereas it does
// in case of equidistant contours.
if (gPad && gPad->GetLogz() && TestBit(kUserContour)) {
if (zlevel <= 0) return 0;
zlevel = TMath::Log10(zlevel);
}
return zlevel;
}
//______________________________________________________________________________
void TH1::SetBuffer(Int_t buffersize, Option_t * /*option*/)
{
// set the maximum number of entries to be kept in the buffer
if (fBuffer) {
BufferEmpty();
delete [] fBuffer;
fBuffer = 0;
}
if (buffersize <= 0) {
fBufferSize = 0;
return;
}
if (buffersize < 100) buffersize = 100;
fBufferSize = 1 + buffersize*(fDimension+1);
fBuffer = new Double_t[fBufferSize];
memset(fBuffer,0,8*fBufferSize);
}
//______________________________________________________________________________
void TH1::SetContour(Int_t nlevels, const Double_t *levels)
{
// -*-*-*-*-*-*Set the number and values of contour levels*-*-*-*-*-*-*-*-*
// ===========================================
//
// By default the number of contour levels is set to 20.
//
// if argument levels = 0 or missing, equidistant contours are computed
//
Int_t level;
ResetBit(kUserContour);
if (nlevels <=0 ) {
fContour.Set(0);
return;
}
fContour.Set(nlevels);
// - Contour levels are specified
if (levels) {
SetBit(kUserContour);
for (level=0; level<nlevels; level++) fContour.fArray[level] = levels[level];
} else {
// - contour levels are computed automatically as equidistant contours
Double_t zmin = GetMinimum();
Double_t zmax = GetMaximum();
if ((zmin == zmax) && (zmin != 0)) {
zmax += 0.01*TMath::Abs(zmax);
zmin -= 0.01*TMath::Abs(zmin);
}
Double_t dz = (zmax-zmin)/Double_t(nlevels);
if (gPad && gPad->GetLogz()) {
if (zmax <= 0) return;
if (zmin <= 0) zmin = 0.001*zmax;
zmin = TMath::Log10(zmin);
zmax = TMath::Log10(zmax);
dz = (zmax-zmin)/Double_t(nlevels);
}
for (level=0; level<nlevels; level++) {
fContour.fArray[level] = zmin + dz*Double_t(level);
}
}
}
//______________________________________________________________________________
void TH1::SetContourLevel(Int_t level, Double_t value)
{
// -*-*-*-*-*-*-*-*-*Set value for one contour level*-*-*-*-*-*-*-*-*-*-*-*
// ===============================
if (level <0 || level >= fContour.fN) return;
SetBit(kUserContour);
fContour.fArray[level] = value;
}
//______________________________________________________________________________
Double_t TH1::GetMaximum(Double_t maxval) const
{
// Return maximum value smaller than maxval of bins in the range*-*-*-*-*-*
if (fMaximum != -1111) return fMaximum;
Int_t bin, binx, biny, binz;
Int_t xfirst = fXaxis.GetFirst();
Int_t xlast = fXaxis.GetLast();
Int_t yfirst = fYaxis.GetFirst();
Int_t ylast = fYaxis.GetLast();
Int_t zfirst = fZaxis.GetFirst();
Int_t zlast = fZaxis.GetLast();
Double_t maximum = -FLT_MAX, value;
for (binz=zfirst;binz<=zlast;binz++) {
for (biny=yfirst;biny<=ylast;biny++) {
for (binx=xfirst;binx<=xlast;binx++) {
bin = GetBin(binx,biny,binz);
value = GetBinContent(bin);
if (value > maximum && value < maxval) maximum = value;
}
}
}
return maximum;
}
//______________________________________________________________________________
Int_t TH1::GetMaximumBin() const
{
// -*-*-*-*-*Return location of bin with maximum value in the range*-*
// ======================================================
Int_t locmax, locmay, locmaz;
return GetMaximumBin(locmax, locmay, locmaz);
}
//______________________________________________________________________________
Int_t TH1::GetMaximumBin(Int_t &locmax, Int_t &locmay, Int_t &locmaz) const
{
// -*-*-*-*-*Return location of bin with maximum value in the range*-*
// ======================================================
Int_t bin, binx, biny, binz;
Int_t locm;
Int_t xfirst = fXaxis.GetFirst();
Int_t xlast = fXaxis.GetLast();
Int_t yfirst = fYaxis.GetFirst();
Int_t ylast = fYaxis.GetLast();
Int_t zfirst = fZaxis.GetFirst();
Int_t zlast = fZaxis.GetLast();
Double_t maximum = -FLT_MAX, value;
locm = locmax = locmay = locmaz = 0;
for (binz=zfirst;binz<=zlast;binz++) {
for (biny=yfirst;biny<=ylast;biny++) {
for (binx=xfirst;binx<=xlast;binx++) {
bin = GetBin(binx,biny,binz);
value = GetBinContent(bin);
if (value > maximum) {
maximum = value;
locm = bin;
locmax = binx;
locmay = biny;
locmaz = binz;
}
}
}
}
return locm;
}
//______________________________________________________________________________
Double_t TH1::GetMinimum(Double_t minval) const
{
// Return minimum value greater than minval of bins in the range
if (fMinimum != -1111) return fMinimum;
Int_t bin, binx, biny, binz;
Int_t xfirst = fXaxis.GetFirst();
Int_t xlast = fXaxis.GetLast();
Int_t yfirst = fYaxis.GetFirst();
Int_t ylast = fYaxis.GetLast();
Int_t zfirst = fZaxis.GetFirst();
Int_t zlast = fZaxis.GetLast();
Double_t minimum=FLT_MAX, value;
for (binz=zfirst;binz<=zlast;binz++) {
for (biny=yfirst;biny<=ylast;biny++) {
for (binx=xfirst;binx<=xlast;binx++) {
bin = GetBin(binx,biny,binz);
value = GetBinContent(bin);
if (value < minimum && value > minval) minimum = value;
}
}
}
return minimum;
}
//______________________________________________________________________________
Int_t TH1::GetMinimumBin() const
{
// -*-*-*-*-*Return location of bin with minimum value in the range*-*
// ======================================================
Int_t locmix, locmiy, locmiz;
return GetMinimumBin(locmix, locmiy, locmiz);
}
//______________________________________________________________________________
Int_t TH1::GetMinimumBin(Int_t &locmix, Int_t &locmiy, Int_t &locmiz) const
{
// -*-*-*-*-*Return location of bin with minimum value in the range*-*
// ======================================================
Int_t bin, binx, biny, binz;
Int_t locm;
Int_t xfirst = fXaxis.GetFirst();
Int_t xlast = fXaxis.GetLast();
Int_t yfirst = fYaxis.GetFirst();
Int_t ylast = fYaxis.GetLast();
Int_t zfirst = fZaxis.GetFirst();
Int_t zlast = fZaxis.GetLast();
Double_t minimum = FLT_MAX, value;
locm = locmix = locmiy = locmiz = 0;
for (binz=zfirst;binz<=zlast;binz++) {
for (biny=yfirst;biny<=ylast;biny++) {
for (binx=xfirst;binx<=xlast;binx++) {
bin = GetBin(binx,biny,binz);
value = GetBinContent(bin);
if (value < minimum) {
minimum = value;
locm = bin;
locmix = binx;
locmiy = biny;
locmiz = binz;
}
}
}
}
return locm;
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, Axis_t xmin, Axis_t xmax)
{
// -*-*-*-*-*-*-*Redefine x axis parameters*-*-*-*-*-*-*-*-*-*-*-*
// ===========================
// The X axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
if (GetDimension() != 1) {
Error("SetBins","Operation only valid for 1-d histograms");
return;
}
fXaxis.SetRange(0,0);
fXaxis.Set(nx,xmin,xmax);
fYaxis.Set(1,0,1);
fZaxis.Set(1,0,1);
fNcells = nx+2;
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, const Axis_t *xBins)
{
// -*-*-*-*-*-*-*Redefine x axis parameters with variable bin sizes *-*-*-*-*-*-*-*-*-*
// ===================================================
// The X axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
// xBins is supposed to be of length nx+1
if (GetDimension() != 1) {
Error("SetBins","Operation only valid for 1-d histograms");
return;
}
fXaxis.SetRange(0,0);
fXaxis.Set(nx,xBins);
fYaxis.Set(1,0,1);
fZaxis.Set(1,0,1);
fNcells = nx+2;
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, Axis_t xmin, Axis_t xmax, Int_t ny, Axis_t ymin, Axis_t ymax)
{
// -*-*-*-*-*-*-*Redefine x and y axis parameters*-*-*-*-*-*-*-*-*-*-*-*
// =================================
// The X and Y axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
if (GetDimension() != 2) {
Error("SetBins","Operation only valid for 2-d histograms");
return;
}
fXaxis.SetRange(0,0);
fYaxis.SetRange(0,0);
fXaxis.Set(nx,xmin,xmax);
fYaxis.Set(ny,ymin,ymax);
fZaxis.Set(1,0,1);
fNcells = (nx+2)*(ny+2);
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, const Axis_t *xBins, Int_t ny, const Axis_t *yBins)
{
// -*-*-*-*-*-*-*Redefine x and y axis parameters with variable bin sizes *-*-*-*-*-*-*-*-*
// =========================================================
// The X and Y axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
// xBins is supposed to be of length nx+1, yBins is supposed to be of length ny+1
if (GetDimension() != 2) {
Error("SetBins","Operation only valid for 2-d histograms");
return;
}
fXaxis.SetRange(0,0);
fYaxis.SetRange(0,0);
fXaxis.Set(nx,xBins);
fYaxis.Set(ny,yBins);
fZaxis.Set(1,0,1);
fNcells = (nx+2)*(ny+2);
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, Axis_t xmin, Axis_t xmax, Int_t ny, Axis_t ymin, Axis_t ymax, Int_t nz, Axis_t zmin, Axis_t zmax)
{
// -*-*-*-*-*-*-*Redefine x, y and z axis parameters*-*-*-*-*-*-*-*-*-*-*-*
// ====================================
// The X, Y and Z axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
if (GetDimension() != 3) {
Error("SetBins","Operation only valid for 3-d histograms");
return;
}
fXaxis.SetRange(0,0);
fYaxis.SetRange(0,0);
fZaxis.SetRange(0,0);
fXaxis.Set(nx,xmin,xmax);
fYaxis.Set(ny,ymin,ymax);
fZaxis.Set(nz,zmin,zmax);
fNcells = (nx+2)*(ny+2)*(nz+2);
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetMaximum(Double_t maximum)
{
// -*-*-*-*-*-*-*Set the maximum value for the Y axis*-*-*-*-*-*-*-*-*-*-*-*
// ====================================
// By default the maximum value is automatically set to the maximum
// bin content plus a margin of 10 per cent.
// Use TH1::GetMaximum to find the maximum value of an histogram
// Use TH1::GetMaximumBin to find the bin with the maximum value of an histogram
//
fMaximum = maximum;
}
//______________________________________________________________________________
void TH1::SetMinimum(Double_t minimum)
{
// -*-*-*-*-*-*-*Set the minimum value for the Y axis*-*-*-*-*-*-*-*-*-*-*-*
// ====================================
// By default the minimum value is automatically set to zero if all bin contents
// are positive or the minimum - 10 per cent otherwise.
// Use TH1::GetMinimum to find the minimum value of an histogram
// Use TH1::GetMinimumBin to find the bin with the minimum value of an histogram
//
fMinimum = minimum;
}
//______________________________________________________________________________
void TH1::SetDirectory(TDirectory *dir)
{
// By default when an histogram is created, it is added to the list
// of histogram objects in the current directory in memory.
// Remove reference to this histogram from current directory and add
// reference to new directory dir. dir can be 0 in which case the
// histogram does not belong to any directory.
if (fDirectory == dir) return;
if (fDirectory) fDirectory->GetList()->Remove(this);
fDirectory = dir;
if (fDirectory) fDirectory->GetList()->Add(this);
}
//______________________________________________________________________________
void TH1::SetError(const Stat_t *error)
{
// -*-*-*-*-*-*-*Replace bin errors by values in array error*-*-*-*-*-*-*-*-*
// ===========================================
Int_t bin;
Stat_t binerror;
for (bin=0; bin<fNcells; bin++) {
binerror = error[bin];
SetBinError(bin, binerror);
}
}
//______________________________________________________________________________
void TH1::SetName(const char *name)
{
// Change the name of this histogram
//
// Histograms are named objects in a THashList.
// We must update the hashlist if we change the name
if (fDirectory) fDirectory->GetList()->Remove(this);
fName = name;
if (fDirectory) fDirectory->GetList()->Add(this);
}
//______________________________________________________________________________
void TH1::SetNameTitle(const char *name, const char *title)
{
// Change the name and title of this histogram
//
// Histograms are named objects in a THashList.
// We must update the hashlist if we change the name
if (fDirectory) fDirectory->GetList()->Remove(this);
fName = name;
SetTitle(title);
if (fDirectory) fDirectory->GetList()->Add(this);
}
//______________________________________________________________________________
void TH1::SetStats(Bool_t stats)
{
// -*-*-*-*-*-*-*Set statistics option on/off
// ============================
// By default, the statistics box is drawn.
// The paint options can be selected via gStyle->SetOptStats.
// This function sets/resets the kNoStats bin in the histogram object.
// It has priority over the Style option.
ResetBit(kNoStats);
if (!stats) {
SetBit(kNoStats);
//remove the "stats" object from the list of functions
if (fFunctions) delete fFunctions->FindObject("stats");
}
}
//______________________________________________________________________________
void TH1::Sumw2()
{
// -*-*-*Create structure to store sum of squares of weights*-*-*-*-*-*-*-*
// ===================================================
//
// if histogram is already filled, the sum of squares of weights
// is filled with the existing bin contents
//
// The error per bin will be computed as sqrt(sum of squares of weight)
// for each bin.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (fSumw2.fN) {
Warning("Sumw2","Sum of squares of weights structure already created");
return;
}
fSumw2.Set(fNcells);
for (Int_t bin=0; bin<fNcells; bin++) {
fSumw2.fArray[bin] = GetBinContent(bin);
}
}
//______________________________________________________________________________
TF1 *TH1::GetFunction(const char *name) const
{
// -*-*-*Return pointer to function with name*-*-*-*-*-*-*-*-*-*-*-*-*
// ===================================
//
// Functions such as TH1::Fit store the fitted function in the list of
// functions of this histogram.
return (TF1*)fFunctions->FindObject(name);
}
//______________________________________________________________________________
Stat_t TH1::GetBinError(Int_t bin) const
{
// -*-*-*-*-*Return value of error associated to bin number bin*-*-*-*-*
// ==================================================
//
// if the sum of squares of weights has been defined (via Sumw2),
// this function returns the sqrt(sum of w2).
// otherwise it returns the sqrt(contents) for this bin.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (fBuffer) ((TH1*)this)->BufferEmpty();
if (fSumw2.fN) return TMath::Sqrt(fSumw2.fArray[bin]);
Stat_t error2 = TMath::Abs(GetBinContent(bin));
return TMath::Sqrt(error2);
}
//______________________________________________________________________________
Stat_t TH1::GetBinError(Int_t binx, Int_t biny) const
{
// -*-*-*-*-*Return error of bin number binx, biny
// =====================================
// NB: Function to be called for 2-d histograms only
Int_t bin = GetBin(binx,biny);
return GetBinError(bin);
}
//______________________________________________________________________________
Stat_t TH1::GetBinError(Int_t binx, Int_t biny, Int_t binz) const
{
// -*-*-*-*-*Return error of bin number binx,biny,binz
// =========================================
// NB: Function to be called for 3-d histograms only
Int_t bin = GetBin(binx,biny,binz);
return GetBinError(bin);
}
//______________________________________________________________________________
Stat_t TH1::GetCellContent(Int_t binx, Int_t biny) const
{
// -*-*-*-*-*Return content of bin number binx, biny
// =====================================
// NB: Function to be called for 2-d histograms only
Int_t bin = GetBin(binx,biny);
return GetBinContent(bin);
}
//______________________________________________________________________________
Stat_t TH1::GetCellError(Int_t binx, Int_t biny) const
{
// -*-*-*-*-*Return error of bin number binx, biny
// =====================================
// NB: Function to be called for 2-d histograms only
Int_t bin = GetBin(binx,biny);
return GetBinError(bin);
}
//______________________________________________________________________________
void TH1::SetBinError(Int_t bin, Stat_t error)
{
// see convention for numbering bins in TH1::GetBin
if (!fSumw2.fN) Sumw2();
if (bin <0 || bin>= fSumw2.fN) return;
fSumw2.fArray[bin] = error*error;
}
//______________________________________________________________________________
void TH1::SetBinContent(Int_t binx, Int_t biny, Stat_t content)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
SetBinContent(biny*(fXaxis.GetNbins()+2) + binx,content);
}
//______________________________________________________________________________
void TH1::SetBinContent(Int_t binx, Int_t biny, Int_t binz, Stat_t content)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
if (binz <0 || binz>fZaxis.GetNbins()+1) return;
Int_t bin = GetBin(binx,biny,binz);
SetBinContent(bin,content);
}
//______________________________________________________________________________
void TH1::SetCellContent(Int_t binx, Int_t biny, Stat_t content)
{
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
SetBinContent(biny*(fXaxis.GetNbins()+2) + binx,content);
}
//______________________________________________________________________________
void TH1::SetBinError(Int_t binx, Int_t biny, Stat_t error)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
SetBinError(biny*(fXaxis.GetNbins()+2) + binx,error);
}
//______________________________________________________________________________
void TH1::SetBinError(Int_t binx, Int_t biny, Int_t binz, Stat_t error)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
if (binz <0 || binz>fZaxis.GetNbins()+1) return;
Int_t bin = GetBin(binx,biny,binz);
SetBinError(bin,error);
}
//______________________________________________________________________________
void TH1::SetCellError(Int_t binx, Int_t biny, Stat_t error)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
if (!fSumw2.fN) Sumw2();
Int_t bin = biny*(fXaxis.GetNbins()+2) + binx;
fSumw2.fArray[bin] = error*error;
}
//______________________________________________________________________________
void TH1::SetBinContent(Int_t, Stat_t)
{
// see convention for numbering bins in TH1::GetBin
AbstractMethod("SetBinContent");
}
ClassImp(TH1C)
//______________________________________________________________________________
// TH1C methods
//______________________________________________________________________________
TH1C::TH1C(): TH1(), TArrayC()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1C::TH1C(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type char (one byte per channel)
// ==========================================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayC::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1C::TH1C(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type char (one byte per channel)
// ==========================================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayC::Set(fNcells);
}
//______________________________________________________________________________
TH1C::TH1C(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type char (one byte per channel)
// ==========================================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayC::Set(fNcells);
}
//______________________________________________________________________________
TH1C::~TH1C()
{
}
//______________________________________________________________________________
TH1C::TH1C(const TH1C &h1c) : TH1(), TArrayC()
{
((TH1C&)h1c).Copy(*this);
}
//______________________________________________________________________________
void TH1C::AddBinContent(Int_t bin)
{
// -*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
if (fArray[bin] < 127) fArray[bin]++;
}
//______________________________________________________________________________
void TH1C::AddBinContent(Int_t bin, Stat_t w)
{
// -*-*-*-*-*-*-*-*Increment bin content by w*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
Int_t newval = fArray[bin] + Int_t(w);
if (newval > -128 && newval < 128) {fArray[bin] = Char_t(newval); return;}
if (newval < -127) fArray[bin] = -127;
if (newval > 127) fArray[bin] = 127;
}
//______________________________________________________________________________
void TH1C::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayC::Copy((TH1C&)newth1);
}
//______________________________________________________________________________
TH1 *TH1C::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1C *newth1 = (TH1C*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1C::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1C*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1C::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayC::Reset();
}
//______________________________________________________________________________
void TH1C::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = Char_t (content);
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = Char_t (content);
fEntries++;
}
//______________________________________________________________________________
void TH1C::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayC::Set(n);
}
//______________________________________________________________________________
TH1C& TH1C::operator=(const TH1C &h1)
{
if (this != &h1) ((TH1C&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1C operator*(Double_t c1, const TH1C &h1)
{
TH1C hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1C operator+(const TH1C &h1, const TH1C &h2)
{
TH1C hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1C operator-(const TH1C &h1, const TH1C &h2)
{
TH1C hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1C operator*(const TH1C &h1, const TH1C &h2)
{
TH1C hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1C operator/(const TH1C &h1, const TH1C &h2)
{
TH1C hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
ClassImp(TH1S)
//______________________________________________________________________________
// TH1S methods
//______________________________________________________________________________
TH1S::TH1S(): TH1(), TArrayS()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1S::TH1S(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type short
// ====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayS::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1S::TH1S(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type short
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayS::Set(fNcells);
}
//______________________________________________________________________________
TH1S::TH1S(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type short
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayS::Set(fNcells);
}
//______________________________________________________________________________
TH1S::~TH1S()
{
}
//______________________________________________________________________________
TH1S::TH1S(const TH1S &h1s) : TH1(), TArrayS()
{
((TH1S&)h1s).Copy(*this);
}
//______________________________________________________________________________
void TH1S::AddBinContent(Int_t bin)
{
// -*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
if (fArray[bin] < 32767) fArray[bin]++;
}
//______________________________________________________________________________
void TH1S::AddBinContent(Int_t bin, Stat_t w)
{
// Increment bin content by w
// ==========================
Int_t newval = fArray[bin] + Int_t(w);
if (newval > -32768 && newval < 32768) {fArray[bin] = Short_t(newval); return;}
if (newval < -32767) fArray[bin] = -32767;
if (newval > 32767) fArray[bin] = 32767;
}
//______________________________________________________________________________
void TH1S::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayS::Copy((TH1S&)newth1);
}
//______________________________________________________________________________
TH1 *TH1S::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1S *newth1 = (TH1S*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1S::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1S*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1S::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayS::Reset();
}
//______________________________________________________________________________
void TH1S::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = Short_t (content);
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = Short_t (content);
fEntries++;
}
//______________________________________________________________________________
void TH1S::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayS::Set(n);
}
//______________________________________________________________________________
TH1S& TH1S::operator=(const TH1S &h1)
{
if (this != &h1) ((TH1S&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1S operator*(Double_t c1, const TH1S &h1)
{
TH1S hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1S operator+(const TH1S &h1, const TH1S &h2)
{
TH1S hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1S operator-(const TH1S &h1, const TH1S &h2)
{
TH1S hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1S operator*(const TH1S &h1, const TH1S &h2)
{
TH1S hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1S operator/(const TH1S &h1, const TH1S &h2)
{
TH1S hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
ClassImp(TH1I)
//______________________________________________________________________________
// TH1I methods
//______________________________________________________________________________
TH1I::TH1I(): TH1(), TArrayI()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1I::TH1I(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type integer
// ====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayI::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1I::TH1I(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type integer
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayI::Set(fNcells);
}
//______________________________________________________________________________
TH1I::TH1I(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type integer
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayI::Set(fNcells);
}
//______________________________________________________________________________
TH1I::~TH1I()
{
}
//______________________________________________________________________________
TH1I::TH1I(const TH1I &h1i) : TH1(), TArrayI()
{
((TH1I&)h1i).Copy(*this);
}
//______________________________________________________________________________
void TH1I::AddBinContent(Int_t bin)
{
// -*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
if (fArray[bin] < 2147483647) fArray[bin]++;
}
//______________________________________________________________________________
void TH1I::AddBinContent(Int_t bin, Stat_t w)
{
// Increment bin content by w
// ==========================
Int_t newval = fArray[bin] + Int_t(w);
if (newval > -2147483647 && newval < 2147483647) {fArray[bin] = Int_t(newval); return;}
if (newval < -2147483647) fArray[bin] = -2147483647;
if (newval > 2147483647) fArray[bin] = 2147483647;
}
//______________________________________________________________________________
void TH1I::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayI::Copy((TH1I&)newth1);
}
//______________________________________________________________________________
TH1 *TH1I::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1I *newth1 = (TH1I*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1I::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1I*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1I::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayI::Reset();
}
//______________________________________________________________________________
void TH1I::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = Int_t (content);
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = Int_t (content);
fEntries++;
}
//______________________________________________________________________________
void TH1I::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayI::Set(n);
}
//______________________________________________________________________________
TH1I& TH1I::operator=(const TH1I &h1)
{
if (this != &h1) ((TH1I&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1I operator*(Double_t c1, const TH1I &h1)
{
TH1I hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1I operator+(const TH1I &h1, const TH1I &h2)
{
TH1I hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1I operator-(const TH1I &h1, const TH1I &h2)
{
TH1I hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1I operator*(const TH1I &h1, const TH1I &h2)
{
TH1I hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1I operator/(const TH1I &h1, const TH1I &h2)
{
TH1I hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
ClassImp(TH1F)
//______________________________________________________________________________
// TH1F methods
//______________________________________________________________________________
TH1F::TH1F(): TH1(), TArrayF()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1F::TH1F(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type float
// ====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayF::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1F::TH1F(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type float
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayF::Set(fNcells);
}
//______________________________________________________________________________
TH1F::TH1F(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type float
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayF::Set(fNcells);
}
//______________________________________________________________________________
TH1F::TH1F(const TVectorF &v)
: TH1("TVectorF","",v.GetNrows(),0,v.GetNrows())
{
// Create a histogram from a TVectorF
// by default the histogram name is "TVectorF" and title = ""
TArrayF::Set(fNcells);
fDimension = 1;
for (Int_t i=0;i<v.GetNrows();i++) {
SetBinContent(i+1,v(i));
}
TArrayF::Set(fNcells);
}
//______________________________________________________________________________
TH1F::TH1F(const TH1F &h) : TH1(), TArrayF()
{
((TH1F&)h).Copy(*this);
}
//______________________________________________________________________________
TH1F::~TH1F()
{
}
//______________________________________________________________________________
void TH1F::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayF::Copy((TH1F&)newth1);
}
//______________________________________________________________________________
TH1 *TH1F::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1F *newth1 = (TH1F*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1F::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1F*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1F::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayF::Reset();
}
//______________________________________________________________________________
void TH1F::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = Float_t (content);
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = Float_t (content);
fEntries++;
}
//______________________________________________________________________________
void TH1F::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayF::Set(n);
}
//______________________________________________________________________________
TH1F& TH1F::operator=(const TH1F &h1)
{
if (this != &h1) ((TH1F&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1F operator*(Double_t c1, const TH1F &h1)
{
TH1F hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1F operator+(const TH1F &h1, const TH1F &h2)
{
TH1F hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1F operator-(const TH1F &h1, const TH1F &h2)
{
TH1F hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1F operator*(const TH1F &h1, const TH1F &h2)
{
TH1F hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1F operator/(const TH1F &h1, const TH1F &h2)
{
TH1F hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
ClassImp(TH1D)
//______________________________________________________________________________
// TH1D methods
//______________________________________________________________________________
TH1D::TH1D(): TH1(), TArrayD()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1D::TH1D(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type double
// =====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayD::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1D::TH1D(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type double
// =====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayD::Set(fNcells);
}
//______________________________________________________________________________
TH1D::TH1D(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type double
// =====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayD::Set(fNcells);
}
//______________________________________________________________________________
TH1D::TH1D(const TVectorD &v)
: TH1("TVectorD","",v.GetNrows(),0,v.GetNrows())
{
// Create a histogram from a TVectorD
// by default the histogram name is "TVectorD" and title = ""
TArrayD::Set(fNcells);
fDimension = 1;
for (Int_t i=0;i<v.GetNrows();i++) {
SetBinContent(i+1,v(i));
}
TArrayD::Set(fNcells);
}
//______________________________________________________________________________
TH1D::~TH1D()
{
}
//______________________________________________________________________________
TH1D::TH1D(const TH1D &h1d) : TH1(), TArrayD()
{
((TH1D&)h1d).Copy(*this);
}
//______________________________________________________________________________
void TH1D::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayD::Copy((TH1D&)newth1);
}
//______________________________________________________________________________
TH1 *TH1D::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1D *newth1 = (TH1D*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1D::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1D*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1D::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayD::Reset();
}
//______________________________________________________________________________
void TH1D::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = content;
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = content;
fEntries++;
}
//______________________________________________________________________________
void TH1D::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayD::Set(n);
}
//______________________________________________________________________________
TH1D& TH1D::operator=(const TH1D &h1)
{
if (this != &h1) ((TH1D&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1D operator*(Double_t c1, const TH1D &h1)
{
TH1D hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1D operator+(const TH1D &h1, const TH1D &h2)
{
TH1D hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1D operator-(const TH1D &h1, const TH1D &h2)
{
TH1D hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1D operator*(const TH1D &h1, const TH1D &h2)
{
TH1D hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1D operator/(const TH1D &h1, const TH1D &h2)
{
TH1D hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1 *R__H(Int_t hid)
{
//return pointer to histogram with name
// hid if id >=0
// h_id if id <0
char hname[20];
if(hid >= 0) sprintf(hname,"h%d",hid);
else sprintf(hname,"h_%d",hid);
return (TH1*)gDirectory->Get(hname);
}
//______________________________________________________________________________
TH1 *R__H(const char * hname)
{
//return pointer to histogram with name hname
return (TH1*)gDirectory->Get(hname);
}
*/
//
TF1 *gF1=0; //left for back compatibility (use TVirtualFitter::GetUserFunc instead)
const Int_t kNstat = 11;
Int_t TH1::fgBufferSize = 1000;
Bool_t TH1::fgAddDirectory = kTRUE;
Bool_t TH1::fgStatOverflows= kFALSE;
extern void H1InitGaus();
extern void H1InitExpo();
extern void H1InitPolynom();
extern void H1LeastSquareFit(Int_t n, Int_t m, Double_t *a);
extern void H1LeastSquareLinearFit(Int_t ndata, Double_t &a0, Double_t &a1, Int_t &ifail);
extern void H1LeastSquareSeqnd(Int_t n, Double_t *a, Int_t idim, Int_t &ifail, Int_t k, Double_t *b);
ClassImp(TH1)
//______________________________________________________________________________
TH1::TH1(): TNamed(), TAttLine(), TAttFill(), TAttMarker()
{
// -*-*-*-*-*-*-*-*-*Histogram default constructor*-*-*-*-*-*-*-*-*-*-*-*-*
// =============================
fDirectory = 0;
fFunctions = new TList;
fNcells = 0;
fIntegral = 0;
fPainter = 0;
fEntries = 0;
fNormFactor = 0;
fTsumw = fTsumw2=fTsumwx=fTsumwx2=0;
fMaximum = -1111;
fMinimum = -1111;
fBufferSize = 0;
fBuffer = 0;
fXaxis.SetName("xaxis");
fYaxis.SetName("yaxis");
fZaxis.SetName("zaxis");
fXaxis.SetParent(this);
fYaxis.SetParent(this);
fZaxis.SetParent(this);
UseCurrentStyle();
}
//______________________________________________________________________________
TH1::~TH1()
{
// -*-*-*-*-*-*-*-*-*Histogram default destructor*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ============================
//TH1 *junk = 0;
//junk->SetLineColor(0);
if (!TestBit(kNotDeleted)) return;
if (fIntegral) {delete [] fIntegral; fIntegral = 0;}
if (fBuffer) {delete [] fBuffer; fBuffer = 0;}
if (fFunctions) {
fFunctions->SetBit(kInvalidObject);
TObject *obj;
//special logic to support the case where the same object is
//added multiple times in fFunctions.
//This case happens when the same object is added with different
//drawing modes
//In the loop below we must be careful with objects (eg TCutG) that may
// have been added to the list of functions of several histograms
//and may have been already deleted.
while ((obj = fFunctions->First())) {
while(fFunctions->Remove(obj));
if (!obj->TestBit(kNotDeleted)) break;
delete obj;
}
delete fFunctions;
}
if (fDirectory) {
if (!fDirectory->TestBit(TDirectory::kCloseDirectory))
fDirectory->GetList()->Remove(this);
}
fFunctions = 0;
fDirectory = 0;
delete fPainter;
}
//______________________________________________________________________________
TH1::TH1(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
:TNamed(name,title), TAttLine(), TAttFill(), TAttMarker()
{
// -*-*-*-*-*-*-*Normal constructor for fix bin size histograms*-*-*-*-*-*-*
// ==============================================
//
// Creates the main histogram structure:
// name : name of histogram (avoid blanks)
// title : histogram title
// if title is of the form "stringt;stringx;stringy;stringz"
// the histogram title is set to stringt,
// the x axis title to stringy, the y axis title to stringy,etc
// nbins : number of bins
// xlow : low edge of first bin
// xup : upper edge of last bin (not included in last bin)
//
// When an histogram is created, it is automatically added to the list
// of special objects in the current directory.
// To find the pointer to this histogram in the current directory
// by its name, do:
// TH1F *h1 = (TH1F*)gDirectory->FindObject(name);
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Build();
if (nbins <= 0) nbins = 1;
fXaxis.Set(nbins,xlow,xup);
fNcells = fXaxis.GetNbins()+2;
}
//______________________________________________________________________________
TH1::TH1(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
:TNamed(name,title), TAttLine(), TAttFill(), TAttMarker()
{
// -*-*-*-*-*Normal constructor for variable bin size histograms*-*-*-*-*-*-*
// ===================================================
//
// Creates the main histogram structure:
// name : name of histogram (avoid blanks)
// title : histogram title
// if title is of the form "stringt;stringx;stringy;stringz"
// the histogram title is set to stringt,
// the x axis title to stringy, the y axis title to stringy,etc
// nbins : number of bins
// xbins : array of low-edges for each bin
// This is an array of size nbins+1
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Build();
if (nbins <= 0) nbins = 1;
if (xbins) fXaxis.Set(nbins,xbins);
else fXaxis.Set(nbins,0,1);
fNcells = fXaxis.GetNbins()+2;
}
//______________________________________________________________________________
TH1::TH1(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
:TNamed(name,title), TAttLine(), TAttFill(), TAttMarker()
{
// -*-*-*-*-*Normal constructor for variable bin size histograms*-*-*-*-*-*-*
// ===================================================
//
// Creates the main histogram structure:
// name : name of histogram (avoid blanks)
// title : histogram title
// if title is of the form "stringt;stringx;stringy;stringz"
// the histogram title is set to stringt,
// the x axis title to stringy, the y axis title to stringy,etc
// nbins : number of bins
// xbins : array of low-edges for each bin
// This is an array of size nbins+1
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Build();
if (nbins <= 0) nbins = 1;
if (xbins) fXaxis.Set(nbins,xbins);
else fXaxis.Set(nbins,0,1);
fNcells = fXaxis.GetNbins()+2;
}
//______________________________________________________________________________
TH1::TH1(const TH1 &h) : TNamed(), TAttLine(), TAttFill(), TAttMarker()
{
// Copy constructor.
// The list of functions is not copied. (Use Clone if needed)
Copy((TObject&)h);
}
//______________________________________________________________________________
Bool_t TH1::AddDirectoryStatus()
{
//static function: cannot be inlined on Windows/NT
return fgAddDirectory;
}
//______________________________________________________________________________
void TH1::Browse(TBrowser *b)
{
Draw(b ? b->GetDrawOption() : "");
gPad->Update();
}
//______________________________________________________________________________
void TH1::Build()
{
// -*-*-*-*-*-*-*-*Creates histogram basic data structure*-*-*-*-*-*-*-*-*-*
// ======================================
fDirectory = 0;
fPainter = 0;
fIntegral = 0;
fEntries = 0;
fNormFactor = 0;
fTsumw = fTsumw2=fTsumwx=fTsumwx2=0;
fMaximum = -1111;
fMinimum = -1111;
fBufferSize = 0;
fBuffer = 0;
fXaxis.SetName("xaxis");
fYaxis.SetName("yaxis");
fZaxis.SetName("zaxis");
fYaxis.Set(1,0.,1.);
fZaxis.Set(1,0.,1.);
fXaxis.SetParent(this);
fYaxis.SetParent(this);
fZaxis.SetParent(this);
SetTitle(fTitle.Data());
fFunctions = new TList;
UseCurrentStyle();
if (fgAddDirectory && gDirectory) {
if (!gDirectory->GetList()) {
Warning("Build","Current directory is not a valid directory");
return;
}
TH1 *hold = (TH1*)gDirectory->GetList()->FindObject(GetName());
if (hold) {
Warning("Build","Replacing existing histogram: %s (Potential memory leak).",GetName());
gDirectory->GetList()->Remove(hold);
hold->SetDirectory(0);
// delete hold;
}
gDirectory->Append(this);
fDirectory = gDirectory;
}
}
//______________________________________________________________________________
void TH1::Add(TF1 *f1, Double_t c1, Option_t *option)
{
// Performs the operation: this = this + c1*f1
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
//
// By default, the function is computed at the centre of the bin.
// if option "I" is specified (1-d histogram only), the integral of the
// function in each bin is used instead of the value of the function at
// the centre of the bin.
// Only bins inside the function range are recomputed.
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Add
if (!f1) {
Error("Add","Attempt to add a non-existing function");
return;
}
TString opt = option;
opt.ToLower();
Bool_t integral = kFALSE;
if (opt.Contains("i") && fDimension ==1) integral = kTRUE;
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// - Add statistics
Stat_t s1[10];
Int_t i;
for (i=0;i<10;i++) {s1[i] = 0;}
PutStats(s1);
SetMinimum();
SetMaximum();
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu=0;
Double_t xx[3];
Double_t *params = 0;
f1->InitArgs(xx,params);
for (binz=0;binz<=nbinsz+1;binz++) {
xx[2] = fZaxis.GetBinCenter(binz);
for (biny=0;biny<=nbinsy+1;biny++) {
xx[1] = fYaxis.GetBinCenter(biny);
for (binx=0;binx<=nbinsx+1;binx++) {
xx[0] = fXaxis.GetBinCenter(binx);
if (!f1->IsInside(xx)) continue;
TF1::RejectPoint(kFALSE);
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
if (integral) {
xx[0] = fXaxis.GetBinLowEdge(binx);
cu = c1*f1->EvalPar(xx);
cu += c1*f1->Integral(fXaxis.GetBinLowEdge(binx),fXaxis.GetBinUpEdge(binx))*fXaxis.GetBinWidth(binx);
} else {
cu = c1*f1->EvalPar(xx);
}
if (TF1::RejectedPoint()) continue;
Double_t error1 = GetBinError(bin);
AddBinContent(bin,cu);
if (fSumw2.fN) {
//errors are unchanged: error on f1 assumed 0
fSumw2.fArray[bin] = error1*error1;
}
}
}
}
}
//______________________________________________________________________________
void TH1::Add(const TH1 *h1, Double_t c1)
{
// Performs the operation: this = this + c1*h1
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
// Note that if h1 has Sumw2 set, Sumw2 is automatically called for this
// if not already set.
//
// IMPORTANT NOTE1: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Add
//
// IMPORTANT NOTE2: if h1 has a normalisation factor, the normalisation factor
// is used , ie this = this + c1*factor*h1
// Use the other TH1::Add function if you do not want this feature
if (!h1) {
Error("Add","Attempt to add a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()) {
Error("Add","Attempt to add histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Add","Attempt to add histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 has Sumw2 set
if (fSumw2.fN == 0 && h1->GetSumw2N() != 0) Sumw2();
// - Add statistics
fEntries += c1*h1->GetEntries();
Stat_t s1[kNstat], s2[kNstat];
Int_t i;
for (i=0;i<kNstat;i++) {s1[i] = s2[i] = 0;}
GetStats(s1);
h1->GetStats(s2);
for (i=0;i<kNstat;i++) {
if (i == 1) s1[i] += c1*c1*s2[i];
else s1[i] += c1*s2[i];
}
PutStats(s1);
SetMinimum();
SetMaximum();
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu;
Double_t factor =1;
if (h1->GetNormFactor() != 0) factor = h1->GetNormFactor()/h1->GetSumOfWeights();;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
cu = c1*factor*h1->GetBinContent(bin);
AddBinContent(bin,cu);
if (fSumw2.fN) {
Double_t error1 = factor*h1->GetBinError(bin);
fSumw2.fArray[bin] += c1*c1*error1*error1;
}
}
}
}
}
//______________________________________________________________________________
void TH1::Add(const TH1 *h1, const TH1 *h2, Double_t c1, Double_t c2)
{
// -*-*-*Replace contents of this histogram by the addition of h1 and h2*-*-*
// ===============================================================
//
// this = c1*h1 + c2*h2
// if errors are defined (see TH1::Sumw2), errors are also recalculated
// Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this
// if not already set.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Add
if (!h1 || !h2) {
Error("Add","Attempt to add a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()
|| nbinsx != h2->GetNbinsX() || nbinsy != h2->GetNbinsY() || nbinsz != h2->GetNbinsZ()) {
Error("Add","Attempt to add histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Add","Attempt to add histograms with different axis limits");
}
if (fXaxis.GetXmin() != h2->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h2->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h2->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h2->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h2->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h2->fZaxis.GetXmax()) {
Warning("Add","Attempt to add histograms::Add with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 or h2 have Sumw2 set
if (fSumw2.fN == 0 && (h1->GetSumw2N() != 0 || h2->GetSumw2N() != 0)) Sumw2();
// - Add statistics
Double_t nEntries = c1*h1->GetEntries() + c2*h2->GetEntries();
Stat_t s1[kNstat], s2[kNstat], s3[kNstat];
Int_t i;
for (i=0;i<kNstat;i++) {s1[i] = s2[i] = s3[i] = 0;}
h1->GetStats(s1);
h2->GetStats(s2);
for (i=0;i<kNstat;i++) {
if (i == 1) s3[i] = c1*c1*s1[i] + c2*c2*s2[i];
else s3[i] = c1*s1[i] + c2*s2[i];
}
PutStats(s3);
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
cu = c1*h1->GetBinContent(bin)+ c2*h2->GetBinContent(bin);
SetBinContent(bin,cu);
if (fSumw2.fN) {
Double_t error1 = h1->GetBinError(bin);
Double_t error2 = h2->GetBinError(bin);
fSumw2.fArray[bin] = c1*c1*error1*error1 + c2*c2*error2*error2;
}
}
}
}
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::AddBinContent(Int_t)
{
// -*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
AbstractMethod("AddBinContent");
}
//______________________________________________________________________________
void TH1::AddBinContent(Int_t, Stat_t)
{
// -*-*-*-*-*-*-*-*Increment bin content by a weight w*-*-*-*-*-*-*-*-*-*-*
// ===================================
AbstractMethod("AddBinContent");
}
//______________________________________________________________________________
void TH1::AddDirectory(Bool_t add)
{
// Sets the flag controlling the automatic add of histograms in memory
//
// By default (fAddDirectory = kTRUE), histograms are automatically added
// to the list of objects in memory.
// Note that one histogram can be removed from its support directory
// by calling h->SetDirectory(0) or h->SetDirectory(dir) to add it
// to the list of objects in the directory dir.
//
// NOTE that this is a static function. To call it, use;
// TH1::AddDirectory
fgAddDirectory = add;
}
//______________________________________________________________________________
Int_t TH1::BufferEmpty(Int_t action)
{
// Fill histogram with all entries in the buffer.
// action = -1 histogram is reset and refilled from the buffer (called by THistPainter::Paint)
// action = 0 histogram is filled from the buffer
// action = 1 histogram is filled and buffer is deleted
// The buffer is automatically deleted when the number of entries
// in the buffer is greater than the number of entries in the histogram
// do we need to compute the bin size?
if (!fBuffer) return 0;
Int_t nbentries = (Int_t)fBuffer[0];
if (!nbentries) return 0;
Double_t *buffer = fBuffer;
if (nbentries < 0) {
if (action == 0) return 0;
nbentries = -nbentries;
fBuffer=0;
Reset();
fBuffer = buffer;
}
if (TestBit(kCanRebin) || (fXaxis.GetXmax() <= fXaxis.GetXmin())) {
//find min, max of entries in buffer
Double_t xmin = fBuffer[2];
Double_t xmax = xmin;
for (Int_t i=1;i<nbentries;i++) {
Double_t x = fBuffer[2*i+2];
if (x < xmin) xmin = x;
if (x > xmax) xmax = x;
}
if (fXaxis.GetXmax() <= fXaxis.GetXmin()) {
THLimitsFinder::GetLimitsFinder()->FindGoodLimits(this,xmin,xmax);
} else {
fBuffer = 0;
Int_t keep = fBufferSize; fBufferSize = 0;
if (xmin < fXaxis.GetXmin()) RebinAxis(xmin,"X");
if (xmax >= fXaxis.GetXmax()) RebinAxis(xmax,"X");
fBuffer = buffer;
fBufferSize = keep;
}
}
FillN(nbentries,&fBuffer[2],&fBuffer[1],2);
if (action > 0) { delete [] fBuffer; fBuffer = 0; fBufferSize = 0;}
else {
if (nbentries == (Int_t)fEntries) fBuffer[0] = -nbentries;
else fBuffer[0] = 0;
}
return nbentries;
}
//______________________________________________________________________________
Int_t TH1::BufferFill(Axis_t x, Stat_t w)
{
// accumulate arguments in buffer. When buffer is full, empty the buffer
// fBuffer[0] = number of entries in buffer
// fBuffer[1] = w of first entry
// fBuffer[2] = x of first entry
if (!fBuffer) return -2;
Int_t nbentries = (Int_t)fBuffer[0];
if (nbentries < 0) {
nbentries = -nbentries;
fBuffer[0] = nbentries;
if (fEntries > 0) {
Double_t *buffer = fBuffer; fBuffer=0;
Reset();
fBuffer = buffer;
}
}
if (2*nbentries+2 >= fBufferSize) {
BufferEmpty(1);
return Fill(x,w);
}
fBuffer[2*nbentries+1] = w;
fBuffer[2*nbentries+2] = x;
fBuffer[0] += 1;
return -2;
}
//______________________________________________________________________________
Double_t TH1::Chi2Test(const TH1 *h, Option_t *option, Int_t constraint) const
{
//The Chi2 (Pearson's) test for differences between h and this histogram.
//a small value of prob indicates a significant difference between the distributions
//
//if the data was collected in such a way that the number of entries
//in the first histogram is necessarily equal to the number of entries
//in the second, the parameter _constraint_ must be made 1. Default is 0.
//any additional constraints on the data lower the number of degrees of freedom
//(i.e. increase constraint to more positive values) in accordance with
//their number
//
///options:
// "O" : overflows included
// "U" : underflows included
// by default underflows and overflows are not included
//
// "P" : print information about number of degrees of freedom and the value of chi2
// "Chi2" : the function returns the Chisquare instead of the probability
// "Chi2/ndf" : the function returns the Chi2/ndf
// if none of the options "Chi2" or "Chi2/ndf" is specified, the function returns
// the Pearson test, ie probability.
//
// algorithm taken from "Numerical Recipes in C++"
// implementation by Anna Kreshuk
//
// A good description of the Chi2test can be seen at:
// http://www.itl.nist.gov/div898/handbook/eda/section3/eda35f.htm
// See also TH1::KolmogorovTest (including NOTE2)
Int_t i, i_start, i_end;
TString opt = option;
opt.ToUpper();
TAxis *axis1 = this->GetXaxis();
TAxis *axis2 = h->GetXaxis();
Int_t nbins1 = axis1->GetNbins();
Int_t nbins2 = axis2->GetNbins();
//check dimensions
if (this->GetDimension()!=1 || h->GetDimension()!=1){
Error("Chi2Test","for 1-d only");
return 0;
}
//check number of channels
if (nbins1 != nbins2){
Error("Chi2Test","different number of channels");
return 0;
}
//see options
i_start = 1;
i_end = nbins1;
Int_t ndf = nbins1-constraint;
if(opt.Contains("O")) {
i_end = nbins1+1;
ndf++;
}
if(opt.Contains("U")) {
i_start = 0;
ndf++;
}
//Compute the normalisation factor
Double_t sum1=0, sum2=0;
for (i=i_start; i<=i_end; i++){
sum1 += this->GetBinContent(i);
sum2 += h->GetBinContent(i);
}
//check that the histograms are not empty
if (sum1 == 0 || sum2 == 0){
Error("Chi2Test","one of the histograms is empty");
return 0;
}
Double_t chsq = 0;
Double_t bin1, bin2, err1, err2, temp;
for (i=i_start; i<=i_end; i++){
bin1 = this->GetBinContent(i)/sum1;
bin2 = h->GetBinContent(i)/sum2;
if (bin1 ==0 && bin2==0){
--ndf; //no data means one less degree of freedom
} else {
temp = bin1-bin2;
err1=this->GetBinError(i);
err2=h->GetBinError(i);
if (err1 == 0 && err2 == 0){
Error("Chi2Test", "bins with non-zero content and zero error");
return 0;
}
err1*=err1;
err2*=err2;
err1/=sum1*sum1;
err2/=sum2*sum2;
chsq+=temp*temp/(err1+err2);
}
}
Double_t prob = TMath::Prob(0.5*chsq, Int_t(0.5*ndf));
if (opt.Contains("P")){
Printf("Chi2 = %f, Prob = %g, NDF = %d\n", chsq,prob,ndf);
}
if (opt.Contains("CHI2/NDF")){
if (ndf == 0) return 0;
return chsq/ndf;
}
if (opt.Contains("CHI2")){
return chsq;
}
return prob;
}
//______________________________________________________________________________
Double_t TH1::ComputeIntegral()
{
// Compute integral (cumulative sum of bins)
// The result stored in fIntegral is used by the GetRandom functions.
// This function is automatically called by GetRandom when the fIntegral
// array does not exist or when the number of entries in the histogram
// has changed since the previous call to GetRandom.
// The resulting integral is normalized to 1
Int_t bin, binx, biny, binz, ibin;
// delete previously computed integral (if any)
if (fIntegral) delete [] fIntegral;
// - Allocate space to store the integral and compute integral
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
Int_t nxy = nbinsx*nbinsy;
Int_t nbins = nxy*nbinsz;
fIntegral = new Double_t[nbins+2];
ibin = 0;
fIntegral[ibin] = 0;
for (binz=1;binz<=nbinsz;binz++) {
for (biny=1;biny<=nbinsy;biny++) {
for (binx=1;binx<=nbinsx;binx++) {
ibin++;
bin = GetBin(binx, biny, binz);
fIntegral[ibin] = fIntegral[ibin-1] + GetBinContent(bin);
}
}
}
// - Normalize integral to 1
if (fIntegral[nbins] == 0 ) {
Error("ComputeIntegral", "Integral = zero"); return 0;
}
for (bin=1;bin<=nbins;bin++) fIntegral[bin] /= fIntegral[nbins];
fIntegral[nbins+1] = fEntries;
return fIntegral[nbins];
}
//______________________________________________________________________________
Double_t *TH1::GetIntegral()
{
// Return a pointer to the array of bins integral.
// if the pointer fIntegral is null, TH1::ComputeIntegral is called
if (fIntegral) ComputeIntegral();
return fIntegral;
}
//______________________________________________________________________________
void TH1::Copy(TObject &obj) const
{
// -*-*-*-*-*Copy this histogram structure to newth1*-*-*-*-*-*-*-*-*-*-*-*
// =======================================
//
// Note that this function does not copy the list of associated functions.
// Use TObJect::Clone to make a full copy of an histogram.
if (((TH1&)obj).fDirectory) {
// We are likely to change the hash value of this object
// with TNamed::Copy, to keep things correct, we need to
// clean up its existing entries.
((TH1&)obj).fDirectory->GetList()->Remove(&obj);
((TH1&)obj).fDirectory = 0;
}
TNamed::Copy(obj);
((TH1&)obj).fDimension = fDimension;
((TH1&)obj).fNormFactor= fNormFactor;
((TH1&)obj).fEntries = fEntries;
((TH1&)obj).fNcells = fNcells;
((TH1&)obj).fBarOffset = fBarOffset;
((TH1&)obj).fBarWidth = fBarWidth;
((TH1&)obj).fTsumw = fTsumw;
((TH1&)obj).fTsumw2 = fTsumw2;
((TH1&)obj).fTsumwx = fTsumwx;
((TH1&)obj).fTsumwx2 = fTsumwx2;
((TH1&)obj).fMaximum = fMaximum;
((TH1&)obj).fMinimum = fMinimum;
((TH1&)obj).fOption = fOption;
((TH1&)obj).fBuffer = 0;
((TH1&)obj).fBufferSize= fBufferSize;
if (fBuffer) {
Double_t *buf = new Double_t[fBufferSize];
for (Int_t i=0;i<fBufferSize;i++) buf[i] = fBuffer[i];
((TH1&)obj).fBuffer = buf;
}
TAttLine::Copy(((TH1&)obj));
TAttFill::Copy(((TH1&)obj));
TAttMarker::Copy(((TH1&)obj));
fXaxis.Copy(((TH1&)obj).fXaxis);
fYaxis.Copy(((TH1&)obj).fYaxis);
fZaxis.Copy(((TH1&)obj).fZaxis);
((TH1&)obj).fXaxis.SetParent(&obj);
((TH1&)obj).fYaxis.SetParent(&obj);
((TH1&)obj).fZaxis.SetParent(&obj);
fContour.Copy(((TH1&)obj).fContour);
fSumw2.Copy(((TH1&)obj).fSumw2);
// fFunctions->Copy(((TH1&)obj).fFunctions);
if (fgAddDirectory && gDirectory) {
gDirectory->Append(&obj);
((TH1&)obj).fDirectory = gDirectory;
}
}
//______________________________________________________________________________
Int_t TH1::DistancetoPrimitive(Int_t px, Int_t py)
{
// -*-*-*-*-*-*-*-*-*Compute distance from point px,py to a line*-*-*-*-*-*
// ===========================================
// Compute the closest distance of approach from point px,py to elements
// of an histogram.
// The distance is computed in pixels units.
//
// Algorithm:
// Currently, this simple model computes the distance from the mouse
// to the histogram contour only.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (!fPainter) return 9999;
return fPainter->DistancetoPrimitive(px,py);
}
//______________________________________________________________________________
void TH1::Divide(TF1 *f1, Double_t c1)
{
// Performs the operation: this = this/(c1*f1)
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
//
// Only bins inside the function range are recomputed.
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Divide
if (!f1) {
Error("Add","Attempt to divide by a non-existing function");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// - Add statistics
Double_t nEntries = fEntries;
Stat_t s1[10];
Int_t i;
for (i=0;i<10;i++) {s1[i] = 0;}
PutStats(s1);
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu,w;
Double_t xx[3];
Double_t *params = 0;
f1->InitArgs(xx,params);
for (binz=0;binz<=nbinsz+1;binz++) {
xx[2] = fZaxis.GetBinCenter(binz);
for (biny=0;biny<=nbinsy+1;biny++) {
xx[1] = fYaxis.GetBinCenter(biny);
for (binx=0;binx<=nbinsx+1;binx++) {
xx[0] = fXaxis.GetBinCenter(binx);
if (!f1->IsInside(xx)) continue;
TF1::RejectPoint(kFALSE);
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
Double_t error1 = GetBinError(bin);
cu = c1*f1->EvalPar(xx);
if (TF1::RejectedPoint()) continue;
if (cu) w = GetBinContent(bin)/cu;
else w = 0;
SetBinContent(bin,w);
if (fSumw2.fN) {
if (cu != 0) fSumw2.fArray[bin] = error1*error1/(cu*cu);
else fSumw2.fArray[bin] = 0;
}
}
}
}
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Divide(const TH1 *h1)
{
// -*-*-*-*-*-*-*-*-*Divide this histogram by h1*-*-*-*-*-*-*-*-*-*-*-*-*
// ===========================
//
// this = this/h1
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
// Note that if h1 has Sumw2 set, Sumw2 is automatically called for this
// if not already set.
// The resulting errors are calculated assuming uncorrelated histograms.
// See the other TH1::Divide that gives the possibility to optionaly
// compute Binomial errors.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Scale
if (!h1) {
Error("Divide","Attempt to divide by a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()) {
Error("Divide","Attempt to divide histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Divide","Attempt to divide histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 has Sumw2 set
if (fSumw2.fN == 0 && h1->GetSumw2N() != 0) Sumw2();
// - Reset statistics
Double_t nEntries = fEntries;
fEntries = fTsumw = 0;
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t c0,c1,w;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = GetBin(binx,biny,binz);
c0 = GetBinContent(bin);
c1 = h1->GetBinContent(bin);
if (c1) w = c0/c1;
else w = 0;
SetBinContent(bin,w);
fEntries++;
if (fSumw2.fN) {
Double_t e0 = GetBinError(bin);
Double_t e1 = h1->GetBinError(bin);
Double_t c12= c1*c1;
if (!c1) { fSumw2.fArray[bin] = 0; continue;}
fSumw2.fArray[bin] = (e0*e0*c1*c1 + e1*e1*c0*c0)/(c12*c12);
}
}
}
}
Stat_t s[kNstat];
GetStats(s);
PutStats(s);
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Divide(const TH1 *h1, const TH1 *h2, Double_t c1, Double_t c2, Option_t *option)
{
// -*-*-*Replace contents of this histogram by the division of h1 by h2*-*-*
// ==============================================================
//
// this = c1*h1/(c2*h2)
//
// if errors are defined (see TH1::Sumw2), errors are also recalculated
// Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this
// if not already set.
// The resulting errors are calculated assuming uncorrelated histograms.
// However, if option ="B" is specified, Binomial errors are computed.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Divide
TString opt = option;
opt.ToLower();
Bool_t binomial = kFALSE;
if (opt.Contains("b")) binomial = kTRUE;
if (!h1 || !h2) {
Error("Divide","Attempt to divide by a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()
|| nbinsx != h2->GetNbinsX() || nbinsy != h2->GetNbinsY() || nbinsz != h2->GetNbinsZ()) {
Error("Divide","Attempt to divide histograms with different number of bins");
return;
}
if (!c2) {
Error("Divide","Coefficient of dividing histogram cannot be zero");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Divide","Attempt to divide histograms with different axis limits");
}
if (fXaxis.GetXmin() != h2->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h2->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h2->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h2->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h2->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h2->fZaxis.GetXmax()) {
Warning("Divide","Attempt to divide histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 or h2 have Sumw2 set
if (fSumw2.fN == 0 && (h1->GetSumw2N() != 0 || h2->GetSumw2N() != 0)) Sumw2();
// - Reset statistics
Double_t nEntries = fEntries;
fEntries = fTsumw = 0;
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t b1,b2,w,d1,d2;
d1 = c1*c1;
d2 = c2*c2;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
b1 = h1->GetBinContent(bin);
b2 = h2->GetBinContent(bin);
if (b2) w = c1*b1/(c2*b2);
else w = 0;
SetBinContent(bin,w);
fEntries++;
if (fSumw2.fN) {
Double_t e1 = h1->GetBinError(bin);
Double_t e2 = h2->GetBinError(bin);
Double_t b22= b2*b2*d2;
if (!b2) { fSumw2.fArray[bin] = 0; continue;}
if (binomial) {
if (b1 != b2) {
//fSumw2.fArray[bin] = TMath::Abs(w*(1-w)/(c2*b2));//this is the formula in Hbook/Hoper1
fSumw2.fArray[bin] = TMath::Abs(w*(1-w)/b2);
} else {
//in case b1=b2 use a simplification of the special algorithm
//from TGraphAsymmErrors::BayesDivide calling Efficiency, etc
Double_t too_low = 0;
Double_t too_high = 1;
Double_t integral;
Double_t a = b1+1;
Double_t x;
for (Int_t loop=0; loop<20; loop++) {
x = 0.5*(too_high + too_low);
Double_t bt = TMath::Exp(TMath::LnGamma(a+1)-TMath::LnGamma(a)+a*log(x)+log(1-x));
if (x < (a+1.0)/(a+3.0)) integral = 1 - bt*TMath::BetaCf(x,a,1)/a;
else integral = bt*TMath::BetaCf(1-x,1,a);
if (integral > 0.683) too_low = x;
else too_high = x;
}
fSumw2.fArray[bin] = (1-x)*(1-x)/4;
}
} else {
fSumw2.fArray[bin] = d1*d2*(e1*e1*b2*b2 + e2*e2*b1*b1)/(b22*b22);
}
}
}
}
}
Stat_t s[kNstat];
GetStats(s);
PutStats(s);
if (nEntries == 0) nEntries = h1->GetEntries();
if (nEntries == 0) nEntries = 1;
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Draw(Option_t *option)
{
// -*-*-*-*-*-*-*-*-*Draw this histogram with options*-*-*-*-*-*-*-*-*-*-*-*
// ================================
//
// Histograms are drawn via the THistPainter class. Each histogram has
// a pointer to its own painter (to be usable in a multithreaded program).
// The same histogram can be drawn with different options in different pads.
// When an histogram drawn in a pad is deleted, the histogram is
// automatically removed from the pad or pads where it was drawn.
// If an histogram is drawn in a pad, then filled again, the new status
// of the histogram will be automatically shown in the pad next time
// the pad is updated. One does not need to redraw the histogram.
// To draw the current version of an histogram in a pad, one can use
// h->DrawCopy();
// This makes a clone of the histogram. Once the clone is drawn, the original
// histogram may be modified or deleted without affecting the aspect of the
// clone.
// By default, TH1::Draw clears the current pad.
//
// One can use TH1::SetMaximum and TH1::SetMinimum to force a particular
// value for the maximum or the minimum scale on the plot.
//
// TH1::UseCurrentStyle can be used to change all histogram graphics
// attributes to correspond to the current selected style.
// This function must be called for each histogram.
// In case one reads and draws many histograms from a file, one can force
// the histograms to inherit automatically the current graphics style
// by calling before gROOT->ForceStyle();
//
// See THistPainter::Paint for a description of all the drawing options
// =======================
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TString opt = option;
opt.ToLower();
if (gPad) {
if (!gPad->IsEditable()) (gROOT->GetMakeDefCanvas())();
if (!opt.Contains("same")) {
//the following statement is necessary in case one attempts to draw
//a temporary histogram already in the current pad
if (TestBit(kCanDelete)) gPad->GetListOfPrimitives()->Remove(this);
gPad->Clear();
}
}
AppendPad(opt.Data());
}
//______________________________________________________________________________
TH1 *TH1::DrawCopy(Option_t *) const
{
// -*-*-*-*-*Copy this histogram and Draw in the current pad*-*-*-*-*-*-*-*
// ===============================================
//
// Once the histogram is drawn into the pad, any further modification
// using graphics input will be made on the copy of the histogram,
// and not to the original object.
//
// See Draw for the list of options
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
AbstractMethod("DrawCopy");
return 0;
}
//______________________________________________________________________________
TH1 *TH1::DrawNormalized(Option_t *option, Double_t norm) const
{
// Draw a normalized copy of this histogram.
//
// A clone of this histogram is normalized to norm and drawn with option.
// A pointer to the normalized histogram is returned.
// The contents of the histogram copy are scaled such that the new
// sum of weights (excluding under and overflow) is equal to norm.
// Note that the returned normalized histogram is not added to the list
// of histograms in the current directory in memory.
// It is the user's responsability to delete this histogram.
// The kCanDelete bit is set for the returned object. If a pad containing
// this copy is cleared, the histogram will be automatically deleted.
//
// See Draw for the list of options
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Double_t sum = GetSumOfWeights();
if (sum == 0) {
Error("DrawNormalized","Sum of weights is null. Cannot normalized histogram: %s",GetName());
return 0;
}
Bool_t addStatus = TH1::AddDirectoryStatus();
TH1::AddDirectory(kFALSE);
TH1 *h = (TH1*)Clone();
h->SetBit(kCanDelete);
h->Scale(norm/sum);
h->Draw(option);
TH1::AddDirectory(addStatus);
return h;
}
//______________________________________________________________________________
void TH1::DrawPanel()
{
// -*-*-*-*-*Display a panel with all histogram drawing options*-*-*-*-*-*
// ==================================================
//
// See class TDrawPanelHist for example
if (!fPainter) {Draw(); if (gPad) gPad->Update();}
if (fPainter) fPainter->DrawPanel();
}
//______________________________________________________________________________
void TH1::Eval(TF1 *f1, Option_t *option)
{
// -*-*-*Evaluate function f1 at the center of bins of this histogram-*-*-*-*
// ============================================================
//
// If option "R" is specified, the function is evaluated only
// for the bins included in the function range.
// If option "A" is specified, the value of the function is added to the
// existing bin contents
// If option "S" is specified, the value of the function is used to
// generate a value, distributed according to the Poisson
// distribution, with f1 as the mean.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Double_t x[3];
Int_t range,stat,add,bin,binx,biny,binz,nbinsx, nbinsy, nbinsz;
if (!f1) return;
Double_t fu;
Double_t e=0;
TString opt = option;
opt.ToLower();
if (opt.Contains("a")) add = 1;
else add = 0;
if (opt.Contains("s")) stat = 1;
else stat = 0;
if (opt.Contains("r")) range = 1;
else range = 0;
nbinsx = fXaxis.GetNbins();
nbinsy = fYaxis.GetNbins();
nbinsz = fZaxis.GetNbins();
if (!add) Reset();
for (binz=1;binz<=nbinsz;binz++) {
x[2] = fZaxis.GetBinCenter(binz);
for (biny=1;biny<=nbinsy;biny++) {
x[1] = fYaxis.GetBinCenter(biny);
for (binx=1;binx<=nbinsx;binx++) {
bin = GetBin(binx,biny,binz);
x[0] = fXaxis.GetBinCenter(binx);
if (range && !f1->IsInside(x)) continue;
fu = f1->Eval(x[0],x[1],x[2]);
if (stat) fu = gRandom->PoissonD(fu);
if (fSumw2.fN) e = fSumw2.fArray[bin];
AddBinContent(bin,fu);
if (fSumw2.fN) fSumw2.fArray[bin] = e+ TMath::Abs(fu);
}
}
}
}
//______________________________________________________________________________
void TH1::ExecuteEvent(Int_t event, Int_t px, Int_t py)
{
// -*-*-*-*-*-*-*-*-*Execute action corresponding to one event*-*-*-*
// =========================================
// This member function is called when a histogram is clicked with the locator
//
// If Left button clicked on the bin top value, then the content of this bin
// is modified according to the new position of the mouse when it is released.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (fPainter) fPainter->ExecuteEvent(event, px, py);
}
//______________________________________________________________________________
Int_t TH1::Fill(Axis_t x)
{
// -*-*-*-*-*-*-*-*Increment bin with abscissa X by 1*-*-*-*-*-*-*-*-*-*-*
// ==================================
//
// if x is less than the low-edge of the first bin, the Underflow bin is incremented
// if x is greater than the upper edge of last bin, the Overflow bin is incremented
//
// If the storage of the sum of squares of weights has been triggered,
// via the function Sumw2, then the sum of the squares of weights is incremented
// by 1 in the bin corresponding to x.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (fBuffer) return BufferFill(x,1);
Int_t bin;
fEntries++;
bin =fXaxis.FindBin(x);
AddBinContent(bin);
if (fSumw2.fN) ++fSumw2.fArray[bin];
if (bin == 0 || bin > fXaxis.GetNbins()) {
if (!fgStatOverflows) return -1;
}
++fTsumw;
++fTsumw2;
fTsumwx += x;
fTsumwx2 += x*x;
return bin;
}
//______________________________________________________________________________
Int_t TH1::Fill(Axis_t x, Stat_t w)
{
// -*-*-*-*-*-*Increment bin with abscissa X with a weight w*-*-*-*-*-*-*-*
// =============================================
//
// if x is less than the low-edge of the first bin, the Underflow bin is incremented
// if x is greater than the upper edge of last bin, the Overflow bin is incremented
//
// If the storage of the sum of squares of weights has been triggered,
// via the function Sumw2, then the sum of the squares of weights is incremented
// by w^2 in the bin corresponding to x.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (fBuffer) return BufferFill(x,w);
Int_t bin;
fEntries++;
bin =fXaxis.FindBin(x);
AddBinContent(bin, w);
if (fSumw2.fN) fSumw2.fArray[bin] += w*w;
if (bin == 0 || bin > fXaxis.GetNbins()) {
if (!fgStatOverflows) return -1;
}
Stat_t z= (w > 0 ? w : -w);
fTsumw += z;
fTsumw2 += z*z;
fTsumwx += z*x;
fTsumwx2 += z*x*x;
return bin;
}
//______________________________________________________________________________
Int_t TH1::Fill(const char *namex, Stat_t w)
{
// Increment bin with namex with a weight w
//
// if x is less than the low-edge of the first bin, the Underflow bin is incremented
// if x is greater than the upper edge of last bin, the Overflow bin is incremented
//
// If the storage of the sum of squares of weights has been triggered,
// via the function Sumw2, then the sum of the squares of weights is incremented
// by w^2 in the bin corresponding to x.
//
Int_t bin;
fEntries++;
bin =fXaxis.FindBin(namex);
AddBinContent(bin, w);
if (fSumw2.fN) fSumw2.fArray[bin] += w*w;
if (bin == 0 || bin > fXaxis.GetNbins()) return -1;
Axis_t x = fXaxis.GetBinCenter(bin);
Stat_t z= (w > 0 ? w : -w);
fTsumw += z;
fTsumw2 += z*z;
fTsumwx += z*x;
fTsumwx2 += z*x*x;
return bin;
}
//______________________________________________________________________________
void TH1::FillN(Int_t ntimes, const Axis_t *x, const Double_t *w, Int_t stride)
{
// -*-*-*-*-*-*Fill this histogram with an array x and weights w*-*-*-*-*
// =================================================
//
// ntimes: number of entries in arrays x and w (array size must be ntimes*stride)
// x: array of values to be histogrammed
// w: array of weighs
// stride: step size through arrays x and w
//
// If the storage of the sum of squares of weights has been triggered,
// via the function Sumw2, then the sum of the squares of weights is incremented
// by w[i]^2 in the bin corresponding to x[i].
// if w is NULL each entry is assumed a weight=1
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t bin,i;
fEntries += ntimes;
Double_t ww = 1;
Int_t nbins = fXaxis.GetNbins();
ntimes *= stride;
for (i=0;i<ntimes;i+=stride) {
bin =fXaxis.FindBin(x[i]);
if (w) ww = w[i];
AddBinContent(bin, ww);
if (fSumw2.fN) fSumw2.fArray[bin] += ww*ww;
if (bin == 0 || bin > nbins) {
if (!fgStatOverflows) continue;
}
Stat_t z= (ww > 0 ? ww : -ww);
fTsumw += z;
fTsumw2 += z*z;
fTsumwx += z*x[i];
fTsumwx2 += z*x[i]*x[i];
}
}
//______________________________________________________________________________
void TH1::FillRandom(const char *fname, Int_t ntimes)
{
// -*-*-*-*-*Fill histogram following distribution in function fname*-*-*-*
// =======================================================
//
// The distribution contained in the function fname (TF1) is integrated
// over the channel contents.
// It is normalized to 1.
// Getting one random number implies:
// - Generating a random number between 0 and 1 (say r1)
// - Look in which bin in the normalized integral r1 corresponds to
// - Fill histogram channel
// ntimes random numbers are generated
//
// One can also call TF1::GetRandom to get a random variate from a function.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-**-*-*-*-*-*-*-*
Int_t bin, binx, ibin, loop;
Double_t r1, x, xv[1];
// - Search for fname in the list of ROOT defined functions
TF1 *f1 = (TF1*)gROOT->GetFunction(fname);
if (!f1) { Error("FillRandom", "Unknown function: %s",fname); return; }
// - Allocate temporary space to store the integral and compute integral
Int_t nbinsx = GetNbinsX();
Double_t *integral = new Double_t[nbinsx+1];
ibin = 0;
integral[ibin] = 0;
for (binx=1;binx<=nbinsx;binx++) {
xv[0] = fXaxis.GetBinCenter(binx);
ibin++;
Double_t fval = f1->Eval(xv[0]);
integral[ibin] = integral[ibin-1] + TMath::Abs(fval)*fXaxis.GetBinWidth(binx);
}
// - Normalize integral to 1
if (integral[nbinsx] == 0 ) {
Error("FillRandom", "Integral = zero"); return;
}
for (bin=1;bin<=nbinsx;bin++) integral[bin] /= integral[nbinsx];
// --------------Start main loop ntimes
for (loop=0;loop<ntimes;loop++) {
r1 = gRandom->Rndm(loop);
ibin = TMath::BinarySearch(nbinsx,&integral[0],r1);
binx = 1 + ibin;
//x = fXaxis.GetBinCenter(binx); //this is not OK when SetBuffer is used
x = fXaxis.GetBinLowEdge(ibin+1)
+fXaxis.GetBinWidth(ibin+1)*(r1-integral[ibin])/(integral[ibin+1] - integral[ibin]);
Fill(x, 1.);
}
delete [] integral;
}
//______________________________________________________________________________
void TH1::FillRandom(TH1 *h, Int_t ntimes)
{
// -*-*-*-*-*Fill histogram following distribution in histogram h*-*-*-*
// ====================================================
//
// The distribution contained in the histogram h (TH1) is integrated
// over the channel contents.
// It is normalized to 1.
// Getting one random number implies:
// - Generating a random number between 0 and 1 (say r1)
// - Look in which bin in the normalized integral r1 corresponds to
// - Fill histogram channel
// ntimes random numbers are generated
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-**-*-*-*-*-*-*-*
if (!h) { Error("FillRandom", "Null histogram"); return; }
if (fDimension != h->GetDimension()) {
Error("FillRandom", "Histograms with different dimensions"); return;
}
if (h->ComputeIntegral() == 0) return;
Int_t loop;
Axis_t x;
for (loop=0;loop<ntimes;loop++) {
x = h->GetRandom();
Fill(x);
}
}
//______________________________________________________________________________
Int_t TH1::FindBin(Axis_t x, Axis_t y, Axis_t z)
{
// -*-*-*-*Return Global bin number corresponding to x,y,z*-*-*-*-*-*-*
// ===============================================
//
// 2-D and 3-D histograms are represented with a one dimensional
// structure.
// This has the advantage that all existing functions, such as
// GetBinContent, GetBinError, GetBinFunction work for all dimensions.
// See also TH1::GetBin
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (GetDimension() < 2) {
return fXaxis.FindBin(x);
}
if (GetDimension() < 3) {
Int_t nx = fXaxis.GetNbins()+2;
Int_t binx = fXaxis.FindBin(x);
Int_t biny = fYaxis.FindBin(y);
return binx + nx*biny;
}
if (GetDimension() < 4) {
Int_t nx = fXaxis.GetNbins()+2;
Int_t ny = fYaxis.GetNbins()+2;
Int_t binx = fXaxis.FindBin(x);
Int_t biny = fYaxis.FindBin(y);
Int_t binz = fZaxis.FindBin(z);
return binx + nx*(biny +ny*binz);
}
return -1;
}
//______________________________________________________________________________
TObject *TH1::FindObject(const char *name) const
{
// search object named name in the list of functions
if (fFunctions) return fFunctions->FindObject(name);
return 0;
}
//______________________________________________________________________________
TObject *TH1::FindObject(const TObject *obj) const
{
// search object obj in the list of functions
if (fFunctions) return fFunctions->FindObject(obj);
return 0;
}
//______________________________________________________________________________
Int_t TH1::Fit(const char *fname ,Option_t *option ,Option_t *goption, Axis_t xxmin, Axis_t xxmax)
{
// Fit histogram with function fname
// =================================
// fname is the name of an already predefined function created by TF1 or TF2
// Predefined functions such as gaus, expo and poln are automatically
// created by ROOT.
// fname can also be a formula, accepted by the linear fitter (linear parts divided
// by "++" sign), for example "x++sin(x)" for fitting "[0]*x+[1]*sin(x)"
//
// This function finds a pointer to the TF1 object with name fname
// and calls TH1::Fit(TF1 *f1,...)
char *linear;
linear= (char*)strstr(fname, "++");
TF1 *f1=0;
TF2 *f2=0;
TF3 *f3=0;
Int_t ndim=GetDimension();
if (linear){
if (ndim<2){
f1=new TF1(fname, fname, xxmin, xxmax);
return Fit(f1,option,goption,xxmin,xxmax);
}
else if (ndim<3){
f2=new TF2(fname, fname);
return Fit(f2,option,goption,xxmin,xxmax);
}
else{
f3=new TF3(fname, fname);
return Fit(f3,option,goption,xxmin,xxmax);
}
}
else{
f1 = (TF1*)gROOT->GetFunction(fname);
if (!f1) { Printf("Unknown function: %s",fname); return -1; }
return Fit(f1,option,goption,xxmin,xxmax);
}
}
//______________________________________________________________________________
Int_t TH1::Fit(TF1 *f1 ,Option_t *option ,Option_t *goption, Axis_t xxmin, Axis_t xxmax)
{
// Fit histogram with function f1
// ==============================
//
// Fit this histogram with function f1.
//
// The list of fit options is given in parameter option.
// option = "W" Set all errors to 1
// = "I" Use integral of function in bin instead of value at bin center
// = "L" Use Loglikelihood method (default is chisquare method)
// = "LL" Use Loglikelihood method and bin contents are not integers)
// = "U" Use a User specified fitting algorithm (via SetFCN)
// = "Q" Quiet mode (minimum printing)
// = "V" Verbose mode (default is between Q and V)
// = "E" Perform better Errors estimation using Minos technique
// = "B" Use this option when you want to fix one or more parameters
// and the fitting function is like "gaus","expo","poln","landau".
// = "M" More. Improve fit results
// = "R" Use the Range specified in the function range
// = "N" Do not store the graphics function, do not draw
// = "0" Do not plot the result of the fit. By default the fitted function
// is drawn unless the option"N" above is specified.
// = "+" Add this new fitted function to the list of fitted functions
// (by default, any previous function is deleted)
// = "C" In case of linear fitting, don't calculate the chisquare
// (saves time)
// = "F" If fitting a polN, switch to minuit fitter
//
// When the fit is drawn (by default), the parameter goption may be used
// to specify a list of graphics options. See TH1::Draw for a complete
// list of these options.
//
// In order to use the Range option, one must first create a function
// with the expression to be fitted. For example, if your histogram
// has a defined range between -4 and 4 and you want to fit a gaussian
// only in the interval 1 to 3, you can do:
// TF1 *f1 = new TF1("f1","gaus",1,3);
// histo->Fit("f1","R");
//
// Setting initial conditions
// ==========================
// Parameters must be initialized before invoking the Fit function.
// The setting of the parameter initial values is automatic for the
// predefined functions : poln, expo, gaus, landau. One can however disable
// this automatic computation by specifying the option "B".
// Note that if a predefined function is defined with an argument,
// eg, gaus(0), expo(1), you must specify the initial values for
// the parameters.
// You can specify boundary limits for some or all parameters via
// f1->SetParLimits(p_number, parmin, parmax);
// if parmin>=parmax, the parameter is fixed
// Note that you are not forced to fix the limits for all parameters.
// For example, if you fit a function with 6 parameters, you can do:
// func->SetParameters(0,3.1,1.e-6,-8,0,100);
// func->SetParLimits(3,-10,-4);
// func->FixParameter(4,0);
// func->SetParLimits(5, 1,1);
// With this setup, parameters 0->2 can vary freely
// Parameter 3 has boundaries [-10,-4] with initial value -8
// Parameter 4 is fixed to 0
// Parameter 5 is fixed to 100.
// When the lower limit and upper limit are equal, the parameter is fixed.
// However to fix a parameter to 0, one must call the FixParameter function.
//
// Note that option "I" gives better results but is slower.
//
//
// Changing the fitting function
// =============================
// By default the fitting function H1FitChisquare is used.
// To specify a User defined fitting function, specify option "U" and
// call the following functions:
// TVirtualFitter::Fitter(myhist)->SetFCN(MyFittingFunction)
// where MyFittingFunction is of type:
// extern void MyFittingFunction(Int_t &npar, Double_t *gin, Double_t &f, Double_t *u, Int_t flag);
//
// Associated functions
// ====================
// One or more object (typically a TF1*) can be added to the list
// of functions (fFunctions) associated to each histogram.
// When TH1::Fit is invoked, the fitted function is added to this list.
// Given an histogram h, one can retrieve an associated function
// with: TF1 *myfunc = h->GetFunction("myfunc");
//
// Access to the fit results
// =========================
// If the histogram is made persistent, the list of
// associated functions is also persistent. Given a pointer (see above)
// to an associated function myfunc, one can retrieve the function/fit
// parameters with calls such as:
// Double_t chi2 = myfunc->GetChisquare();
// Double_t par0 = myfunc->GetParameter(0); //value of 1st parameter
// Double_t err0 = myfunc->GetParError(0); //error on first parameter
//
// Access to the fit covariance matrix
// ===================================
// Example1:
// TH1F h("h","test",100,-2,2);
// h.FillRandom("gaus",1000);
// h.Fit("gaus");
// Double_t matrix[3][3];
// gMinuit->mnemat(&matrix[0][0],3);
// Example2:
// TH1F h("h","test",100,-2,2);
// h.FillRandom("gaus",1000);
// h.Fit("gaus");
// TVirtualFitter *fitter = TVirtualFitter::GetFitter();
// TMatrixD matrix(npar,npar,fitter->GetCovarianceMatrix());
// Double_t errorFirstPar = fitter->GetCovarianceMatrixElement(0,0);
//
//
// Changing the maximum number of parameters
// =========================================
// By default, the fitter TMinuit is initialized with a maximum of 25 parameters.
// You can redefine this default value by calling :
// TVirtualFitter::Fitter(0,150); //to get a maximum of 150 parameters
//
// Excluding points
// ================
// Use TF1::RejectPoint inside your fitting function to exclude points
// within a certain range from the fit. Example:
// Double_t fline(Double_t *x, Double_t *par)
// {
// if (x[0] > 2.5 && x[0] < 3.5) {
// TF1::RejectPoint();
// return 0;
// }
// return par[0] + par[1]*x[0];
// }
//
// void exclude() {
// TF1 *f1 = new TF1("f1","[0] +[1]*x +gaus(2)",0,5);
// f1->SetParameters(6,-1,5,3,0.2);
// TH1F *h = new TH1F("h","background + signal",100,0,5);
// h->FillRandom("f1",2000);
// TF1 *fline = new TF1("fline",fline,0,5,2);
// fline->SetParameters(2,-1);
// h->Fit("fline","l");
// }
//
// Warning when using the option "0"
// =================================
// When selecting the option "0", the fitted function is added to
// the list of functions of the histogram, but it is not drawn.
// You can undo what you disabled in the following way:
// h.Fit("myFunction","0"); // fit, store function but do not draw
// h.Draw(); function is not drawn
// const Int_t kNotDraw = 1<<9;
// h.GetFunction("myFunction")->ResetBit(kNotDraw);
// h.Draw(); // function is visible again
//
// Access to the Fitter information during fitting
// ===============================================
// This function calls only the abstract fitter TVirtualFitter.
// The default fitter is TFitter (calls TMinuit).
// The default fitter can be set in the resource file in etc/system.rootrc
// Root.Fitter: Fumili
// A different fitter can also be set via TVirtualFitter::SetDefaultFitter.
// For example, to call the "Fumili" fitter instead of "Minuit", do
// TVirtualFitter::SetDefaultFitter("Fumili");
// During the fitting process, the objective function:
// chisquare, likelihood or any user defined algorithm
// is called (see eg in the TFitter class, the static functions
// H1FitChisquare, H1FitLikelihood).
// This objective function, in turn, calls the user theoretical function.
// This user function is a static function called from the TF1 *f1 function.
// Inside this user defined theoretical function , one can access:
// TVirtualFitter *fitter = TVirtualFitter::GetFitter(); //the current fitter
// TH1 *hist = (TH1*)fitter->GetObjectFit(); //the histogram being fitted
// TF1 +f1 = (TF1*)fitter->GetUserFunction(); //the user theoretical function
//
// By default, the fitter TMinuit is initialized with a maximum of 25 parameters.
// For fitting linear functions (containing the "++" sign" and polN functions,
// the linear fitter is initialized.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t fitResult = 0;
Int_t i, npar,nvpar,nparx;
Double_t par, we, al, bl;
Double_t eplus,eminus,eparab,globcc,amin,aminref,edm,errdef,werr;
Double_t params[100], arglist[100];
Axis_t xmin, xmax, ymin, ymax, zmin, zmax, binwidx, binwidy, binwidz;
Int_t hxfirst, hxlast, hyfirst, hylast, hzfirst, hzlast;
TF1 *fnew1;
TF2 *fnew2;
TF3 *fnew3;
// Check validity of function
if (!f1) {
Error("Fit", "function may not be null pointer");
return 0;
}
if (f1->IsZombie()) {
Error("Fit", "function is zombie");
return 0;
}
npar = f1->GetNpar();
if (npar <= 0) {
Error("Fit", "function %s has illegal number of parameters = %d", f1->GetName(), npar);
return 0;
}
// Check that function has same dimension as histogram
if (f1->GetNdim() != GetDimension()) {
Error("Fit","function %s dimension, %d, does not match histogram dimension, %d",
f1->GetName(), f1->GetNdim(), GetDimension());
return 0;
}
hxfirst = fXaxis.GetFirst();
hxlast = fXaxis.GetLast();
binwidx = fXaxis.GetBinWidth(hxlast);
xmin = fXaxis.GetBinLowEdge(hxfirst);
xmax = fXaxis.GetBinLowEdge(hxlast) +binwidx;
hyfirst = fYaxis.GetFirst();
hylast = fYaxis.GetLast();
binwidy = fYaxis.GetBinWidth(hylast);
ymin = fYaxis.GetBinLowEdge(hyfirst);
ymax = fYaxis.GetBinLowEdge(hylast) +binwidy;
hzfirst = fZaxis.GetFirst();
hzlast = fZaxis.GetLast();
binwidz = fZaxis.GetBinWidth(hzlast);
zmin = fZaxis.GetBinLowEdge(hzfirst);
zmax = fZaxis.GetBinLowEdge(hzlast) +binwidz;
// - Decode list of options into fitOption
Foption_t fitOption;
if (!FitOptionsMake(option,fitOption)) return 0;
if (xxmin != xxmax) {
f1->SetRange(xxmin,ymin,zmin,xxmax,ymax,zmax);
fitOption.Range = 1;
}
// - Check if Minuit is initialized and create special functions
Int_t special = f1->GetNumber();
Bool_t linear = f1->IsLinear();
if (special==299+npar)
linear = kTRUE;
if (fitOption.Bound || fitOption.Like || fitOption.Errors || fitOption.Gradient || fitOption.More || fitOption.User|| fitOption.Integral || fitOption.Minuit)
linear = kFALSE;
char l[] ="TLinearFitter";
Int_t strdiff = 0;
Bool_t isSet = kFALSE;
if (TVirtualFitter::GetFitter()){
//Is a fitter already set? Is it linear?
isSet=kTRUE;
strdiff = strcmp(TVirtualFitter::GetFitter()->IsA()->GetName(), l);
}
if (linear){
//
TClass *cl = gROOT->GetClass("TLinearFitter");
if (isSet && strdiff!=0) {
delete TVirtualFitter::GetFitter();
isSet=kFALSE;
}
if (!isSet) {
TVirtualFitter::SetFitter((TVirtualFitter *)cl->New());
}
} else {
if (isSet && strdiff==0){
delete TVirtualFitter::GetFitter();
isSet=kFALSE;
}
if (!isSet)
TVirtualFitter::SetFitter(0);
}
TVirtualFitter *hFitter = TVirtualFitter::Fitter(this, f1->GetNpar());
hFitter->Clear();
// - Get pointer to the function by searching in the list of functions in ROOT
gF1 = f1;
hFitter->SetUserFunc(f1);
if (xxmin != xxmax) f1->SetRange(xxmin,ymin,zmin,xxmax,ymax,zmax);
hFitter->SetFitOption(fitOption);
// - Is a Fit range specified?
Double_t fxmin, fymin, fzmin, fxmax, fymax, fzmax;
if (fitOption.Range) {
f1->GetRange(fxmin, fymin, fzmin, fxmax, fymax, fzmax);
if (fxmin > xmin) xmin = fxmin;
if (fymin > ymin) ymin = fymin;
if (fzmin > zmin) zmin = fzmin;
if (fxmax < xmax) xmax = fxmax;
if (fymax < ymax) ymax = fymax;
if (fzmax < zmax) zmax = fzmax;
hxfirst = fXaxis.FindFixBin(xmin); if (hxfirst < 1) hxfirst = 1;
hxlast = fXaxis.FindFixBin(xmax); if (hxlast > fXaxis.GetLast()) hxlast = fXaxis.GetLast();
hyfirst = fYaxis.FindFixBin(ymin); if (hyfirst < 1) hyfirst = 1;
hylast = fYaxis.FindFixBin(ymax); if (hylast > fYaxis.GetLast()) hylast = fYaxis.GetLast();
hzfirst = fZaxis.FindFixBin(zmin); if (hzfirst < 1) hzfirst = 1;
hzlast = fZaxis.FindFixBin(zmax); if (hzlast > fZaxis.GetLast()) hzlast = fZaxis.GetLast();
} else {
f1->SetRange(xmin,ymin,zmin,xmax,ymax,zmax);
}
hFitter->SetXfirst(hxfirst); hFitter->SetXlast(hxlast);
hFitter->SetYfirst(hyfirst); hFitter->SetYlast(hylast);
hFitter->SetZfirst(hzfirst); hFitter->SetZlast(hzlast);
if (linear){
hFitter->ExecuteCommand("FitHist", 0, 0);
} else {
// - If case of a predefined function, then compute initial values of parameters
if (fitOption.Bound) special = 0;
if (special == 100) H1InitGaus();
else if (special == 400) H1InitGaus();
else if (special == 200) H1InitExpo();
else if (special == 299+npar) H1InitPolynom();
// - Some initialisations
if (!fitOption.Verbose) {
arglist[0] = -1;
hFitter->ExecuteCommand("SET PRINT", arglist,1);
arglist[0] = 0;
hFitter->ExecuteCommand("SET NOW", arglist,0);
}
// - Set error criterion for chisquare or likelihood methods
// - MINUIT ErrDEF should not be set to 0.5 in case of loglikelihood fit.
// - because the FCN is already multiplied by 2 in H1FitLikelihood
// - if Hoption.User is specified, assume that the user has already set
// - his minimization function via SetFCN.
arglist[0] = TVirtualFitter::GetErrorDef();
if (fitOption.Like) {
hFitter->SetFitMethod("H1FitLikelihood");
} else {
if (!fitOption.User) hFitter->SetFitMethod("H1FitChisquare");
}
hFitter->ExecuteCommand("SET Err",arglist,1);
// - Transfer names and initial values of parameters to Minuit
Int_t nfixed = 0;
for (i=0;i<npar;i++) {
par = f1->GetParameter(i);
f1->GetParLimits(i,al,bl);
if (al*bl != 0 && al >= bl) {
al = bl = 0;
arglist[nfixed] = i+1;
nfixed++;
}
we = 0.1*TMath::Abs(bl-al);
if (we == 0) we = 0.3*TMath::Abs(par);
if (we == 0) we = binwidx;
hFitter->SetParameter(i,f1->GetParName(i),par,we,al,bl);
}
if(nfixed > 0)hFitter->ExecuteCommand("FIX",arglist,nfixed); // Otto
// - Set Gradient
if (fitOption.Gradient) {
if (fitOption.Gradient == 1) arglist[0] = 1;
else arglist[0] = 0;
hFitter->ExecuteCommand("SET GRAD",arglist,1);
}
// - Reset Print level
if (fitOption.Verbose) {
arglist[0] = 0; hFitter->ExecuteCommand("SET PRINT", arglist,1);
}
// - Compute sum of squares of errors in the bin range
Double_t ey, sumw2=0;
for (i=hxfirst;i<=hxlast;i++) {
ey = GetBinError(i);
sumw2 += ey*ey;
}
//
//
// printf("h1: sumw2=%f\n", sumw2);
//
// - Perform minimization
arglist[0] = TVirtualFitter::GetMaxIterations();
arglist[1] = sumw2*TVirtualFitter::GetPrecision();
fitResult = hFitter->ExecuteCommand("MIGRAD",arglist,2);
if (fitResult != 0) {
// Abnormal termination, MIGRAD might not have converged on a
// minimum.
if (!fitOption.Quiet) {
Warning("Fit","Abnormal termination of minimization.");
}
}
if (fitOption.More) {
hFitter->ExecuteCommand("IMPROVE",arglist,0);
}
if (fitOption.Errors) {
hFitter->ExecuteCommand("HESSE",arglist,0);
hFitter->ExecuteCommand("MINOS",arglist,0);
}
// - Get return status
char parName[50];
for (i=0;i<npar;i++) {
hFitter->GetParameter(i,parName, par,we,al,bl);
if (!fitOption.Errors) werr = we;
else {
hFitter->GetErrors(i,eplus,eminus,eparab,globcc);
if (eplus > 0 && eminus < 0) werr = 0.5*(eplus-eminus);
else werr = we;
}
params[i] = par;
f1->SetParameter(i,par);
f1->SetParError(i,werr);
}
hFitter->GetStats(aminref,edm,errdef,nvpar,nparx);
// If Log Likelihood, compute an equivalent chisquare
//if (fitOption.Like) amin = hFitter->Chisquare(npar, params, amin, params, 1);
amin = aminref;
if (fitOption.Like) amin = hFitter->Chisquare(npar, params);
f1->SetChisquare(amin);
f1->SetNDF(f1->GetNumberFitPoints()-npar+nfixed);
}
// - Print final values of parameters.
if (!fitOption.Quiet) {
if (fitOption.Errors) hFitter->PrintResults(4,aminref);
else hFitter->PrintResults(3,aminref);
}
// - Store fitted function in histogram functions list and draw
if (!fitOption.Nostore) {
if (!fitOption.Plus) {
TIter next(fFunctions, kIterBackward);
TObject *obj;
while ((obj = next())) {
if (obj->InheritsFrom(TF1::Class())) {
fFunctions->Remove(obj);
delete obj;
}
}
}
if (GetDimension() < 2) {
fnew1 = new TF1();
f1->Copy(*fnew1);
fFunctions->Add(fnew1);
fnew1->SetParent(this);
fnew1->Save(xmin,xmax,0,0,0,0);
if (fitOption.Nograph) fnew1->SetBit(TF1::kNotDraw);
fnew1->SetBit(TFormula::kNotGlobal);
} else if (GetDimension() < 3) {
fnew2 = new TF2();
f1->Copy(*fnew2);
fFunctions->Add(fnew2);
fnew2->SetParent(this);
fnew2->Save(xmin,xmax,ymin,ymax,0,0);
if (fitOption.Nograph) fnew2->SetBit(TF1::kNotDraw);
fnew2->SetBit(TFormula::kNotGlobal);
} else {
fnew3 = new TF3();
f1->Copy(*fnew3);
fFunctions->Add(fnew3);
fnew3->SetParent(this);
fnew3->SetBit(TFormula::kNotGlobal);
}
if (TestBit(kCanDelete)) return fitResult;
if (!fitOption.Nograph && GetDimension() < 3) Draw(goption);
}
return fitResult;
}
//______________________________________________________________________________
void TH1::FitPanel()
{
// -*-*-*-*-*Display a panel with all histogram fit options*-*-*-*-*-*
// ==============================================
//
// See class TFitPanel for example
if (fPainter) fPainter->FitPanel();
}
//______________________________________________________________________________
TH1 *TH1::GetAsymmetry(TH1* h2, Double_t c2, Double_t dc2)
{
// return an histogram containing the asymmetry of this histogram with h2,
// where the asymmetry is defined as:
//
// Asymmetry = (h1 - h2)/(h1 + h2) where h1 = this
//
// works for 1D, 2D, etc. histograms
// c2 is an optional argument that gives a relative weight between the two
// histograms, and dc2 is the error on this weight. This is useful, for example,
// when forming an asymmetry between two histograms from 2 different data sets that
// need to be normalized to each other in some way. The function calculates
// the errors asumming Poisson statistics on h1 and h2 (that is, dh = sqrt(h)).
//
// example: assuming 'h1' and 'h2' are already filled
//
// h3 = h1->GetAsymmetry(h2)
//
// then 'h3' is created and filled with the asymmetry between 'h1' and 'h2';
// h1 and h2 are left intact.
//
// Note that it is the user's responsibility to manage the created histogram.
//
// code proposed by Jason Seely (seely@mit.edu) and adapted by R.Brun
//
// clone the histograms so top and bottom will have the
// correct dimensions:
// Sumw2 just makes sure the errors will be computed properly
// when we form sums and ratios below.
Bool_t addStatus = TH1::AddDirectoryStatus();
TH1::AddDirectory(kFALSE);
TH1 *asym = (TH1*)Clone();
asym->Sumw2();
TH1 *top = (TH1*)asym->Clone();
TH1 *bottom = (TH1*)asym->Clone();
TH1::AddDirectory(addStatus);
// form the top and bottom of the asymmetry, and then divide:
TH1 *h1 = this;
top->Add(h1,h2,1,-c2);
bottom->Add(h1,h2,1,c2);
asym->Divide(top,bottom);
Int_t xmax = asym->GetNbinsX();
Int_t ymax = asym->GetNbinsY();
Int_t zmax = asym->GetNbinsZ();
Double_t bot, error, a, b, da, db;
// now loop over bins to calculate the correct errors
// the reason this error calculation looks complex is because of c2
for(Int_t i=1; i<= xmax; i++){
for(Int_t j=1; j<= ymax; j++){
for(Int_t k=1; k<= zmax; k++){
// here some bin contents are written into variables to make the error
// calculation a little more legible:
a = h1->GetBinContent(i,j,k);
b = h2->GetBinContent(i,j,k);
bot = bottom->GetBinContent(i,j,k);
// make sure there are some events, if not, then the errors are set = 0
// automatically.
if(bot < 1){}
else{
// computation of errors by Christos Leonidopoulos
da = h1->GetBinError(i,j,k);
db = h2->GetBinError(i,j,k);
error = 2*TMath::Sqrt(a*a*c2*c2*db*db + c2*c2*b*b*da*da+a*a*b*b*dc2*dc2)/(bot*bot);
asym->SetBinError(i,j,k,error);
}
}
}
}
delete top;
delete bottom;
return asym;
}
//______________________________________________________________________________
Int_t TH1::GetDefaultBufferSize()
{
// return the default buffer size for automatic histograms
// the parameter fgBufferSize may be changed via SetDefaultBufferSize
return fgBufferSize;
}
//______________________________________________________________________________
Double_t TH1::GetEntries() const
{
// return the current number of entries
if (fBuffer) ((TH1*)this)->BufferEmpty();
return fEntries;
}
//______________________________________________________________________________
char *TH1::GetObjectInfo(Int_t px, Int_t py) const
{
// Redefines TObject::GetObjectInfo.
// Displays the histogram info (bin number, contents, integral up to bin
// corresponding to cursor position px,py
//
return ((TH1*)this)->GetPainter()->GetObjectInfo(px,py);
}
//______________________________________________________________________________
TVirtualHistPainter *TH1::GetPainter()
{
// return pointer to painter
// if painter does not exist, it is created
if (!fPainter) fPainter = TVirtualHistPainter::HistPainter(this);
return fPainter;
}
//______________________________________________________________________________
Int_t TH1::GetQuantiles(Int_t nprobSum, Double_t *q, const Double_t *probSum)
{
// Compute Quantiles for this histogram
// Quantile x_q of a probability distribution Function F is defined as
//
// F(x_q) = q with 0 <= q <= 1.
//
// For instance the median x_0.5 of a distribution is defined as that value
// of the random variable for which the distribution function equals 0.5:
//
// F(x_0.5) = Probability(x < x_0.5) = 0.5
//
// code from Eddy Offermann, Renaissance
//
// input parameters
// - this 1-d histogram (TH1F,D,etc). Could also be a TProfile
// - nprobSum maximum size of array q and size of array probSum (if given)
// - probSum array of positions where quantiles will be computed.
// if probSum is null, probSum will be computed internally and will
// have a size = number of bins + 1 in h. it will correspond to the
// quantiles calculated at the lowest edge of the histogram (quantile=0) and
// all the upper edges of the bins.
// if probSum is not null, it is assumed to contain at least nprobSum values.
// output
// - return value nq (<=nprobSum) with the number of quantiles computed
// - array q filled with nq quantiles
//
// Note that the Integral of the histogram is automatically recomputed
// if the number of entries is different of the number of entries when
// the integral was computed last time. In case you do not use the Fill
// functions to fill your histogram, but SetBinContent, you must call
// TH1::ComputeIntegral before calling this function.
//
// Getting quantiles q from two histograms and storing results in a TGraph,
// a so-called QQ-plot
//
// TGraph *gr = new TGraph(nprob);
// h1->GetQuantiles(nprob,gr->GetX());
// h2->GetQuantiles(nprob,gr->GetY());
// gr->Draw("alp");
//
// Example:
// void quantiles() {
// // demo for quantiles
// const Int_t nq = 20;
// TH1F *h = new TH1F("h","demo quantiles",100,-3,3);
// h->FillRandom("gaus",5000);
//
// Double_t xq[nq]; // position where to compute the quantiles in [0,1]
// Double_t yq[nq]; // array to contain the quantiles
// for (Int_t i=0;i<nq;i++) xq[i] = Float_t(i+1)/nq;
// h->GetQuantiles(nq,yq,xq);
//
// //show the original histogram in the top pad
// TCanvas *c1 = new TCanvas("c1","demo quantiles",10,10,700,900);
// c1->Divide(1,2);
// c1->cd(1);
// h->Draw();
//
// // show the quantiles in the bottom pad
// c1->cd(2);
// gPad->SetGrid();
// TGraph *gr = new TGraph(nq,xq,yq);
// gr->SetMarkerStyle(21);
// gr->Draw("alp");
// }
if (GetDimension() > 1) {
Error("GetQuantiles","Only available for 1-d histograms");
return 0;
}
const Int_t nbins = GetXaxis()->GetNbins();
if (!fIntegral) ComputeIntegral();
if (fIntegral && fIntegral[nbins+1] != fEntries) ComputeIntegral();
Int_t i, ibin;
Double_t *prob = (Double_t*)probSum;
Int_t nq = nprobSum;
if (probSum == 0) {
nq = nbins+1;
prob = new Double_t[nq];
prob[0] = 0;
for (i=1;i<nq;i++) {
prob[i] = fIntegral[i]/fIntegral[nbins];
}
}
for (i = 0; i < nq; i++) {
ibin = TMath::BinarySearch(nbins,fIntegral,prob[i]);
while (ibin < nbins-1 && fIntegral[ibin+1] == prob[i]) {
if (fIntegral[ibin+2] == prob[i]) ibin++;
else break;
}
q[i] = GetBinLowEdge(ibin+1);
const Double_t dint = fIntegral[ibin+1]-fIntegral[ibin];
if (dint > 0) q[i] += GetBinWidth(ibin+1)*(prob[i]-fIntegral[ibin])/dint;
}
if (!probSum) delete [] prob;
return nq;
}
//______________________________________________________________________________
Int_t TH1::FitOptionsMake(Option_t *choptin, Foption_t &fitOption)
{
// -*-*-*-*-*-*-*Decode string choptin and fill fitOption structure*-*-*-*-*-*
// ================================================
Int_t nch = strlen(choptin);
if (!nch) return 1;
char chopt[32];
strcpy(chopt,choptin);
for (Int_t i=0;i<nch;i++) chopt[i] = toupper(choptin[i]);
if (strstr(chopt,"Q")) fitOption.Quiet = 1;
if (strstr(chopt,"V")) {fitOption.Verbose = 1; fitOption.Quiet = 0;}
if (strstr(chopt,"L")) fitOption.Like = 1;
if (strstr(chopt,"LL")) fitOption.Like = 2;
if (strstr(chopt,"W")) fitOption.W1 = 1;
if (strstr(chopt,"E")) fitOption.Errors = 1;
if (strstr(chopt,"M")) fitOption.More = 1;
if (strstr(chopt,"R")) fitOption.Range = 1;
if (strstr(chopt,"G")) fitOption.Gradient= 1;
if (strstr(chopt,"N")) fitOption.Nostore = 1;
if (strstr(chopt,"0")) fitOption.Nograph = 1;
if (strstr(chopt,"+")) fitOption.Plus = 1;
if (strstr(chopt,"I")) fitOption.Integral= 1;
if (strstr(chopt,"B")) fitOption.Bound = 1;
if (strstr(chopt,"U")) {fitOption.User = 1; fitOption.Like = 0;}
if (strstr(chopt,"F")) fitOption.Minuit = 1;
if (strstr(chopt,"C")) fitOption.Nochisq = 1;
return 1;
}
//______________________________________________________________________________
void H1InitGaus()
{
// -*-*-*-*Compute Initial values of parameters for a gaussian*-*-*-*-*-*-*
// ===================================================
Double_t allcha, sumx, sumx2, x, val, rms, mean;
Int_t bin;
const Double_t sqrtpi = 2.506628;
// - Compute mean value and RMS of the histogram in the given range
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
TH1 *curHist = (TH1*)hFitter->GetObjectFit();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
Double_t valmax = curHist->GetBinContent(hxfirst);
Double_t binwidx = curHist->GetBinWidth(hxfirst);
allcha = sumx = sumx2 = 0;
for (bin=hxfirst;bin<=hxlast;bin++) {
x = curHist->GetBinCenter(bin);
val = TMath::Abs(curHist->GetBinContent(bin));
if (val > valmax) valmax = val;
sumx += val*x;
sumx2 += val*x*x;
allcha += val;
}
if (allcha == 0) return;
mean = sumx/allcha;
rms = TMath::Sqrt(sumx2/allcha - mean*mean);
if (rms == 0) rms = binwidx*(hxlast-hxfirst+1)/4;
//if the distribution is really gaussian, the best approximation
//is binwidx*allcha/(sqrtpi*rms)
//However, in case of non-gaussian tails, this underestimates
//the normalisation constant. In this case the maximum value
//is a better approximation.
//We take the average of both quantities
Double_t constant = 0.5*(valmax+binwidx*allcha/(sqrtpi*rms));
//In case the mean value is outside the histo limits and
//the RMS is bigger than the range, we take
// mean = center of bins
// rms = half range
Axis_t xmin = curHist->GetXaxis()->GetXmin();
Axis_t xmax = curHist->GetXaxis()->GetXmax();
if ((mean < xmin || mean > xmax) && rms > (xmax-xmin)) {
mean = 0.5*(xmax+xmin);
rms = 0.5*(xmax-xmin);
}
TF1 *f1 = (TF1*)hFitter->GetUserFunc();
f1->SetParameter(0,constant);
f1->SetParameter(1,mean);
f1->SetParameter(2,rms);
f1->SetParLimits(2,0,10*rms);
}
//______________________________________________________________________________
void H1InitExpo()
{
// -*-*-*-*Compute Initial values of parameters for an exponential*-*-*-*-*
// =======================================================
Double_t constant, slope;
Int_t ifail;
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
Int_t nchanx = hxlast - hxfirst + 1;
H1LeastSquareLinearFit(-nchanx, constant, slope, ifail);
TF1 *f1 = (TF1*)hFitter->GetUserFunc();
f1->SetParameter(0,constant);
f1->SetParameter(1,slope);
}
//______________________________________________________________________________
void H1InitPolynom()
{
// -*-*-*-*Compute Initial values of parameters for a polynom*-*-*-*-*-*-*
// ===================================================
Double_t fitpar[25];
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
TF1 *f1 = (TF1*)hFitter->GetUserFunc();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
Int_t nchanx = hxlast - hxfirst + 1;
Int_t npar = f1->GetNpar();
if (nchanx <=1 || npar == 1) {
TH1 *curHist = (TH1*)hFitter->GetObjectFit();
fitpar[0] = curHist->GetSumOfWeights()/Double_t(nchanx);
} else {
H1LeastSquareFit( nchanx, npar, fitpar);
}
for (Int_t i=0;i<npar;i++) f1->SetParameter(i, fitpar[i]);
}
//______________________________________________________________________________
void H1LeastSquareFit(Int_t n, Int_t m, Double_t *a)
{
// -*-*-*-*-*-*Least squares lpolynomial fitting without weights*-*-*-*-*-*-*
// =================================================
//
// n number of points to fit
// m number of parameters
// a array of parameters
//
// based on CERNLIB routine LSQ: Translated to C++ by Rene Brun
// (E.Keil. revised by B.Schorr, 23.10.1981.)
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
const Double_t zero = 0.;
const Double_t one = 1.;
const Int_t idim = 20;
Double_t b[400] /* was [20][20] */;
Int_t i, k, l, ifail;
Double_t power;
Double_t da[20], xk, yk;
if (m <= 2) {
H1LeastSquareLinearFit(n, a[0], a[1], ifail);
return;
}
if (m > idim || m > n) return;
b[0] = Double_t(n);
da[0] = zero;
for (l = 2; l <= m; ++l) {
b[l-1] = zero;
b[m + l*20 - 21] = zero;
da[l-1] = zero;
}
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
TH1 *curHist = (TH1*)hFitter->GetObjectFit();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
for (k = hxfirst; k <= hxlast; ++k) {
xk = curHist->GetBinCenter(k);
yk = curHist->GetBinContent(k);
power = one;
da[0] += yk;
for (l = 2; l <= m; ++l) {
power *= xk;
b[l-1] += power;
da[l-1] += power*yk;
}
for (l = 2; l <= m; ++l) {
power *= xk;
b[m + l*20 - 21] += power;
}
}
for (i = 3; i <= m; ++i) {
for (k = i; k <= m; ++k) {
b[k - 1 + (i-1)*20 - 21] = b[k + (i-2)*20 - 21];
}
}
H1LeastSquareSeqnd(m, b, idim, ifail, 1, da);
for (i=0; i<m; ++i) a[i] = da[i];
}
//______________________________________________________________________________
void H1LeastSquareLinearFit(Int_t ndata, Double_t &a0, Double_t &a1, Int_t &ifail)
{
// -*-*-*-*-*-*-*-*Least square linear fit without weights*-*-*-*-*-*-*-*-*
// =======================================
//
// extracted from CERNLIB LLSQ: Translated to C++ by Rene Brun
// (added to LSQ by B. Schorr, 15.02.1982.)
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Double_t xbar, ybar, x2bar;
Int_t i, n;
Double_t xybar;
Double_t fn, xk, yk;
Double_t det;
n = TMath::Abs(ndata);
ifail = -2;
xbar = ybar = x2bar = xybar = 0;
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
TH1 *curHist = (TH1*)hFitter->GetObjectFit();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
for (i = hxfirst; i <= hxlast; ++i) {
xk = curHist->GetBinCenter(i);
yk = curHist->GetBinContent(i);
if (ndata < 0) {
if (yk <= 0) yk = 1e-9;
yk = TMath::Log(yk);
}
xbar += xk;
ybar += yk;
x2bar += xk*xk;
xybar += xk*yk;
}
fn = Double_t(n);
det = fn*x2bar - xbar*xbar;
ifail = -1;
if (det <= 0) {
a0 = ybar/fn;
a1 = 0;
return;
}
ifail = 0;
a0 = (x2bar*ybar - xbar*xybar) / det;
a1 = (fn*xybar - xbar*ybar) / det;
}
//______________________________________________________________________________
void H1LeastSquareSeqnd(Int_t n, Double_t *a, Int_t idim, Int_t &ifail, Int_t k, Double_t *b)
{
// -*-*-*-*-*-*Extracted from CERN Program library routine DSEQN*-*-*-*-*-*
// =================================================
//
// : Translated to C++ by Rene Brun
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t a_dim1, a_offset, b_dim1, b_offset;
Int_t nmjp1, i, j, l;
Int_t im1, jp1, nm1, nmi;
Double_t s1, s21, s22;
const Double_t one = 1.;
/* Parameter adjustments */
b_dim1 = idim;
b_offset = b_dim1 + 1;
b -= b_offset;
a_dim1 = idim;
a_offset = a_dim1 + 1;
a -= a_offset;
if (idim < n) return;
ifail = 0;
for (j = 1; j <= n; ++j) {
if (a[j + j*a_dim1] <= 0) { ifail = -1; return; }
a[j + j*a_dim1] = one / a[j + j*a_dim1];
if (j == n) continue;
jp1 = j + 1;
for (l = jp1; l <= n; ++l) {
a[j + l*a_dim1] = a[j + j*a_dim1] * a[l + j*a_dim1];
s1 = -a[l + (j+1)*a_dim1];
for (i = 1; i <= j; ++i) { s1 = a[l + i*a_dim1] * a[i + (j+1)*a_dim1] + s1; }
a[l + (j+1)*a_dim1] = -s1;
}
}
if (k <= 0) return;
for (l = 1; l <= k; ++l) {
b[l*b_dim1 + 1] = a[a_dim1 + 1]*b[l*b_dim1 + 1];
}
if (n == 1) return;
for (l = 1; l <= k; ++l) {
for (i = 2; i <= n; ++i) {
im1 = i - 1;
s21 = -b[i + l*b_dim1];
for (j = 1; j <= im1; ++j) {
s21 = a[i + j*a_dim1]*b[j + l*b_dim1] + s21;
}
b[i + l*b_dim1] = -a[i + i*a_dim1]*s21;
}
nm1 = n - 1;
for (i = 1; i <= nm1; ++i) {
nmi = n - i;
s22 = -b[nmi + l*b_dim1];
for (j = 1; j <= i; ++j) {
nmjp1 = n - j + 1;
s22 = a[nmi + nmjp1*a_dim1]*b[nmjp1 + l*b_dim1] + s22;
}
b[nmi + l*b_dim1] = -s22;
}
}
}
//______________________________________________________________________________
Int_t TH1::GetBin(Int_t binx, Int_t biny, Int_t binz) const
{
// -*-*-*-*Return Global bin number corresponding to binx,y,z*-*-*-*-*-*-*
// ==================================================
//
// 2-D and 3-D histograms are represented with a one dimensional
// structure.
// This has the advantage that all existing functions, such as
// GetBinContent, GetBinError, GetBinFunction work for all dimensions.
//
// In case of a TH1x, returns binx directly.
//
// Convention for numbering bins
// =============================
// For all histogram types: nbins, xlow, xup
// bin = 0; underflow bin
// bin = 1; first bin with low-edge xlow INCLUDED
// bin = nbins; last bin with upper-edge xup EXCLUDED
// bin = nbins+1; overflow bin
// In case of 2-D or 3-D histograms, a "global bin" number is defined.
// For example, assuming a 3-D histogram with binx,biny,binz, the function
// Int_t bin = h->GetBin(binx,biny,binz);
// returns a global/linearized bin number. This global bin is useful
// to access the bin information independently of the dimension.
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t nx, ny, nz;
if (GetDimension() < 2) {
nx = fXaxis.GetNbins()+2;
if (binx < 0) binx = 0;
if (binx >= nx) binx = nx-1;
return binx;
}
if (GetDimension() < 3) {
nx = fXaxis.GetNbins()+2;
if (binx < 0) binx = 0;
if (binx >= nx) binx = nx-1;
ny = fYaxis.GetNbins()+2;
if (biny < 0) biny = 0;
if (biny >= ny) biny = ny-1;
return binx + nx*biny;
}
if (GetDimension() < 4) {
nx = fXaxis.GetNbins()+2;
if (binx < 0) binx = 0;
if (binx >= nx) binx = nx-1;
ny = fYaxis.GetNbins()+2;
if (biny < 0) biny = 0;
if (biny >= ny) biny = ny-1;
nz = fZaxis.GetNbins()+2;
if (binz < 0) binz = 0;
if (binz >= nz) binz = nz-1;
return binx + nx*(biny +ny*binz);
}
return -1;
}
//______________________________________________________________________________
Axis_t TH1::GetRandom() const
{
// return a random number distributed according the histogram bin contents.
// This function checks if the bins integral exists. If not, the integral
// is evaluated, normalized to one.
// The integral is automatically recomputed if the number of entries
// is not the same then when the integral was computed.
// NB Only valid for 1-d histograms. Use GetRandom2 or 3 otherwise.
if (fDimension > 1) {
Error("GetRandom","Function only valid for 1-d histograms");
return 0;
}
Int_t nbinsx = GetNbinsX();
Double_t integral;
if (fIntegral) {
if (fIntegral[nbinsx+1] != fEntries) integral = ((TH1*)this)->ComputeIntegral();
} else {
integral = ((TH1*)this)->ComputeIntegral();
if (integral == 0 || fIntegral == 0) return 0;
}
Double_t r1 = gRandom->Rndm();
Int_t ibin = TMath::BinarySearch(nbinsx,fIntegral,r1);
return GetBinLowEdge(ibin+1)
+GetBinWidth(ibin+1)*(r1-fIntegral[ibin])/(fIntegral[ibin+1] - fIntegral[ibin]);
}
//______________________________________________________________________________
Stat_t TH1::GetBinContent(Int_t) const
{
// -*-*-*-*-*Return content of bin number bin
// ================================
// Implemented in TH1C,S,F,D
//
// Convention for numbering bins
// =============================
// For all histogram types: nbins, xlow, xup
// bin = 0; underflow bin
// bin = 1; first bin with low-edge xlow INCLUDED
// bin = nbins; last bin with upper-edge xup EXCLUDED
// bin = nbins+1; overflow bin
// In case of 2-D or 3-D histograms, a "global bin" number is defined.
// For example, assuming a 3-D histogram with binx,biny,binz, the function
// Int_t bin = h->GetBin(binx,biny,binz);
// returns a global/linearized bin number. This global bin is useful
// to access the bin information independently of the dimension.
AbstractMethod("GetBinContent");
return 0;
}
//______________________________________________________________________________
Stat_t TH1::GetBinContent(Int_t binx, Int_t biny) const
{
// -*-*-*-*-*Return content of bin number binx, biny
// =======================================
// NB: Function to be called for 2-d histograms only
// see convention for numbering bins in TH1::GetBin
Int_t bin = GetBin(binx,biny);
return GetBinContent(bin);
}
//______________________________________________________________________________
Stat_t TH1::GetBinContent(Int_t binx, Int_t biny, Int_t binz) const
{
// -*-*-*-*-*Return content of bin number binx,biny,binz
// ===========================================
// NB: Function to be called for 3-d histograms only
// see convention for numbering bins in TH1::GetBin
Int_t bin = GetBin(binx,biny,binz);
return GetBinContent(bin);
}
//______________________________________________________________________________
TAxis *TH1::GetXaxis() const
{
// return a pointer to the X axis object
return &((TH1*)this)->fXaxis;
}
//______________________________________________________________________________
TAxis *TH1::GetYaxis() const
{
// return a pointer to the Y axis object
return &((TH1*)this)->fYaxis;
}
//______________________________________________________________________________
TAxis *TH1::GetZaxis() const
{
// return a pointer to the Z axis object
return &((TH1*)this)->fZaxis;
}
//___________________________________________________________________________
void TH1::LabelsDeflate(Option_t *ax)
{
// Reduce the number of bins for this axis to the number of bins having a label.
Int_t iaxis = AxisChoice(ax);
TAxis *axis = 0;
if (iaxis == 1) axis = GetXaxis();
if (iaxis == 2) axis = GetYaxis();
if (iaxis == 3) axis = GetZaxis();
if (!axis) return;
if (!axis->GetLabels()) return;
TIter next(axis->GetLabels());
TObject *obj;
Int_t nbins = 0;
while ((obj = next())) {
if (obj->GetUniqueID()) nbins++;
}
if (nbins < 1) nbins = 1;
TH1 *hold = (TH1*)Clone();
hold->SetDirectory(0);
Bool_t timedisp = axis->GetTimeDisplay();
Double_t xmin = axis->GetXmin();
Double_t xmax = axis->GetBinUpEdge(nbins);
if (xmax <= xmin) xmax = xmin +nbins;
axis->SetRange(0,0);
axis->Set(nbins,xmin,xmax);
//Int_t nbinsx = fXaxis.GetNbins();
//Int_t nbinsy = fYaxis.GetNbins();
//Int_t nbinsz = fZaxis.GetNbins();
Int_t nbinsx = hold->GetXaxis()->GetNbins();
Int_t nbinsy = hold->GetYaxis()->GetNbins();
Int_t nbinsz = hold->GetZaxis()->GetNbins();
Int_t ncells = nbinsx+2;
if (GetDimension() > 1) ncells *= nbinsy+2;
if (GetDimension() > 2) ncells *= nbinsz+2;
SetBinsLength(ncells);
Int_t errors = fSumw2.fN;
if (errors) fSumw2.Set(ncells);
axis->SetTimeDisplay(timedisp);
//now loop on all bins and refill
Double_t err,cu;
Int_t bin,ibin,binx,biny,binz;
Double_t oldEntries = fEntries;
for (binz=1;binz<=nbinsz;binz++) {
for (biny=1;biny<=nbinsy;biny++) {
for (binx=1;binx<=nbinsx;binx++) {
bin = hold->GetBin(binx,biny,binz);
ibin= GetBin(binx,biny,binz);
cu = hold->GetBinContent(bin);
SetBinContent(ibin,cu);
if (errors) {
err = hold->GetBinError(bin);
SetBinError(ibin,err);
}
}
}
}
fEntries = oldEntries;
delete hold;
}
//______________________________________________________________________________
void TH1::LabelsInflate(Option_t *ax)
{
// Double the number of bins for axis.
// Refill histogram
// This function is called by TAxis::FindBin(const char *label)
Int_t iaxis = AxisChoice(ax);
TAxis *axis = 0;
if (iaxis == 1) axis = GetXaxis();
if (iaxis == 2) axis = GetYaxis();
if (iaxis == 3) axis = GetZaxis();
if (!axis) return;
TH1 *hold = (TH1*)Clone();
hold->SetDirectory(0);
Bool_t timedisp = axis->GetTimeDisplay();
Int_t nbxold = fXaxis.GetNbins();
Int_t nbyold = fYaxis.GetNbins();
Int_t nbzold = fZaxis.GetNbins();
Int_t nbins = axis->GetNbins();
Double_t xmin = axis->GetXmin();
Double_t xmax = axis->GetXmax();
xmax = xmin + 2*(xmax-xmin);
axis->SetRange(0,0);
axis->Set(2*nbins,xmin,xmax);
Int_t nbinsx = fXaxis.GetNbins();
Int_t nbinsy = fYaxis.GetNbins();
Int_t nbinsz = fZaxis.GetNbins();
Int_t ncells = nbinsx+2;
if (GetDimension() > 1) ncells *= nbinsy+2;
if (GetDimension() > 2) ncells *= nbinsz+2;
SetBinsLength(ncells);
Int_t errors = fSumw2.fN;
if (errors) fSumw2.Set(ncells);
axis->SetTimeDisplay(timedisp);
//now loop on all bins and refill
Double_t err,cu;
Int_t bin,ibin,binx,biny,binz;
for (binz=1;binz<=nbinsz;binz++) {
for (biny=1;biny<=nbinsy;biny++) {
for (binx=1;binx<=nbinsx;binx++) {
bin = hold->GetBin(binx,biny,binz);
ibin= GetBin(binx,biny,binz);
if (binx > nbxold || biny > nbyold || binz > nbzold) bin = -1;
if (bin > 0) cu = hold->GetBinContent(bin);
else cu = 0;
SetBinContent(ibin,cu);
if (errors) {
if (bin > 0) err = hold->GetBinError(bin);
else err = 0;
SetBinError(ibin,err);
}
}
}
}
delete hold;
}
//______________________________________________________________________________
void TH1::LabelsOption(Option_t *option, Option_t *ax)
{
// Set option(s) to draw axis with labels
// option = "a" sort by alphabetic order
// = ">" sort by decreasing values
// = "<" sort by increasing values
// = "h" draw labels horizonthal
// = "v" draw labels vertical
// = "u" draw labels up (end of label right adjusted)
// = "d" draw labels down (start of label left adjusted)
Int_t iaxis = AxisChoice(ax);
TAxis *axis = 0;
if (iaxis == 1) axis = GetXaxis();
if (iaxis == 2) axis = GetYaxis();
if (iaxis == 3) axis = GetZaxis();
if (!axis) return;
THashList *labels = axis->GetLabels();
if (!labels) {
Warning("LabelsOption","Cannot sort. No labels");
return;
}
TString opt = option;
opt.ToLower();
if (opt.Contains("h")) {
axis->SetBit(TAxis::kLabelsHori);
axis->ResetBit(TAxis::kLabelsVert);
axis->ResetBit(TAxis::kLabelsDown);
axis->ResetBit(TAxis::kLabelsUp);
}
if (opt.Contains("v")) {
axis->SetBit(TAxis::kLabelsVert);
axis->ResetBit(TAxis::kLabelsHori);
axis->ResetBit(TAxis::kLabelsDown);
axis->ResetBit(TAxis::kLabelsUp);
}
if (opt.Contains("u")) {
axis->SetBit(TAxis::kLabelsUp);
axis->ResetBit(TAxis::kLabelsVert);
axis->ResetBit(TAxis::kLabelsDown);
axis->ResetBit(TAxis::kLabelsHori);
}
if (opt.Contains("d")) {
axis->SetBit(TAxis::kLabelsDown);
axis->ResetBit(TAxis::kLabelsVert);
axis->ResetBit(TAxis::kLabelsHori);
axis->ResetBit(TAxis::kLabelsUp);
}
Int_t sort = -1;
if (opt.Contains("a")) sort = 0;
if (opt.Contains(">")) sort = 1;
if (opt.Contains("<")) sort = 2;
if (sort < 0) return;
if (sort > 0 && GetDimension() > 2) {
Error("LabelsOption","Sorting by value not implemented for 3-D histograms");
return;
}
Int_t n = TMath::Min(axis->GetNbins(), labels->GetSize());
Int_t *a = new Int_t[n+2];
Int_t i,j,k;
Double_t *cont = 0;
Double_t *errors = 0;
THashList *labold = new THashList(labels->GetSize(),1);
TIter nextold(labels);
TObject *obj;
while ((obj=nextold())) {
labold->Add(obj);
}
labels->Clear();
if (sort > 0) {
//---sort by values of bins
if (GetDimension() == 1) {
cont = new Double_t[n];
if (fSumw2.fN) errors = new Double_t[n];
for (i=1;i<=n;i++) {
cont[i-1] = GetBinContent(i);
if (errors) errors[i-1] = GetBinError(i);
}
if (sort ==1) TMath::Sort(n,cont,a,kTRUE); //sort by decreasing values
else TMath::Sort(n,cont,a,kFALSE); //sort by increasing values
for (i=1;i<=n;i++) {
SetBinContent(i,cont[a[i-1]]);
if (errors) SetBinError(i,errors[a[i-1]]);
}
for (i=1;i<=n;i++) {
obj = labold->At(a[i-1]);
labels->Add(obj);
obj->SetUniqueID(i);
}
} else if (GetDimension()== 2) {
Double_t *pcont = new Double_t[n+2];
for (i=0;i<=n;i++) pcont[i] = 0;
Int_t nx = fXaxis.GetNbins();
Int_t ny = fYaxis.GetNbins();
cont = new Double_t[(nx+2)*(ny+2)];
if (fSumw2.fN) errors = new Double_t[n];
for (i=1;i<=nx;i++) {
for (j=1;j<=ny;j++) {
cont[i+nx*j] = GetBinContent(i,j);
if (errors) errors[i+nx*j] = GetBinError(i,j);
if (axis == GetXaxis()) k = i;
else k = j;
pcont[k-1] += cont[i+nx*j];
}
}
if (sort ==1) TMath::Sort(n,pcont,a,kTRUE); //sort by decreasing values
else TMath::Sort(n,pcont,a,kFALSE); //sort by increasing values
for (i=0;i<n;i++) {
obj = labold->At(a[i]);
labels->Add(obj);
obj->SetUniqueID(i+1);
}
delete [] pcont;
for (i=1;i<=nx;i++) {
for (j=1;j<=ny;j++) {
if (axis == GetXaxis()) {
SetBinContent(i,j,cont[a[i-1]+1+nx*j]);
if (errors) SetBinError(i,j,errors[a[i-1]+1+nx*j]);
} else {
SetBinContent(i,j,cont[i+nx*(a[j-1]+1)]);
if (errors) SetBinError(i,j,errors[i+nx*(a[j-1]+1)]);
}
}
}
} else {
//to be implemented
}
} else {
//---alphabetic sort
const UInt_t kUsed = 1<<18;
TObject *objk=0;
a[0] = 0;
a[n+1] = n+1;
for (i=1;i<=n;i++) {
const char *label = "zzzzzzzzzzzz";
for (j=1;j<=n;j++) {
obj = labold->At(j-1);
if (!obj) continue;
if (obj->TestBit(kUsed)) continue;
//use strcasecmp for case non-sensitive sort (may be an option)
if (strcmp(label,obj->GetName()) < 0) continue;
objk = obj;
a[i] = j;
label = obj->GetName();
}
if (objk) {
objk->SetUniqueID(i);
labels->Add(objk);
objk->SetBit(kUsed);
}
}
for (i=1;i<=n;i++) {
obj = labels->At(i-1);
if (!obj) continue;
obj->ResetBit(kUsed);
}
if (GetDimension() == 1) {
cont = new Double_t[n+2];
if (fSumw2.fN) errors = new Double_t[n+2];
for (i=1;i<=n;i++) {
cont[i] = GetBinContent(a[i]);
if (errors) errors[i] = GetBinError(a[i]);
}
for (i=1;i<=n;i++) {
SetBinContent(i,cont[i]);
if (errors) SetBinError(i,errors[i]);
}
} else if (GetDimension()== 2) {
Int_t nx = fXaxis.GetNbins()+2;
Int_t ny = fYaxis.GetNbins()+2;
cont = new Double_t[nx*ny];
if (fSumw2.fN) errors = new Double_t[nx*ny];
for (i=0;i<nx;i++) {
for (j=0;j<ny;j++) {
cont[i+nx*j] = GetBinContent(i,j);
if (errors) errors[i+nx*j] = GetBinError(i,j);
}
}
for (i=0;i<nx;i++) {
for (j=0;j<ny;j++) {
if (axis == GetXaxis()) {
SetBinContent(i,j,cont[a[i]+nx*j]);
if (errors) SetBinError(i,j,errors[a[i]+nx*j]);
} else {
SetBinContent(i,j,cont[i+nx*a[j]]);
if (errors) SetBinError(i,j,errors[i+nx*a[j]]);
}
}
}
} else {
Int_t nx = fXaxis.GetNbins()+2;
Int_t ny = fYaxis.GetNbins()+2;
Int_t nz = fZaxis.GetNbins()+2;
cont = new Double_t[nx*ny*nz];
if (fSumw2.fN) errors = new Double_t[nx*ny*nz];
for (i=0;i<nx;i++) {
for (j=0;j<ny;j++) {
for (k=0;k<nz;k++) {
cont[i+nx*(j+ny*k)] = GetBinContent(i,j,k);
if (errors) errors[i+nx*(j+ny*k)] = GetBinError(i,j,k);
}
}
}
for (i=0;i<nx;i++) {
for (j=0;j<ny;j++) {
for (k=0;k<nz;k++) {
if (axis == GetXaxis()) {
SetBinContent(i,j,k,cont[a[i]+nx*(j+ny*k)]);
if (errors) SetBinError(i,j,k,errors[a[i]+nx*(j+ny*k)]);
} else if (axis == GetYaxis()) {
SetBinContent(i,j,k,cont[i+nx*(a[j]+ny*k)]);
if (errors) SetBinError(i,j,k,errors[i+nx*(a[j]+ny*k)]);
} else {
SetBinContent(i,j,k,cont[i+nx*(j+ny*a[k])]);
if (errors) SetBinError(i,j,k,errors[i+nx*(j+ny*a[k])]);
}
}
}
}
}
}
delete labold;
if (a) delete [] a;
if (cont) delete [] cont;
if (errors) delete [] errors;
}
//______________________________________________________________________________
static Bool_t AlmostEqual(Double_t a, Double_t b, Double_t epsilon = 0.00000001)
{
return TMath::Abs(a - b) < epsilon;
}
//______________________________________________________________________________
static Bool_t AlmostInteger(Double_t a, Double_t epsilon = 0.00000001)
{
return AlmostEqual(a - TMath::Floor(a), 0, epsilon) ||
AlmostEqual(a - TMath::Floor(a), 1, epsilon);
}
//______________________________________________________________________________
Bool_t TH1::SameLimitsAndNBins(const TAxis& axis1, const TAxis& axis2)
{
if ((axis1.GetNbins() == axis2.GetNbins())
&& (axis1.GetXmin() == axis2.GetXmin())
&& (axis1.GetXmax() == axis2.GetXmax()))
return kTRUE;
else
return kFALSE;
}
//______________________________________________________________________________
Bool_t TH1::RecomputeAxisLimits(TAxis& destAxis, const TAxis& anAxis)
{
// Finds new limits for the axis for the Merge function.
// returns false if the limits are incompatible
if (SameLimitsAndNBins(destAxis, anAxis))
return kTRUE;
if (destAxis.GetXbins()->fN || anAxis.GetXbins()->fN)
return kFALSE; // user binning not supported
Axis_t width1 = destAxis.GetBinWidth(0);
Axis_t width2 = anAxis.GetBinWidth(0);
if (width1 == 0 || width2 == 0)
return kFALSE; // no binning not supported
Axis_t xmin = TMath::Min(destAxis.GetXmin(), anAxis.GetXmin());
Axis_t xmax = TMath::Max(destAxis.GetXmax(), anAxis.GetXmax());
Axis_t width = TMath::Max(width1, width2);
// check the bin size
if (!AlmostInteger(width/width1) || !AlmostInteger(width/width2))
return kFALSE;
// check the limits
Axis_t delta;
delta = (destAxis.GetXmin() - xmin)/width1;
if (!AlmostInteger(delta))
xmin -= (TMath::Ceil(delta) - delta)*width1;
delta = (anAxis.GetXmin() - xmin)/width2;
if (!AlmostInteger(delta))
xmin -= (TMath::Ceil(delta) - delta)*width2;
delta = (destAxis.GetXmin() - xmin)/width1;
if (!AlmostInteger(delta))
return kFALSE;
delta = (xmax - destAxis.GetXmax())/width1;
if (!AlmostInteger(delta))
xmax += (TMath::Ceil(delta) - delta)*width1;
delta = (xmax - anAxis.GetXmax())/width2;
if (!AlmostInteger(delta))
xmax += (TMath::Ceil(delta) - delta)*width2;
delta = (xmax - destAxis.GetXmax())/width1;
if (!AlmostInteger(delta))
return kFALSE;
#ifdef DEBUG
if (!AlmostInteger((xmax - xmin) / width)) { // unnecessary check
printf("TH1::RecomputeAxisLimits - Impossible\n");
return kFALSE;
}
#endif
destAxis.Set(TMath::Nint((xmax - xmin)/width), xmin, xmax);
return kTRUE;
}
//______________________________________________________________________________
Long64_t TH1::Merge(TCollection *li)
{
// Add all histograms in the collection to this histogram.
// This function computes the min/max for the x axis,
// compute a new number of bins, if necessary,
// add bin contents, errors and statistics.
// If all histograms have bin labels, bins with identical labels
// will be merged, no matter what their order is.
// If overflows are present and limits are different the function will fail.
// The function returns the total number of entries in the result histogram
// if the merge is successfull, -1 otherwise.
//
// IMPORTANT remark. The axis x may have different number
// of bins and different limits, BUT the largest bin width must be
// a multiple of the smallest bin width and the upper limit must also
// be a multiple of the bin width.
// Example:
// void atest() {
// TH1F *h1 = new TH1F("h1","h1",110,-110,0);
// TH1F *h2 = new TH1F("h2","h2",220,0,110);
// TH1F *h3 = new TH1F("h3","h3",330,-55,55);
// TRandom r;
// for (Int_t i=0;i<10000;i++) {
// h1->Fill(r.Gaus(-55,10));
// h2->Fill(r.Gaus(55,10));
// h3->Fill(r.Gaus(0,10));
// }
//
// TList *list = new TList;
// list->Add(h1);
// list->Add(h2);
// list->Add(h3);
// TH1F *h = (TH1F*)h1->Clone("h");
// h->Reset();
// h.Merge(list);
// h->Draw();
// }
if (!li) return 0;
if (li->IsEmpty()) return (Int_t) GetEntries();
TList inlist;
TH1* hclone = (TH1*)Clone("FirstClone");
BufferEmpty(1); // To remove buffer.
Reset(); // BufferEmpty sets limits so we can't use it later.
SetEntries(0);
inlist.Add(hclone);
inlist.AddAll(li);
THashList allLabels;
THashList* labels=GetXaxis()->GetLabels();
Bool_t haveOneLabel=kFALSE;
if (labels) {
TIter iL(labels);
TObjString* lb;
while ((lb=(TObjString*)iL())) {
haveOneLabel |= (lb && lb->String().Length());
if (!allLabels.FindObject(lb))
allLabels.Add(lb);
}
}
TAxis newXAxis;
Bool_t initialLimitsFound = kFALSE;
Bool_t allHaveLabels = haveOneLabel;
Bool_t same = kTRUE;
Bool_t allHaveLimits = kTRUE;
TIter next(&inlist);
while (TObject *o = next()) {
TH1* h = dynamic_cast<TH1*> (o);
if (!h) {
Error("Add","Attempt to add object of class: %s to a %s",
o->ClassName(),this->ClassName());
return -1;
}
Bool_t hasLimits = h->GetXaxis()->GetXmin() < h->GetXaxis()->GetXmax();
allHaveLimits = allHaveLimits && hasLimits;
if (hasLimits) {
h->BufferEmpty();
if (!initialLimitsFound) {
initialLimitsFound = kTRUE;
newXAxis.Set(h->GetXaxis()->GetNbins(), h->GetXaxis()->GetXmin(),
h->GetXaxis()->GetXmax());
}
else {
if (!RecomputeAxisLimits(newXAxis, *(h->GetXaxis()))) {
Error("Merge", "Cannot merge histograms - limits are inconsistent:\n "
"first: (%d, %f, %f), second: (%d, %f, %f)",
newXAxis.GetNbins(), newXAxis.GetXmin(), newXAxis.GetXmax(),
h->GetXaxis()->GetNbins(), h->GetXaxis()->GetXmin(),
h->GetXaxis()->GetXmax());
}
}
}
if (allHaveLabels) {
THashList* labels=h->GetXaxis()->GetLabels();
Bool_t haveOneLabel=kFALSE;
if (labels) {
TIter iL(labels);
TObjString* lb;
while ((lb=(TObjString*)iL())) {
haveOneLabel |= (lb && lb->String().Length());
if (!allLabels.FindObject(lb)) {
allLabels.Add(lb);
same = kFALSE;
}
}
}
allHaveLabels&=(labels && haveOneLabel);
if (!allHaveLabels)
Warning("Merge","Not all histograms have labels. I will ignore labels,"
" falling back to bin numbering mode.");
}
}
next.Reset();
same = same && SameLimitsAndNBins(newXAxis, *GetXaxis());
if (!same && initialLimitsFound)
SetBins(newXAxis.GetNbins(), newXAxis.GetXmin(), newXAxis.GetXmax());
if (!allHaveLimits) {
// fill this histogram with all the data from buffers of histograms without limits
while (TH1* h = (TH1*)next()) {
if (h->GetXaxis()->GetXmin() >= h->GetXaxis()->GetXmax() && h->fBuffer) {
// no limits
Int_t nbentries = (Int_t)h->fBuffer[0];
for (Int_t i = 0; i < nbentries; i++)
Fill(h->fBuffer[2*i + 2], h->fBuffer[2*i + 1]);
// Entries from buffers have to be filled one by one
// because FillN doesn't resize histograms.
}
}
if (!initialLimitsFound)
return (Int_t) GetEntries(); // all histograms have been processed
next.Reset();
}
//merge bin contents and errors
Stat_t stats[kNstat], totstats[kNstat];
for (Int_t i=0;i<kNstat;i++) {totstats[i] = stats[i] = 0;}
GetStats(totstats);
Stat_t nentries = GetEntries();
Int_t binx, ix, nx;
Double_t cu;
Bool_t canRebin=TestBit(kCanRebin);
ResetBit(kCanRebin); // reset, otherwise setting the under/overflow will rebin
while (TH1* h=(TH1*)next()) {
// process only if the histogram has limits; otherwise it was processed before
if (h->GetXaxis()->GetXmin() < h->GetXaxis()->GetXmax()) {
// import statistics
h->GetStats(stats);
for (Int_t i=0;i<kNstat;i++)
totstats[i] += stats[i];
nentries += h->GetEntries();
nx = h->GetXaxis()->GetNbins();
for (binx = 0; binx <= nx + 1; binx++) {
cu = h->GetBinContent(binx);
if (!allHaveLabels || !binx || binx==nx+1) {
if ((!same) && (binx == 0 || binx == nx + 1)) {
if (cu != 0) {
Error("Merge", "Cannot merge histograms - the histograms have"
" different limits and undeflows/overflows are present."
" The initial histogram is now broken!");
return -1;
}
}
ix = fXaxis.FindBin(h->GetXaxis()->GetBinCenter(binx));
} else {
const char* label=h->GetXaxis()->GetBinLabel(binx);
if (!label) label="";
ix = fXaxis.FindBin(label);
}
AddBinContent(ix,cu);
if (fSumw2.fN) {
Double_t error1 = h->GetBinError(binx);
fSumw2.fArray[ix] += error1*error1;
}
}
}
}
if (canRebin) SetBit(kCanRebin);
//copy merged stats
PutStats(totstats);
SetEntries(nentries);
if (hclone) delete hclone;
return (Long64_t)nentries;
}
//______________________________________________________________________________
void TH1::Multiply(TF1 *f1, Double_t c1)
{
// Performs the operation: this = this*c1*f1
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
//
// Only bins inside the function range are recomputed.
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Multiply
if (!f1) {
Error("Add","Attempt to multiply by a non-existing function");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// - Add statistics
Double_t nEntries = fEntries;
Stat_t s1[10];
Int_t i;
for (i=0;i<10;i++) {s1[i] = 0;}
PutStats(s1);
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu,w;
Double_t xx[3];
Double_t *params = 0;
f1->InitArgs(xx,params);
for (binz=0;binz<=nbinsz+1;binz++) {
xx[2] = fZaxis.GetBinCenter(binz);
for (biny=0;biny<=nbinsy+1;biny++) {
xx[1] = fYaxis.GetBinCenter(biny);
for (binx=0;binx<=nbinsx+1;binx++) {
xx[0] = fXaxis.GetBinCenter(binx);
if (!f1->IsInside(xx)) continue;
TF1::RejectPoint(kFALSE);
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
Double_t error1 = GetBinError(bin);
cu = c1*f1->EvalPar(xx);
if (TF1::RejectedPoint()) continue;
w = GetBinContent(bin)*cu;
SetBinContent(bin,w);
if (fSumw2.fN) {
fSumw2.fArray[bin] = cu*cu*error1*error1;
}
}
}
}
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Multiply(const TH1 *h1)
{
// -*-*-*-*-*-*-*-*-*Multiply this histogram by h1*-*-*-*-*-*-*-*-*-*-*-*-*
// =============================
//
// this = this*h1
//
// If errors of this are available (TH1::Sumw2), errors are recalculated.
// Note that if h1 has Sumw2 set, Sumw2 is automatically called for this
// if not already set.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Multiply
if (!h1) {
Error("Multiply","Attempt to multiply by a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()) {
Error("Multiply","Attempt to multiply histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Multiply","Attempt to multiply histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 has Sumw2 set
if (fSumw2.fN == 0 && h1->GetSumw2N() != 0) Sumw2();
// - Reset statistics
Double_t nEntries = fEntries;
fEntries = fTsumw = 0;
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t c0,c1,w;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = GetBin(binx,biny,binz);
c0 = GetBinContent(bin);
c1 = h1->GetBinContent(bin);
w = c0*c1;
SetBinContent(bin,w);
fEntries++;
if (fSumw2.fN) {
Double_t e0 = GetBinError(bin);
Double_t e1 = h1->GetBinError(bin);
fSumw2.fArray[bin] = (e0*e0*c1*c1 + e1*e1*c0*c0);
}
}
}
}
Stat_t s[kNstat];
GetStats(s);
PutStats(s);
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Multiply(const TH1 *h1, const TH1 *h2, Double_t c1, Double_t c2, Option_t *option)
{
// -*-*-*Replace contents of this histogram by multiplication of h1 by h2*-*
// ================================================================
//
// this = (c1*h1)*(c2*h2)
//
// If errors of this are available (TH1::Sumw2), errors are recalculated.
// Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this
// if not already set.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Multiply
TString opt = option;
opt.ToLower();
// Bool_t binomial = kFALSE;
// if (opt.Contains("b")) binomial = kTRUE;
if (!h1 || !h2) {
Error("Multiply","Attempt to multiply by a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()
|| nbinsx != h2->GetNbinsX() || nbinsy != h2->GetNbinsY() || nbinsz != h2->GetNbinsZ()) {
Error("Multiply","Attempt to multiply histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Multiply","Attempt to multiply histograms with different axis limits");
}
if (fXaxis.GetXmin() != h2->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h2->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h2->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h2->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h2->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h2->fZaxis.GetXmax()) {
Warning("Multiply","Attempt to multiply histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 or h2 have Sumw2 set
if (fSumw2.fN == 0 && (h1->GetSumw2N() != 0 || h2->GetSumw2N() != 0)) Sumw2();
// - Reset statistics
Double_t nEntries = fEntries;
fEntries = fTsumw = fTsumw2 = fTsumwx = fTsumwx2 = 0;
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t b1,b2,w,d1,d2;
d1 = c1*c1;
d2 = c2*c2;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
b1 = h1->GetBinContent(bin);
b2 = h2->GetBinContent(bin);
w = (c1*b1)*(c2*b2);
SetBinContent(bin,w);
fEntries++;
if (fSumw2.fN) {
Double_t e1 = h1->GetBinError(bin);
Double_t e2 = h2->GetBinError(bin);
fSumw2.fArray[bin] = d1*d2*(e1*e1*b2*b2 + e2*e2*b1*b1);
}
}
}
}
Stat_t s[kNstat];
GetStats(s);
PutStats(s);
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Paint(Option_t *option)
{
// -*-*-*-*-*-*-*Control routine to paint any kind of histograms*-*-*-*-*-*-*
// ===============================================
//
// This function is automatically called by TCanvas::Update.
// (see TH1::Draw for the list of options)
GetPainter();
if (fPainter) {
if (strlen(option) > 0) fPainter->Paint(option);
else fPainter->Paint(fOption.Data());
}
}
//______________________________________________________________________________
TH1 *TH1::Rebin(Int_t ngroup, const char*newname)
{
// -*-*-*Rebin this histogram grouping ngroup bins together*-*-*-*-*-*-*-*-*
// ==================================================
// if newname is not blank a new temporary histogram hnew is created.
// else the current histogram is modified (default)
// The parameter ngroup indicates how many bins of this have to me merged
// into one bin of hnew
// If the original histogram has errors stored (via Sumw2), the resulting
// histograms has new errors correctly calculated.
//
// examples: if h1 is an existing TH1F histogram with 100 bins
// h1->Rebin(); //merges two bins in one in h1: previous contents of h1 are lost
// h1->Rebin(5); //merges five bins in one in h1
// TH1F *hnew = h1->Rebin(5,"hnew"); // creates a new histogram hnew
// //merging 5 bins of h1 in one bin
//
// NOTE: If ngroup is not an exact divider of the number of bins,
// the top limit of the rebinned histogram is changed
// to the upper edge of the bin=newbins*ngroup and the corresponding
// bins are added to the overflow bin.
// Statistics will be recomputed from the new bin contents.
Int_t nbins = fXaxis.GetNbins();
Axis_t xmin = fXaxis.GetXmin();
Axis_t xmax = fXaxis.GetXmax();
if ((ngroup <= 0) || (ngroup > nbins)) {
Error("Rebin", "Illegal value of ngroup=%d",ngroup);
return 0;
}
if (fDimension > 1 || InheritsFrom("TProfile")) {
Error("Rebin", "Operation valid on 1-D histograms only");
return 0;
}
Int_t newbins = nbins/ngroup;
// Save old bin contents into a new array
Double_t entries = fEntries;
Double_t *oldBins = new Double_t[nbins];
Int_t bin, i;
for (bin=0;bin<nbins;bin++) oldBins[bin] = GetBinContent(bin+1);
Double_t *oldErrors = 0;
if (fSumw2.fN != 0) {
oldErrors = new Double_t[nbins];
for (bin=0;bin<nbins;bin++) oldErrors[bin] = GetBinError(bin+1);
}
// create a clone of the old histogram if newname is specified
TH1 *hnew = this;
if (newname && strlen(newname) > 0) {
hnew = (TH1*)Clone();
hnew->SetName(newname);
}
// change axis specs and rebuild bin contents array::RebinAx
if(newbins*ngroup != nbins) {
xmax = fXaxis.GetBinUpEdge(newbins*ngroup);
hnew->fTsumw = 0; //stats must be reset because top bins will be moved to overflow bin
}
// save the TAttAxis members (reset by SetBins)
Int_t nDivisions = fXaxis.GetNdivisions();
Color_t axisColor = fXaxis.GetAxisColor();
Color_t labelColor = fXaxis.GetLabelColor();
Style_t labelFont = fXaxis.GetLabelFont();
Float_t labelOffset = fXaxis.GetLabelOffset();
Float_t labelSize = fXaxis.GetLabelSize();
Float_t tickLength = fXaxis.GetTickLength();
Float_t titleOffset = fXaxis.GetTitleOffset();
Float_t titleSize = fXaxis.GetTitleSize();
Color_t titleColor = fXaxis.GetTitleColor();
Style_t titleFont = fXaxis.GetTitleFont();
if(fXaxis.GetXbins()->GetSize() > 0){ // variable bin sizes
Axis_t *bins = new Axis_t[newbins+1];
for(Int_t i = 0; i <= newbins; ++i) bins[i] = fXaxis.GetBinLowEdge(1+i*ngroup);
hnew->SetBins(newbins,bins); //this also changes errors array (if any)
delete [] bins;
} else {
hnew->SetBins(newbins,xmin,xmax); //this also changes errors array (if any)
}
// Restore axis attributes
fXaxis.SetNdivisions(nDivisions);
fXaxis.SetAxisColor(axisColor);
fXaxis.SetLabelColor(labelColor);
fXaxis.SetLabelFont(labelFont);
fXaxis.SetLabelOffset(labelOffset);
fXaxis.SetLabelSize(labelSize);
fXaxis.SetTickLength(tickLength);
fXaxis.SetTitleOffset(titleOffset);
fXaxis.SetTitleSize(titleSize);
fXaxis.SetTitleColor(titleColor);
fXaxis.SetTitleFont(titleFont);
// copy merged bin contents (ignore under/overflows)
Int_t oldbin = 0;
Double_t binContent, binError;
for (bin = 0;bin<=newbins;bin++) {
binContent = 0;
binError = 0;
for (i=0;i<ngroup;i++) {
if (oldbin+i >= nbins) break;
binContent += oldBins[oldbin+i];
if (oldErrors) binError += oldErrors[oldbin+i]*oldErrors[oldbin+i];
}
hnew->SetBinContent(bin+1,binContent);
if (oldErrors) hnew->SetBinError(bin+1,TMath::Sqrt(binError));
oldbin += ngroup;
}
hnew->SetEntries(entries); //was modified by SetBinContent
delete [] oldBins;
if (oldErrors) delete [] oldErrors;
return hnew;
}
//______________________________________________________________________________
Bool_t TH1::FindNewAxisLimits(const TAxis* axis, const Axis_t point, Axis_t& newMin, Axis_t &newMax)
{
// finds new limits for the axis so that *point* is within the range and
// the limits are compatible with the previous ones (see TH1::Merge).
// new limits are put into *newMin* and *newMax* variables.
// axis - axis whose limits are to be recomputed
// point - point that should fit within the new axis limits
// newMin - new minimum will be stored here
// newMax - new maximum will be stored here.
// false if failed (e.g. if the initial axis limits are wrong
// or the new range is more than 2^64 times the old one).
Axis_t xmin = axis->GetXmin();
Axis_t xmax = axis->GetXmax();
if (xmin >= xmax) return kFALSE;
Axis_t range = xmax-xmin;
Axis_t binsize = range / axis->GetNbins();
//recompute new axis limits by doubling the current range
Int_t ntimes = 0;
while (point < xmin) {
if (ntimes++ > 64)
return kFALSE;
xmin = xmin - range;
range *= 2;
binsize *= 2;
// make sure that the merging will be correct
if ( xmin / binsize - TMath::Floor(xmin / binsize) >= 0.5) {
xmin += 0.5 * binsize;
xmax += 0.5 * binsize; // won't work with a histogram with only one bin, but I don't care
}
}
while (point >= xmax) {
if (ntimes++ > 64)
return kFALSE;
xmax = xmax + range;
range *= 2;
binsize *= 2;
// make sure that the merging will be correct
if ( xmin / binsize - TMath::Floor(xmin / binsize) >= 0.5) {
xmin -= 0.5 * binsize;
xmax -= 0.5 * binsize; // won't work with a histogram with only one bin, but I don't care
}
}
newMin = xmin;
newMax = xmax;
// Info("FindNewAxisLimits", "OldAxis: (%lf, %lf), new: (%lf, %lf), point: %lf",
// axis->GetXmin(), axis->GetXmax(), xmin, xmax, point);
return kTRUE;
}
//______________________________________________________________________________
void TH1::RebinAxis(Axis_t x, const char *ax)
{
// Histogram is resized along ax such that x is in the axis range.
// The new axis limits are recomputed by doubling iteratively
// the current axis range until the specified value x is within the limits.
// The algorithm makes a copy of the histogram, then loops on all bins
// of the old histogram to fill the rebinned histogram.
// Takes into account errors (Sumw2) if any.
// The algorithm works for 1-d, 2-d and 3-d histograms.
// The bit kCanRebin must be set before invoking this function.
// Ex: h->SetBit(TH1::kCanRebin);
if (!TestBit(kCanRebin)) return;
if (TMath::IsNaN(x)) { // x may be a NaN
ResetBit(kCanRebin);
return;
}
char achoice = toupper(ax[0]);
TAxis *axis = &fXaxis;
if (achoice == 'Y') axis = &fYaxis;
if (achoice == 'Z') axis = &fZaxis;
if (axis->GetXmin() >= axis->GetXmax()) return;
if (axis->GetNbins() <= 0) return;
Axis_t xmin, xmax;
if (!FindNewAxisLimits(axis, x, xmin, xmax))
return;
//save a copy of this histogram
TH1 *hold = (TH1*)Clone();
hold->SetDirectory(0);
//set new axis limits
axis->SetLimits(xmin,xmax);
Int_t nbinsx = fXaxis.GetNbins();
Int_t nbinsy = fYaxis.GetNbins();
Int_t nbinsz = fZaxis.GetNbins();
//now loop on all bins and refill
Double_t err,cu;
Axis_t bx,by,bz;
Int_t errors = GetSumw2N();
Int_t ix,iy,iz,ibin,binx,biny,binz,bin;
Reset("ICE"); //reset only Integral, contents and Errors
for (binz=1;binz<=nbinsz;binz++) {
bz = hold->GetZaxis()->GetBinCenter(binz);
iz = fZaxis.FindFixBin(bz);
for (biny=1;biny<=nbinsy;biny++) {
by = hold->GetYaxis()->GetBinCenter(biny);
iy = fYaxis.FindFixBin(by);
for (binx=1;binx<=nbinsx;binx++) {
bx = hold->GetXaxis()->GetBinCenter(binx);
ix = fXaxis.FindFixBin(bx);
bin = hold->GetBin(binx,biny,binz);
ibin= GetBin(ix,iy,iz);
cu = hold->GetBinContent(bin);
AddBinContent(ibin,cu);
if (errors) {
err = hold->GetBinError(bin);
fSumw2.fArray[ibin] += err*err;
}
}
}
}
delete hold;
}
//______________________________________________________________________________
void TH1::RecursiveRemove(TObject *obj)
{
// Recursively remove object from the list of functions
if (fFunctions) {
if (!fFunctions->TestBit(kInvalidObject)) fFunctions->RecursiveRemove(obj);
}
}
//______________________________________________________________________________
void TH1::Scale(Double_t c1)
{
// -*-*-*Multiply this histogram by a constant c1*-*-*-*-*-*-*-*-*
// ========================================
//
// this = c1*this
//
// Note that both contents and errors(if any) are scaled.
// This function uses the services of TH1::Add
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Scale
Double_t ent = fEntries;
Add(this,this,c1,0);
fEntries = ent;
//if contours set, must also scale contours
Int_t ncontours = GetContour();
if (ncontours == 0) return;
Double_t *levels = fContour.GetArray();
for (Int_t i=0;i<ncontours;i++) {
levels[i] *= c1;
}
}
//______________________________________________________________________________
void TH1::SetDefaultBufferSize(Int_t buffersize)
{
// static function to set the default buffer size for automatic histograms.
// When an histogram is created with one of its axis lower limit greater
// or equal to its upper limit, the function SetBuffer is automatically
// called with the default buffer size.
if (buffersize < 0) buffersize = 0;
fgBufferSize = buffersize;
}
//______________________________________________________________________________
void TH1::SetTitle(const char *title)
{
// Change (i.e. set) the title
// if title is of the form "stringt;stringx;stringy;stringz"
// the histogram title is set to stringt,
// the x axis title to stringx, the y axis title to stringy,etc
fTitle = title;
// Decode fTitle. It may contain X, Y and Z titles
TString str1 = fTitle, str2;
Int_t isc = str1.Index(";");
Int_t lns = str1.Length();
if (isc >=0 ) {
fTitle = str1(0,isc);
str1 = str1(isc+1, lns);
isc = str1.Index(";");
if (isc >=0 ) {
str2 = str1(0,isc);
fXaxis.SetTitle(str2.Data());
lns = str1.Length();
str1 = str1(isc+1, lns);
isc = str1.Index(";");
if (isc >=0 ) {
str2 = str1(0,isc);
fYaxis.SetTitle(str2.Data());
lns = str1.Length();
str1 = str1(isc+1, lns);
fZaxis.SetTitle(str1.Data());
} else {
fYaxis.SetTitle(str1.Data());
}
} else {
fXaxis.SetTitle(str1.Data());
}
}
if (gPad && TestBit(kMustCleanup)) gPad->Modified();
}
// -------------------------------------------------------------------------
void TH1::SmoothArray(Int_t nn, Double_t *xx, Int_t ntimes)
{
// smooth array xx, translation of Hbook routine hsmoof.F
// based on algorithm 353QH twice presented by J. Friedman
// in Proc.of the 1974 CERN School of Computing, Norway, 11-24 August, 1974.
Int_t ii, jj, ik, jk, kk, nn1, nn2;
Double_t hh[6] = {0,0,0,0,0,0};
Double_t *yy = new Double_t[nn];
Double_t *zz = new Double_t[nn];
Double_t *rr = new Double_t[nn];
for (Int_t pass=0;pass<ntimes;pass++) {
// first copy original data into temp array
for (ii = 0; ii < nn; ii++) {
yy[ii] = xx[ii];
}
// do 353 i.e. running median 3, 5, and 3 in a single loop
for (kk = 1; kk <= 3; kk++) {
ik = 0;
if (kk == 2) ik = 1;
nn1 = ik + 2;
nn2 = nn - ik - 1;
// do all elements beside the first and last point for median 3
// and first two and last 2 for median 5
for (ii = nn1; ii <= nn2; ii++) {
for (jj = 0; jj < 3; jj++) {
hh[jj] = yy[ii + jj - 1];
}
zz[ii] = TMath::Median(3 + 2*ik, hh);
}
if (kk == 1) { // first median 3
// first point
hh[0] = 3*yy[1] - 2*yy[2];
hh[1] = yy[0];
hh[2] = yy[2];
zz[0] = TMath::Median(3, hh);
// last point
hh[0] = yy[nn - 2];
hh[1] = yy[nn - 1];
hh[2] = 3*yy[nn - 2] - 2*yy[nn - 3];
zz[nn - 1] = TMath::Median(3, hh);
}
if (kk == 2) { // median 5
// first point remains the same
zz[0] = yy[0];
for (ii = 0; ii < 3; ii++) {
hh[ii] = yy[ii];
}
zz[1] = TMath::Median(3, hh);
// last two points
for (ii = 0; ii < 3; ii++) {
hh[ii] = yy[nn +nn2 -1 + ii];
}
zz[nn - 2] = TMath::Median(3, hh);
zz[nn - 1] = yy[nn - 1];
}
}
// quadratic interpolation for flat segments
nn2 = nn2 - 2;
for (ii = nn1; ii <= nn2; ii++) {
if (zz[ii - 1] != zz[ii]) continue;
if (zz[ii] != zz[ii + 1]) continue;
hh[0] = zz[ii - 2] - zz[ii];
hh[1] = zz[ii + 2] - zz[ii];
if (hh[0] * hh[1] < 0) continue;
jk = 0;
if ( TMath::Abs(hh[1]) > TMath::Abs(hh[0]) ) jk = -1;
yy[ii] = -0.5*zz[ii - 2*jk] + zz[ii - jk]/0.75 + zz[ii + 2*jk] /6.;
yy[ii + jk] = 0.5*(zz[ii + 2*jk] - zz[ii - 2*jk]) + zz[ii - jk];
}
// running means
for (ii = 1; ii < nn - 1; ii++) {
rr[ii] = 0.25*yy[ii - 1] + 0.5*yy[ii] + 0.25*yy[ii + 1];
}
rr[0] = yy[0];
rr[nn - 1] = yy[nn - 1];
// now do the same for residuals
for (ii = 0; ii < nn; ii++) {
yy[ii] = xx[ii] - rr[ii];
}
// do 353 i.e. running median 3, 5, and 3 in a single loop
for (kk = 1; kk <= 3; kk++) {
ik = 0;
if (kk == 2) ik = 1;
nn1 = ik + 1;
nn2 = nn - ik - 1;
// do all elements beside the first and last point for median 3
// and first two and last 2 for median 5
for (ii = nn1; ii <= nn2; ii++) {
for (jj = 0; jj < 3; jj++) {
hh[jj] = yy[ii + jj - 1];
}
zz[ii] = TMath::Median(3 + 2*ik, hh);
}
if (kk == 1) { // first median 3
// first point
hh[0] = 3*yy[1] - 2*yy[2];
hh[1] = yy[0];
hh[2] = yy[2];
zz[0] = TMath::Median(3, hh);
// last point
hh[0] = yy[nn - 2];
hh[1] = yy[nn - 1];
hh[2] = 3*yy[nn - 2] - 2*yy[nn - 3];
zz[nn - 1] = TMath::Median(3, hh);
}
if (kk == 2) { // median 5
// first point remains the same
zz[0] = yy[0];
for (ii = 0; ii < 3; ii++) {
hh[ii] = yy[ii];
}
zz[1] = TMath::Median(3, hh);
// last two points
for (ii = 0; ii < 3; ii++) {
hh[ii] = yy[nn - 3 + ii];
}
zz[nn - 2] = TMath::Median(3, hh);
zz[nn - 1] = yy[nn - 1];
}
}
// quadratic interpolation for flat segments
nn2 = nn2 - 1;
for (ii = nn1 + 1; ii <= nn2; ii++) {
if (zz[ii - 1] != zz[ii]) continue;
if (zz[ii] != zz[ii + 1]) continue;
hh[0] = zz[ii - 2] - zz[ii];
hh[1] = zz[ii + 2] - zz[ii];
if (hh[0] * hh[1] < 0) continue;
jk = 0;
if ( TMath::Abs(hh[1]) > TMath::Abs(hh[0]) ) jk = -1;
yy[ii] = -0.5*zz[ii - 2*jk] + zz[ii - jk]/0.75 + zz[ii + 2*jk]/6.;
yy[ii + jk] = 0.5*(zz[ii + 2*jk] - zz[ii - 2*jk]) + zz[ii - jk];
}
// running means
for (ii = 1; ii <= nn - 1; ii++) {
zz[ii] = 0.25*yy[ii - 1] + 0.5*yy[ii] + 0.25*yy[ii + 1];
}
zz[0] = yy[0];
zz[nn - 1] = yy[nn - 1];
// add smoothed xx and smoothed residuals
for (ii = 0; ii < nn; ii++) {
if (xx[ii] < 0) xx[ii] = rr[ii] + zz[ii];
else xx[ii] = TMath::Abs(rr[ii] + zz[ii]);
}
}
delete [] yy;
delete [] zz;
delete [] rr;
}
// ------------------------------------------------------------------------
void TH1::Smooth(Int_t ntimes, Int_t firstbin, Int_t lastbin)
{
// Smooth bin contents of this histogram between firstbin and lastbin.
// (if firstbin=-1 and lastbin=-1 (default) all bins are smoothed.
// bin contents are replaced by their smooth values.
// Errors (if any) are not modified.
// algorithm can only be applied to 1-d histograms
if (fDimension != 1) {
Error("Smooth","Smooth only supported for 1-d histograms");
return;
}
Int_t nbins = fXaxis.GetNbins();
if (firstbin < 0) firstbin = 1;
if (lastbin < 0) lastbin = nbins;
if (lastbin > nbins+1) lastbin = nbins;
nbins = lastbin - firstbin + 1;
Double_t *xx = new Double_t[nbins];
Int_t i;
for (i=0;i<nbins;i++) {
xx[i] = GetBinContent(i+firstbin);
}
TH1::SmoothArray(nbins,xx,ntimes);
for (i=0;i<nbins;i++) {
SetBinContent(i+firstbin,xx[i]);
}
delete [] xx;
if (gPad) gPad->Modified();
}
// ------------------------------------------------------------------------
void TH1::StatOverflows(Bool_t flag)
{
// if flag=kTRUE, underflows and overflows are used by the Fill functions
// in the computation of statistics (mean value, RMS).
// By default, underflows or overflows are not used.
fgStatOverflows = flag;
}
//_______________________________________________________________________
void TH1::Streamer(TBuffer &b)
{
// -*-*-*-*-*-*-*Stream a class object*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
// =====================
if (b.IsReading()) {
UInt_t R__s, R__c;
Version_t R__v = b.ReadVersion(&R__s, &R__c);
if (R__v > 2) {
TH1::Class()->ReadBuffer(b, this, R__v, R__s, R__c);
fXaxis.SetParent(this);
fYaxis.SetParent(this);
fZaxis.SetParent(this);
if (fgAddDirectory && !gROOT->ReadingObject()) {
fDirectory = gDirectory;
if (!gDirectory->GetList()->FindObject(this)) gDirectory->Append(this);
}
ResetBit(kCanDelete);
return;
}
//process old versions before automatic schema evolution
TNamed::Streamer(b);
TAttLine::Streamer(b);
TAttFill::Streamer(b);
TAttMarker::Streamer(b);
b >> fNcells;
fXaxis.Streamer(b);
fYaxis.Streamer(b);
fZaxis.Streamer(b);
fXaxis.SetParent(this);
fYaxis.SetParent(this);
fZaxis.SetParent(this);
b >> fBarOffset;
b >> fBarWidth;
b >> fEntries;
b >> fTsumw;
b >> fTsumw2;
b >> fTsumwx;
b >> fTsumwx2;
if (R__v < 2) {
Float_t maximum, minimum, norm;
Float_t *contour=0;
b >> maximum; fMaximum = maximum;
b >> minimum; fMinimum = minimum;
b >> norm; fNormFactor = norm;
Int_t n = b.ReadArray(contour);
fContour.Set(n);
for (Int_t i=0;i<n;i++) fContour.fArray[i] = contour[i];
delete [] contour;
} else {
b >> fMaximum;
b >> fMinimum;
b >> fNormFactor;
fContour.Streamer(b);
}
fSumw2.Streamer(b);
fOption.Streamer(b);
fFunctions->Delete();
fFunctions->Streamer(b);
if (!gROOT->ReadingObject()) {
fDirectory = gDirectory;
if (!gDirectory->GetList()->FindObject(this)) gDirectory->Append(this);
}
b.CheckByteCount(R__s, R__c, TH1::IsA());
} else {
TH1::Class()->WriteBuffer(b,this);
}
}
//______________________________________________________________________________
void TH1::Print(Option_t *option) const
{
// -*-*-*-*-*Print some global quantities for this histogram*-*-*-*-*-*-*-*
// ===============================================
//
// If option "base" is given, number of bins and ranges are also printed
// If option "range" is given, bin contents and errors are also printed
// for all bins in the current range (default 1-->nbins)
// If option "all" is given, bin contents and errors are also printed
// for all bins including under and overflows.
//
printf( "TH1.Print Name = %s, Entries= %d, Total sum= %g\n",GetName(),Int_t(fEntries),GetSumOfWeights());
TString opt = option;
opt.ToLower();
Int_t all;
if (opt.Contains("all")) all = 0;
else if (opt.Contains("range")) all = 1;
else if (opt.Contains("base")) all = 2;
else return;
Int_t bin, binx, biny, binz;
Int_t firstx=0,lastx=0,firsty=0,lasty=0,firstz=0,lastz=0;
if (all == 0) {
lastx = fXaxis.GetNbins()+1;
if (fDimension > 1) lasty = fYaxis.GetNbins()+1;
if (fDimension > 2) lastz = fZaxis.GetNbins()+1;
} else {
firstx = fXaxis.GetFirst(); lastx = fXaxis.GetLast();
if (fDimension > 1) {firsty = fYaxis.GetFirst(); lasty = fYaxis.GetLast();}
if (fDimension > 2) {firstz = fZaxis.GetFirst(); lastz = fZaxis.GetLast();}
}
if (all== 2) {
printf(" Title = %s\n", GetTitle());
printf(" NbinsX= %d, xmin= %g, xmax=%g", fXaxis.GetNbins(), fXaxis.GetXmin(), fXaxis.GetXmax());
if( fDimension > 1) printf(", NbinsY= %d, ymin= %g, ymax=%g", fYaxis.GetNbins(), fYaxis.GetXmin(), fYaxis.GetXmax());
if( fDimension > 2) printf(", NbinsZ= %d, zmin= %g, zmax=%g", fZaxis.GetNbins(), fZaxis.GetXmin(), fZaxis.GetXmax());
printf("\n");
return;
}
Stat_t w,e;
Axis_t x,y,z;
if (fDimension == 1) {
for (binx=firstx;binx<=lastx;binx++) {
x = fXaxis.GetBinCenter(binx);
w = GetBinContent(binx);
e = GetBinError(binx);
if(fSumw2.fN) printf(" fSumw[%d]=%g, x=%g, error=%g\n",binx,w,x,e);
else printf(" fSumw[%d]=%g, x=%g\n",binx,w,x);
}
}
if (fDimension == 2) {
for (biny=firsty;biny<=lasty;biny++) {
y = fYaxis.GetBinCenter(biny);
for (binx=firstx;binx<=lastx;binx++) {
bin = GetBin(binx,biny);
x = fXaxis.GetBinCenter(binx);
w = GetBinContent(bin);
e = GetBinError(bin);
if(fSumw2.fN) printf(" fSumw[%d][%d]=%g, x=%g, y=%g, error=%g\n",binx,biny,w,x,y,e);
else printf(" fSumw[%d][%d]=%g, x=%g, y=%g\n",binx,biny,w,x,y);
}
}
}
if (fDimension == 3) {
for (binz=firstz;binz<=lastz;binz++) {
z = fZaxis.GetBinCenter(binz);
for (biny=firsty;biny<=lasty;biny++) {
y = fYaxis.GetBinCenter(biny);
for (binx=firstx;binx<=lastx;binx++) {
bin = GetBin(binx,biny,binz);
x = fXaxis.GetBinCenter(binx);
w = GetBinContent(bin);
e = GetBinError(bin);
if(fSumw2.fN) printf(" fSumw[%d][%d][%d]=%g, x=%g, y=%g, z=%g, error=%g\n",binx,biny,binz,w,x,y,z,e);
else printf(" fSumw[%d][%d][%d]=%g, x=%g, y=%g, z=%g\n",binx,biny,binz,w,x,y,z);
}
}
}
}
}
//______________________________________________________________________________
void TH1::Rebuild(Option_t *)
{
// Using the current bin info, recompute the arrays for contents and errors
SetBinsLength();
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::Reset(Option_t *option)
{
// -*-*-*-*-*-*Reset this histogram: contents, errors, etc*-*-*-*-*-*-*-*
// ===========================================
//
// if option "ICE" is specified, resets only Integral, Contents and Errors.
TString opt = option;
opt.ToUpper();
fSumw2.Reset();
if (fIntegral) {delete [] fIntegral; fIntegral = 0;}
if (opt.Contains("ICE")) return;
if (fBuffer) BufferEmpty();
fTsumw = 0;
fTsumw2 = 0;
fTsumwx = 0;
fTsumwx2 = 0;
fEntries = 0;
TObject *stats = fFunctions->FindObject("stats");
fFunctions->Remove(stats);
//special logic to support the case where the same object is
//added multiple times in fFunctions.
//This case happens when the same object is added with different
//drawing modes
TObject *obj;
while ((obj = fFunctions->First())) {
while(fFunctions->Remove(obj));
delete obj;
}
if(stats) fFunctions->Add(stats);
fContour.Set(0);
}
//______________________________________________________________________________
void TH1::SavePrimitive(ofstream &out, Option_t *option)
{
// Save primitive as a C++ statement(s) on output stream out
Bool_t nonEqiX = kFALSE;
Bool_t nonEqiY = kFALSE;
Bool_t nonEqiZ = kFALSE;
Int_t i;
// Check if the histogram has equidistant X bins or not. If not, we
// create an array holding the bins.
if (GetXaxis()->GetXbins()->fN && GetXaxis()->GetXbins()->fArray) {
nonEqiX = kTRUE;
out << " Double_t xAxis[" << GetXaxis()->GetXbins()->fN
<< "] = {";
for (i = 0; i < GetXaxis()->GetXbins()->fN; i++) {
if (i != 0) out << ", ";
out << GetXaxis()->GetXbins()->fArray[i];
}
out << "}; " << endl;
}
// If the histogram is 2 or 3 dimensional, check if the histogram
// has equidistant Y bins or not. If not, we create an array
// holding the bins.
if (fDimension > 1 && GetYaxis()->GetXbins()->fN &&
GetYaxis()->GetXbins()->fArray) {
nonEqiY = kTRUE;
out << " Double_t yAxis[" << GetYaxis()->GetXbins()->fN
<< "] = {";
for (i = 0; i < GetYaxis()->GetXbins()->fN; i++) {
if (i != 0) out << ", ";
out << GetYaxis()->GetXbins()->fArray[i];
}
out << "}; " << endl;
}
// IF the histogram is 3 dimensional, check if the histogram
// has equidistant Z bins or not. If not, we create an array
// holding the bins.
if (fDimension > 2 && GetZaxis()->GetXbins()->fN &&
GetZaxis()->GetXbins()->fArray) {
nonEqiZ = kTRUE;
out << " Double_t zAxis[" << GetZaxis()->GetXbins()->fN
<< "] = {";
for (i = 0; i < GetZaxis()->GetXbins()->fN; i++) {
if (i != 0) out << ", ";
out << GetZaxis()->GetXbins()->fArray[i];
}
out << "}; " << endl;
}
char quote = '"';
out <<" "<<endl;
out <<" "<<"TH1"<<" *";
out << GetName() << " = new " << ClassName() << "(" << quote
<< GetName() << quote << "," << quote<< GetTitle() << quote
<< "," << GetXaxis()->GetNbins();
if (nonEqiX)
out << ", xAxis";
else
out << "," << GetXaxis()->GetXmin()
<< "," << GetXaxis()->GetXmax();
if (fDimension > 1) {
out << "," << GetYaxis()->GetNbins();
if (nonEqiY)
out << ", yAxis";
else
out << "," << GetYaxis()->GetXmin()
<< "," << GetYaxis()->GetXmax();
}
if (fDimension > 2) {
out << "," << GetZaxis()->GetNbins();
if (nonEqiZ)
out << ", zAxis";
else
out << "," << GetZaxis()->GetXmin()
<< "," << GetZaxis()->GetXmax();
}
out << ");" << endl;
// save bin contents
Int_t bin;
for (bin=0;bin<fNcells;bin++) {
Double_t bc = GetBinContent(bin);
if (bc) {
out<<" "<<GetName()<<"->SetBinContent("<<bin<<","<<bc<<");"<<endl;
}
}
// save bin errors
if (fSumw2.fN) {
for (bin=0;bin<fNcells;bin++) {
Double_t be = GetBinError(bin);
if (be) {
out<<" "<<GetName()<<"->SetBinError("<<bin<<","<<be<<");"<<endl;
}
}
}
TH1::SavePrimitiveHelp(out, option);
}
//______________________________________________________________________________
void TH1::SavePrimitiveHelp(ofstream &out, Option_t *option)
{
// helper function for the SavePrimitive functions from TH1
// or classes derived from TH1, eg TProfile, TProfile2D.
char quote = '"';
if (TMath::Abs(GetBarOffset()) > 1e-5) {
out<<" "<<GetName()<<"->SetBarOffset("<<GetBarOffset()<<");"<<endl;
}
if (TMath::Abs(GetBarWidth()-1) > 1e-5) {
out<<" "<<GetName()<<"->SetBarWidth("<<GetBarWidth()<<");"<<endl;
}
if (fMinimum != -1111) {
out<<" "<<GetName()<<"->SetMinimum("<<fMinimum<<");"<<endl;
}
if (fMaximum != -1111) {
out<<" "<<GetName()<<"->SetMaximum("<<fMaximum<<");"<<endl;
}
if (fNormFactor != 0) {
out<<" "<<GetName()<<"->SetNormFactor("<<fNormFactor<<");"<<endl;
}
if (fEntries != 0) {
out<<" "<<GetName()<<"->SetEntries("<<fEntries<<");"<<endl;
}
if (fDirectory == 0) {
out<<" "<<GetName()<<"->SetDirectory(0);"<<endl;
}
if (TestBit(kNoStats)) {
out<<" "<<GetName()<<"->SetStats(0);"<<endl;
}
if (fOption.Length() != 0) {
out<<" "<<GetName()<<"->SetOption("<<quote<<fOption.Data()<<quote<<");"<<endl;
}
// save contour levels
Int_t ncontours = GetContour();
if (ncontours > 0) {
out<<" "<<GetName()<<"->SetContour("<<ncontours<<");"<<endl;
for (Int_t bin=0;bin<ncontours;bin++) {
out<<" "<<GetName()<<"->SetContourLevel("<<bin<<","<<GetContourLevel(bin)<<");"<<endl;
}
}
// save list of functions
TObjOptLink *lnk = (TObjOptLink*)fFunctions->FirstLink();
TObject *obj;
while (lnk) {
obj = lnk->GetObject();
obj->SavePrimitive(out,"nodraw");
if (obj->InheritsFrom("TF1")) {
out<<" "<<GetName()<<"->GetListOfFunctions()->Add("<<obj->GetName()<<");"<<endl;
} else if (obj->InheritsFrom("TPaveStats")) {
out<<" "<<GetName()<<"->GetListOfFunctions()->Add(ptstats);"<<endl;
out<<" ptstats->SetParent("<<GetName()<<"->GetListOfFunctions());"<<endl;
} else {
out<<" "<<GetName()<<"->GetListOfFunctions()->Add("<<obj->GetName()<<","<<quote<<lnk->GetOption()<<quote<<");"<<endl;
}
lnk = (TObjOptLink*)lnk->Next();
}
// save attributes
SaveFillAttributes(out,GetName(),0,1001);
SaveLineAttributes(out,GetName(),1,1,1);
SaveMarkerAttributes(out,GetName(),1,1,1);
fXaxis.SaveAttributes(out,GetName(),"->GetXaxis()");
fYaxis.SaveAttributes(out,GetName(),"->GetYaxis()");
fZaxis.SaveAttributes(out,GetName(),"->GetZaxis()");
TString opt = option;
opt.ToLower();
if (!opt.Contains("nodraw")) {
out<<" "<<GetName()<<"->Draw("
<<quote<<option<<quote<<");"<<endl;
}
}
//______________________________________________________________________________
void TH1::UseCurrentStyle()
{
// Copy current attributes from/to current style
if (gStyle->IsReading()) {
fXaxis.ResetAttAxis("X");
fYaxis.ResetAttAxis("Y");
fZaxis.ResetAttAxis("Z");
SetBarOffset(gStyle->GetBarOffset());
SetBarWidth(gStyle->GetBarWidth());
SetFillColor(gStyle->GetHistFillColor());
SetFillStyle(gStyle->GetHistFillStyle());
SetLineColor(gStyle->GetHistLineColor());
SetLineStyle(gStyle->GetHistLineStyle());
SetLineWidth(gStyle->GetHistLineWidth());
SetMarkerColor(gStyle->GetMarkerColor());
SetMarkerStyle(gStyle->GetMarkerStyle());
SetMarkerSize(gStyle->GetMarkerSize());
Int_t dostat = gStyle->GetOptStat();
if (gStyle->GetOptFit() && !dostat) dostat = 1000000001;
SetStats(dostat);
} else {
gStyle->SetBarOffset(fBarOffset);
gStyle->SetBarWidth(fBarWidth);
gStyle->SetHistFillColor(GetFillColor());
gStyle->SetHistFillStyle(GetFillStyle());
gStyle->SetHistLineColor(GetLineColor());
gStyle->SetHistLineStyle(GetLineStyle());
gStyle->SetHistLineWidth(GetLineWidth());
gStyle->SetMarkerColor(GetMarkerColor());
gStyle->SetMarkerStyle(GetMarkerStyle());
gStyle->SetMarkerSize(GetMarkerSize());
gStyle->SetOptStat(TestBit(kNoStats));
}
}
//______________________________________________________________________________
Double_t TH1::GetMean(Int_t axis) const
{
// For axis = 1,2 or 3 returns the mean value of the histogram along
// X,Y or Z axis.
// For axis = 11, 12, 13 returns the standard error of the mean value
// of the histogram along X, Y or Z axis
//
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
// -*-*-*-*-*-*Return mean value of this histogram along the X axis*-*-*-*-*
// ====================================================
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
if (axis<1 || axis>3&&axis<11 || axis>13) return 0;
Stat_t stats[kNstat];
for (Int_t i=4;i<kNstat;i++) stats[i] = 0;
GetStats(stats);
if (stats[0] == 0) return 0;
if (axis<10){
Int_t ax[3] = {2,4,7};
return stats[ax[axis-1]]/stats[0];
} else {
Double_t rms = GetRMS(axis-10);
return (rms/TMath::Sqrt(stats[0]));
}
}
//______________________________________________________________________________
Double_t TH1::GetMeanError(Int_t axis) const
{
// -*-*-*-*-*-*Return standard error of mean of this histogram along the X axis*-*-*-*-*
// ====================================================
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
// Also note, that although the definition of standard error doesn't include the
// assumption of normality, many uses of this feature implicitly assume it.
return GetMean(axis+10);
}
//______________________________________________________________________________
Double_t TH1::GetRMS(Int_t axis) const
{
// For axis = 1,2 or 3 returns the Sigma value of the histogram along
// X, Y or Z axis
// For axis = 11, 12 or 13 returns the error of RMS estimation along
// X, Y or Z axis for Normal distribution
//
// Note that the mean value/sigma is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
// Note that this function returns the Standard Deviation (Sigma)
// of the distribution (not RMS).
// The Sigma estimate is computed as Sqrt((1/N)*(Sum(x_i-x_mean)^2))
// The name "RMS" was introduced many years ago (Hbook/PAW times).
// We kept the name for continuity.
if (axis<1 || axis>3&&axis<11 || axis>13) return 0;
Stat_t x, rms2, stats[kNstat];
for (Int_t i=4;i<kNstat;i++) stats[i] = 0;
GetStats(stats);
if (stats[0] == 0) return 0;
Int_t ax[3] = {2,4,7};
Int_t axm = ax[axis%10 - 1];
x = stats[axm]/stats[0];
rms2 = TMath::Abs(stats[axm+1]/stats[0] -x*x);
if (axis<10)
return TMath::Sqrt(rms2);
else
return TMath::Sqrt(rms2/(2*stats[0]));
}
//______________________________________________________________________________
Double_t TH1::GetRMSError(Int_t axis) const
{
// Return error of RMS estimation for Normal distribution
//
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
// Value returned is standard deviation of sample standard deviation.
return GetRMS(axis+10);
}
//______________________________________________________________________________
Double_t TH1::GetSkewness(Int_t axis) const
{
//For axis = 1, 2 or 3 returns skewness of the histogram along x, y or z axis.
//For axis = 11, 12 or 13 returns the approximate standard error of skewness
//of the histogram along x, y or z axis
//Note, that since third and fourth moment are not calculated
//at the fill time, skewness and its standard error are computed bin by bin
const TAxis *ax;
if (axis==1 || axis==11) ax = &fXaxis;
else if (axis==2 || axis==12) ax = &fYaxis;
else if (axis==3 || axis==13) ax = &fZaxis;
else {
Error("GetSkewness", "illegal value of parameter");
return 0;
}
if (axis < 10) {
//compute skewness
Double_t x, w, mean, rms, rms3, sum=0;
mean = GetMean(axis);
rms = GetRMS(axis);
rms3 = rms*rms*rms;
Int_t bin;
Double_t np=0;
for (bin=ax->GetFirst(); bin<=ax->GetLast(); bin++){
x = GetBinCenter(bin);
w = GetBinContent(bin);
np+=w;
sum+=w*(x-mean)*(x-mean)*(x-mean);
}
sum/=np*rms3;
return sum;
} else {
//compute standard error of skewness
Int_t nbins = ax->GetNbins();
return TMath::Sqrt(6./nbins);
}
}
//______________________________________________________________________________
Double_t TH1::GetKurtosis(Int_t axis) const
{
//For axis =1, 2 or 3 returns kurtosis of the histogram along x, y or z axis.
//Kurtosis(gaussian(0, 1)) = 0.
//For axis =11, 12 or 13 returns the approximate standard error of kurtosis
//of the histogram along x, y or z axis
//Note, that since third and fourth moment are not calculated
//at the fill time, kurtosis and its standard error are computed bin by bin
const TAxis *ax;
if (axis==1 || axis==11) ax = &fXaxis;
else if (axis==2 || axis==12) ax = &fYaxis;
else if (axis==3 || axis==13) ax = &fZaxis;
else {
Error("GetKurtosis", "illegal value of parameter");
return 0;
}
if (axis < 10){
Double_t x, w, mean, rms, rms4, sum=0;
mean = GetMean(axis);
rms = GetRMS(axis);
rms4 = rms*rms*rms*rms;
Int_t bin;
Double_t np=0;
for (bin=ax->GetFirst(); bin<=ax->GetLast(); bin++){
x = GetBinCenter(bin);
w = GetBinContent(bin);
np+=w;
sum+=w*(x-mean)*(x-mean)*(x-mean)*(x-mean);
}
sum/=np*rms4;
return sum-3;
} else {
Int_t nbins = ax->GetNbins();
return TMath::Sqrt(24./nbins);
}
}
//______________________________________________________________________________
void TH1::GetStats(Stat_t *stats) const
{
// fill the array stats from the contents of this histogram
// The array stats must be correctly dimensionned in the calling program.
// stats[0] = sumw
// stats[1] = sumw2
// stats[2] = sumwx
// stats[3] = sumwx2
//
// If no axis-subrange is specified (via TAxis::SetRange), the array stats
// is simply a copy of the statistics quantities computed at filling time.
// If a sub-range is specified, the function recomputes these quantities
// from the bin contents in the current axis range.
//
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
if (fBuffer) ((TH1*)this)->BufferEmpty();
// Loop on bins (possibly including underflows/overflows)
Int_t bin, binx;
Stat_t w,err;
Axis_t x;
if (fTsumw == 0 || fXaxis.TestBit(TAxis::kAxisRange)) {
for (bin=0;bin<4;bin++) stats[bin] = 0;
for (binx=fXaxis.GetFirst();binx<=fXaxis.GetLast();binx++) {
x = fXaxis.GetBinCenter(binx);
w = TMath::Abs(GetBinContent(binx));
err = TMath::Abs(GetBinError(binx));
stats[0] += w;
stats[1] += err*err;
stats[2] += w*x;
stats[3] += w*x*x;
}
} else {
stats[0] = fTsumw;
stats[1] = fTsumw2;
stats[2] = fTsumwx;
stats[3] = fTsumwx2;
}
}
//______________________________________________________________________________
void TH1::PutStats(Stat_t *stats)
{
// Replace current statistics with the values in array stats
fTsumw = stats[0];
fTsumw2 = stats[1];
fTsumwx = stats[2];
fTsumwx2 = stats[3];
}
//______________________________________________________________________________
Stat_t TH1::GetSumOfWeights() const
{
// -*-*-*-*-*-*Return the sum of weights excluding under/overflows*-*-*-*-*
// ===================================================
Int_t bin,binx,biny,binz;
Stat_t sum =0;
for(binz=1; binz<=fZaxis.GetNbins(); binz++) {
for(biny=1; biny<=fYaxis.GetNbins(); biny++) {
for(binx=1; binx<=fXaxis.GetNbins(); binx++) {
bin = GetBin(binx,biny,binz);
sum += GetBinContent(bin);
}
}
}
return sum;
}
//______________________________________________________________________________
Stat_t TH1::Integral(Option_t *option) const
{
//Return integral of bin contents. Only bins in the bins range are considered.
// By default the integral is computed as the sum of bin contents in the range.
// if option "width" is specified, the integral is the sum of
// the bin contents multiplied by the bin width in x.
return Integral(fXaxis.GetFirst(),fXaxis.GetLast(),option);
}
//______________________________________________________________________________
Stat_t TH1::Integral(Int_t binx1, Int_t binx2, Option_t *option) const
{
//Return integral of bin contents between binx1 and binx2 for a 1-D histogram
// By default the integral is computed as the sum of bin contents in the range.
// if option "width" is specified, the integral is the sum of
// the bin contents multiplied by the bin width in x.
if (binx1 < 0) binx1 = 0;
Stat_t integral = 0;
// - Loop on bins in specified range
TString opt = option;
opt.ToLower();
Bool_t width = kFALSE;
if (opt.Contains("width")) width = kTRUE;
Int_t binx;
for (binx=binx1;binx<=binx2;binx++) {
if (width) integral += GetBinContent(binx)*fXaxis.GetBinWidth(binx);
else integral += GetBinContent(binx);
}
return integral;
}
//______________________________________________________________________________
Double_t TH1::KolmogorovTest(const TH1 *h2, Option_t *option) const
{
// Statistical test of compatibility in shape between
// THIS histogram and h2, using Kolmogorov test.
//
// Default: Ignore under- and overflow bins in comparison
//
// option is a character string to specify options
// "U" include Underflows in test (also for 2-dim)
// "O" include Overflows (also valid for 2-dim)
// "N" include comparison of normalizations
// "D" Put out a line of "Debug" printout
// "M" Return the Maximum Kolmogorov distance instead of prob
// "X" Run the pseudo experiments post-processor with the following procedure:
// make pseudoexperiments based on random values from the parent
// distribution and compare the KS distance of the pseudoexperiment
// to the parent distribution. Bin the KS distances in a histogram,
// and then take the integral of all the KS values above the value
// obtained from the original data to Monte Carlo distribution.
// The number of pseudo-experiments nEXPT is currently fixed at 1000.
// The function returns the integral.
// (thanks to Ben Kilminster to submit this procedure). Note that
// this option "X" is much slower.
//
// The returned function value is the probability of test
// (much less than one means NOT compatible)
//
// Code adapted by Rene Brun from original HBOOK routine HDIFF
//
// NOTE1
// A good description of the Kolmogorov test can be seen at:
// http://www.itl.nist.gov/div898/handbook/eda/section3/eda35g.htm
//
// NOTE2
// see also alternative function TH1::Chi2Test
// The Kolmogorov test is assumed to give better results than Chi2Test
// in case of histograms with low statistics.
//
// NOTE3 (Jan Conrad, Fred James)
// "The returned value PROB is calculated such that it will be
// uniformly distributed between zero and one for compatible histograms,
// provided the data are not binned (or the number of bins is very large
// compared with the number of events). Users who have access to unbinned
// data and wish exact confidence levels should therefore not put their data
// into histograms, but should call directly TMath::KolmogorovTest. On
// the other hand, since TH1 is a convenient way of collecting data and
// saving space, this function has been provided. However, the values of
// PROB for binned data will be shifted slightly higher than expected,
// depending on the effects of the binning. For example, when comparing two
// uniform distributions of 500 events in 100 bins, the values of PROB,
// instead of being exactly uniformly distributed between zero and one, have
// a mean value of about 0.56. We can apply a useful
// rule: As long as the bin width is small compared with any significant
// physical effect (for example the experimental resolution) then the binning
// cannot have an important effect. Therefore, we believe that for all
// practical purposes, the probability value PROB is calculated correctly
// provided the user is aware that:
// 1. The value of PROB should not be expected to have exactly the correct
// distribution for binned data.
// 2. The user is responsible for seeing to it that the bin widths are
// small compared with any physical phenomena of interest.
// 3. The effect of binning (if any) is always to make the value of PROB
// slightly too big. That is, setting an acceptance criterion of (PROB>0.05
// will assure that at most 5% of truly compatible histograms are rejected,
// and usually somewhat less."
TString opt = option;
opt.ToUpper();
Double_t prob = 0;
TH1 *h1 = (TH1*)this;
if (h2 == 0) return 0;
TAxis *axis1 = h1->GetXaxis();
TAxis *axis2 = h2->GetXaxis();
Int_t ncx1 = axis1->GetNbins();
Int_t ncx2 = axis2->GetNbins();
// Check consistency of dimensions
if (h1->GetDimension() != 1 || h2->GetDimension() != 1) {
Error("KolmogorovTest","Histograms must be 1-D\n");
return 0;
}
// Check consistency in number of channels
if (ncx1 != ncx2) {
Error("KolmogorovTest","Number of channels is different, %d and %d\n",ncx1,ncx2);
return 0;
}
// Check consistency in channel edges
Double_t difprec = 1e-5;
Double_t diff1 = TMath::Abs(axis1->GetXmin() - axis2->GetXmin());
Double_t diff2 = TMath::Abs(axis1->GetXmax() - axis2->GetXmax());
if (diff1 > difprec || diff2 > difprec) {
Error("KolmogorovTest","histograms with different binning");
return 0;
}
Bool_t afunc1 = kFALSE;
Bool_t afunc2 = kFALSE;
Double_t sum1 = 0, sum2 = 0;
Double_t ew1, ew2, w1 = 0, w2 = 0;
Int_t bin;
for (bin=1;bin<=ncx1;bin++) {
sum1 += h1->GetBinContent(bin);
sum2 += h2->GetBinContent(bin);
ew1 = h1->GetBinError(bin);
ew2 = h2->GetBinError(bin);
w1 += ew1*ew1;
w2 += ew2*ew2;
}
if (sum1 == 0) {
Error("KolmogorovTest","Histogram1 %s integral is zero\n",h1->GetName());
return 0;
}
if (sum2 == 0) {
Error("KolmogorovTest","Histogram2 %s integral is zero\n",h2->GetName());
return 0;
}
Double_t tsum1 = sum1;
Double_t tsum2 = sum2;
if (opt.Contains("U")) {
tsum1 += h1->GetBinContent(0);
tsum2 += h2->GetBinContent(0);
}
if (opt.Contains("O")) {
tsum1 += h1->GetBinContent(ncx1+1);
tsum2 += h2->GetBinContent(ncx1+1);
}
// Check if histograms are weighted.
// If number of entries = number of channels, probably histograms were
// not filled via Fill(), but via SetBinContent()
Double_t ne1 = h1->GetEntries();
Double_t ne2 = h2->GetEntries();
// look at first histogram
Double_t difsum1 = (ne1-tsum1)/tsum1;
Double_t esum1 = sum1;
if (difsum1 > difprec && Int_t(ne1) != ncx1) {
if (opt.Contains("U") || opt.Contains("O")) {
Warning("KolmogorovTest","U/O option with weighted events for hist:%s\n",h1->GetName());
}
if (h1->GetSumw2N() == 0) {
Warning("KolmogorovTest","Weighted events and no Sumw2, hist:%s\n",h1->GetName());
} else {
esum1 = sum1*sum1/w1; //number of equivalent entries
}
}
// look at second histogram
Double_t difsum2 = (ne2-tsum2)/tsum2;
Double_t esum2 = sum2;
if (difsum2 > difprec && Int_t(ne2) != ncx1) {
if (opt.Contains("U") || opt.Contains("O")) {
Warning("KolmogorovTest","U/O option with weighted events for hist:%s\n",h2->GetName());
}
if (h2->GetSumw2N() == 0) {
Warning("KolmogorovTest","Weighted events and no Sumw2, hist:%s\n",h2->GetName());
} else {
esum2 = sum2*sum2/w2; //number of equivalent entries
}
}
Double_t s1 = 1/tsum1;
Double_t s2 = 1/tsum2;
// Find largest difference for Kolmogorov Test
Double_t dfmax =0, rsum1 = 0, rsum2 = 0;
Int_t first = 1;
Int_t last = ncx1;
if (opt.Contains("U")) first = 0;
if (opt.Contains("O")) last = ncx1+1;
for (bin=first;bin<=last;bin++) {
rsum1 += s1*h1->GetBinContent(bin);
rsum2 += s2*h2->GetBinContent(bin);
dfmax = TMath::Max(dfmax,TMath::Abs(rsum1-rsum2));
}
// Get Kolmogorov probability
Double_t z, prb1=0, prb2=0, prb3=0;
if (afunc1) z = dfmax*TMath::Sqrt(esum2);
else if (afunc2) z = dfmax*TMath::Sqrt(esum1);
else z = dfmax*TMath::Sqrt(esum1*esum2/(esum1+esum2));
prob = TMath::KolmogorovProb(z);
if (opt.Contains("N")) {
// Combine probabilities for shape and normalization,
prb1 = prob;
Double_t resum1 = esum1; if (afunc1) resum1 = 0;
Double_t resum2 = esum2; if (afunc2) resum2 = 0;
Double_t d12 = esum1-esum2;
Double_t chi2 = d12*d12/(resum1+resum2);
prb2 = TMath::Prob(chi2,1);
// see Eadie et al., section 11.6.2
if (prob > 0 && prb2 > 0) prob *= prb2*(1-TMath::Log(prob*prb2));
else prob = 0;
}
// X option. Pseudo-experiments post-processor to determine KS probability
const Int_t nEXPT = 1000;
if (opt.Contains("X")) {
Double_t dSEXPT;
Bool_t addStatus = fgAddDirectory;
fgAddDirectory = kFALSE;
TH1F *hDistValues = new TH1F("hDistValues","KS distances",200,0,1);
TH1 *hExpt = (TH1*)Clone();
fgAddDirectory = addStatus;
// make nEXPT experiments (this should be a parameter)
for (Int_t i=0; i < nEXPT; i++) {
hExpt->Reset();
hExpt->FillRandom(h1,(Int_t)ne2);
dSEXPT = KolmogorovTest(hExpt,"M");
hDistValues->Fill(dSEXPT);
}
prb3 = hDistValues->Integral(hDistValues->FindBin(dfmax),200)/hDistValues->Integral();
delete hDistValues;
delete hExpt;
}
// debug printout
if (opt.Contains("D")) {
printf(" Kolmo Prob h1 = %s, sum1=%g\n",h1->GetName(),sum1);
printf(" Kolmo Prob h2 = %s, sum2=%g\n",h2->GetName(),sum2);
printf(" Kolmo Prob = %g, Max Dist = %g\n",prob,dfmax);
if (opt.Contains("N"))
printf(" Kolmo Prob = %f for shape alone, =%f for normalisation alone\n",prb1,prb2);
if (opt.Contains("X"))
printf(" Kolmo Prob = %f with %d pseudo-experiments\n",prb3,nEXPT);
}
// This numerical error condition should never occur:
if (TMath::Abs(rsum1-1) > 0.002) Warning("KolmogorovTest","Numerical problems with h1=%s\n",h1->GetName());
if (TMath::Abs(rsum2-1) > 0.002) Warning("KolmogorovTest","Numerical problems with h2=%s\n",h2->GetName());
if(opt.Contains("M")) return dfmax;
else if(opt.Contains("X")) return prb3;
else return prob;
}
//______________________________________________________________________________
void TH1::SetContent(const Stat_t *content)
{
// -*-*-*-*-*-*Replace bin contents by the contents of array content*-*-*-*
// =====================================================
Int_t bin;
Stat_t bincontent;
for (bin=0; bin<fNcells; bin++) {
bincontent = *(content + bin);
SetBinContent(bin, bincontent);
}
}
//______________________________________________________________________________
Int_t TH1::GetContour(Double_t *levels)
{
// Return contour values into array levels if pointer levels is non zero
//
// The function returns the number of contour levels.
// see GetContourLevel to return one contour only
//
Int_t nlevels = fContour.fN;
if (levels) {
if (nlevels == 0) {
nlevels = 20;
SetContour(nlevels);
} else {
if (TestBit(kUserContour) == 0) SetContour(nlevels);
}
for (Int_t level=0; level<nlevels; level++) levels[level] = fContour.fArray[level];
}
return nlevels;
}
//______________________________________________________________________________
Double_t TH1::GetContourLevel(Int_t level) const
{
// Return value of contour number level
// see GetContour to return the array of all contour levels
if (level <0 || level >= fContour.fN) return 0;
Double_t zlevel = fContour.fArray[level];
return zlevel;
}
//______________________________________________________________________________
Double_t TH1::GetContourLevelPad(Int_t level) const
{
// Return the value of contour number "level" in Pad coordinates ie: if the Pad
// is in log scale along Z it returns le log of the contour level value.
// see GetContour to return the array of all contour levels
if (level <0 || level >= fContour.fN) return 0;
Double_t zlevel = fContour.fArray[level];
// In case of user defined contours and Pad in log scale along Z,
// fContour.fArray doesn't contain the log of the contour whereas it does
// in case of equidistant contours.
if (gPad && gPad->GetLogz() && TestBit(kUserContour)) {
if (zlevel <= 0) return 0;
zlevel = TMath::Log10(zlevel);
}
return zlevel;
}
//______________________________________________________________________________
void TH1::SetBuffer(Int_t buffersize, Option_t * /*option*/)
{
// set the maximum number of entries to be kept in the buffer
if (fBuffer) {
BufferEmpty();
delete [] fBuffer;
fBuffer = 0;
}
if (buffersize <= 0) {
fBufferSize = 0;
return;
}
if (buffersize < 100) buffersize = 100;
fBufferSize = 1 + buffersize*(fDimension+1);
fBuffer = new Double_t[fBufferSize];
memset(fBuffer,0,8*fBufferSize);
}
//______________________________________________________________________________
void TH1::SetContour(Int_t nlevels, const Double_t *levels)
{
// -*-*-*-*-*-*Set the number and values of contour levels*-*-*-*-*-*-*-*-*
// ===========================================
//
// By default the number of contour levels is set to 20.
//
// if argument levels = 0 or missing, equidistant contours are computed
//
Int_t level;
ResetBit(kUserContour);
if (nlevels <=0 ) {
fContour.Set(0);
return;
}
fContour.Set(nlevels);
// - Contour levels are specified
if (levels) {
SetBit(kUserContour);
for (level=0; level<nlevels; level++) fContour.fArray[level] = levels[level];
} else {
// - contour levels are computed automatically as equidistant contours
Double_t zmin = GetMinimum();
Double_t zmax = GetMaximum();
if ((zmin == zmax) && (zmin != 0)) {
zmax += 0.01*TMath::Abs(zmax);
zmin -= 0.01*TMath::Abs(zmin);
}
Double_t dz = (zmax-zmin)/Double_t(nlevels);
if (gPad && gPad->GetLogz()) {
if (zmax <= 0) return;
if (zmin <= 0) zmin = 0.001*zmax;
zmin = TMath::Log10(zmin);
zmax = TMath::Log10(zmax);
dz = (zmax-zmin)/Double_t(nlevels);
}
for (level=0; level<nlevels; level++) {
fContour.fArray[level] = zmin + dz*Double_t(level);
}
}
}
//______________________________________________________________________________
void TH1::SetContourLevel(Int_t level, Double_t value)
{
// -*-*-*-*-*-*-*-*-*Set value for one contour level*-*-*-*-*-*-*-*-*-*-*-*
// ===============================
if (level <0 || level >= fContour.fN) return;
SetBit(kUserContour);
fContour.fArray[level] = value;
}
//______________________________________________________________________________
Double_t TH1::GetMaximum(Double_t maxval) const
{
// Return maximum value smaller than maxval of bins in the range*-*-*-*-*-*
if (fMaximum != -1111) return fMaximum;
Int_t bin, binx, biny, binz;
Int_t xfirst = fXaxis.GetFirst();
Int_t xlast = fXaxis.GetLast();
Int_t yfirst = fYaxis.GetFirst();
Int_t ylast = fYaxis.GetLast();
Int_t zfirst = fZaxis.GetFirst();
Int_t zlast = fZaxis.GetLast();
Double_t maximum = -FLT_MAX, value;
for (binz=zfirst;binz<=zlast;binz++) {
for (biny=yfirst;biny<=ylast;biny++) {
for (binx=xfirst;binx<=xlast;binx++) {
bin = GetBin(binx,biny,binz);
value = GetBinContent(bin);
if (value > maximum && value < maxval) maximum = value;
}
}
}
return maximum;
}
//______________________________________________________________________________
Int_t TH1::GetMaximumBin() const
{
// -*-*-*-*-*Return location of bin with maximum value in the range*-*
// ======================================================
Int_t locmax, locmay, locmaz;
return GetMaximumBin(locmax, locmay, locmaz);
}
//______________________________________________________________________________
Int_t TH1::GetMaximumBin(Int_t &locmax, Int_t &locmay, Int_t &locmaz) const
{
// -*-*-*-*-*Return location of bin with maximum value in the range*-*
// ======================================================
Int_t bin, binx, biny, binz;
Int_t locm;
Int_t xfirst = fXaxis.GetFirst();
Int_t xlast = fXaxis.GetLast();
Int_t yfirst = fYaxis.GetFirst();
Int_t ylast = fYaxis.GetLast();
Int_t zfirst = fZaxis.GetFirst();
Int_t zlast = fZaxis.GetLast();
Double_t maximum = -FLT_MAX, value;
locm = locmax = locmay = locmaz = 0;
for (binz=zfirst;binz<=zlast;binz++) {
for (biny=yfirst;biny<=ylast;biny++) {
for (binx=xfirst;binx<=xlast;binx++) {
bin = GetBin(binx,biny,binz);
value = GetBinContent(bin);
if (value > maximum) {
maximum = value;
locm = bin;
locmax = binx;
locmay = biny;
locmaz = binz;
}
}
}
}
return locm;
}
//______________________________________________________________________________
Double_t TH1::GetMinimum(Double_t minval) const
{
// Return minimum value greater than minval of bins in the range
if (fMinimum != -1111) return fMinimum;
Int_t bin, binx, biny, binz;
Int_t xfirst = fXaxis.GetFirst();
Int_t xlast = fXaxis.GetLast();
Int_t yfirst = fYaxis.GetFirst();
Int_t ylast = fYaxis.GetLast();
Int_t zfirst = fZaxis.GetFirst();
Int_t zlast = fZaxis.GetLast();
Double_t minimum=FLT_MAX, value;
for (binz=zfirst;binz<=zlast;binz++) {
for (biny=yfirst;biny<=ylast;biny++) {
for (binx=xfirst;binx<=xlast;binx++) {
bin = GetBin(binx,biny,binz);
value = GetBinContent(bin);
if (value < minimum && value > minval) minimum = value;
}
}
}
return minimum;
}
//______________________________________________________________________________
Int_t TH1::GetMinimumBin() const
{
// -*-*-*-*-*Return location of bin with minimum value in the range*-*
// ======================================================
Int_t locmix, locmiy, locmiz;
return GetMinimumBin(locmix, locmiy, locmiz);
}
//______________________________________________________________________________
Int_t TH1::GetMinimumBin(Int_t &locmix, Int_t &locmiy, Int_t &locmiz) const
{
// -*-*-*-*-*Return location of bin with minimum value in the range*-*
// ======================================================
Int_t bin, binx, biny, binz;
Int_t locm;
Int_t xfirst = fXaxis.GetFirst();
Int_t xlast = fXaxis.GetLast();
Int_t yfirst = fYaxis.GetFirst();
Int_t ylast = fYaxis.GetLast();
Int_t zfirst = fZaxis.GetFirst();
Int_t zlast = fZaxis.GetLast();
Double_t minimum = FLT_MAX, value;
locm = locmix = locmiy = locmiz = 0;
for (binz=zfirst;binz<=zlast;binz++) {
for (biny=yfirst;biny<=ylast;biny++) {
for (binx=xfirst;binx<=xlast;binx++) {
bin = GetBin(binx,biny,binz);
value = GetBinContent(bin);
if (value < minimum) {
minimum = value;
locm = bin;
locmix = binx;
locmiy = biny;
locmiz = binz;
}
}
}
}
return locm;
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, Axis_t xmin, Axis_t xmax)
{
// -*-*-*-*-*-*-*Redefine x axis parameters*-*-*-*-*-*-*-*-*-*-*-*
// ===========================
// The X axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
if (GetDimension() != 1) {
Error("SetBins","Operation only valid for 1-d histograms");
return;
}
fXaxis.SetRange(0,0);
fXaxis.Set(nx,xmin,xmax);
fYaxis.Set(1,0,1);
fZaxis.Set(1,0,1);
fNcells = nx+2;
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, const Axis_t *xBins)
{
// -*-*-*-*-*-*-*Redefine x axis parameters with variable bin sizes *-*-*-*-*-*-*-*-*-*
// ===================================================
// The X axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
// xBins is supposed to be of length nx+1
if (GetDimension() != 1) {
Error("SetBins","Operation only valid for 1-d histograms");
return;
}
fXaxis.SetRange(0,0);
fXaxis.Set(nx,xBins);
fYaxis.Set(1,0,1);
fZaxis.Set(1,0,1);
fNcells = nx+2;
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, Axis_t xmin, Axis_t xmax, Int_t ny, Axis_t ymin, Axis_t ymax)
{
// -*-*-*-*-*-*-*Redefine x and y axis parameters*-*-*-*-*-*-*-*-*-*-*-*
// =================================
// The X and Y axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
if (GetDimension() != 2) {
Error("SetBins","Operation only valid for 2-d histograms");
return;
}
fXaxis.SetRange(0,0);
fYaxis.SetRange(0,0);
fXaxis.Set(nx,xmin,xmax);
fYaxis.Set(ny,ymin,ymax);
fZaxis.Set(1,0,1);
fNcells = (nx+2)*(ny+2);
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, const Axis_t *xBins, Int_t ny, const Axis_t *yBins)
{
// -*-*-*-*-*-*-*Redefine x and y axis parameters with variable bin sizes *-*-*-*-*-*-*-*-*
// =========================================================
// The X and Y axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
// xBins is supposed to be of length nx+1, yBins is supposed to be of length ny+1
if (GetDimension() != 2) {
Error("SetBins","Operation only valid for 2-d histograms");
return;
}
fXaxis.SetRange(0,0);
fYaxis.SetRange(0,0);
fXaxis.Set(nx,xBins);
fYaxis.Set(ny,yBins);
fZaxis.Set(1,0,1);
fNcells = (nx+2)*(ny+2);
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, Axis_t xmin, Axis_t xmax, Int_t ny, Axis_t ymin, Axis_t ymax, Int_t nz, Axis_t zmin, Axis_t zmax)
{
// -*-*-*-*-*-*-*Redefine x, y and z axis parameters*-*-*-*-*-*-*-*-*-*-*-*
// ====================================
// The X, Y and Z axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
if (GetDimension() != 3) {
Error("SetBins","Operation only valid for 3-d histograms");
return;
}
fXaxis.SetRange(0,0);
fYaxis.SetRange(0,0);
fZaxis.SetRange(0,0);
fXaxis.Set(nx,xmin,xmax);
fYaxis.Set(ny,ymin,ymax);
fZaxis.Set(nz,zmin,zmax);
fNcells = (nx+2)*(ny+2)*(nz+2);
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetMaximum(Double_t maximum)
{
// -*-*-*-*-*-*-*Set the maximum value for the Y axis*-*-*-*-*-*-*-*-*-*-*-*
// ====================================
// By default the maximum value is automatically set to the maximum
// bin content plus a margin of 10 per cent.
// Use TH1::GetMaximum to find the maximum value of an histogram
// Use TH1::GetMaximumBin to find the bin with the maximum value of an histogram
//
fMaximum = maximum;
}
//______________________________________________________________________________
void TH1::SetMinimum(Double_t minimum)
{
// -*-*-*-*-*-*-*Set the minimum value for the Y axis*-*-*-*-*-*-*-*-*-*-*-*
// ====================================
// By default the minimum value is automatically set to zero if all bin contents
// are positive or the minimum - 10 per cent otherwise.
// Use TH1::GetMinimum to find the minimum value of an histogram
// Use TH1::GetMinimumBin to find the bin with the minimum value of an histogram
//
fMinimum = minimum;
}
//______________________________________________________________________________
void TH1::SetDirectory(TDirectory *dir)
{
// By default when an histogram is created, it is added to the list
// of histogram objects in the current directory in memory.
// Remove reference to this histogram from current directory and add
// reference to new directory dir. dir can be 0 in which case the
// histogram does not belong to any directory.
if (fDirectory == dir) return;
if (fDirectory) fDirectory->GetList()->Remove(this);
fDirectory = dir;
if (fDirectory) fDirectory->GetList()->Add(this);
}
//______________________________________________________________________________
void TH1::SetError(const Stat_t *error)
{
// -*-*-*-*-*-*-*Replace bin errors by values in array error*-*-*-*-*-*-*-*-*
// ===========================================
Int_t bin;
Stat_t binerror;
for (bin=0; bin<fNcells; bin++) {
binerror = error[bin];
SetBinError(bin, binerror);
}
}
//______________________________________________________________________________
void TH1::SetName(const char *name)
{
// Change the name of this histogram
//
// Histograms are named objects in a THashList.
// We must update the hashlist if we change the name
if (fDirectory) fDirectory->GetList()->Remove(this);
fName = name;
if (fDirectory) fDirectory->GetList()->Add(this);
}
//______________________________________________________________________________
void TH1::SetNameTitle(const char *name, const char *title)
{
// Change the name and title of this histogram
//
// Histograms are named objects in a THashList.
// We must update the hashlist if we change the name
if (fDirectory) fDirectory->GetList()->Remove(this);
fName = name;
SetTitle(title);
if (fDirectory) fDirectory->GetList()->Add(this);
}
//______________________________________________________________________________
void TH1::SetStats(Bool_t stats)
{
// -*-*-*-*-*-*-*Set statistics option on/off
// ============================
// By default, the statistics box is drawn.
// The paint options can be selected via gStyle->SetOptStats.
// This function sets/resets the kNoStats bin in the histogram object.
// It has priority over the Style option.
ResetBit(kNoStats);
if (!stats) {
SetBit(kNoStats);
//remove the "stats" object from the list of functions
if (fFunctions) delete fFunctions->FindObject("stats");
}
}
//______________________________________________________________________________
void TH1::Sumw2()
{
// -*-*-*Create structure to store sum of squares of weights*-*-*-*-*-*-*-*
// ===================================================
//
// if histogram is already filled, the sum of squares of weights
// is filled with the existing bin contents
//
// The error per bin will be computed as sqrt(sum of squares of weight)
// for each bin.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (fSumw2.fN) {
Warning("Sumw2","Sum of squares of weights structure already created");
return;
}
fSumw2.Set(fNcells);
for (Int_t bin=0; bin<fNcells; bin++) {
fSumw2.fArray[bin] = GetBinContent(bin);
}
}
//______________________________________________________________________________
TF1 *TH1::GetFunction(const char *name) const
{
// -*-*-*Return pointer to function with name*-*-*-*-*-*-*-*-*-*-*-*-*
// ===================================
//
// Functions such as TH1::Fit store the fitted function in the list of
// functions of this histogram.
return (TF1*)fFunctions->FindObject(name);
}
//______________________________________________________________________________
Stat_t TH1::GetBinError(Int_t bin) const
{
// -*-*-*-*-*Return value of error associated to bin number bin*-*-*-*-*
// ==================================================
//
// if the sum of squares of weights has been defined (via Sumw2),
// this function returns the sqrt(sum of w2).
// otherwise it returns the sqrt(contents) for this bin.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (fBuffer) ((TH1*)this)->BufferEmpty();
if (fSumw2.fN) return TMath::Sqrt(fSumw2.fArray[bin]);
Stat_t error2 = TMath::Abs(GetBinContent(bin));
return TMath::Sqrt(error2);
}
//______________________________________________________________________________
Stat_t TH1::GetBinError(Int_t binx, Int_t biny) const
{
// -*-*-*-*-*Return error of bin number binx, biny
// =====================================
// NB: Function to be called for 2-d histograms only
Int_t bin = GetBin(binx,biny);
return GetBinError(bin);
}
//______________________________________________________________________________
Stat_t TH1::GetBinError(Int_t binx, Int_t biny, Int_t binz) const
{
// -*-*-*-*-*Return error of bin number binx,biny,binz
// =========================================
// NB: Function to be called for 3-d histograms only
Int_t bin = GetBin(binx,biny,binz);
return GetBinError(bin);
}
//______________________________________________________________________________
Stat_t TH1::GetCellContent(Int_t binx, Int_t biny) const
{
// -*-*-*-*-*Return content of bin number binx, biny
// =====================================
// NB: Function to be called for 2-d histograms only
Int_t bin = GetBin(binx,biny);
return GetBinContent(bin);
}
//______________________________________________________________________________
Stat_t TH1::GetCellError(Int_t binx, Int_t biny) const
{
// -*-*-*-*-*Return error of bin number binx, biny
// =====================================
// NB: Function to be called for 2-d histograms only
Int_t bin = GetBin(binx,biny);
return GetBinError(bin);
}
//______________________________________________________________________________
void TH1::SetBinError(Int_t bin, Stat_t error)
{
// see convention for numbering bins in TH1::GetBin
if (!fSumw2.fN) Sumw2();
if (bin <0 || bin>= fSumw2.fN) return;
fSumw2.fArray[bin] = error*error;
}
//______________________________________________________________________________
void TH1::SetBinContent(Int_t binx, Int_t biny, Stat_t content)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
SetBinContent(biny*(fXaxis.GetNbins()+2) + binx,content);
}
//______________________________________________________________________________
void TH1::SetBinContent(Int_t binx, Int_t biny, Int_t binz, Stat_t content)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
if (binz <0 || binz>fZaxis.GetNbins()+1) return;
Int_t bin = GetBin(binx,biny,binz);
SetBinContent(bin,content);
}
//______________________________________________________________________________
void TH1::SetCellContent(Int_t binx, Int_t biny, Stat_t content)
{
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
SetBinContent(biny*(fXaxis.GetNbins()+2) + binx,content);
}
//______________________________________________________________________________
void TH1::SetBinError(Int_t binx, Int_t biny, Stat_t error)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
SetBinError(biny*(fXaxis.GetNbins()+2) + binx,error);
}
//______________________________________________________________________________
void TH1::SetBinError(Int_t binx, Int_t biny, Int_t binz, Stat_t error)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
if (binz <0 || binz>fZaxis.GetNbins()+1) return;
Int_t bin = GetBin(binx,biny,binz);
SetBinError(bin,error);
}
//______________________________________________________________________________
void TH1::SetCellError(Int_t binx, Int_t biny, Stat_t error)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
if (!fSumw2.fN) Sumw2();
Int_t bin = biny*(fXaxis.GetNbins()+2) + binx;
fSumw2.fArray[bin] = error*error;
}
//______________________________________________________________________________
void TH1::SetBinContent(Int_t, Stat_t)
{
// see convention for numbering bins in TH1::GetBin
AbstractMethod("SetBinContent");
}
ClassImp(TH1C)
//______________________________________________________________________________
// TH1C methods
//______________________________________________________________________________
TH1C::TH1C(): TH1(), TArrayC()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1C::TH1C(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type char (one byte per channel)
// ==========================================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayC::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1C::TH1C(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type char (one byte per channel)
// ==========================================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayC::Set(fNcells);
}
//______________________________________________________________________________
TH1C::TH1C(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type char (one byte per channel)
// ==========================================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayC::Set(fNcells);
}
//______________________________________________________________________________
TH1C::~TH1C()
{
}
//______________________________________________________________________________
TH1C::TH1C(const TH1C &h1c) : TH1(), TArrayC()
{
((TH1C&)h1c).Copy(*this);
}
//______________________________________________________________________________
void TH1C::AddBinContent(Int_t bin)
{
// -*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
if (fArray[bin] < 127) fArray[bin]++;
}
//______________________________________________________________________________
void TH1C::AddBinContent(Int_t bin, Stat_t w)
{
// -*-*-*-*-*-*-*-*Increment bin content by w*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
Int_t newval = fArray[bin] + Int_t(w);
if (newval > -128 && newval < 128) {fArray[bin] = Char_t(newval); return;}
if (newval < -127) fArray[bin] = -127;
if (newval > 127) fArray[bin] = 127;
}
//______________________________________________________________________________
void TH1C::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayC::Copy((TH1C&)newth1);
}
//______________________________________________________________________________
TH1 *TH1C::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1C *newth1 = (TH1C*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1C::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1C*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1C::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayC::Reset();
}
//______________________________________________________________________________
void TH1C::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = Char_t (content);
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = Char_t (content);
fEntries++;
}
//______________________________________________________________________________
void TH1C::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayC::Set(n);
}
//______________________________________________________________________________
TH1C& TH1C::operator=(const TH1C &h1)
{
if (this != &h1) ((TH1C&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1C operator*(Double_t c1, const TH1C &h1)
{
TH1C hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1C operator+(const TH1C &h1, const TH1C &h2)
{
TH1C hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1C operator-(const TH1C &h1, const TH1C &h2)
{
TH1C hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1C operator*(const TH1C &h1, const TH1C &h2)
{
TH1C hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1C operator/(const TH1C &h1, const TH1C &h2)
{
TH1C hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
ClassImp(TH1S)
//______________________________________________________________________________
// TH1S methods
//______________________________________________________________________________
TH1S::TH1S(): TH1(), TArrayS()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1S::TH1S(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type short
// ====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayS::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1S::TH1S(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type short
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayS::Set(fNcells);
}
//______________________________________________________________________________
TH1S::TH1S(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type short
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayS::Set(fNcells);
}
//______________________________________________________________________________
TH1S::~TH1S()
{
}
//______________________________________________________________________________
TH1S::TH1S(const TH1S &h1s) : TH1(), TArrayS()
{
((TH1S&)h1s).Copy(*this);
}
//______________________________________________________________________________
void TH1S::AddBinContent(Int_t bin)
{
// -*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
if (fArray[bin] < 32767) fArray[bin]++;
}
//______________________________________________________________________________
void TH1S::AddBinContent(Int_t bin, Stat_t w)
{
// Increment bin content by w
// ==========================
Int_t newval = fArray[bin] + Int_t(w);
if (newval > -32768 && newval < 32768) {fArray[bin] = Short_t(newval); return;}
if (newval < -32767) fArray[bin] = -32767;
if (newval > 32767) fArray[bin] = 32767;
}
//______________________________________________________________________________
void TH1S::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayS::Copy((TH1S&)newth1);
}
//______________________________________________________________________________
TH1 *TH1S::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1S *newth1 = (TH1S*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1S::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1S*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1S::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayS::Reset();
}
//______________________________________________________________________________
void TH1S::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = Short_t (content);
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = Short_t (content);
fEntries++;
}
//______________________________________________________________________________
void TH1S::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayS::Set(n);
}
//______________________________________________________________________________
TH1S& TH1S::operator=(const TH1S &h1)
{
if (this != &h1) ((TH1S&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1S operator*(Double_t c1, const TH1S &h1)
{
TH1S hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1S operator+(const TH1S &h1, const TH1S &h2)
{
TH1S hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1S operator-(const TH1S &h1, const TH1S &h2)
{
TH1S hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1S operator*(const TH1S &h1, const TH1S &h2)
{
TH1S hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1S operator/(const TH1S &h1, const TH1S &h2)
{
TH1S hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
ClassImp(TH1I)
//______________________________________________________________________________
// TH1I methods
//______________________________________________________________________________
TH1I::TH1I(): TH1(), TArrayI()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1I::TH1I(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type integer
// ====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayI::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1I::TH1I(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type integer
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayI::Set(fNcells);
}
//______________________________________________________________________________
TH1I::TH1I(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type integer
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayI::Set(fNcells);
}
//______________________________________________________________________________
TH1I::~TH1I()
{
}
//______________________________________________________________________________
TH1I::TH1I(const TH1I &h1i) : TH1(), TArrayI()
{
((TH1I&)h1i).Copy(*this);
}
//______________________________________________________________________________
void TH1I::AddBinContent(Int_t bin)
{
// -*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
if (fArray[bin] < 2147483647) fArray[bin]++;
}
//______________________________________________________________________________
void TH1I::AddBinContent(Int_t bin, Stat_t w)
{
// Increment bin content by w
// ==========================
Int_t newval = fArray[bin] + Int_t(w);
if (newval > -2147483647 && newval < 2147483647) {fArray[bin] = Int_t(newval); return;}
if (newval < -2147483647) fArray[bin] = -2147483647;
if (newval > 2147483647) fArray[bin] = 2147483647;
}
//______________________________________________________________________________
void TH1I::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayI::Copy((TH1I&)newth1);
}
//______________________________________________________________________________
TH1 *TH1I::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1I *newth1 = (TH1I*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1I::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1I*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1I::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayI::Reset();
}
//______________________________________________________________________________
void TH1I::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = Int_t (content);
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = Int_t (content);
fEntries++;
}
//______________________________________________________________________________
void TH1I::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayI::Set(n);
}
//______________________________________________________________________________
TH1I& TH1I::operator=(const TH1I &h1)
{
if (this != &h1) ((TH1I&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1I operator*(Double_t c1, const TH1I &h1)
{
TH1I hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1I operator+(const TH1I &h1, const TH1I &h2)
{
TH1I hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1I operator-(const TH1I &h1, const TH1I &h2)
{
TH1I hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1I operator*(const TH1I &h1, const TH1I &h2)
{
TH1I hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1I operator/(const TH1I &h1, const TH1I &h2)
{
TH1I hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
ClassImp(TH1F)
//______________________________________________________________________________
// TH1F methods
//______________________________________________________________________________
TH1F::TH1F(): TH1(), TArrayF()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1F::TH1F(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type float
// ====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayF::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1F::TH1F(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type float
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayF::Set(fNcells);
}
//______________________________________________________________________________
TH1F::TH1F(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type float
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayF::Set(fNcells);
}
//______________________________________________________________________________
TH1F::TH1F(const TVectorF &v)
: TH1("TVectorF","",v.GetNrows(),0,v.GetNrows())
{
// Create a histogram from a TVectorF
// by default the histogram name is "TVectorF" and title = ""
TArrayF::Set(fNcells);
fDimension = 1;
for (Int_t i=0;i<v.GetNrows();i++) {
SetBinContent(i+1,v(i));
}
TArrayF::Set(fNcells);
}
//______________________________________________________________________________
TH1F::TH1F(const TH1F &h) : TH1(), TArrayF()
{
((TH1F&)h).Copy(*this);
}
//______________________________________________________________________________
TH1F::~TH1F()
{
}
//______________________________________________________________________________
void TH1F::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayF::Copy((TH1F&)newth1);
}
//______________________________________________________________________________
TH1 *TH1F::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1F *newth1 = (TH1F*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1F::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1F*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1F::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayF::Reset();
}
//______________________________________________________________________________
void TH1F::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = Float_t (content);
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = Float_t (content);
fEntries++;
}
//______________________________________________________________________________
void TH1F::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayF::Set(n);
}
//______________________________________________________________________________
TH1F& TH1F::operator=(const TH1F &h1)
{
if (this != &h1) ((TH1F&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1F operator*(Double_t c1, const TH1F &h1)
{
TH1F hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1F operator+(const TH1F &h1, const TH1F &h2)
{
TH1F hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1F operator-(const TH1F &h1, const TH1F &h2)
{
TH1F hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1F operator*(const TH1F &h1, const TH1F &h2)
{
TH1F hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1F operator/(const TH1F &h1, const TH1F &h2)
{
TH1F hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
ClassImp(TH1D)
//______________________________________________________________________________
// TH1D methods
//______________________________________________________________________________
TH1D::TH1D(): TH1(), TArrayD()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1D::TH1D(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type double
// =====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayD::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1D::TH1D(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type double
// =====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayD::Set(fNcells);
}
//______________________________________________________________________________
TH1D::TH1D(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type double
// =====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayD::Set(fNcells);
}
//______________________________________________________________________________
TH1D::TH1D(const TVectorD &v)
: TH1("TVectorD","",v.GetNrows(),0,v.GetNrows())
{
// Create a histogram from a TVectorD
// by default the histogram name is "TVectorD" and title = ""
TArrayD::Set(fNcells);
fDimension = 1;
for (Int_t i=0;i<v.GetNrows();i++) {
SetBinContent(i+1,v(i));
}
TArrayD::Set(fNcells);
}
//______________________________________________________________________________
TH1D::~TH1D()
{
}
//______________________________________________________________________________
TH1D::TH1D(const TH1D &h1d) : TH1(), TArrayD()
{
((TH1D&)h1d).Copy(*this);
}
//______________________________________________________________________________
void TH1D::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayD::Copy((TH1D&)newth1);
}
//______________________________________________________________________________
TH1 *TH1D::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1D *newth1 = (TH1D*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1D::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1D*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1D::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayD::Reset();
}
//______________________________________________________________________________
void TH1D::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = content;
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = content;
fEntries++;
}
//______________________________________________________________________________
void TH1D::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayD::Set(n);
}
//______________________________________________________________________________
TH1D& TH1D::operator=(const TH1D &h1)
{
if (this != &h1) ((TH1D&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1D operator*(Double_t c1, const TH1D &h1)
{
TH1D hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1D operator+(const TH1D &h1, const TH1D &h2)
{
TH1D hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1D operator-(const TH1D &h1, const TH1D &h2)
{
TH1D hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1D operator*(const TH1D &h1, const TH1D &h2)
{
TH1D hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1D operator/(const TH1D &h1, const TH1D &h2)
{
TH1D hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1 *R__H(Int_t hid)
{
//return pointer to histogram with name
// hid if id >=0
// h_id if id <0
char hname[20];
if(hid >= 0) sprintf(hname,"h%d",hid);
else sprintf(hname,"h_%d",hid);
return (TH1*)gDirectory->Get(hname);
}
//______________________________________________________________________________
TH1 *R__H(const char * hname)
{
//return pointer to histogram with name hname
return (TH1*)gDirectory->Get(hname);
}
ROOT page - Class index - Class Hierarchy - Top of the page
This page has been automatically generated. If you have any comments or suggestions about the page layout send a mail to ROOT support, or contact the developers with any questions or problems regarding ROOT.
 */
//
TF1 *gF1=0; //left for back compatibility (use TVirtualFitter::GetUserFunc instead)
const Int_t kNstat = 11;
Int_t TH1::fgBufferSize = 1000;
Bool_t TH1::fgAddDirectory = kTRUE;
Bool_t TH1::fgStatOverflows= kFALSE;
extern void H1InitGaus();
extern void H1InitExpo();
extern void H1InitPolynom();
extern void H1LeastSquareFit(Int_t n, Int_t m, Double_t *a);
extern void H1LeastSquareLinearFit(Int_t ndata, Double_t &a0, Double_t &a1, Int_t &ifail);
extern void H1LeastSquareSeqnd(Int_t n, Double_t *a, Int_t idim, Int_t &ifail, Int_t k, Double_t *b);
ClassImp(TH1)
//______________________________________________________________________________
TH1::TH1(): TNamed(), TAttLine(), TAttFill(), TAttMarker()
{
// -*-*-*-*-*-*-*-*-*Histogram default constructor*-*-*-*-*-*-*-*-*-*-*-*-*
// =============================
fDirectory = 0;
fFunctions = new TList;
fNcells = 0;
fIntegral = 0;
fPainter = 0;
fEntries = 0;
fNormFactor = 0;
fTsumw = fTsumw2=fTsumwx=fTsumwx2=0;
fMaximum = -1111;
fMinimum = -1111;
fBufferSize = 0;
fBuffer = 0;
fXaxis.SetName("xaxis");
fYaxis.SetName("yaxis");
fZaxis.SetName("zaxis");
fXaxis.SetParent(this);
fYaxis.SetParent(this);
fZaxis.SetParent(this);
UseCurrentStyle();
}
//______________________________________________________________________________
TH1::~TH1()
{
// -*-*-*-*-*-*-*-*-*Histogram default destructor*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ============================
//TH1 *junk = 0;
//junk->SetLineColor(0);
if (!TestBit(kNotDeleted)) return;
if (fIntegral) {delete [] fIntegral; fIntegral = 0;}
if (fBuffer) {delete [] fBuffer; fBuffer = 0;}
if (fFunctions) {
fFunctions->SetBit(kInvalidObject);
TObject *obj;
//special logic to support the case where the same object is
//added multiple times in fFunctions.
//This case happens when the same object is added with different
//drawing modes
//In the loop below we must be careful with objects (eg TCutG) that may
// have been added to the list of functions of several histograms
//and may have been already deleted.
while ((obj = fFunctions->First())) {
while(fFunctions->Remove(obj));
if (!obj->TestBit(kNotDeleted)) break;
delete obj;
}
delete fFunctions;
}
if (fDirectory) {
if (!fDirectory->TestBit(TDirectory::kCloseDirectory))
fDirectory->GetList()->Remove(this);
}
fFunctions = 0;
fDirectory = 0;
delete fPainter;
}
//______________________________________________________________________________
TH1::TH1(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
:TNamed(name,title), TAttLine(), TAttFill(), TAttMarker()
{
// -*-*-*-*-*-*-*Normal constructor for fix bin size histograms*-*-*-*-*-*-*
// ==============================================
//
// Creates the main histogram structure:
// name : name of histogram (avoid blanks)
// title : histogram title
// if title is of the form "stringt;stringx;stringy;stringz"
// the histogram title is set to stringt,
// the x axis title to stringy, the y axis title to stringy,etc
// nbins : number of bins
// xlow : low edge of first bin
// xup : upper edge of last bin (not included in last bin)
//
// When an histogram is created, it is automatically added to the list
// of special objects in the current directory.
// To find the pointer to this histogram in the current directory
// by its name, do:
// TH1F *h1 = (TH1F*)gDirectory->FindObject(name);
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Build();
if (nbins <= 0) nbins = 1;
fXaxis.Set(nbins,xlow,xup);
fNcells = fXaxis.GetNbins()+2;
}
//______________________________________________________________________________
TH1::TH1(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
:TNamed(name,title), TAttLine(), TAttFill(), TAttMarker()
{
// -*-*-*-*-*Normal constructor for variable bin size histograms*-*-*-*-*-*-*
// ===================================================
//
// Creates the main histogram structure:
// name : name of histogram (avoid blanks)
// title : histogram title
// if title is of the form "stringt;stringx;stringy;stringz"
// the histogram title is set to stringt,
// the x axis title to stringy, the y axis title to stringy,etc
// nbins : number of bins
// xbins : array of low-edges for each bin
// This is an array of size nbins+1
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Build();
if (nbins <= 0) nbins = 1;
if (xbins) fXaxis.Set(nbins,xbins);
else fXaxis.Set(nbins,0,1);
fNcells = fXaxis.GetNbins()+2;
}
//______________________________________________________________________________
TH1::TH1(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
:TNamed(name,title), TAttLine(), TAttFill(), TAttMarker()
{
// -*-*-*-*-*Normal constructor for variable bin size histograms*-*-*-*-*-*-*
// ===================================================
//
// Creates the main histogram structure:
// name : name of histogram (avoid blanks)
// title : histogram title
// if title is of the form "stringt;stringx;stringy;stringz"
// the histogram title is set to stringt,
// the x axis title to stringy, the y axis title to stringy,etc
// nbins : number of bins
// xbins : array of low-edges for each bin
// This is an array of size nbins+1
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Build();
if (nbins <= 0) nbins = 1;
if (xbins) fXaxis.Set(nbins,xbins);
else fXaxis.Set(nbins,0,1);
fNcells = fXaxis.GetNbins()+2;
}
//______________________________________________________________________________
TH1::TH1(const TH1 &h) : TNamed(), TAttLine(), TAttFill(), TAttMarker()
{
// Copy constructor.
// The list of functions is not copied. (Use Clone if needed)
Copy((TObject&)h);
}
//______________________________________________________________________________
Bool_t TH1::AddDirectoryStatus()
{
//static function: cannot be inlined on Windows/NT
return fgAddDirectory;
}
//______________________________________________________________________________
void TH1::Browse(TBrowser *b)
{
Draw(b ? b->GetDrawOption() : "");
gPad->Update();
}
//______________________________________________________________________________
void TH1::Build()
{
// -*-*-*-*-*-*-*-*Creates histogram basic data structure*-*-*-*-*-*-*-*-*-*
// ======================================
fDirectory = 0;
fPainter = 0;
fIntegral = 0;
fEntries = 0;
fNormFactor = 0;
fTsumw = fTsumw2=fTsumwx=fTsumwx2=0;
fMaximum = -1111;
fMinimum = -1111;
fBufferSize = 0;
fBuffer = 0;
fXaxis.SetName("xaxis");
fYaxis.SetName("yaxis");
fZaxis.SetName("zaxis");
fYaxis.Set(1,0.,1.);
fZaxis.Set(1,0.,1.);
fXaxis.SetParent(this);
fYaxis.SetParent(this);
fZaxis.SetParent(this);
SetTitle(fTitle.Data());
fFunctions = new TList;
UseCurrentStyle();
if (fgAddDirectory && gDirectory) {
if (!gDirectory->GetList()) {
Warning("Build","Current directory is not a valid directory");
return;
}
TH1 *hold = (TH1*)gDirectory->GetList()->FindObject(GetName());
if (hold) {
Warning("Build","Replacing existing histogram: %s (Potential memory leak).",GetName());
gDirectory->GetList()->Remove(hold);
hold->SetDirectory(0);
// delete hold;
}
gDirectory->Append(this);
fDirectory = gDirectory;
}
}
//______________________________________________________________________________
void TH1::Add(TF1 *f1, Double_t c1, Option_t *option)
{
// Performs the operation: this = this + c1*f1
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
//
// By default, the function is computed at the centre of the bin.
// if option "I" is specified (1-d histogram only), the integral of the
// function in each bin is used instead of the value of the function at
// the centre of the bin.
// Only bins inside the function range are recomputed.
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Add
if (!f1) {
Error("Add","Attempt to add a non-existing function");
return;
}
TString opt = option;
opt.ToLower();
Bool_t integral = kFALSE;
if (opt.Contains("i") && fDimension ==1) integral = kTRUE;
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// - Add statistics
Stat_t s1[10];
Int_t i;
for (i=0;i<10;i++) {s1[i] = 0;}
PutStats(s1);
SetMinimum();
SetMaximum();
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu=0;
Double_t xx[3];
Double_t *params = 0;
f1->InitArgs(xx,params);
for (binz=0;binz<=nbinsz+1;binz++) {
xx[2] = fZaxis.GetBinCenter(binz);
for (biny=0;biny<=nbinsy+1;biny++) {
xx[1] = fYaxis.GetBinCenter(biny);
for (binx=0;binx<=nbinsx+1;binx++) {
xx[0] = fXaxis.GetBinCenter(binx);
if (!f1->IsInside(xx)) continue;
TF1::RejectPoint(kFALSE);
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
if (integral) {
xx[0] = fXaxis.GetBinLowEdge(binx);
cu = c1*f1->EvalPar(xx);
cu += c1*f1->Integral(fXaxis.GetBinLowEdge(binx),fXaxis.GetBinUpEdge(binx))*fXaxis.GetBinWidth(binx);
} else {
cu = c1*f1->EvalPar(xx);
}
if (TF1::RejectedPoint()) continue;
Double_t error1 = GetBinError(bin);
AddBinContent(bin,cu);
if (fSumw2.fN) {
//errors are unchanged: error on f1 assumed 0
fSumw2.fArray[bin] = error1*error1;
}
}
}
}
}
//______________________________________________________________________________
void TH1::Add(const TH1 *h1, Double_t c1)
{
// Performs the operation: this = this + c1*h1
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
// Note that if h1 has Sumw2 set, Sumw2 is automatically called for this
// if not already set.
//
// IMPORTANT NOTE1: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Add
//
// IMPORTANT NOTE2: if h1 has a normalisation factor, the normalisation factor
// is used , ie this = this + c1*factor*h1
// Use the other TH1::Add function if you do not want this feature
if (!h1) {
Error("Add","Attempt to add a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()) {
Error("Add","Attempt to add histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Add","Attempt to add histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 has Sumw2 set
if (fSumw2.fN == 0 && h1->GetSumw2N() != 0) Sumw2();
// - Add statistics
fEntries += c1*h1->GetEntries();
Stat_t s1[kNstat], s2[kNstat];
Int_t i;
for (i=0;i<kNstat;i++) {s1[i] = s2[i] = 0;}
GetStats(s1);
h1->GetStats(s2);
for (i=0;i<kNstat;i++) {
if (i == 1) s1[i] += c1*c1*s2[i];
else s1[i] += c1*s2[i];
}
PutStats(s1);
SetMinimum();
SetMaximum();
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu;
Double_t factor =1;
if (h1->GetNormFactor() != 0) factor = h1->GetNormFactor()/h1->GetSumOfWeights();;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
cu = c1*factor*h1->GetBinContent(bin);
AddBinContent(bin,cu);
if (fSumw2.fN) {
Double_t error1 = factor*h1->GetBinError(bin);
fSumw2.fArray[bin] += c1*c1*error1*error1;
}
}
}
}
}
//______________________________________________________________________________
void TH1::Add(const TH1 *h1, const TH1 *h2, Double_t c1, Double_t c2)
{
// -*-*-*Replace contents of this histogram by the addition of h1 and h2*-*-*
// ===============================================================
//
// this = c1*h1 + c2*h2
// if errors are defined (see TH1::Sumw2), errors are also recalculated
// Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this
// if not already set.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Add
if (!h1 || !h2) {
Error("Add","Attempt to add a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()
|| nbinsx != h2->GetNbinsX() || nbinsy != h2->GetNbinsY() || nbinsz != h2->GetNbinsZ()) {
Error("Add","Attempt to add histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Add","Attempt to add histograms with different axis limits");
}
if (fXaxis.GetXmin() != h2->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h2->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h2->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h2->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h2->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h2->fZaxis.GetXmax()) {
Warning("Add","Attempt to add histograms::Add with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 or h2 have Sumw2 set
if (fSumw2.fN == 0 && (h1->GetSumw2N() != 0 || h2->GetSumw2N() != 0)) Sumw2();
// - Add statistics
Double_t nEntries = c1*h1->GetEntries() + c2*h2->GetEntries();
Stat_t s1[kNstat], s2[kNstat], s3[kNstat];
Int_t i;
for (i=0;i<kNstat;i++) {s1[i] = s2[i] = s3[i] = 0;}
h1->GetStats(s1);
h2->GetStats(s2);
for (i=0;i<kNstat;i++) {
if (i == 1) s3[i] = c1*c1*s1[i] + c2*c2*s2[i];
else s3[i] = c1*s1[i] + c2*s2[i];
}
PutStats(s3);
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
cu = c1*h1->GetBinContent(bin)+ c2*h2->GetBinContent(bin);
SetBinContent(bin,cu);
if (fSumw2.fN) {
Double_t error1 = h1->GetBinError(bin);
Double_t error2 = h2->GetBinError(bin);
fSumw2.fArray[bin] = c1*c1*error1*error1 + c2*c2*error2*error2;
}
}
}
}
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::AddBinContent(Int_t)
{
// -*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
AbstractMethod("AddBinContent");
}
//______________________________________________________________________________
void TH1::AddBinContent(Int_t, Stat_t)
{
// -*-*-*-*-*-*-*-*Increment bin content by a weight w*-*-*-*-*-*-*-*-*-*-*
// ===================================
AbstractMethod("AddBinContent");
}
//______________________________________________________________________________
void TH1::AddDirectory(Bool_t add)
{
// Sets the flag controlling the automatic add of histograms in memory
//
// By default (fAddDirectory = kTRUE), histograms are automatically added
// to the list of objects in memory.
// Note that one histogram can be removed from its support directory
// by calling h->SetDirectory(0) or h->SetDirectory(dir) to add it
// to the list of objects in the directory dir.
//
// NOTE that this is a static function. To call it, use;
// TH1::AddDirectory
fgAddDirectory = add;
}
//______________________________________________________________________________
Int_t TH1::BufferEmpty(Int_t action)
{
// Fill histogram with all entries in the buffer.
// action = -1 histogram is reset and refilled from the buffer (called by THistPainter::Paint)
// action = 0 histogram is filled from the buffer
// action = 1 histogram is filled and buffer is deleted
// The buffer is automatically deleted when the number of entries
// in the buffer is greater than the number of entries in the histogram
// do we need to compute the bin size?
if (!fBuffer) return 0;
Int_t nbentries = (Int_t)fBuffer[0];
if (!nbentries) return 0;
Double_t *buffer = fBuffer;
if (nbentries < 0) {
if (action == 0) return 0;
nbentries = -nbentries;
fBuffer=0;
Reset();
fBuffer = buffer;
}
if (TestBit(kCanRebin) || (fXaxis.GetXmax() <= fXaxis.GetXmin())) {
//find min, max of entries in buffer
Double_t xmin = fBuffer[2];
Double_t xmax = xmin;
for (Int_t i=1;i<nbentries;i++) {
Double_t x = fBuffer[2*i+2];
if (x < xmin) xmin = x;
if (x > xmax) xmax = x;
}
if (fXaxis.GetXmax() <= fXaxis.GetXmin()) {
THLimitsFinder::GetLimitsFinder()->FindGoodLimits(this,xmin,xmax);
} else {
fBuffer = 0;
Int_t keep = fBufferSize; fBufferSize = 0;
if (xmin < fXaxis.GetXmin()) RebinAxis(xmin,"X");
if (xmax >= fXaxis.GetXmax()) RebinAxis(xmax,"X");
fBuffer = buffer;
fBufferSize = keep;
}
}
FillN(nbentries,&fBuffer[2],&fBuffer[1],2);
if (action > 0) { delete [] fBuffer; fBuffer = 0; fBufferSize = 0;}
else {
if (nbentries == (Int_t)fEntries) fBuffer[0] = -nbentries;
else fBuffer[0] = 0;
}
return nbentries;
}
//______________________________________________________________________________
Int_t TH1::BufferFill(Axis_t x, Stat_t w)
{
// accumulate arguments in buffer. When buffer is full, empty the buffer
// fBuffer[0] = number of entries in buffer
// fBuffer[1] = w of first entry
// fBuffer[2] = x of first entry
if (!fBuffer) return -2;
Int_t nbentries = (Int_t)fBuffer[0];
if (nbentries < 0) {
nbentries = -nbentries;
fBuffer[0] = nbentries;
if (fEntries > 0) {
Double_t *buffer = fBuffer; fBuffer=0;
Reset();
fBuffer = buffer;
}
}
if (2*nbentries+2 >= fBufferSize) {
BufferEmpty(1);
return Fill(x,w);
}
fBuffer[2*nbentries+1] = w;
fBuffer[2*nbentries+2] = x;
fBuffer[0] += 1;
return -2;
}
//______________________________________________________________________________
Double_t TH1::Chi2Test(const TH1 *h, Option_t *option, Int_t constraint) const
{
//The Chi2 (Pearson's) test for differences between h and this histogram.
//a small value of prob indicates a significant difference between the distributions
//
//if the data was collected in such a way that the number of entries
//in the first histogram is necessarily equal to the number of entries
//in the second, the parameter _constraint_ must be made 1. Default is 0.
//any additional constraints on the data lower the number of degrees of freedom
//(i.e. increase constraint to more positive values) in accordance with
//their number
//
///options:
// "O" : overflows included
// "U" : underflows included
// by default underflows and overflows are not included
//
// "P" : print information about number of degrees of freedom and the value of chi2
// "Chi2" : the function returns the Chisquare instead of the probability
// "Chi2/ndf" : the function returns the Chi2/ndf
// if none of the options "Chi2" or "Chi2/ndf" is specified, the function returns
// the Pearson test, ie probability.
//
// algorithm taken from "Numerical Recipes in C++"
// implementation by Anna Kreshuk
//
// A good description of the Chi2test can be seen at:
// http://www.itl.nist.gov/div898/handbook/eda/section3/eda35f.htm
// See also TH1::KolmogorovTest (including NOTE2)
Int_t i, i_start, i_end;
TString opt = option;
opt.ToUpper();
TAxis *axis1 = this->GetXaxis();
TAxis *axis2 = h->GetXaxis();
Int_t nbins1 = axis1->GetNbins();
Int_t nbins2 = axis2->GetNbins();
//check dimensions
if (this->GetDimension()!=1 || h->GetDimension()!=1){
Error("Chi2Test","for 1-d only");
return 0;
}
//check number of channels
if (nbins1 != nbins2){
Error("Chi2Test","different number of channels");
return 0;
}
//see options
i_start = 1;
i_end = nbins1;
Int_t ndf = nbins1-constraint;
if(opt.Contains("O")) {
i_end = nbins1+1;
ndf++;
}
if(opt.Contains("U")) {
i_start = 0;
ndf++;
}
//Compute the normalisation factor
Double_t sum1=0, sum2=0;
for (i=i_start; i<=i_end; i++){
sum1 += this->GetBinContent(i);
sum2 += h->GetBinContent(i);
}
//check that the histograms are not empty
if (sum1 == 0 || sum2 == 0){
Error("Chi2Test","one of the histograms is empty");
return 0;
}
Double_t chsq = 0;
Double_t bin1, bin2, err1, err2, temp;
for (i=i_start; i<=i_end; i++){
bin1 = this->GetBinContent(i)/sum1;
bin2 = h->GetBinContent(i)/sum2;
if (bin1 ==0 && bin2==0){
--ndf; //no data means one less degree of freedom
} else {
temp = bin1-bin2;
err1=this->GetBinError(i);
err2=h->GetBinError(i);
if (err1 == 0 && err2 == 0){
Error("Chi2Test", "bins with non-zero content and zero error");
return 0;
}
err1*=err1;
err2*=err2;
err1/=sum1*sum1;
err2/=sum2*sum2;
chsq+=temp*temp/(err1+err2);
}
}
Double_t prob = TMath::Prob(0.5*chsq, Int_t(0.5*ndf));
if (opt.Contains("P")){
Printf("Chi2 = %f, Prob = %g, NDF = %d\n", chsq,prob,ndf);
}
if (opt.Contains("CHI2/NDF")){
if (ndf == 0) return 0;
return chsq/ndf;
}
if (opt.Contains("CHI2")){
return chsq;
}
return prob;
}
//______________________________________________________________________________
Double_t TH1::ComputeIntegral()
{
// Compute integral (cumulative sum of bins)
// The result stored in fIntegral is used by the GetRandom functions.
// This function is automatically called by GetRandom when the fIntegral
// array does not exist or when the number of entries in the histogram
// has changed since the previous call to GetRandom.
// The resulting integral is normalized to 1
Int_t bin, binx, biny, binz, ibin;
// delete previously computed integral (if any)
if (fIntegral) delete [] fIntegral;
// - Allocate space to store the integral and compute integral
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
Int_t nxy = nbinsx*nbinsy;
Int_t nbins = nxy*nbinsz;
fIntegral = new Double_t[nbins+2];
ibin = 0;
fIntegral[ibin] = 0;
for (binz=1;binz<=nbinsz;binz++) {
for (biny=1;biny<=nbinsy;biny++) {
for (binx=1;binx<=nbinsx;binx++) {
ibin++;
bin = GetBin(binx, biny, binz);
fIntegral[ibin] = fIntegral[ibin-1] + GetBinContent(bin);
}
}
}
// - Normalize integral to 1
if (fIntegral[nbins] == 0 ) {
Error("ComputeIntegral", "Integral = zero"); return 0;
}
for (bin=1;bin<=nbins;bin++) fIntegral[bin] /= fIntegral[nbins];
fIntegral[nbins+1] = fEntries;
return fIntegral[nbins];
}
//______________________________________________________________________________
Double_t *TH1::GetIntegral()
{
// Return a pointer to the array of bins integral.
// if the pointer fIntegral is null, TH1::ComputeIntegral is called
if (fIntegral) ComputeIntegral();
return fIntegral;
}
//______________________________________________________________________________
void TH1::Copy(TObject &obj) const
{
// -*-*-*-*-*Copy this histogram structure to newth1*-*-*-*-*-*-*-*-*-*-*-*
// =======================================
//
// Note that this function does not copy the list of associated functions.
// Use TObJect::Clone to make a full copy of an histogram.
if (((TH1&)obj).fDirectory) {
// We are likely to change the hash value of this object
// with TNamed::Copy, to keep things correct, we need to
// clean up its existing entries.
((TH1&)obj).fDirectory->GetList()->Remove(&obj);
((TH1&)obj).fDirectory = 0;
}
TNamed::Copy(obj);
((TH1&)obj).fDimension = fDimension;
((TH1&)obj).fNormFactor= fNormFactor;
((TH1&)obj).fEntries = fEntries;
((TH1&)obj).fNcells = fNcells;
((TH1&)obj).fBarOffset = fBarOffset;
((TH1&)obj).fBarWidth = fBarWidth;
((TH1&)obj).fTsumw = fTsumw;
((TH1&)obj).fTsumw2 = fTsumw2;
((TH1&)obj).fTsumwx = fTsumwx;
((TH1&)obj).fTsumwx2 = fTsumwx2;
((TH1&)obj).fMaximum = fMaximum;
((TH1&)obj).fMinimum = fMinimum;
((TH1&)obj).fOption = fOption;
((TH1&)obj).fBuffer = 0;
((TH1&)obj).fBufferSize= fBufferSize;
if (fBuffer) {
Double_t *buf = new Double_t[fBufferSize];
for (Int_t i=0;i<fBufferSize;i++) buf[i] = fBuffer[i];
((TH1&)obj).fBuffer = buf;
}
TAttLine::Copy(((TH1&)obj));
TAttFill::Copy(((TH1&)obj));
TAttMarker::Copy(((TH1&)obj));
fXaxis.Copy(((TH1&)obj).fXaxis);
fYaxis.Copy(((TH1&)obj).fYaxis);
fZaxis.Copy(((TH1&)obj).fZaxis);
((TH1&)obj).fXaxis.SetParent(&obj);
((TH1&)obj).fYaxis.SetParent(&obj);
((TH1&)obj).fZaxis.SetParent(&obj);
fContour.Copy(((TH1&)obj).fContour);
fSumw2.Copy(((TH1&)obj).fSumw2);
// fFunctions->Copy(((TH1&)obj).fFunctions);
if (fgAddDirectory && gDirectory) {
gDirectory->Append(&obj);
((TH1&)obj).fDirectory = gDirectory;
}
}
//______________________________________________________________________________
Int_t TH1::DistancetoPrimitive(Int_t px, Int_t py)
{
// -*-*-*-*-*-*-*-*-*Compute distance from point px,py to a line*-*-*-*-*-*
// ===========================================
// Compute the closest distance of approach from point px,py to elements
// of an histogram.
// The distance is computed in pixels units.
//
// Algorithm:
// Currently, this simple model computes the distance from the mouse
// to the histogram contour only.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (!fPainter) return 9999;
return fPainter->DistancetoPrimitive(px,py);
}
//______________________________________________________________________________
void TH1::Divide(TF1 *f1, Double_t c1)
{
// Performs the operation: this = this/(c1*f1)
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
//
// Only bins inside the function range are recomputed.
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Divide
if (!f1) {
Error("Add","Attempt to divide by a non-existing function");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// - Add statistics
Double_t nEntries = fEntries;
Stat_t s1[10];
Int_t i;
for (i=0;i<10;i++) {s1[i] = 0;}
PutStats(s1);
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu,w;
Double_t xx[3];
Double_t *params = 0;
f1->InitArgs(xx,params);
for (binz=0;binz<=nbinsz+1;binz++) {
xx[2] = fZaxis.GetBinCenter(binz);
for (biny=0;biny<=nbinsy+1;biny++) {
xx[1] = fYaxis.GetBinCenter(biny);
for (binx=0;binx<=nbinsx+1;binx++) {
xx[0] = fXaxis.GetBinCenter(binx);
if (!f1->IsInside(xx)) continue;
TF1::RejectPoint(kFALSE);
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
Double_t error1 = GetBinError(bin);
cu = c1*f1->EvalPar(xx);
if (TF1::RejectedPoint()) continue;
if (cu) w = GetBinContent(bin)/cu;
else w = 0;
SetBinContent(bin,w);
if (fSumw2.fN) {
if (cu != 0) fSumw2.fArray[bin] = error1*error1/(cu*cu);
else fSumw2.fArray[bin] = 0;
}
}
}
}
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Divide(const TH1 *h1)
{
// -*-*-*-*-*-*-*-*-*Divide this histogram by h1*-*-*-*-*-*-*-*-*-*-*-*-*
// ===========================
//
// this = this/h1
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
// Note that if h1 has Sumw2 set, Sumw2 is automatically called for this
// if not already set.
// The resulting errors are calculated assuming uncorrelated histograms.
// See the other TH1::Divide that gives the possibility to optionaly
// compute Binomial errors.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Scale
if (!h1) {
Error("Divide","Attempt to divide by a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()) {
Error("Divide","Attempt to divide histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Divide","Attempt to divide histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 has Sumw2 set
if (fSumw2.fN == 0 && h1->GetSumw2N() != 0) Sumw2();
// - Reset statistics
Double_t nEntries = fEntries;
fEntries = fTsumw = 0;
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t c0,c1,w;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = GetBin(binx,biny,binz);
c0 = GetBinContent(bin);
c1 = h1->GetBinContent(bin);
if (c1) w = c0/c1;
else w = 0;
SetBinContent(bin,w);
fEntries++;
if (fSumw2.fN) {
Double_t e0 = GetBinError(bin);
Double_t e1 = h1->GetBinError(bin);
Double_t c12= c1*c1;
if (!c1) { fSumw2.fArray[bin] = 0; continue;}
fSumw2.fArray[bin] = (e0*e0*c1*c1 + e1*e1*c0*c0)/(c12*c12);
}
}
}
}
Stat_t s[kNstat];
GetStats(s);
PutStats(s);
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Divide(const TH1 *h1, const TH1 *h2, Double_t c1, Double_t c2, Option_t *option)
{
// -*-*-*Replace contents of this histogram by the division of h1 by h2*-*-*
// ==============================================================
//
// this = c1*h1/(c2*h2)
//
// if errors are defined (see TH1::Sumw2), errors are also recalculated
// Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this
// if not already set.
// The resulting errors are calculated assuming uncorrelated histograms.
// However, if option ="B" is specified, Binomial errors are computed.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Divide
TString opt = option;
opt.ToLower();
Bool_t binomial = kFALSE;
if (opt.Contains("b")) binomial = kTRUE;
if (!h1 || !h2) {
Error("Divide","Attempt to divide by a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()
|| nbinsx != h2->GetNbinsX() || nbinsy != h2->GetNbinsY() || nbinsz != h2->GetNbinsZ()) {
Error("Divide","Attempt to divide histograms with different number of bins");
return;
}
if (!c2) {
Error("Divide","Coefficient of dividing histogram cannot be zero");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Divide","Attempt to divide histograms with different axis limits");
}
if (fXaxis.GetXmin() != h2->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h2->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h2->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h2->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h2->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h2->fZaxis.GetXmax()) {
Warning("Divide","Attempt to divide histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 or h2 have Sumw2 set
if (fSumw2.fN == 0 && (h1->GetSumw2N() != 0 || h2->GetSumw2N() != 0)) Sumw2();
// - Reset statistics
Double_t nEntries = fEntries;
fEntries = fTsumw = 0;
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t b1,b2,w,d1,d2;
d1 = c1*c1;
d2 = c2*c2;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
b1 = h1->GetBinContent(bin);
b2 = h2->GetBinContent(bin);
if (b2) w = c1*b1/(c2*b2);
else w = 0;
SetBinContent(bin,w);
fEntries++;
if (fSumw2.fN) {
Double_t e1 = h1->GetBinError(bin);
Double_t e2 = h2->GetBinError(bin);
Double_t b22= b2*b2*d2;
if (!b2) { fSumw2.fArray[bin] = 0; continue;}
if (binomial) {
if (b1 != b2) {
//fSumw2.fArray[bin] = TMath::Abs(w*(1-w)/(c2*b2));//this is the formula in Hbook/Hoper1
fSumw2.fArray[bin] = TMath::Abs(w*(1-w)/b2);
} else {
//in case b1=b2 use a simplification of the special algorithm
//from TGraphAsymmErrors::BayesDivide calling Efficiency, etc
Double_t too_low = 0;
Double_t too_high = 1;
Double_t integral;
Double_t a = b1+1;
Double_t x;
for (Int_t loop=0; loop<20; loop++) {
x = 0.5*(too_high + too_low);
Double_t bt = TMath::Exp(TMath::LnGamma(a+1)-TMath::LnGamma(a)+a*log(x)+log(1-x));
if (x < (a+1.0)/(a+3.0)) integral = 1 - bt*TMath::BetaCf(x,a,1)/a;
else integral = bt*TMath::BetaCf(1-x,1,a);
if (integral > 0.683) too_low = x;
else too_high = x;
}
fSumw2.fArray[bin] = (1-x)*(1-x)/4;
}
} else {
fSumw2.fArray[bin] = d1*d2*(e1*e1*b2*b2 + e2*e2*b1*b1)/(b22*b22);
}
}
}
}
}
Stat_t s[kNstat];
GetStats(s);
PutStats(s);
if (nEntries == 0) nEntries = h1->GetEntries();
if (nEntries == 0) nEntries = 1;
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Draw(Option_t *option)
{
// -*-*-*-*-*-*-*-*-*Draw this histogram with options*-*-*-*-*-*-*-*-*-*-*-*
// ================================
//
// Histograms are drawn via the THistPainter class. Each histogram has
// a pointer to its own painter (to be usable in a multithreaded program).
// The same histogram can be drawn with different options in different pads.
// When an histogram drawn in a pad is deleted, the histogram is
// automatically removed from the pad or pads where it was drawn.
// If an histogram is drawn in a pad, then filled again, the new status
// of the histogram will be automatically shown in the pad next time
// the pad is updated. One does not need to redraw the histogram.
// To draw the current version of an histogram in a pad, one can use
// h->DrawCopy();
// This makes a clone of the histogram. Once the clone is drawn, the original
// histogram may be modified or deleted without affecting the aspect of the
// clone.
// By default, TH1::Draw clears the current pad.
//
// One can use TH1::SetMaximum and TH1::SetMinimum to force a particular
// value for the maximum or the minimum scale on the plot.
//
// TH1::UseCurrentStyle can be used to change all histogram graphics
// attributes to correspond to the current selected style.
// This function must be called for each histogram.
// In case one reads and draws many histograms from a file, one can force
// the histograms to inherit automatically the current graphics style
// by calling before gROOT->ForceStyle();
//
// See THistPainter::Paint for a description of all the drawing options
// =======================
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TString opt = option;
opt.ToLower();
if (gPad) {
if (!gPad->IsEditable()) (gROOT->GetMakeDefCanvas())();
if (!opt.Contains("same")) {
//the following statement is necessary in case one attempts to draw
//a temporary histogram already in the current pad
if (TestBit(kCanDelete)) gPad->GetListOfPrimitives()->Remove(this);
gPad->Clear();
}
}
AppendPad(opt.Data());
}
//______________________________________________________________________________
TH1 *TH1::DrawCopy(Option_t *) const
{
// -*-*-*-*-*Copy this histogram and Draw in the current pad*-*-*-*-*-*-*-*
// ===============================================
//
// Once the histogram is drawn into the pad, any further modification
// using graphics input will be made on the copy of the histogram,
// and not to the original object.
//
// See Draw for the list of options
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
AbstractMethod("DrawCopy");
return 0;
}
//______________________________________________________________________________
TH1 *TH1::DrawNormalized(Option_t *option, Double_t norm) const
{
// Draw a normalized copy of this histogram.
//
// A clone of this histogram is normalized to norm and drawn with option.
// A pointer to the normalized histogram is returned.
// The contents of the histogram copy are scaled such that the new
// sum of weights (excluding under and overflow) is equal to norm.
// Note that the returned normalized histogram is not added to the list
// of histograms in the current directory in memory.
// It is the user's responsability to delete this histogram.
// The kCanDelete bit is set for the returned object. If a pad containing
// this copy is cleared, the histogram will be automatically deleted.
//
// See Draw for the list of options
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Double_t sum = GetSumOfWeights();
if (sum == 0) {
Error("DrawNormalized","Sum of weights is null. Cannot normalized histogram: %s",GetName());
return 0;
}
Bool_t addStatus = TH1::AddDirectoryStatus();
TH1::AddDirectory(kFALSE);
TH1 *h = (TH1*)Clone();
h->SetBit(kCanDelete);
h->Scale(norm/sum);
h->Draw(option);
TH1::AddDirectory(addStatus);
return h;
}
//______________________________________________________________________________
void TH1::DrawPanel()
{
// -*-*-*-*-*Display a panel with all histogram drawing options*-*-*-*-*-*
// ==================================================
//
// See class TDrawPanelHist for example
if (!fPainter) {Draw(); if (gPad) gPad->Update();}
if (fPainter) fPainter->DrawPanel();
}
//______________________________________________________________________________
void TH1::Eval(TF1 *f1, Option_t *option)
{
// -*-*-*Evaluate function f1 at the center of bins of this histogram-*-*-*-*
// ============================================================
//
// If option "R" is specified, the function is evaluated only
// for the bins included in the function range.
// If option "A" is specified, the value of the function is added to the
// existing bin contents
// If option "S" is specified, the value of the function is used to
// generate a value, distributed according to the Poisson
// distribution, with f1 as the mean.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Double_t x[3];
Int_t range,stat,add,bin,binx,biny,binz,nbinsx, nbinsy, nbinsz;
if (!f1) return;
Double_t fu;
Double_t e=0;
TString opt = option;
opt.ToLower();
if (opt.Contains("a")) add = 1;
else add = 0;
if (opt.Contains("s")) stat = 1;
else stat = 0;
if (opt.Contains("r")) range = 1;
else range = 0;
nbinsx = fXaxis.GetNbins();
nbinsy = fYaxis.GetNbins();
nbinsz = fZaxis.GetNbins();
if (!add) Reset();
for (binz=1;binz<=nbinsz;binz++) {
x[2] = fZaxis.GetBinCenter(binz);
for (biny=1;biny<=nbinsy;biny++) {
x[1] = fYaxis.GetBinCenter(biny);
for (binx=1;binx<=nbinsx;binx++) {
bin = GetBin(binx,biny,binz);
x[0] = fXaxis.GetBinCenter(binx);
if (range && !f1->IsInside(x)) continue;
fu = f1->Eval(x[0],x[1],x[2]);
if (stat) fu = gRandom->PoissonD(fu);
if (fSumw2.fN) e = fSumw2.fArray[bin];
AddBinContent(bin,fu);
if (fSumw2.fN) fSumw2.fArray[bin] = e+ TMath::Abs(fu);
}
}
}
}
//______________________________________________________________________________
void TH1::ExecuteEvent(Int_t event, Int_t px, Int_t py)
{
// -*-*-*-*-*-*-*-*-*Execute action corresponding to one event*-*-*-*
// =========================================
// This member function is called when a histogram is clicked with the locator
//
// If Left button clicked on the bin top value, then the content of this bin
// is modified according to the new position of the mouse when it is released.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (fPainter) fPainter->ExecuteEvent(event, px, py);
}
//______________________________________________________________________________
Int_t TH1::Fill(Axis_t x)
{
// -*-*-*-*-*-*-*-*Increment bin with abscissa X by 1*-*-*-*-*-*-*-*-*-*-*
// ==================================
//
// if x is less than the low-edge of the first bin, the Underflow bin is incremented
// if x is greater than the upper edge of last bin, the Overflow bin is incremented
//
// If the storage of the sum of squares of weights has been triggered,
// via the function Sumw2, then the sum of the squares of weights is incremented
// by 1 in the bin corresponding to x.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (fBuffer) return BufferFill(x,1);
Int_t bin;
fEntries++;
bin =fXaxis.FindBin(x);
AddBinContent(bin);
if (fSumw2.fN) ++fSumw2.fArray[bin];
if (bin == 0 || bin > fXaxis.GetNbins()) {
if (!fgStatOverflows) return -1;
}
++fTsumw;
++fTsumw2;
fTsumwx += x;
fTsumwx2 += x*x;
return bin;
}
//______________________________________________________________________________
Int_t TH1::Fill(Axis_t x, Stat_t w)
{
// -*-*-*-*-*-*Increment bin with abscissa X with a weight w*-*-*-*-*-*-*-*
// =============================================
//
// if x is less than the low-edge of the first bin, the Underflow bin is incremented
// if x is greater than the upper edge of last bin, the Overflow bin is incremented
//
// If the storage of the sum of squares of weights has been triggered,
// via the function Sumw2, then the sum of the squares of weights is incremented
// by w^2 in the bin corresponding to x.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (fBuffer) return BufferFill(x,w);
Int_t bin;
fEntries++;
bin =fXaxis.FindBin(x);
AddBinContent(bin, w);
if (fSumw2.fN) fSumw2.fArray[bin] += w*w;
if (bin == 0 || bin > fXaxis.GetNbins()) {
if (!fgStatOverflows) return -1;
}
Stat_t z= (w > 0 ? w : -w);
fTsumw += z;
fTsumw2 += z*z;
fTsumwx += z*x;
fTsumwx2 += z*x*x;
return bin;
}
//______________________________________________________________________________
Int_t TH1::Fill(const char *namex, Stat_t w)
{
// Increment bin with namex with a weight w
//
// if x is less than the low-edge of the first bin, the Underflow bin is incremented
// if x is greater than the upper edge of last bin, the Overflow bin is incremented
//
// If the storage of the sum of squares of weights has been triggered,
// via the function Sumw2, then the sum of the squares of weights is incremented
// by w^2 in the bin corresponding to x.
//
Int_t bin;
fEntries++;
bin =fXaxis.FindBin(namex);
AddBinContent(bin, w);
if (fSumw2.fN) fSumw2.fArray[bin] += w*w;
if (bin == 0 || bin > fXaxis.GetNbins()) return -1;
Axis_t x = fXaxis.GetBinCenter(bin);
Stat_t z= (w > 0 ? w : -w);
fTsumw += z;
fTsumw2 += z*z;
fTsumwx += z*x;
fTsumwx2 += z*x*x;
return bin;
}
//______________________________________________________________________________
void TH1::FillN(Int_t ntimes, const Axis_t *x, const Double_t *w, Int_t stride)
{
// -*-*-*-*-*-*Fill this histogram with an array x and weights w*-*-*-*-*
// =================================================
//
// ntimes: number of entries in arrays x and w (array size must be ntimes*stride)
// x: array of values to be histogrammed
// w: array of weighs
// stride: step size through arrays x and w
//
// If the storage of the sum of squares of weights has been triggered,
// via the function Sumw2, then the sum of the squares of weights is incremented
// by w[i]^2 in the bin corresponding to x[i].
// if w is NULL each entry is assumed a weight=1
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t bin,i;
fEntries += ntimes;
Double_t ww = 1;
Int_t nbins = fXaxis.GetNbins();
ntimes *= stride;
for (i=0;i<ntimes;i+=stride) {
bin =fXaxis.FindBin(x[i]);
if (w) ww = w[i];
AddBinContent(bin, ww);
if (fSumw2.fN) fSumw2.fArray[bin] += ww*ww;
if (bin == 0 || bin > nbins) {
if (!fgStatOverflows) continue;
}
Stat_t z= (ww > 0 ? ww : -ww);
fTsumw += z;
fTsumw2 += z*z;
fTsumwx += z*x[i];
fTsumwx2 += z*x[i]*x[i];
}
}
//______________________________________________________________________________
void TH1::FillRandom(const char *fname, Int_t ntimes)
{
// -*-*-*-*-*Fill histogram following distribution in function fname*-*-*-*
// =======================================================
//
// The distribution contained in the function fname (TF1) is integrated
// over the channel contents.
// It is normalized to 1.
// Getting one random number implies:
// - Generating a random number between 0 and 1 (say r1)
// - Look in which bin in the normalized integral r1 corresponds to
// - Fill histogram channel
// ntimes random numbers are generated
//
// One can also call TF1::GetRandom to get a random variate from a function.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-**-*-*-*-*-*-*-*
Int_t bin, binx, ibin, loop;
Double_t r1, x, xv[1];
// - Search for fname in the list of ROOT defined functions
TF1 *f1 = (TF1*)gROOT->GetFunction(fname);
if (!f1) { Error("FillRandom", "Unknown function: %s",fname); return; }
// - Allocate temporary space to store the integral and compute integral
Int_t nbinsx = GetNbinsX();
Double_t *integral = new Double_t[nbinsx+1];
ibin = 0;
integral[ibin] = 0;
for (binx=1;binx<=nbinsx;binx++) {
xv[0] = fXaxis.GetBinCenter(binx);
ibin++;
Double_t fval = f1->Eval(xv[0]);
integral[ibin] = integral[ibin-1] + TMath::Abs(fval)*fXaxis.GetBinWidth(binx);
}
// - Normalize integral to 1
if (integral[nbinsx] == 0 ) {
Error("FillRandom", "Integral = zero"); return;
}
for (bin=1;bin<=nbinsx;bin++) integral[bin] /= integral[nbinsx];
// --------------Start main loop ntimes
for (loop=0;loop<ntimes;loop++) {
r1 = gRandom->Rndm(loop);
ibin = TMath::BinarySearch(nbinsx,&integral[0],r1);
binx = 1 + ibin;
//x = fXaxis.GetBinCenter(binx); //this is not OK when SetBuffer is used
x = fXaxis.GetBinLowEdge(ibin+1)
+fXaxis.GetBinWidth(ibin+1)*(r1-integral[ibin])/(integral[ibin+1] - integral[ibin]);
Fill(x, 1.);
}
delete [] integral;
}
//______________________________________________________________________________
void TH1::FillRandom(TH1 *h, Int_t ntimes)
{
// -*-*-*-*-*Fill histogram following distribution in histogram h*-*-*-*
// ====================================================
//
// The distribution contained in the histogram h (TH1) is integrated
// over the channel contents.
// It is normalized to 1.
// Getting one random number implies:
// - Generating a random number between 0 and 1 (say r1)
// - Look in which bin in the normalized integral r1 corresponds to
// - Fill histogram channel
// ntimes random numbers are generated
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-**-*-*-*-*-*-*-*
if (!h) { Error("FillRandom", "Null histogram"); return; }
if (fDimension != h->GetDimension()) {
Error("FillRandom", "Histograms with different dimensions"); return;
}
if (h->ComputeIntegral() == 0) return;
Int_t loop;
Axis_t x;
for (loop=0;loop<ntimes;loop++) {
x = h->GetRandom();
Fill(x);
}
}
//______________________________________________________________________________
Int_t TH1::FindBin(Axis_t x, Axis_t y, Axis_t z)
{
// -*-*-*-*Return Global bin number corresponding to x,y,z*-*-*-*-*-*-*
// ===============================================
//
// 2-D and 3-D histograms are represented with a one dimensional
// structure.
// This has the advantage that all existing functions, such as
// GetBinContent, GetBinError, GetBinFunction work for all dimensions.
// See also TH1::GetBin
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (GetDimension() < 2) {
return fXaxis.FindBin(x);
}
if (GetDimension() < 3) {
Int_t nx = fXaxis.GetNbins()+2;
Int_t binx = fXaxis.FindBin(x);
Int_t biny = fYaxis.FindBin(y);
return binx + nx*biny;
}
if (GetDimension() < 4) {
Int_t nx = fXaxis.GetNbins()+2;
Int_t ny = fYaxis.GetNbins()+2;
Int_t binx = fXaxis.FindBin(x);
Int_t biny = fYaxis.FindBin(y);
Int_t binz = fZaxis.FindBin(z);
return binx + nx*(biny +ny*binz);
}
return -1;
}
//______________________________________________________________________________
TObject *TH1::FindObject(const char *name) const
{
// search object named name in the list of functions
if (fFunctions) return fFunctions->FindObject(name);
return 0;
}
//______________________________________________________________________________
TObject *TH1::FindObject(const TObject *obj) const
{
// search object obj in the list of functions
if (fFunctions) return fFunctions->FindObject(obj);
return 0;
}
//______________________________________________________________________________
Int_t TH1::Fit(const char *fname ,Option_t *option ,Option_t *goption, Axis_t xxmin, Axis_t xxmax)
{
// Fit histogram with function fname
// =================================
// fname is the name of an already predefined function created by TF1 or TF2
// Predefined functions such as gaus, expo and poln are automatically
// created by ROOT.
// fname can also be a formula, accepted by the linear fitter (linear parts divided
// by "++" sign), for example "x++sin(x)" for fitting "[0]*x+[1]*sin(x)"
//
// This function finds a pointer to the TF1 object with name fname
// and calls TH1::Fit(TF1 *f1,...)
char *linear;
linear= (char*)strstr(fname, "++");
TF1 *f1=0;
TF2 *f2=0;
TF3 *f3=0;
Int_t ndim=GetDimension();
if (linear){
if (ndim<2){
f1=new TF1(fname, fname, xxmin, xxmax);
return Fit(f1,option,goption,xxmin,xxmax);
}
else if (ndim<3){
f2=new TF2(fname, fname);
return Fit(f2,option,goption,xxmin,xxmax);
}
else{
f3=new TF3(fname, fname);
return Fit(f3,option,goption,xxmin,xxmax);
}
}
else{
f1 = (TF1*)gROOT->GetFunction(fname);
if (!f1) { Printf("Unknown function: %s",fname); return -1; }
return Fit(f1,option,goption,xxmin,xxmax);
}
}
//______________________________________________________________________________
Int_t TH1::Fit(TF1 *f1 ,Option_t *option ,Option_t *goption, Axis_t xxmin, Axis_t xxmax)
{
// Fit histogram with function f1
// ==============================
//
// Fit this histogram with function f1.
//
// The list of fit options is given in parameter option.
// option = "W" Set all errors to 1
// = "I" Use integral of function in bin instead of value at bin center
// = "L" Use Loglikelihood method (default is chisquare method)
// = "LL" Use Loglikelihood method and bin contents are not integers)
// = "U" Use a User specified fitting algorithm (via SetFCN)
// = "Q" Quiet mode (minimum printing)
// = "V" Verbose mode (default is between Q and V)
// = "E" Perform better Errors estimation using Minos technique
// = "B" Use this option when you want to fix one or more parameters
// and the fitting function is like "gaus","expo","poln","landau".
// = "M" More. Improve fit results
// = "R" Use the Range specified in the function range
// = "N" Do not store the graphics function, do not draw
// = "0" Do not plot the result of the fit. By default the fitted function
// is drawn unless the option"N" above is specified.
// = "+" Add this new fitted function to the list of fitted functions
// (by default, any previous function is deleted)
// = "C" In case of linear fitting, don't calculate the chisquare
// (saves time)
// = "F" If fitting a polN, switch to minuit fitter
//
// When the fit is drawn (by default), the parameter goption may be used
// to specify a list of graphics options. See TH1::Draw for a complete
// list of these options.
//
// In order to use the Range option, one must first create a function
// with the expression to be fitted. For example, if your histogram
// has a defined range between -4 and 4 and you want to fit a gaussian
// only in the interval 1 to 3, you can do:
// TF1 *f1 = new TF1("f1","gaus",1,3);
// histo->Fit("f1","R");
//
// Setting initial conditions
// ==========================
// Parameters must be initialized before invoking the Fit function.
// The setting of the parameter initial values is automatic for the
// predefined functions : poln, expo, gaus, landau. One can however disable
// this automatic computation by specifying the option "B".
// Note that if a predefined function is defined with an argument,
// eg, gaus(0), expo(1), you must specify the initial values for
// the parameters.
// You can specify boundary limits for some or all parameters via
// f1->SetParLimits(p_number, parmin, parmax);
// if parmin>=parmax, the parameter is fixed
// Note that you are not forced to fix the limits for all parameters.
// For example, if you fit a function with 6 parameters, you can do:
// func->SetParameters(0,3.1,1.e-6,-8,0,100);
// func->SetParLimits(3,-10,-4);
// func->FixParameter(4,0);
// func->SetParLimits(5, 1,1);
// With this setup, parameters 0->2 can vary freely
// Parameter 3 has boundaries [-10,-4] with initial value -8
// Parameter 4 is fixed to 0
// Parameter 5 is fixed to 100.
// When the lower limit and upper limit are equal, the parameter is fixed.
// However to fix a parameter to 0, one must call the FixParameter function.
//
// Note that option "I" gives better results but is slower.
//
//
// Changing the fitting function
// =============================
// By default the fitting function H1FitChisquare is used.
// To specify a User defined fitting function, specify option "U" and
// call the following functions:
// TVirtualFitter::Fitter(myhist)->SetFCN(MyFittingFunction)
// where MyFittingFunction is of type:
// extern void MyFittingFunction(Int_t &npar, Double_t *gin, Double_t &f, Double_t *u, Int_t flag);
//
// Associated functions
// ====================
// One or more object (typically a TF1*) can be added to the list
// of functions (fFunctions) associated to each histogram.
// When TH1::Fit is invoked, the fitted function is added to this list.
// Given an histogram h, one can retrieve an associated function
// with: TF1 *myfunc = h->GetFunction("myfunc");
//
// Access to the fit results
// =========================
// If the histogram is made persistent, the list of
// associated functions is also persistent. Given a pointer (see above)
// to an associated function myfunc, one can retrieve the function/fit
// parameters with calls such as:
// Double_t chi2 = myfunc->GetChisquare();
// Double_t par0 = myfunc->GetParameter(0); //value of 1st parameter
// Double_t err0 = myfunc->GetParError(0); //error on first parameter
//
// Access to the fit covariance matrix
// ===================================
// Example1:
// TH1F h("h","test",100,-2,2);
// h.FillRandom("gaus",1000);
// h.Fit("gaus");
// Double_t matrix[3][3];
// gMinuit->mnemat(&matrix[0][0],3);
// Example2:
// TH1F h("h","test",100,-2,2);
// h.FillRandom("gaus",1000);
// h.Fit("gaus");
// TVirtualFitter *fitter = TVirtualFitter::GetFitter();
// TMatrixD matrix(npar,npar,fitter->GetCovarianceMatrix());
// Double_t errorFirstPar = fitter->GetCovarianceMatrixElement(0,0);
//
//
// Changing the maximum number of parameters
// =========================================
// By default, the fitter TMinuit is initialized with a maximum of 25 parameters.
// You can redefine this default value by calling :
// TVirtualFitter::Fitter(0,150); //to get a maximum of 150 parameters
//
// Excluding points
// ================
// Use TF1::RejectPoint inside your fitting function to exclude points
// within a certain range from the fit. Example:
// Double_t fline(Double_t *x, Double_t *par)
// {
// if (x[0] > 2.5 && x[0] < 3.5) {
// TF1::RejectPoint();
// return 0;
// }
// return par[0] + par[1]*x[0];
// }
//
// void exclude() {
// TF1 *f1 = new TF1("f1","[0] +[1]*x +gaus(2)",0,5);
// f1->SetParameters(6,-1,5,3,0.2);
// TH1F *h = new TH1F("h","background + signal",100,0,5);
// h->FillRandom("f1",2000);
// TF1 *fline = new TF1("fline",fline,0,5,2);
// fline->SetParameters(2,-1);
// h->Fit("fline","l");
// }
//
// Warning when using the option "0"
// =================================
// When selecting the option "0", the fitted function is added to
// the list of functions of the histogram, but it is not drawn.
// You can undo what you disabled in the following way:
// h.Fit("myFunction","0"); // fit, store function but do not draw
// h.Draw(); function is not drawn
// const Int_t kNotDraw = 1<<9;
// h.GetFunction("myFunction")->ResetBit(kNotDraw);
// h.Draw(); // function is visible again
//
// Access to the Fitter information during fitting
// ===============================================
// This function calls only the abstract fitter TVirtualFitter.
// The default fitter is TFitter (calls TMinuit).
// The default fitter can be set in the resource file in etc/system.rootrc
// Root.Fitter: Fumili
// A different fitter can also be set via TVirtualFitter::SetDefaultFitter.
// For example, to call the "Fumili" fitter instead of "Minuit", do
// TVirtualFitter::SetDefaultFitter("Fumili");
// During the fitting process, the objective function:
// chisquare, likelihood or any user defined algorithm
// is called (see eg in the TFitter class, the static functions
// H1FitChisquare, H1FitLikelihood).
// This objective function, in turn, calls the user theoretical function.
// This user function is a static function called from the TF1 *f1 function.
// Inside this user defined theoretical function , one can access:
// TVirtualFitter *fitter = TVirtualFitter::GetFitter(); //the current fitter
// TH1 *hist = (TH1*)fitter->GetObjectFit(); //the histogram being fitted
// TF1 +f1 = (TF1*)fitter->GetUserFunction(); //the user theoretical function
//
// By default, the fitter TMinuit is initialized with a maximum of 25 parameters.
// For fitting linear functions (containing the "++" sign" and polN functions,
// the linear fitter is initialized.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t fitResult = 0;
Int_t i, npar,nvpar,nparx;
Double_t par, we, al, bl;
Double_t eplus,eminus,eparab,globcc,amin,aminref,edm,errdef,werr;
Double_t params[100], arglist[100];
Axis_t xmin, xmax, ymin, ymax, zmin, zmax, binwidx, binwidy, binwidz;
Int_t hxfirst, hxlast, hyfirst, hylast, hzfirst, hzlast;
TF1 *fnew1;
TF2 *fnew2;
TF3 *fnew3;
// Check validity of function
if (!f1) {
Error("Fit", "function may not be null pointer");
return 0;
}
if (f1->IsZombie()) {
Error("Fit", "function is zombie");
return 0;
}
npar = f1->GetNpar();
if (npar <= 0) {
Error("Fit", "function %s has illegal number of parameters = %d", f1->GetName(), npar);
return 0;
}
// Check that function has same dimension as histogram
if (f1->GetNdim() != GetDimension()) {
Error("Fit","function %s dimension, %d, does not match histogram dimension, %d",
f1->GetName(), f1->GetNdim(), GetDimension());
return 0;
}
hxfirst = fXaxis.GetFirst();
hxlast = fXaxis.GetLast();
binwidx = fXaxis.GetBinWidth(hxlast);
xmin = fXaxis.GetBinLowEdge(hxfirst);
xmax = fXaxis.GetBinLowEdge(hxlast) +binwidx;
hyfirst = fYaxis.GetFirst();
hylast = fYaxis.GetLast();
binwidy = fYaxis.GetBinWidth(hylast);
ymin = fYaxis.GetBinLowEdge(hyfirst);
ymax = fYaxis.GetBinLowEdge(hylast) +binwidy;
hzfirst = fZaxis.GetFirst();
hzlast = fZaxis.GetLast();
binwidz = fZaxis.GetBinWidth(hzlast);
zmin = fZaxis.GetBinLowEdge(hzfirst);
zmax = fZaxis.GetBinLowEdge(hzlast) +binwidz;
// - Decode list of options into fitOption
Foption_t fitOption;
if (!FitOptionsMake(option,fitOption)) return 0;
if (xxmin != xxmax) {
f1->SetRange(xxmin,ymin,zmin,xxmax,ymax,zmax);
fitOption.Range = 1;
}
// - Check if Minuit is initialized and create special functions
Int_t special = f1->GetNumber();
Bool_t linear = f1->IsLinear();
if (special==299+npar)
linear = kTRUE;
if (fitOption.Bound || fitOption.Like || fitOption.Errors || fitOption.Gradient || fitOption.More || fitOption.User|| fitOption.Integral || fitOption.Minuit)
linear = kFALSE;
char l[] ="TLinearFitter";
Int_t strdiff = 0;
Bool_t isSet = kFALSE;
if (TVirtualFitter::GetFitter()){
//Is a fitter already set? Is it linear?
isSet=kTRUE;
strdiff = strcmp(TVirtualFitter::GetFitter()->IsA()->GetName(), l);
}
if (linear){
//
TClass *cl = gROOT->GetClass("TLinearFitter");
if (isSet && strdiff!=0) {
delete TVirtualFitter::GetFitter();
isSet=kFALSE;
}
if (!isSet) {
TVirtualFitter::SetFitter((TVirtualFitter *)cl->New());
}
} else {
if (isSet && strdiff==0){
delete TVirtualFitter::GetFitter();
isSet=kFALSE;
}
if (!isSet)
TVirtualFitter::SetFitter(0);
}
TVirtualFitter *hFitter = TVirtualFitter::Fitter(this, f1->GetNpar());
hFitter->Clear();
// - Get pointer to the function by searching in the list of functions in ROOT
gF1 = f1;
hFitter->SetUserFunc(f1);
if (xxmin != xxmax) f1->SetRange(xxmin,ymin,zmin,xxmax,ymax,zmax);
hFitter->SetFitOption(fitOption);
// - Is a Fit range specified?
Double_t fxmin, fymin, fzmin, fxmax, fymax, fzmax;
if (fitOption.Range) {
f1->GetRange(fxmin, fymin, fzmin, fxmax, fymax, fzmax);
if (fxmin > xmin) xmin = fxmin;
if (fymin > ymin) ymin = fymin;
if (fzmin > zmin) zmin = fzmin;
if (fxmax < xmax) xmax = fxmax;
if (fymax < ymax) ymax = fymax;
if (fzmax < zmax) zmax = fzmax;
hxfirst = fXaxis.FindFixBin(xmin); if (hxfirst < 1) hxfirst = 1;
hxlast = fXaxis.FindFixBin(xmax); if (hxlast > fXaxis.GetLast()) hxlast = fXaxis.GetLast();
hyfirst = fYaxis.FindFixBin(ymin); if (hyfirst < 1) hyfirst = 1;
hylast = fYaxis.FindFixBin(ymax); if (hylast > fYaxis.GetLast()) hylast = fYaxis.GetLast();
hzfirst = fZaxis.FindFixBin(zmin); if (hzfirst < 1) hzfirst = 1;
hzlast = fZaxis.FindFixBin(zmax); if (hzlast > fZaxis.GetLast()) hzlast = fZaxis.GetLast();
} else {
f1->SetRange(xmin,ymin,zmin,xmax,ymax,zmax);
}
hFitter->SetXfirst(hxfirst); hFitter->SetXlast(hxlast);
hFitter->SetYfirst(hyfirst); hFitter->SetYlast(hylast);
hFitter->SetZfirst(hzfirst); hFitter->SetZlast(hzlast);
if (linear){
hFitter->ExecuteCommand("FitHist", 0, 0);
} else {
// - If case of a predefined function, then compute initial values of parameters
if (fitOption.Bound) special = 0;
if (special == 100) H1InitGaus();
else if (special == 400) H1InitGaus();
else if (special == 200) H1InitExpo();
else if (special == 299+npar) H1InitPolynom();
// - Some initialisations
if (!fitOption.Verbose) {
arglist[0] = -1;
hFitter->ExecuteCommand("SET PRINT", arglist,1);
arglist[0] = 0;
hFitter->ExecuteCommand("SET NOW", arglist,0);
}
// - Set error criterion for chisquare or likelihood methods
// - MINUIT ErrDEF should not be set to 0.5 in case of loglikelihood fit.
// - because the FCN is already multiplied by 2 in H1FitLikelihood
// - if Hoption.User is specified, assume that the user has already set
// - his minimization function via SetFCN.
arglist[0] = TVirtualFitter::GetErrorDef();
if (fitOption.Like) {
hFitter->SetFitMethod("H1FitLikelihood");
} else {
if (!fitOption.User) hFitter->SetFitMethod("H1FitChisquare");
}
hFitter->ExecuteCommand("SET Err",arglist,1);
// - Transfer names and initial values of parameters to Minuit
Int_t nfixed = 0;
for (i=0;i<npar;i++) {
par = f1->GetParameter(i);
f1->GetParLimits(i,al,bl);
if (al*bl != 0 && al >= bl) {
al = bl = 0;
arglist[nfixed] = i+1;
nfixed++;
}
we = 0.1*TMath::Abs(bl-al);
if (we == 0) we = 0.3*TMath::Abs(par);
if (we == 0) we = binwidx;
hFitter->SetParameter(i,f1->GetParName(i),par,we,al,bl);
}
if(nfixed > 0)hFitter->ExecuteCommand("FIX",arglist,nfixed); // Otto
// - Set Gradient
if (fitOption.Gradient) {
if (fitOption.Gradient == 1) arglist[0] = 1;
else arglist[0] = 0;
hFitter->ExecuteCommand("SET GRAD",arglist,1);
}
// - Reset Print level
if (fitOption.Verbose) {
arglist[0] = 0; hFitter->ExecuteCommand("SET PRINT", arglist,1);
}
// - Compute sum of squares of errors in the bin range
Double_t ey, sumw2=0;
for (i=hxfirst;i<=hxlast;i++) {
ey = GetBinError(i);
sumw2 += ey*ey;
}
//
//
// printf("h1: sumw2=%f\n", sumw2);
//
// - Perform minimization
arglist[0] = TVirtualFitter::GetMaxIterations();
arglist[1] = sumw2*TVirtualFitter::GetPrecision();
fitResult = hFitter->ExecuteCommand("MIGRAD",arglist,2);
if (fitResult != 0) {
// Abnormal termination, MIGRAD might not have converged on a
// minimum.
if (!fitOption.Quiet) {
Warning("Fit","Abnormal termination of minimization.");
}
}
if (fitOption.More) {
hFitter->ExecuteCommand("IMPROVE",arglist,0);
}
if (fitOption.Errors) {
hFitter->ExecuteCommand("HESSE",arglist,0);
hFitter->ExecuteCommand("MINOS",arglist,0);
}
// - Get return status
char parName[50];
for (i=0;i<npar;i++) {
hFitter->GetParameter(i,parName, par,we,al,bl);
if (!fitOption.Errors) werr = we;
else {
hFitter->GetErrors(i,eplus,eminus,eparab,globcc);
if (eplus > 0 && eminus < 0) werr = 0.5*(eplus-eminus);
else werr = we;
}
params[i] = par;
f1->SetParameter(i,par);
f1->SetParError(i,werr);
}
hFitter->GetStats(aminref,edm,errdef,nvpar,nparx);
// If Log Likelihood, compute an equivalent chisquare
//if (fitOption.Like) amin = hFitter->Chisquare(npar, params, amin, params, 1);
amin = aminref;
if (fitOption.Like) amin = hFitter->Chisquare(npar, params);
f1->SetChisquare(amin);
f1->SetNDF(f1->GetNumberFitPoints()-npar+nfixed);
}
// - Print final values of parameters.
if (!fitOption.Quiet) {
if (fitOption.Errors) hFitter->PrintResults(4,aminref);
else hFitter->PrintResults(3,aminref);
}
// - Store fitted function in histogram functions list and draw
if (!fitOption.Nostore) {
if (!fitOption.Plus) {
TIter next(fFunctions, kIterBackward);
TObject *obj;
while ((obj = next())) {
if (obj->InheritsFrom(TF1::Class())) {
fFunctions->Remove(obj);
delete obj;
}
}
}
if (GetDimension() < 2) {
fnew1 = new TF1();
f1->Copy(*fnew1);
fFunctions->Add(fnew1);
fnew1->SetParent(this);
fnew1->Save(xmin,xmax,0,0,0,0);
if (fitOption.Nograph) fnew1->SetBit(TF1::kNotDraw);
fnew1->SetBit(TFormula::kNotGlobal);
} else if (GetDimension() < 3) {
fnew2 = new TF2();
f1->Copy(*fnew2);
fFunctions->Add(fnew2);
fnew2->SetParent(this);
fnew2->Save(xmin,xmax,ymin,ymax,0,0);
if (fitOption.Nograph) fnew2->SetBit(TF1::kNotDraw);
fnew2->SetBit(TFormula::kNotGlobal);
} else {
fnew3 = new TF3();
f1->Copy(*fnew3);
fFunctions->Add(fnew3);
fnew3->SetParent(this);
fnew3->SetBit(TFormula::kNotGlobal);
}
if (TestBit(kCanDelete)) return fitResult;
if (!fitOption.Nograph && GetDimension() < 3) Draw(goption);
}
return fitResult;
}
//______________________________________________________________________________
void TH1::FitPanel()
{
// -*-*-*-*-*Display a panel with all histogram fit options*-*-*-*-*-*
// ==============================================
//
// See class TFitPanel for example
if (fPainter) fPainter->FitPanel();
}
//______________________________________________________________________________
TH1 *TH1::GetAsymmetry(TH1* h2, Double_t c2, Double_t dc2)
{
// return an histogram containing the asymmetry of this histogram with h2,
// where the asymmetry is defined as:
//
// Asymmetry = (h1 - h2)/(h1 + h2) where h1 = this
//
// works for 1D, 2D, etc. histograms
// c2 is an optional argument that gives a relative weight between the two
// histograms, and dc2 is the error on this weight. This is useful, for example,
// when forming an asymmetry between two histograms from 2 different data sets that
// need to be normalized to each other in some way. The function calculates
// the errors asumming Poisson statistics on h1 and h2 (that is, dh = sqrt(h)).
//
// example: assuming 'h1' and 'h2' are already filled
//
// h3 = h1->GetAsymmetry(h2)
//
// then 'h3' is created and filled with the asymmetry between 'h1' and 'h2';
// h1 and h2 are left intact.
//
// Note that it is the user's responsibility to manage the created histogram.
//
// code proposed by Jason Seely (seely@mit.edu) and adapted by R.Brun
//
// clone the histograms so top and bottom will have the
// correct dimensions:
// Sumw2 just makes sure the errors will be computed properly
// when we form sums and ratios below.
Bool_t addStatus = TH1::AddDirectoryStatus();
TH1::AddDirectory(kFALSE);
TH1 *asym = (TH1*)Clone();
asym->Sumw2();
TH1 *top = (TH1*)asym->Clone();
TH1 *bottom = (TH1*)asym->Clone();
TH1::AddDirectory(addStatus);
// form the top and bottom of the asymmetry, and then divide:
TH1 *h1 = this;
top->Add(h1,h2,1,-c2);
bottom->Add(h1,h2,1,c2);
asym->Divide(top,bottom);
Int_t xmax = asym->GetNbinsX();
Int_t ymax = asym->GetNbinsY();
Int_t zmax = asym->GetNbinsZ();
Double_t bot, error, a, b, da, db;
// now loop over bins to calculate the correct errors
// the reason this error calculation looks complex is because of c2
for(Int_t i=1; i<= xmax; i++){
for(Int_t j=1; j<= ymax; j++){
for(Int_t k=1; k<= zmax; k++){
// here some bin contents are written into variables to make the error
// calculation a little more legible:
a = h1->GetBinContent(i,j,k);
b = h2->GetBinContent(i,j,k);
bot = bottom->GetBinContent(i,j,k);
// make sure there are some events, if not, then the errors are set = 0
// automatically.
if(bot < 1){}
else{
// computation of errors by Christos Leonidopoulos
da = h1->GetBinError(i,j,k);
db = h2->GetBinError(i,j,k);
error = 2*TMath::Sqrt(a*a*c2*c2*db*db + c2*c2*b*b*da*da+a*a*b*b*dc2*dc2)/(bot*bot);
asym->SetBinError(i,j,k,error);
}
}
}
}
delete top;
delete bottom;
return asym;
}
//______________________________________________________________________________
Int_t TH1::GetDefaultBufferSize()
{
// return the default buffer size for automatic histograms
// the parameter fgBufferSize may be changed via SetDefaultBufferSize
return fgBufferSize;
}
//______________________________________________________________________________
Double_t TH1::GetEntries() const
{
// return the current number of entries
if (fBuffer) ((TH1*)this)->BufferEmpty();
return fEntries;
}
//______________________________________________________________________________
char *TH1::GetObjectInfo(Int_t px, Int_t py) const
{
// Redefines TObject::GetObjectInfo.
// Displays the histogram info (bin number, contents, integral up to bin
// corresponding to cursor position px,py
//
return ((TH1*)this)->GetPainter()->GetObjectInfo(px,py);
}
//______________________________________________________________________________
TVirtualHistPainter *TH1::GetPainter()
{
// return pointer to painter
// if painter does not exist, it is created
if (!fPainter) fPainter = TVirtualHistPainter::HistPainter(this);
return fPainter;
}
//______________________________________________________________________________
Int_t TH1::GetQuantiles(Int_t nprobSum, Double_t *q, const Double_t *probSum)
{
// Compute Quantiles for this histogram
// Quantile x_q of a probability distribution Function F is defined as
//
// F(x_q) = q with 0 <= q <= 1.
//
// For instance the median x_0.5 of a distribution is defined as that value
// of the random variable for which the distribution function equals 0.5:
//
// F(x_0.5) = Probability(x < x_0.5) = 0.5
//
// code from Eddy Offermann, Renaissance
//
// input parameters
// - this 1-d histogram (TH1F,D,etc). Could also be a TProfile
// - nprobSum maximum size of array q and size of array probSum (if given)
// - probSum array of positions where quantiles will be computed.
// if probSum is null, probSum will be computed internally and will
// have a size = number of bins + 1 in h. it will correspond to the
// quantiles calculated at the lowest edge of the histogram (quantile=0) and
// all the upper edges of the bins.
// if probSum is not null, it is assumed to contain at least nprobSum values.
// output
// - return value nq (<=nprobSum) with the number of quantiles computed
// - array q filled with nq quantiles
//
// Note that the Integral of the histogram is automatically recomputed
// if the number of entries is different of the number of entries when
// the integral was computed last time. In case you do not use the Fill
// functions to fill your histogram, but SetBinContent, you must call
// TH1::ComputeIntegral before calling this function.
//
// Getting quantiles q from two histograms and storing results in a TGraph,
// a so-called QQ-plot
//
// TGraph *gr = new TGraph(nprob);
// h1->GetQuantiles(nprob,gr->GetX());
// h2->GetQuantiles(nprob,gr->GetY());
// gr->Draw("alp");
//
// Example:
// void quantiles() {
// // demo for quantiles
// const Int_t nq = 20;
// TH1F *h = new TH1F("h","demo quantiles",100,-3,3);
// h->FillRandom("gaus",5000);
//
// Double_t xq[nq]; // position where to compute the quantiles in [0,1]
// Double_t yq[nq]; // array to contain the quantiles
// for (Int_t i=0;i<nq;i++) xq[i] = Float_t(i+1)/nq;
// h->GetQuantiles(nq,yq,xq);
//
// //show the original histogram in the top pad
// TCanvas *c1 = new TCanvas("c1","demo quantiles",10,10,700,900);
// c1->Divide(1,2);
// c1->cd(1);
// h->Draw();
//
// // show the quantiles in the bottom pad
// c1->cd(2);
// gPad->SetGrid();
// TGraph *gr = new TGraph(nq,xq,yq);
// gr->SetMarkerStyle(21);
// gr->Draw("alp");
// }
if (GetDimension() > 1) {
Error("GetQuantiles","Only available for 1-d histograms");
return 0;
}
const Int_t nbins = GetXaxis()->GetNbins();
if (!fIntegral) ComputeIntegral();
if (fIntegral && fIntegral[nbins+1] != fEntries) ComputeIntegral();
Int_t i, ibin;
Double_t *prob = (Double_t*)probSum;
Int_t nq = nprobSum;
if (probSum == 0) {
nq = nbins+1;
prob = new Double_t[nq];
prob[0] = 0;
for (i=1;i<nq;i++) {
prob[i] = fIntegral[i]/fIntegral[nbins];
}
}
for (i = 0; i < nq; i++) {
ibin = TMath::BinarySearch(nbins,fIntegral,prob[i]);
while (ibin < nbins-1 && fIntegral[ibin+1] == prob[i]) {
if (fIntegral[ibin+2] == prob[i]) ibin++;
else break;
}
q[i] = GetBinLowEdge(ibin+1);
const Double_t dint = fIntegral[ibin+1]-fIntegral[ibin];
if (dint > 0) q[i] += GetBinWidth(ibin+1)*(prob[i]-fIntegral[ibin])/dint;
}
if (!probSum) delete [] prob;
return nq;
}
//______________________________________________________________________________
Int_t TH1::FitOptionsMake(Option_t *choptin, Foption_t &fitOption)
{
// -*-*-*-*-*-*-*Decode string choptin and fill fitOption structure*-*-*-*-*-*
// ================================================
Int_t nch = strlen(choptin);
if (!nch) return 1;
char chopt[32];
strcpy(chopt,choptin);
for (Int_t i=0;i<nch;i++) chopt[i] = toupper(choptin[i]);
if (strstr(chopt,"Q")) fitOption.Quiet = 1;
if (strstr(chopt,"V")) {fitOption.Verbose = 1; fitOption.Quiet = 0;}
if (strstr(chopt,"L")) fitOption.Like = 1;
if (strstr(chopt,"LL")) fitOption.Like = 2;
if (strstr(chopt,"W")) fitOption.W1 = 1;
if (strstr(chopt,"E")) fitOption.Errors = 1;
if (strstr(chopt,"M")) fitOption.More = 1;
if (strstr(chopt,"R")) fitOption.Range = 1;
if (strstr(chopt,"G")) fitOption.Gradient= 1;
if (strstr(chopt,"N")) fitOption.Nostore = 1;
if (strstr(chopt,"0")) fitOption.Nograph = 1;
if (strstr(chopt,"+")) fitOption.Plus = 1;
if (strstr(chopt,"I")) fitOption.Integral= 1;
if (strstr(chopt,"B")) fitOption.Bound = 1;
if (strstr(chopt,"U")) {fitOption.User = 1; fitOption.Like = 0;}
if (strstr(chopt,"F")) fitOption.Minuit = 1;
if (strstr(chopt,"C")) fitOption.Nochisq = 1;
return 1;
}
//______________________________________________________________________________
void H1InitGaus()
{
// -*-*-*-*Compute Initial values of parameters for a gaussian*-*-*-*-*-*-*
// ===================================================
Double_t allcha, sumx, sumx2, x, val, rms, mean;
Int_t bin;
const Double_t sqrtpi = 2.506628;
// - Compute mean value and RMS of the histogram in the given range
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
TH1 *curHist = (TH1*)hFitter->GetObjectFit();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
Double_t valmax = curHist->GetBinContent(hxfirst);
Double_t binwidx = curHist->GetBinWidth(hxfirst);
allcha = sumx = sumx2 = 0;
for (bin=hxfirst;bin<=hxlast;bin++) {
x = curHist->GetBinCenter(bin);
val = TMath::Abs(curHist->GetBinContent(bin));
if (val > valmax) valmax = val;
sumx += val*x;
sumx2 += val*x*x;
allcha += val;
}
if (allcha == 0) return;
mean = sumx/allcha;
rms = TMath::Sqrt(sumx2/allcha - mean*mean);
if (rms == 0) rms = binwidx*(hxlast-hxfirst+1)/4;
//if the distribution is really gaussian, the best approximation
//is binwidx*allcha/(sqrtpi*rms)
//However, in case of non-gaussian tails, this underestimates
//the normalisation constant. In this case the maximum value
//is a better approximation.
//We take the average of both quantities
Double_t constant = 0.5*(valmax+binwidx*allcha/(sqrtpi*rms));
//In case the mean value is outside the histo limits and
//the RMS is bigger than the range, we take
// mean = center of bins
// rms = half range
Axis_t xmin = curHist->GetXaxis()->GetXmin();
Axis_t xmax = curHist->GetXaxis()->GetXmax();
if ((mean < xmin || mean > xmax) && rms > (xmax-xmin)) {
mean = 0.5*(xmax+xmin);
rms = 0.5*(xmax-xmin);
}
TF1 *f1 = (TF1*)hFitter->GetUserFunc();
f1->SetParameter(0,constant);
f1->SetParameter(1,mean);
f1->SetParameter(2,rms);
f1->SetParLimits(2,0,10*rms);
}
//______________________________________________________________________________
void H1InitExpo()
{
// -*-*-*-*Compute Initial values of parameters for an exponential*-*-*-*-*
// =======================================================
Double_t constant, slope;
Int_t ifail;
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
Int_t nchanx = hxlast - hxfirst + 1;
H1LeastSquareLinearFit(-nchanx, constant, slope, ifail);
TF1 *f1 = (TF1*)hFitter->GetUserFunc();
f1->SetParameter(0,constant);
f1->SetParameter(1,slope);
}
//______________________________________________________________________________
void H1InitPolynom()
{
// -*-*-*-*Compute Initial values of parameters for a polynom*-*-*-*-*-*-*
// ===================================================
Double_t fitpar[25];
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
TF1 *f1 = (TF1*)hFitter->GetUserFunc();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
Int_t nchanx = hxlast - hxfirst + 1;
Int_t npar = f1->GetNpar();
if (nchanx <=1 || npar == 1) {
TH1 *curHist = (TH1*)hFitter->GetObjectFit();
fitpar[0] = curHist->GetSumOfWeights()/Double_t(nchanx);
} else {
H1LeastSquareFit( nchanx, npar, fitpar);
}
for (Int_t i=0;i<npar;i++) f1->SetParameter(i, fitpar[i]);
}
//______________________________________________________________________________
void H1LeastSquareFit(Int_t n, Int_t m, Double_t *a)
{
// -*-*-*-*-*-*Least squares lpolynomial fitting without weights*-*-*-*-*-*-*
// =================================================
//
// n number of points to fit
// m number of parameters
// a array of parameters
//
// based on CERNLIB routine LSQ: Translated to C++ by Rene Brun
// (E.Keil. revised by B.Schorr, 23.10.1981.)
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
const Double_t zero = 0.;
const Double_t one = 1.;
const Int_t idim = 20;
Double_t b[400] /* was [20][20] */;
Int_t i, k, l, ifail;
Double_t power;
Double_t da[20], xk, yk;
if (m <= 2) {
H1LeastSquareLinearFit(n, a[0], a[1], ifail);
return;
}
if (m > idim || m > n) return;
b[0] = Double_t(n);
da[0] = zero;
for (l = 2; l <= m; ++l) {
b[l-1] = zero;
b[m + l*20 - 21] = zero;
da[l-1] = zero;
}
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
TH1 *curHist = (TH1*)hFitter->GetObjectFit();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
for (k = hxfirst; k <= hxlast; ++k) {
xk = curHist->GetBinCenter(k);
yk = curHist->GetBinContent(k);
power = one;
da[0] += yk;
for (l = 2; l <= m; ++l) {
power *= xk;
b[l-1] += power;
da[l-1] += power*yk;
}
for (l = 2; l <= m; ++l) {
power *= xk;
b[m + l*20 - 21] += power;
}
}
for (i = 3; i <= m; ++i) {
for (k = i; k <= m; ++k) {
b[k - 1 + (i-1)*20 - 21] = b[k + (i-2)*20 - 21];
}
}
H1LeastSquareSeqnd(m, b, idim, ifail, 1, da);
for (i=0; i<m; ++i) a[i] = da[i];
}
//______________________________________________________________________________
void H1LeastSquareLinearFit(Int_t ndata, Double_t &a0, Double_t &a1, Int_t &ifail)
{
// -*-*-*-*-*-*-*-*Least square linear fit without weights*-*-*-*-*-*-*-*-*
// =======================================
//
// extracted from CERNLIB LLSQ: Translated to C++ by Rene Brun
// (added to LSQ by B. Schorr, 15.02.1982.)
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Double_t xbar, ybar, x2bar;
Int_t i, n;
Double_t xybar;
Double_t fn, xk, yk;
Double_t det;
n = TMath::Abs(ndata);
ifail = -2;
xbar = ybar = x2bar = xybar = 0;
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
TH1 *curHist = (TH1*)hFitter->GetObjectFit();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
for (i = hxfirst; i <= hxlast; ++i) {
xk = curHist->GetBinCenter(i);
yk = curHist->GetBinContent(i);
if (ndata < 0) {
if (yk <= 0) yk = 1e-9;
yk = TMath::Log(yk);
}
xbar += xk;
ybar += yk;
x2bar += xk*xk;
xybar += xk*yk;
}
fn = Double_t(n);
det = fn*x2bar - xbar*xbar;
ifail = -1;
if (det <= 0) {
a0 = ybar/fn;
a1 = 0;
return;
}
ifail = 0;
a0 = (x2bar*ybar - xbar*xybar) / det;
a1 = (fn*xybar - xbar*ybar) / det;
}
//______________________________________________________________________________
void H1LeastSquareSeqnd(Int_t n, Double_t *a, Int_t idim, Int_t &ifail, Int_t k, Double_t *b)
{
// -*-*-*-*-*-*Extracted from CERN Program library routine DSEQN*-*-*-*-*-*
// =================================================
//
// : Translated to C++ by Rene Brun
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t a_dim1, a_offset, b_dim1, b_offset;
Int_t nmjp1, i, j, l;
Int_t im1, jp1, nm1, nmi;
Double_t s1, s21, s22;
const Double_t one = 1.;
/* Parameter adjustments */
b_dim1 = idim;
b_offset = b_dim1 + 1;
b -= b_offset;
a_dim1 = idim;
a_offset = a_dim1 + 1;
a -= a_offset;
if (idim < n) return;
ifail = 0;
for (j = 1; j <= n; ++j) {
if (a[j + j*a_dim1] <= 0) { ifail = -1; return; }
a[j + j*a_dim1] = one / a[j + j*a_dim1];
if (j == n) continue;
jp1 = j + 1;
for (l = jp1; l <= n; ++l) {
a[j + l*a_dim1] = a[j + j*a_dim1] * a[l + j*a_dim1];
s1 = -a[l + (j+1)*a_dim1];
for (i = 1; i <= j; ++i) { s1 = a[l + i*a_dim1] * a[i + (j+1)*a_dim1] + s1; }
a[l + (j+1)*a_dim1] = -s1;
}
}
if (k <= 0) return;
for (l = 1; l <= k; ++l) {
b[l*b_dim1 + 1] = a[a_dim1 + 1]*b[l*b_dim1 + 1];
}
if (n == 1) return;
for (l = 1; l <= k; ++l) {
for (i = 2; i <= n; ++i) {
im1 = i - 1;
s21 = -b[i + l*b_dim1];
for (j = 1; j <= im1; ++j) {
s21 = a[i + j*a_dim1]*b[j + l*b_dim1] + s21;
}
b[i + l*b_dim1] = -a[i + i*a_dim1]*s21;
}
nm1 = n - 1;
for (i = 1; i <= nm1; ++i) {
nmi = n - i;
s22 = -b[nmi + l*b_dim1];
for (j = 1; j <= i; ++j) {
nmjp1 = n - j + 1;
s22 = a[nmi + nmjp1*a_dim1]*b[nmjp1 + l*b_dim1] + s22;
}
b[nmi + l*b_dim1] = -s22;
}
}
}
//______________________________________________________________________________
Int_t TH1::GetBin(Int_t binx, Int_t biny, Int_t binz) const
{
// -*-*-*-*Return Global bin number corresponding to binx,y,z*-*-*-*-*-*-*
// ==================================================
//
// 2-D and 3-D histograms are represented with a one dimensional
// structure.
// This has the advantage that all existing functions, such as
// GetBinContent, GetBinError, GetBinFunction work for all dimensions.
//
// In case of a TH1x, returns binx directly.
//
// Convention for numbering bins
// =============================
// For all histogram types: nbins, xlow, xup
// bin = 0; underflow bin
// bin = 1; first bin with low-edge xlow INCLUDED
// bin = nbins; last bin with upper-edge xup EXCLUDED
// bin = nbins+1; overflow bin
// In case of 2-D or 3-D histograms, a "global bin" number is defined.
// For example, assuming a 3-D histogram with binx,biny,binz, the function
// Int_t bin = h->GetBin(binx,biny,binz);
// returns a global/linearized bin number. This global bin is useful
// to access the bin information independently of the dimension.
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t nx, ny, nz;
if (GetDimension() < 2) {
nx = fXaxis.GetNbins()+2;
if (binx < 0) binx = 0;
if (binx >= nx) binx = nx-1;
return binx;
}
if (GetDimension() < 3) {
nx = fXaxis.GetNbins()+2;
if (binx < 0) binx = 0;
if (binx >= nx) binx = nx-1;
ny = fYaxis.GetNbins()+2;
if (biny < 0) biny = 0;
if (biny >= ny) biny = ny-1;
return binx + nx*biny;
}
if (GetDimension() < 4) {
nx = fXaxis.GetNbins()+2;
if (binx < 0) binx = 0;
if (binx >= nx) binx = nx-1;
ny = fYaxis.GetNbins()+2;
if (biny < 0) biny = 0;
if (biny >= ny) biny = ny-1;
nz = fZaxis.GetNbins()+2;
if (binz < 0) binz = 0;
if (binz >= nz) binz = nz-1;
return binx + nx*(biny +ny*binz);
}
return -1;
}
//______________________________________________________________________________
Axis_t TH1::GetRandom() const
{
// return a random number distributed according the histogram bin contents.
// This function checks if the bins integral exists. If not, the integral
// is evaluated, normalized to one.
// The integral is automatically recomputed if the number of entries
// is not the same then when the integral was computed.
// NB Only valid for 1-d histograms. Use GetRandom2 or 3 otherwise.
if (fDimension > 1) {
Error("GetRandom","Function only valid for 1-d histograms");
return 0;
}
Int_t nbinsx = GetNbinsX();
Double_t integral;
if (fIntegral) {
if (fIntegral[nbinsx+1] != fEntries) integral = ((TH1*)this)->ComputeIntegral();
} else {
integral = ((TH1*)this)->ComputeIntegral();
if (integral == 0 || fIntegral == 0) return 0;
}
Double_t r1 = gRandom->Rndm();
Int_t ibin = TMath::BinarySearch(nbinsx,fIntegral,r1);
return GetBinLowEdge(ibin+1)
+GetBinWidth(ibin+1)*(r1-fIntegral[ibin])/(fIntegral[ibin+1] - fIntegral[ibin]);
}
//______________________________________________________________________________
Stat_t TH1::GetBinContent(Int_t) const
{
// -*-*-*-*-*Return content of bin number bin
// ================================
// Implemented in TH1C,S,F,D
//
// Convention for numbering bins
// =============================
// For all histogram types: nbins, xlow, xup
// bin = 0; underflow bin
// bin = 1; first bin with low-edge xlow INCLUDED
// bin = nbins; last bin with upper-edge xup EXCLUDED
// bin = nbins+1; overflow bin
// In case of 2-D or 3-D histograms, a "global bin" number is defined.
// For example, assuming a 3-D histogram with binx,biny,binz, the function
// Int_t bin = h->GetBin(binx,biny,binz);
// returns a global/linearized bin number. This global bin is useful
// to access the bin information independently of the dimension.
AbstractMethod("GetBinContent");
return 0;
}
//______________________________________________________________________________
Stat_t TH1::GetBinContent(Int_t binx, Int_t biny) const
{
// -*-*-*-*-*Return content of bin number binx, biny
// =======================================
// NB: Function to be called for 2-d histograms only
// see convention for numbering bins in TH1::GetBin
Int_t bin = GetBin(binx,biny);
return GetBinContent(bin);
}
//______________________________________________________________________________
Stat_t TH1::GetBinContent(Int_t binx, Int_t biny, Int_t binz) const
{
// -*-*-*-*-*Return content of bin number binx,biny,binz
// ===========================================
// NB: Function to be called for 3-d histograms only
// see convention for numbering bins in TH1::GetBin
Int_t bin = GetBin(binx,biny,binz);
return GetBinContent(bin);
}
//______________________________________________________________________________
TAxis *TH1::GetXaxis() const
{
// return a pointer to the X axis object
return &((TH1*)this)->fXaxis;
}
//______________________________________________________________________________
TAxis *TH1::GetYaxis() const
{
// return a pointer to the Y axis object
return &((TH1*)this)->fYaxis;
}
//______________________________________________________________________________
TAxis *TH1::GetZaxis() const
{
// return a pointer to the Z axis object
return &((TH1*)this)->fZaxis;
}
//___________________________________________________________________________
void TH1::LabelsDeflate(Option_t *ax)
{
// Reduce the number of bins for this axis to the number of bins having a label.
Int_t iaxis = AxisChoice(ax);
TAxis *axis = 0;
if (iaxis == 1) axis = GetXaxis();
if (iaxis == 2) axis = GetYaxis();
if (iaxis == 3) axis = GetZaxis();
if (!axis) return;
if (!axis->GetLabels()) return;
TIter next(axis->GetLabels());
TObject *obj;
Int_t nbins = 0;
while ((obj = next())) {
if (obj->GetUniqueID()) nbins++;
}
if (nbins < 1) nbins = 1;
TH1 *hold = (TH1*)Clone();
hold->SetDirectory(0);
Bool_t timedisp = axis->GetTimeDisplay();
Double_t xmin = axis->GetXmin();
Double_t xmax = axis->GetBinUpEdge(nbins);
if (xmax <= xmin) xmax = xmin +nbins;
axis->SetRange(0,0);
axis->Set(nbins,xmin,xmax);
//Int_t nbinsx = fXaxis.GetNbins();
//Int_t nbinsy = fYaxis.GetNbins();
//Int_t nbinsz = fZaxis.GetNbins();
Int_t nbinsx = hold->GetXaxis()->GetNbins();
Int_t nbinsy = hold->GetYaxis()->GetNbins();
Int_t nbinsz = hold->GetZaxis()->GetNbins();
Int_t ncells = nbinsx+2;
if (GetDimension() > 1) ncells *= nbinsy+2;
if (GetDimension() > 2) ncells *= nbinsz+2;
SetBinsLength(ncells);
Int_t errors = fSumw2.fN;
if (errors) fSumw2.Set(ncells);
axis->SetTimeDisplay(timedisp);
//now loop on all bins and refill
Double_t err,cu;
Int_t bin,ibin,binx,biny,binz;
Double_t oldEntries = fEntries;
for (binz=1;binz<=nbinsz;binz++) {
for (biny=1;biny<=nbinsy;biny++) {
for (binx=1;binx<=nbinsx;binx++) {
bin = hold->GetBin(binx,biny,binz);
ibin= GetBin(binx,biny,binz);
cu = hold->GetBinContent(bin);
SetBinContent(ibin,cu);
if (errors) {
err = hold->GetBinError(bin);
SetBinError(ibin,err);
}
}
}
}
fEntries = oldEntries;
delete hold;
}
//______________________________________________________________________________
void TH1::LabelsInflate(Option_t *ax)
{
// Double the number of bins for axis.
// Refill histogram
// This function is called by TAxis::FindBin(const char *label)
Int_t iaxis = AxisChoice(ax);
TAxis *axis = 0;
if (iaxis == 1) axis = GetXaxis();
if (iaxis == 2) axis = GetYaxis();
if (iaxis == 3) axis = GetZaxis();
if (!axis) return;
TH1 *hold = (TH1*)Clone();
hold->SetDirectory(0);
Bool_t timedisp = axis->GetTimeDisplay();
Int_t nbxold = fXaxis.GetNbins();
Int_t nbyold = fYaxis.GetNbins();
Int_t nbzold = fZaxis.GetNbins();
Int_t nbins = axis->GetNbins();
Double_t xmin = axis->GetXmin();
Double_t xmax = axis->GetXmax();
xmax = xmin + 2*(xmax-xmin);
axis->SetRange(0,0);
axis->Set(2*nbins,xmin,xmax);
Int_t nbinsx = fXaxis.GetNbins();
Int_t nbinsy = fYaxis.GetNbins();
Int_t nbinsz = fZaxis.GetNbins();
Int_t ncells = nbinsx+2;
if (GetDimension() > 1) ncells *= nbinsy+2;
if (GetDimension() > 2) ncells *= nbinsz+2;
SetBinsLength(ncells);
Int_t errors = fSumw2.fN;
if (errors) fSumw2.Set(ncells);
axis->SetTimeDisplay(timedisp);
//now loop on all bins and refill
Double_t err,cu;
Int_t bin,ibin,binx,biny,binz;
for (binz=1;binz<=nbinsz;binz++) {
for (biny=1;biny<=nbinsy;biny++) {
for (binx=1;binx<=nbinsx;binx++) {
bin = hold->GetBin(binx,biny,binz);
ibin= GetBin(binx,biny,binz);
if (binx > nbxold || biny > nbyold || binz > nbzold) bin = -1;
if (bin > 0) cu = hold->GetBinContent(bin);
else cu = 0;
SetBinContent(ibin,cu);
if (errors) {
if (bin > 0) err = hold->GetBinError(bin);
else err = 0;
SetBinError(ibin,err);
}
}
}
}
delete hold;
}
//______________________________________________________________________________
void TH1::LabelsOption(Option_t *option, Option_t *ax)
{
// Set option(s) to draw axis with labels
// option = "a" sort by alphabetic order
// = ">" sort by decreasing values
// = "<" sort by increasing values
// = "h" draw labels horizonthal
// = "v" draw labels vertical
// = "u" draw labels up (end of label right adjusted)
// = "d" draw labels down (start of label left adjusted)
Int_t iaxis = AxisChoice(ax);
TAxis *axis = 0;
if (iaxis == 1) axis = GetXaxis();
if (iaxis == 2) axis = GetYaxis();
if (iaxis == 3) axis = GetZaxis();
if (!axis) return;
THashList *labels = axis->GetLabels();
if (!labels) {
Warning("LabelsOption","Cannot sort. No labels");
return;
}
TString opt = option;
opt.ToLower();
if (opt.Contains("h")) {
axis->SetBit(TAxis::kLabelsHori);
axis->ResetBit(TAxis::kLabelsVert);
axis->ResetBit(TAxis::kLabelsDown);
axis->ResetBit(TAxis::kLabelsUp);
}
if (opt.Contains("v")) {
axis->SetBit(TAxis::kLabelsVert);
axis->ResetBit(TAxis::kLabelsHori);
axis->ResetBit(TAxis::kLabelsDown);
axis->ResetBit(TAxis::kLabelsUp);
}
if (opt.Contains("u")) {
axis->SetBit(TAxis::kLabelsUp);
axis->ResetBit(TAxis::kLabelsVert);
axis->ResetBit(TAxis::kLabelsDown);
axis->ResetBit(TAxis::kLabelsHori);
}
if (opt.Contains("d")) {
axis->SetBit(TAxis::kLabelsDown);
axis->ResetBit(TAxis::kLabelsVert);
axis->ResetBit(TAxis::kLabelsHori);
axis->ResetBit(TAxis::kLabelsUp);
}
Int_t sort = -1;
if (opt.Contains("a")) sort = 0;
if (opt.Contains(">")) sort = 1;
if (opt.Contains("<")) sort = 2;
if (sort < 0) return;
if (sort > 0 && GetDimension() > 2) {
Error("LabelsOption","Sorting by value not implemented for 3-D histograms");
return;
}
Int_t n = TMath::Min(axis->GetNbins(), labels->GetSize());
Int_t *a = new Int_t[n+2];
Int_t i,j,k;
Double_t *cont = 0;
Double_t *errors = 0;
THashList *labold = new THashList(labels->GetSize(),1);
TIter nextold(labels);
TObject *obj;
while ((obj=nextold())) {
labold->Add(obj);
}
labels->Clear();
if (sort > 0) {
//---sort by values of bins
if (GetDimension() == 1) {
cont = new Double_t[n];
if (fSumw2.fN) errors = new Double_t[n];
for (i=1;i<=n;i++) {
cont[i-1] = GetBinContent(i);
if (errors) errors[i-1] = GetBinError(i);
}
if (sort ==1) TMath::Sort(n,cont,a,kTRUE); //sort by decreasing values
else TMath::Sort(n,cont,a,kFALSE); //sort by increasing values
for (i=1;i<=n;i++) {
SetBinContent(i,cont[a[i-1]]);
if (errors) SetBinError(i,errors[a[i-1]]);
}
for (i=1;i<=n;i++) {
obj = labold->At(a[i-1]);
labels->Add(obj);
obj->SetUniqueID(i);
}
} else if (GetDimension()== 2) {
Double_t *pcont = new Double_t[n+2];
for (i=0;i<=n;i++) pcont[i] = 0;
Int_t nx = fXaxis.GetNbins();
Int_t ny = fYaxis.GetNbins();
cont = new Double_t[(nx+2)*(ny+2)];
if (fSumw2.fN) errors = new Double_t[n];
for (i=1;i<=nx;i++) {
for (j=1;j<=ny;j++) {
cont[i+nx*j] = GetBinContent(i,j);
if (errors) errors[i+nx*j] = GetBinError(i,j);
if (axis == GetXaxis()) k = i;
else k = j;
pcont[k-1] += cont[i+nx*j];
}
}
if (sort ==1) TMath::Sort(n,pcont,a,kTRUE); //sort by decreasing values
else TMath::Sort(n,pcont,a,kFALSE); //sort by increasing values
for (i=0;i<n;i++) {
obj = labold->At(a[i]);
labels->Add(obj);
obj->SetUniqueID(i+1);
}
delete [] pcont;
for (i=1;i<=nx;i++) {
for (j=1;j<=ny;j++) {
if (axis == GetXaxis()) {
SetBinContent(i,j,cont[a[i-1]+1+nx*j]);
if (errors) SetBinError(i,j,errors[a[i-1]+1+nx*j]);
} else {
SetBinContent(i,j,cont[i+nx*(a[j-1]+1)]);
if (errors) SetBinError(i,j,errors[i+nx*(a[j-1]+1)]);
}
}
}
} else {
//to be implemented
}
} else {
//---alphabetic sort
const UInt_t kUsed = 1<<18;
TObject *objk=0;
a[0] = 0;
a[n+1] = n+1;
for (i=1;i<=n;i++) {
const char *label = "zzzzzzzzzzzz";
for (j=1;j<=n;j++) {
obj = labold->At(j-1);
if (!obj) continue;
if (obj->TestBit(kUsed)) continue;
//use strcasecmp for case non-sensitive sort (may be an option)
if (strcmp(label,obj->GetName()) < 0) continue;
objk = obj;
a[i] = j;
label = obj->GetName();
}
if (objk) {
objk->SetUniqueID(i);
labels->Add(objk);
objk->SetBit(kUsed);
}
}
for (i=1;i<=n;i++) {
obj = labels->At(i-1);
if (!obj) continue;
obj->ResetBit(kUsed);
}
if (GetDimension() == 1) {
cont = new Double_t[n+2];
if (fSumw2.fN) errors = new Double_t[n+2];
for (i=1;i<=n;i++) {
cont[i] = GetBinContent(a[i]);
if (errors) errors[i] = GetBinError(a[i]);
}
for (i=1;i<=n;i++) {
SetBinContent(i,cont[i]);
if (errors) SetBinError(i,errors[i]);
}
} else if (GetDimension()== 2) {
Int_t nx = fXaxis.GetNbins()+2;
Int_t ny = fYaxis.GetNbins()+2;
cont = new Double_t[nx*ny];
if (fSumw2.fN) errors = new Double_t[nx*ny];
for (i=0;i<nx;i++) {
for (j=0;j<ny;j++) {
cont[i+nx*j] = GetBinContent(i,j);
if (errors) errors[i+nx*j] = GetBinError(i,j);
}
}
for (i=0;i<nx;i++) {
for (j=0;j<ny;j++) {
if (axis == GetXaxis()) {
SetBinContent(i,j,cont[a[i]+nx*j]);
if (errors) SetBinError(i,j,errors[a[i]+nx*j]);
} else {
SetBinContent(i,j,cont[i+nx*a[j]]);
if (errors) SetBinError(i,j,errors[i+nx*a[j]]);
}
}
}
} else {
Int_t nx = fXaxis.GetNbins()+2;
Int_t ny = fYaxis.GetNbins()+2;
Int_t nz = fZaxis.GetNbins()+2;
cont = new Double_t[nx*ny*nz];
if (fSumw2.fN) errors = new Double_t[nx*ny*nz];
for (i=0;i<nx;i++) {
for (j=0;j<ny;j++) {
for (k=0;k<nz;k++) {
cont[i+nx*(j+ny*k)] = GetBinContent(i,j,k);
if (errors) errors[i+nx*(j+ny*k)] = GetBinError(i,j,k);
}
}
}
for (i=0;i<nx;i++) {
for (j=0;j<ny;j++) {
for (k=0;k<nz;k++) {
if (axis == GetXaxis()) {
SetBinContent(i,j,k,cont[a[i]+nx*(j+ny*k)]);
if (errors) SetBinError(i,j,k,errors[a[i]+nx*(j+ny*k)]);
} else if (axis == GetYaxis()) {
SetBinContent(i,j,k,cont[i+nx*(a[j]+ny*k)]);
if (errors) SetBinError(i,j,k,errors[i+nx*(a[j]+ny*k)]);
} else {
SetBinContent(i,j,k,cont[i+nx*(j+ny*a[k])]);
if (errors) SetBinError(i,j,k,errors[i+nx*(j+ny*a[k])]);
}
}
}
}
}
}
delete labold;
if (a) delete [] a;
if (cont) delete [] cont;
if (errors) delete [] errors;
}
//______________________________________________________________________________
static Bool_t AlmostEqual(Double_t a, Double_t b, Double_t epsilon = 0.00000001)
{
return TMath::Abs(a - b) < epsilon;
}
//______________________________________________________________________________
static Bool_t AlmostInteger(Double_t a, Double_t epsilon = 0.00000001)
{
return AlmostEqual(a - TMath::Floor(a), 0, epsilon) ||
AlmostEqual(a - TMath::Floor(a), 1, epsilon);
}
//______________________________________________________________________________
Bool_t TH1::SameLimitsAndNBins(const TAxis& axis1, const TAxis& axis2)
{
if ((axis1.GetNbins() == axis2.GetNbins())
&& (axis1.GetXmin() == axis2.GetXmin())
&& (axis1.GetXmax() == axis2.GetXmax()))
return kTRUE;
else
return kFALSE;
}
//______________________________________________________________________________
Bool_t TH1::RecomputeAxisLimits(TAxis& destAxis, const TAxis& anAxis)
{
// Finds new limits for the axis for the Merge function.
// returns false if the limits are incompatible
if (SameLimitsAndNBins(destAxis, anAxis))
return kTRUE;
if (destAxis.GetXbins()->fN || anAxis.GetXbins()->fN)
return kFALSE; // user binning not supported
Axis_t width1 = destAxis.GetBinWidth(0);
Axis_t width2 = anAxis.GetBinWidth(0);
if (width1 == 0 || width2 == 0)
return kFALSE; // no binning not supported
Axis_t xmin = TMath::Min(destAxis.GetXmin(), anAxis.GetXmin());
Axis_t xmax = TMath::Max(destAxis.GetXmax(), anAxis.GetXmax());
Axis_t width = TMath::Max(width1, width2);
// check the bin size
if (!AlmostInteger(width/width1) || !AlmostInteger(width/width2))
return kFALSE;
// check the limits
Axis_t delta;
delta = (destAxis.GetXmin() - xmin)/width1;
if (!AlmostInteger(delta))
xmin -= (TMath::Ceil(delta) - delta)*width1;
delta = (anAxis.GetXmin() - xmin)/width2;
if (!AlmostInteger(delta))
xmin -= (TMath::Ceil(delta) - delta)*width2;
delta = (destAxis.GetXmin() - xmin)/width1;
if (!AlmostInteger(delta))
return kFALSE;
delta = (xmax - destAxis.GetXmax())/width1;
if (!AlmostInteger(delta))
xmax += (TMath::Ceil(delta) - delta)*width1;
delta = (xmax - anAxis.GetXmax())/width2;
if (!AlmostInteger(delta))
xmax += (TMath::Ceil(delta) - delta)*width2;
delta = (xmax - destAxis.GetXmax())/width1;
if (!AlmostInteger(delta))
return kFALSE;
#ifdef DEBUG
if (!AlmostInteger((xmax - xmin) / width)) { // unnecessary check
printf("TH1::RecomputeAxisLimits - Impossible\n");
return kFALSE;
}
#endif
destAxis.Set(TMath::Nint((xmax - xmin)/width), xmin, xmax);
return kTRUE;
}
//______________________________________________________________________________
Long64_t TH1::Merge(TCollection *li)
{
// Add all histograms in the collection to this histogram.
// This function computes the min/max for the x axis,
// compute a new number of bins, if necessary,
// add bin contents, errors and statistics.
// If all histograms have bin labels, bins with identical labels
// will be merged, no matter what their order is.
// If overflows are present and limits are different the function will fail.
// The function returns the total number of entries in the result histogram
// if the merge is successfull, -1 otherwise.
//
// IMPORTANT remark. The axis x may have different number
// of bins and different limits, BUT the largest bin width must be
// a multiple of the smallest bin width and the upper limit must also
// be a multiple of the bin width.
// Example:
// void atest() {
// TH1F *h1 = new TH1F("h1","h1",110,-110,0);
// TH1F *h2 = new TH1F("h2","h2",220,0,110);
// TH1F *h3 = new TH1F("h3","h3",330,-55,55);
// TRandom r;
// for (Int_t i=0;i<10000;i++) {
// h1->Fill(r.Gaus(-55,10));
// h2->Fill(r.Gaus(55,10));
// h3->Fill(r.Gaus(0,10));
// }
//
// TList *list = new TList;
// list->Add(h1);
// list->Add(h2);
// list->Add(h3);
// TH1F *h = (TH1F*)h1->Clone("h");
// h->Reset();
// h.Merge(list);
// h->Draw();
// }
if (!li) return 0;
if (li->IsEmpty()) return (Int_t) GetEntries();
TList inlist;
TH1* hclone = (TH1*)Clone("FirstClone");
BufferEmpty(1); // To remove buffer.
Reset(); // BufferEmpty sets limits so we can't use it later.
SetEntries(0);
inlist.Add(hclone);
inlist.AddAll(li);
THashList allLabels;
THashList* labels=GetXaxis()->GetLabels();
Bool_t haveOneLabel=kFALSE;
if (labels) {
TIter iL(labels);
TObjString* lb;
while ((lb=(TObjString*)iL())) {
haveOneLabel |= (lb && lb->String().Length());
if (!allLabels.FindObject(lb))
allLabels.Add(lb);
}
}
TAxis newXAxis;
Bool_t initialLimitsFound = kFALSE;
Bool_t allHaveLabels = haveOneLabel;
Bool_t same = kTRUE;
Bool_t allHaveLimits = kTRUE;
TIter next(&inlist);
while (TObject *o = next()) {
TH1* h = dynamic_cast<TH1*> (o);
if (!h) {
Error("Add","Attempt to add object of class: %s to a %s",
o->ClassName(),this->ClassName());
return -1;
}
Bool_t hasLimits = h->GetXaxis()->GetXmin() < h->GetXaxis()->GetXmax();
allHaveLimits = allHaveLimits && hasLimits;
if (hasLimits) {
h->BufferEmpty();
if (!initialLimitsFound) {
initialLimitsFound = kTRUE;
newXAxis.Set(h->GetXaxis()->GetNbins(), h->GetXaxis()->GetXmin(),
h->GetXaxis()->GetXmax());
}
else {
if (!RecomputeAxisLimits(newXAxis, *(h->GetXaxis()))) {
Error("Merge", "Cannot merge histograms - limits are inconsistent:\n "
"first: (%d, %f, %f), second: (%d, %f, %f)",
newXAxis.GetNbins(), newXAxis.GetXmin(), newXAxis.GetXmax(),
h->GetXaxis()->GetNbins(), h->GetXaxis()->GetXmin(),
h->GetXaxis()->GetXmax());
}
}
}
if (allHaveLabels) {
THashList* labels=h->GetXaxis()->GetLabels();
Bool_t haveOneLabel=kFALSE;
if (labels) {
TIter iL(labels);
TObjString* lb;
while ((lb=(TObjString*)iL())) {
haveOneLabel |= (lb && lb->String().Length());
if (!allLabels.FindObject(lb)) {
allLabels.Add(lb);
same = kFALSE;
}
}
}
allHaveLabels&=(labels && haveOneLabel);
if (!allHaveLabels)
Warning("Merge","Not all histograms have labels. I will ignore labels,"
" falling back to bin numbering mode.");
}
}
next.Reset();
same = same && SameLimitsAndNBins(newXAxis, *GetXaxis());
if (!same && initialLimitsFound)
SetBins(newXAxis.GetNbins(), newXAxis.GetXmin(), newXAxis.GetXmax());
if (!allHaveLimits) {
// fill this histogram with all the data from buffers of histograms without limits
while (TH1* h = (TH1*)next()) {
if (h->GetXaxis()->GetXmin() >= h->GetXaxis()->GetXmax() && h->fBuffer) {
// no limits
Int_t nbentries = (Int_t)h->fBuffer[0];
for (Int_t i = 0; i < nbentries; i++)
Fill(h->fBuffer[2*i + 2], h->fBuffer[2*i + 1]);
// Entries from buffers have to be filled one by one
// because FillN doesn't resize histograms.
}
}
if (!initialLimitsFound)
return (Int_t) GetEntries(); // all histograms have been processed
next.Reset();
}
//merge bin contents and errors
Stat_t stats[kNstat], totstats[kNstat];
for (Int_t i=0;i<kNstat;i++) {totstats[i] = stats[i] = 0;}
GetStats(totstats);
Stat_t nentries = GetEntries();
Int_t binx, ix, nx;
Double_t cu;
Bool_t canRebin=TestBit(kCanRebin);
ResetBit(kCanRebin); // reset, otherwise setting the under/overflow will rebin
while (TH1* h=(TH1*)next()) {
// process only if the histogram has limits; otherwise it was processed before
if (h->GetXaxis()->GetXmin() < h->GetXaxis()->GetXmax()) {
// import statistics
h->GetStats(stats);
for (Int_t i=0;i<kNstat;i++)
totstats[i] += stats[i];
nentries += h->GetEntries();
nx = h->GetXaxis()->GetNbins();
for (binx = 0; binx <= nx + 1; binx++) {
cu = h->GetBinContent(binx);
if (!allHaveLabels || !binx || binx==nx+1) {
if ((!same) && (binx == 0 || binx == nx + 1)) {
if (cu != 0) {
Error("Merge", "Cannot merge histograms - the histograms have"
" different limits and undeflows/overflows are present."
" The initial histogram is now broken!");
return -1;
}
}
ix = fXaxis.FindBin(h->GetXaxis()->GetBinCenter(binx));
} else {
const char* label=h->GetXaxis()->GetBinLabel(binx);
if (!label) label="";
ix = fXaxis.FindBin(label);
}
AddBinContent(ix,cu);
if (fSumw2.fN) {
Double_t error1 = h->GetBinError(binx);
fSumw2.fArray[ix] += error1*error1;
}
}
}
}
if (canRebin) SetBit(kCanRebin);
//copy merged stats
PutStats(totstats);
SetEntries(nentries);
if (hclone) delete hclone;
return (Long64_t)nentries;
}
//______________________________________________________________________________
void TH1::Multiply(TF1 *f1, Double_t c1)
{
// Performs the operation: this = this*c1*f1
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
//
// Only bins inside the function range are recomputed.
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Multiply
if (!f1) {
Error("Add","Attempt to multiply by a non-existing function");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// - Add statistics
Double_t nEntries = fEntries;
Stat_t s1[10];
Int_t i;
for (i=0;i<10;i++) {s1[i] = 0;}
PutStats(s1);
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu,w;
Double_t xx[3];
Double_t *params = 0;
f1->InitArgs(xx,params);
for (binz=0;binz<=nbinsz+1;binz++) {
xx[2] = fZaxis.GetBinCenter(binz);
for (biny=0;biny<=nbinsy+1;biny++) {
xx[1] = fYaxis.GetBinCenter(biny);
for (binx=0;binx<=nbinsx+1;binx++) {
xx[0] = fXaxis.GetBinCenter(binx);
if (!f1->IsInside(xx)) continue;
TF1::RejectPoint(kFALSE);
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
Double_t error1 = GetBinError(bin);
cu = c1*f1->EvalPar(xx);
if (TF1::RejectedPoint()) continue;
w = GetBinContent(bin)*cu;
SetBinContent(bin,w);
if (fSumw2.fN) {
fSumw2.fArray[bin] = cu*cu*error1*error1;
}
}
}
}
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Multiply(const TH1 *h1)
{
// -*-*-*-*-*-*-*-*-*Multiply this histogram by h1*-*-*-*-*-*-*-*-*-*-*-*-*
// =============================
//
// this = this*h1
//
// If errors of this are available (TH1::Sumw2), errors are recalculated.
// Note that if h1 has Sumw2 set, Sumw2 is automatically called for this
// if not already set.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Multiply
if (!h1) {
Error("Multiply","Attempt to multiply by a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()) {
Error("Multiply","Attempt to multiply histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Multiply","Attempt to multiply histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 has Sumw2 set
if (fSumw2.fN == 0 && h1->GetSumw2N() != 0) Sumw2();
// - Reset statistics
Double_t nEntries = fEntries;
fEntries = fTsumw = 0;
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t c0,c1,w;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = GetBin(binx,biny,binz);
c0 = GetBinContent(bin);
c1 = h1->GetBinContent(bin);
w = c0*c1;
SetBinContent(bin,w);
fEntries++;
if (fSumw2.fN) {
Double_t e0 = GetBinError(bin);
Double_t e1 = h1->GetBinError(bin);
fSumw2.fArray[bin] = (e0*e0*c1*c1 + e1*e1*c0*c0);
}
}
}
}
Stat_t s[kNstat];
GetStats(s);
PutStats(s);
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Multiply(const TH1 *h1, const TH1 *h2, Double_t c1, Double_t c2, Option_t *option)
{
// -*-*-*Replace contents of this histogram by multiplication of h1 by h2*-*
// ================================================================
//
// this = (c1*h1)*(c2*h2)
//
// If errors of this are available (TH1::Sumw2), errors are recalculated.
// Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this
// if not already set.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Multiply
TString opt = option;
opt.ToLower();
// Bool_t binomial = kFALSE;
// if (opt.Contains("b")) binomial = kTRUE;
if (!h1 || !h2) {
Error("Multiply","Attempt to multiply by a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()
|| nbinsx != h2->GetNbinsX() || nbinsy != h2->GetNbinsY() || nbinsz != h2->GetNbinsZ()) {
Error("Multiply","Attempt to multiply histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Multiply","Attempt to multiply histograms with different axis limits");
}
if (fXaxis.GetXmin() != h2->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h2->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h2->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h2->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h2->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h2->fZaxis.GetXmax()) {
Warning("Multiply","Attempt to multiply histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 or h2 have Sumw2 set
if (fSumw2.fN == 0 && (h1->GetSumw2N() != 0 || h2->GetSumw2N() != 0)) Sumw2();
// - Reset statistics
Double_t nEntries = fEntries;
fEntries = fTsumw = fTsumw2 = fTsumwx = fTsumwx2 = 0;
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t b1,b2,w,d1,d2;
d1 = c1*c1;
d2 = c2*c2;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
b1 = h1->GetBinContent(bin);
b2 = h2->GetBinContent(bin);
w = (c1*b1)*(c2*b2);
SetBinContent(bin,w);
fEntries++;
if (fSumw2.fN) {
Double_t e1 = h1->GetBinError(bin);
Double_t e2 = h2->GetBinError(bin);
fSumw2.fArray[bin] = d1*d2*(e1*e1*b2*b2 + e2*e2*b1*b1);
}
}
}
}
Stat_t s[kNstat];
GetStats(s);
PutStats(s);
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Paint(Option_t *option)
{
// -*-*-*-*-*-*-*Control routine to paint any kind of histograms*-*-*-*-*-*-*
// ===============================================
//
// This function is automatically called by TCanvas::Update.
// (see TH1::Draw for the list of options)
GetPainter();
if (fPainter) {
if (strlen(option) > 0) fPainter->Paint(option);
else fPainter->Paint(fOption.Data());
}
}
//______________________________________________________________________________
TH1 *TH1::Rebin(Int_t ngroup, const char*newname)
{
// -*-*-*Rebin this histogram grouping ngroup bins together*-*-*-*-*-*-*-*-*
// ==================================================
// if newname is not blank a new temporary histogram hnew is created.
// else the current histogram is modified (default)
// The parameter ngroup indicates how many bins of this have to me merged
// into one bin of hnew
// If the original histogram has errors stored (via Sumw2), the resulting
// histograms has new errors correctly calculated.
//
// examples: if h1 is an existing TH1F histogram with 100 bins
// h1->Rebin(); //merges two bins in one in h1: previous contents of h1 are lost
// h1->Rebin(5); //merges five bins in one in h1
// TH1F *hnew = h1->Rebin(5,"hnew"); // creates a new histogram hnew
// //merging 5 bins of h1 in one bin
//
// NOTE: If ngroup is not an exact divider of the number of bins,
// the top limit of the rebinned histogram is changed
// to the upper edge of the bin=newbins*ngroup and the corresponding
// bins are added to the overflow bin.
// Statistics will be recomputed from the new bin contents.
Int_t nbins = fXaxis.GetNbins();
Axis_t xmin = fXaxis.GetXmin();
Axis_t xmax = fXaxis.GetXmax();
if ((ngroup <= 0) || (ngroup > nbins)) {
Error("Rebin", "Illegal value of ngroup=%d",ngroup);
return 0;
}
if (fDimension > 1 || InheritsFrom("TProfile")) {
Error("Rebin", "Operation valid on 1-D histograms only");
return 0;
}
Int_t newbins = nbins/ngroup;
// Save old bin contents into a new array
Double_t entries = fEntries;
Double_t *oldBins = new Double_t[nbins];
Int_t bin, i;
for (bin=0;bin<nbins;bin++) oldBins[bin] = GetBinContent(bin+1);
Double_t *oldErrors = 0;
if (fSumw2.fN != 0) {
oldErrors = new Double_t[nbins];
for (bin=0;bin<nbins;bin++) oldErrors[bin] = GetBinError(bin+1);
}
// create a clone of the old histogram if newname is specified
TH1 *hnew = this;
if (newname && strlen(newname) > 0) {
hnew = (TH1*)Clone();
hnew->SetName(newname);
}
// change axis specs and rebuild bin contents array::RebinAx
if(newbins*ngroup != nbins) {
xmax = fXaxis.GetBinUpEdge(newbins*ngroup);
hnew->fTsumw = 0; //stats must be reset because top bins will be moved to overflow bin
}
// save the TAttAxis members (reset by SetBins)
Int_t nDivisions = fXaxis.GetNdivisions();
Color_t axisColor = fXaxis.GetAxisColor();
Color_t labelColor = fXaxis.GetLabelColor();
Style_t labelFont = fXaxis.GetLabelFont();
Float_t labelOffset = fXaxis.GetLabelOffset();
Float_t labelSize = fXaxis.GetLabelSize();
Float_t tickLength = fXaxis.GetTickLength();
Float_t titleOffset = fXaxis.GetTitleOffset();
Float_t titleSize = fXaxis.GetTitleSize();
Color_t titleColor = fXaxis.GetTitleColor();
Style_t titleFont = fXaxis.GetTitleFont();
if(fXaxis.GetXbins()->GetSize() > 0){ // variable bin sizes
Axis_t *bins = new Axis_t[newbins+1];
for(Int_t i = 0; i <= newbins; ++i) bins[i] = fXaxis.GetBinLowEdge(1+i*ngroup);
hnew->SetBins(newbins,bins); //this also changes errors array (if any)
delete [] bins;
} else {
hnew->SetBins(newbins,xmin,xmax); //this also changes errors array (if any)
}
// Restore axis attributes
fXaxis.SetNdivisions(nDivisions);
fXaxis.SetAxisColor(axisColor);
fXaxis.SetLabelColor(labelColor);
fXaxis.SetLabelFont(labelFont);
fXaxis.SetLabelOffset(labelOffset);
fXaxis.SetLabelSize(labelSize);
fXaxis.SetTickLength(tickLength);
fXaxis.SetTitleOffset(titleOffset);
fXaxis.SetTitleSize(titleSize);
fXaxis.SetTitleColor(titleColor);
fXaxis.SetTitleFont(titleFont);
// copy merged bin contents (ignore under/overflows)
Int_t oldbin = 0;
Double_t binContent, binError;
for (bin = 0;bin<=newbins;bin++) {
binContent = 0;
binError = 0;
for (i=0;i<ngroup;i++) {
if (oldbin+i >= nbins) break;
binContent += oldBins[oldbin+i];
if (oldErrors) binError += oldErrors[oldbin+i]*oldErrors[oldbin+i];
}
hnew->SetBinContent(bin+1,binContent);
if (oldErrors) hnew->SetBinError(bin+1,TMath::Sqrt(binError));
oldbin += ngroup;
}
hnew->SetEntries(entries); //was modified by SetBinContent
delete [] oldBins;
if (oldErrors) delete [] oldErrors;
return hnew;
}
//______________________________________________________________________________
Bool_t TH1::FindNewAxisLimits(const TAxis* axis, const Axis_t point, Axis_t& newMin, Axis_t &newMax)
{
// finds new limits for the axis so that *point* is within the range and
// the limits are compatible with the previous ones (see TH1::Merge).
// new limits are put into *newMin* and *newMax* variables.
// axis - axis whose limits are to be recomputed
// point - point that should fit within the new axis limits
// newMin - new minimum will be stored here
// newMax - new maximum will be stored here.
// false if failed (e.g. if the initial axis limits are wrong
// or the new range is more than 2^64 times the old one).
Axis_t xmin = axis->GetXmin();
Axis_t xmax = axis->GetXmax();
if (xmin >= xmax) return kFALSE;
Axis_t range = xmax-xmin;
Axis_t binsize = range / axis->GetNbins();
//recompute new axis limits by doubling the current range
Int_t ntimes = 0;
while (point < xmin) {
if (ntimes++ > 64)
return kFALSE;
xmin = xmin - range;
range *= 2;
binsize *= 2;
// make sure that the merging will be correct
if ( xmin / binsize - TMath::Floor(xmin / binsize) >= 0.5) {
xmin += 0.5 * binsize;
xmax += 0.5 * binsize; // won't work with a histogram with only one bin, but I don't care
}
}
while (point >= xmax) {
if (ntimes++ > 64)
return kFALSE;
xmax = xmax + range;
range *= 2;
binsize *= 2;
// make sure that the merging will be correct
if ( xmin / binsize - TMath::Floor(xmin / binsize) >= 0.5) {
xmin -= 0.5 * binsize;
xmax -= 0.5 * binsize; // won't work with a histogram with only one bin, but I don't care
}
}
newMin = xmin;
newMax = xmax;
// Info("FindNewAxisLimits", "OldAxis: (%lf, %lf), new: (%lf, %lf), point: %lf",
// axis->GetXmin(), axis->GetXmax(), xmin, xmax, point);
return kTRUE;
}
//______________________________________________________________________________
void TH1::RebinAxis(Axis_t x, const char *ax)
{
// Histogram is resized along ax such that x is in the axis range.
// The new axis limits are recomputed by doubling iteratively
// the current axis range until the specified value x is within the limits.
// The algorithm makes a copy of the histogram, then loops on all bins
// of the old histogram to fill the rebinned histogram.
// Takes into account errors (Sumw2) if any.
// The algorithm works for 1-d, 2-d and 3-d histograms.
// The bit kCanRebin must be set before invoking this function.
// Ex: h->SetBit(TH1::kCanRebin);
if (!TestBit(kCanRebin)) return;
if (TMath::IsNaN(x)) { // x may be a NaN
ResetBit(kCanRebin);
return;
}
char achoice = toupper(ax[0]);
TAxis *axis = &fXaxis;
if (achoice == 'Y') axis = &fYaxis;
if (achoice == 'Z') axis = &fZaxis;
if (axis->GetXmin() >= axis->GetXmax()) return;
if (axis->GetNbins() <= 0) return;
Axis_t xmin, xmax;
if (!FindNewAxisLimits(axis, x, xmin, xmax))
return;
//save a copy of this histogram
TH1 *hold = (TH1*)Clone();
hold->SetDirectory(0);
//set new axis limits
axis->SetLimits(xmin,xmax);
Int_t nbinsx = fXaxis.GetNbins();
Int_t nbinsy = fYaxis.GetNbins();
Int_t nbinsz = fZaxis.GetNbins();
//now loop on all bins and refill
Double_t err,cu;
Axis_t bx,by,bz;
Int_t errors = GetSumw2N();
Int_t ix,iy,iz,ibin,binx,biny,binz,bin;
Reset("ICE"); //reset only Integral, contents and Errors
for (binz=1;binz<=nbinsz;binz++) {
bz = hold->GetZaxis()->GetBinCenter(binz);
iz = fZaxis.FindFixBin(bz);
for (biny=1;biny<=nbinsy;biny++) {
by = hold->GetYaxis()->GetBinCenter(biny);
iy = fYaxis.FindFixBin(by);
for (binx=1;binx<=nbinsx;binx++) {
bx = hold->GetXaxis()->GetBinCenter(binx);
ix = fXaxis.FindFixBin(bx);
bin = hold->GetBin(binx,biny,binz);
ibin= GetBin(ix,iy,iz);
cu = hold->GetBinContent(bin);
AddBinContent(ibin,cu);
if (errors) {
err = hold->GetBinError(bin);
fSumw2.fArray[ibin] += err*err;
}
}
}
}
delete hold;
}
//______________________________________________________________________________
void TH1::RecursiveRemove(TObject *obj)
{
// Recursively remove object from the list of functions
if (fFunctions) {
if (!fFunctions->TestBit(kInvalidObject)) fFunctions->RecursiveRemove(obj);
}
}
//______________________________________________________________________________
void TH1::Scale(Double_t c1)
{
// -*-*-*Multiply this histogram by a constant c1*-*-*-*-*-*-*-*-*
// ========================================
//
// this = c1*this
//
// Note that both contents and errors(if any) are scaled.
// This function uses the services of TH1::Add
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Scale
Double_t ent = fEntries;
Add(this,this,c1,0);
fEntries = ent;
//if contours set, must also scale contours
Int_t ncontours = GetContour();
if (ncontours == 0) return;
Double_t *levels = fContour.GetArray();
for (Int_t i=0;i<ncontours;i++) {
levels[i] *= c1;
}
}
//______________________________________________________________________________
void TH1::SetDefaultBufferSize(Int_t buffersize)
{
// static function to set the default buffer size for automatic histograms.
// When an histogram is created with one of its axis lower limit greater
// or equal to its upper limit, the function SetBuffer is automatically
// called with the default buffer size.
if (buffersize < 0) buffersize = 0;
fgBufferSize = buffersize;
}
//______________________________________________________________________________
void TH1::SetTitle(const char *title)
{
// Change (i.e. set) the title
// if title is of the form "stringt;stringx;stringy;stringz"
// the histogram title is set to stringt,
// the x axis title to stringx, the y axis title to stringy,etc
fTitle = title;
// Decode fTitle. It may contain X, Y and Z titles
TString str1 = fTitle, str2;
Int_t isc = str1.Index(";");
Int_t lns = str1.Length();
if (isc >=0 ) {
fTitle = str1(0,isc);
str1 = str1(isc+1, lns);
isc = str1.Index(";");
if (isc >=0 ) {
str2 = str1(0,isc);
fXaxis.SetTitle(str2.Data());
lns = str1.Length();
str1 = str1(isc+1, lns);
isc = str1.Index(";");
if (isc >=0 ) {
str2 = str1(0,isc);
fYaxis.SetTitle(str2.Data());
lns = str1.Length();
str1 = str1(isc+1, lns);
fZaxis.SetTitle(str1.Data());
} else {
fYaxis.SetTitle(str1.Data());
}
} else {
fXaxis.SetTitle(str1.Data());
}
}
if (gPad && TestBit(kMustCleanup)) gPad->Modified();
}
// -------------------------------------------------------------------------
void TH1::SmoothArray(Int_t nn, Double_t *xx, Int_t ntimes)
{
// smooth array xx, translation of Hbook routine hsmoof.F
// based on algorithm 353QH twice presented by J. Friedman
// in Proc.of the 1974 CERN School of Computing, Norway, 11-24 August, 1974.
Int_t ii, jj, ik, jk, kk, nn1, nn2;
Double_t hh[6] = {0,0,0,0,0,0};
Double_t *yy = new Double_t[nn];
Double_t *zz = new Double_t[nn];
Double_t *rr = new Double_t[nn];
for (Int_t pass=0;pass<ntimes;pass++) {
// first copy original data into temp array
for (ii = 0; ii < nn; ii++) {
yy[ii] = xx[ii];
}
// do 353 i.e. running median 3, 5, and 3 in a single loop
for (kk = 1; kk <= 3; kk++) {
ik = 0;
if (kk == 2) ik = 1;
nn1 = ik + 2;
nn2 = nn - ik - 1;
// do all elements beside the first and last point for median 3
// and first two and last 2 for median 5
for (ii = nn1; ii <= nn2; ii++) {
for (jj = 0; jj < 3; jj++) {
hh[jj] = yy[ii + jj - 1];
}
zz[ii] = TMath::Median(3 + 2*ik, hh);
}
if (kk == 1) { // first median 3
// first point
hh[0] = 3*yy[1] - 2*yy[2];
hh[1] = yy[0];
hh[2] = yy[2];
zz[0] = TMath::Median(3, hh);
// last point
hh[0] = yy[nn - 2];
hh[1] = yy[nn - 1];
hh[2] = 3*yy[nn - 2] - 2*yy[nn - 3];
zz[nn - 1] = TMath::Median(3, hh);
}
if (kk == 2) { // median 5
// first point remains the same
zz[0] = yy[0];
for (ii = 0; ii < 3; ii++) {
hh[ii] = yy[ii];
}
zz[1] = TMath::Median(3, hh);
// last two points
for (ii = 0; ii < 3; ii++) {
hh[ii] = yy[nn +nn2 -1 + ii];
}
zz[nn - 2] = TMath::Median(3, hh);
zz[nn - 1] = yy[nn - 1];
}
}
// quadratic interpolation for flat segments
nn2 = nn2 - 2;
for (ii = nn1; ii <= nn2; ii++) {
if (zz[ii - 1] != zz[ii]) continue;
if (zz[ii] != zz[ii + 1]) continue;
hh[0] = zz[ii - 2] - zz[ii];
hh[1] = zz[ii + 2] - zz[ii];
if (hh[0] * hh[1] < 0) continue;
jk = 0;
if ( TMath::Abs(hh[1]) > TMath::Abs(hh[0]) ) jk = -1;
yy[ii] = -0.5*zz[ii - 2*jk] + zz[ii - jk]/0.75 + zz[ii + 2*jk] /6.;
yy[ii + jk] = 0.5*(zz[ii + 2*jk] - zz[ii - 2*jk]) + zz[ii - jk];
}
// running means
for (ii = 1; ii < nn - 1; ii++) {
rr[ii] = 0.25*yy[ii - 1] + 0.5*yy[ii] + 0.25*yy[ii + 1];
}
rr[0] = yy[0];
rr[nn - 1] = yy[nn - 1];
// now do the same for residuals
for (ii = 0; ii < nn; ii++) {
yy[ii] = xx[ii] - rr[ii];
}
// do 353 i.e. running median 3, 5, and 3 in a single loop
for (kk = 1; kk <= 3; kk++) {
ik = 0;
if (kk == 2) ik = 1;
nn1 = ik + 1;
nn2 = nn - ik - 1;
// do all elements beside the first and last point for median 3
// and first two and last 2 for median 5
for (ii = nn1; ii <= nn2; ii++) {
for (jj = 0; jj < 3; jj++) {
hh[jj] = yy[ii + jj - 1];
}
zz[ii] = TMath::Median(3 + 2*ik, hh);
}
if (kk == 1) { // first median 3
// first point
hh[0] = 3*yy[1] - 2*yy[2];
hh[1] = yy[0];
hh[2] = yy[2];
zz[0] = TMath::Median(3, hh);
// last point
hh[0] = yy[nn - 2];
hh[1] = yy[nn - 1];
hh[2] = 3*yy[nn - 2] - 2*yy[nn - 3];
zz[nn - 1] = TMath::Median(3, hh);
}
if (kk == 2) { // median 5
// first point remains the same
zz[0] = yy[0];
for (ii = 0; ii < 3; ii++) {
hh[ii] = yy[ii];
}
zz[1] = TMath::Median(3, hh);
// last two points
for (ii = 0; ii < 3; ii++) {
hh[ii] = yy[nn - 3 + ii];
}
zz[nn - 2] = TMath::Median(3, hh);
zz[nn - 1] = yy[nn - 1];
}
}
// quadratic interpolation for flat segments
nn2 = nn2 - 1;
for (ii = nn1 + 1; ii <= nn2; ii++) {
if (zz[ii - 1] != zz[ii]) continue;
if (zz[ii] != zz[ii + 1]) continue;
hh[0] = zz[ii - 2] - zz[ii];
hh[1] = zz[ii + 2] - zz[ii];
if (hh[0] * hh[1] < 0) continue;
jk = 0;
if ( TMath::Abs(hh[1]) > TMath::Abs(hh[0]) ) jk = -1;
yy[ii] = -0.5*zz[ii - 2*jk] + zz[ii - jk]/0.75 + zz[ii + 2*jk]/6.;
yy[ii + jk] = 0.5*(zz[ii + 2*jk] - zz[ii - 2*jk]) + zz[ii - jk];
}
// running means
for (ii = 1; ii <= nn - 1; ii++) {
zz[ii] = 0.25*yy[ii - 1] + 0.5*yy[ii] + 0.25*yy[ii + 1];
}
zz[0] = yy[0];
zz[nn - 1] = yy[nn - 1];
// add smoothed xx and smoothed residuals
for (ii = 0; ii < nn; ii++) {
if (xx[ii] < 0) xx[ii] = rr[ii] + zz[ii];
else xx[ii] = TMath::Abs(rr[ii] + zz[ii]);
}
}
delete [] yy;
delete [] zz;
delete [] rr;
}
// ------------------------------------------------------------------------
void TH1::Smooth(Int_t ntimes, Int_t firstbin, Int_t lastbin)
{
// Smooth bin contents of this histogram between firstbin and lastbin.
// (if firstbin=-1 and lastbin=-1 (default) all bins are smoothed.
// bin contents are replaced by their smooth values.
// Errors (if any) are not modified.
// algorithm can only be applied to 1-d histograms
if (fDimension != 1) {
Error("Smooth","Smooth only supported for 1-d histograms");
return;
}
Int_t nbins = fXaxis.GetNbins();
if (firstbin < 0) firstbin = 1;
if (lastbin < 0) lastbin = nbins;
if (lastbin > nbins+1) lastbin = nbins;
nbins = lastbin - firstbin + 1;
Double_t *xx = new Double_t[nbins];
Int_t i;
for (i=0;i<nbins;i++) {
xx[i] = GetBinContent(i+firstbin);
}
TH1::SmoothArray(nbins,xx,ntimes);
for (i=0;i<nbins;i++) {
SetBinContent(i+firstbin,xx[i]);
}
delete [] xx;
if (gPad) gPad->Modified();
}
// ------------------------------------------------------------------------
void TH1::StatOverflows(Bool_t flag)
{
// if flag=kTRUE, underflows and overflows are used by the Fill functions
// in the computation of statistics (mean value, RMS).
// By default, underflows or overflows are not used.
fgStatOverflows = flag;
}
//_______________________________________________________________________
void TH1::Streamer(TBuffer &b)
{
// -*-*-*-*-*-*-*Stream a class object*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
// =====================
if (b.IsReading()) {
UInt_t R__s, R__c;
Version_t R__v = b.ReadVersion(&R__s, &R__c);
if (R__v > 2) {
TH1::Class()->ReadBuffer(b, this, R__v, R__s, R__c);
fXaxis.SetParent(this);
fYaxis.SetParent(this);
fZaxis.SetParent(this);
if (fgAddDirectory && !gROOT->ReadingObject()) {
fDirectory = gDirectory;
if (!gDirectory->GetList()->FindObject(this)) gDirectory->Append(this);
}
ResetBit(kCanDelete);
return;
}
//process old versions before automatic schema evolution
TNamed::Streamer(b);
TAttLine::Streamer(b);
TAttFill::Streamer(b);
TAttMarker::Streamer(b);
b >> fNcells;
fXaxis.Streamer(b);
fYaxis.Streamer(b);
fZaxis.Streamer(b);
fXaxis.SetParent(this);
fYaxis.SetParent(this);
fZaxis.SetParent(this);
b >> fBarOffset;
b >> fBarWidth;
b >> fEntries;
b >> fTsumw;
b >> fTsumw2;
b >> fTsumwx;
b >> fTsumwx2;
if (R__v < 2) {
Float_t maximum, minimum, norm;
Float_t *contour=0;
b >> maximum; fMaximum = maximum;
b >> minimum; fMinimum = minimum;
b >> norm; fNormFactor = norm;
Int_t n = b.ReadArray(contour);
fContour.Set(n);
for (Int_t i=0;i<n;i++) fContour.fArray[i] = contour[i];
delete [] contour;
} else {
b >> fMaximum;
b >> fMinimum;
b >> fNormFactor;
fContour.Streamer(b);
}
fSumw2.Streamer(b);
fOption.Streamer(b);
fFunctions->Delete();
fFunctions->Streamer(b);
if (!gROOT->ReadingObject()) {
fDirectory = gDirectory;
if (!gDirectory->GetList()->FindObject(this)) gDirectory->Append(this);
}
b.CheckByteCount(R__s, R__c, TH1::IsA());
} else {
TH1::Class()->WriteBuffer(b,this);
}
}
//______________________________________________________________________________
void TH1::Print(Option_t *option) const
{
// -*-*-*-*-*Print some global quantities for this histogram*-*-*-*-*-*-*-*
// ===============================================
//
// If option "base" is given, number of bins and ranges are also printed
// If option "range" is given, bin contents and errors are also printed
// for all bins in the current range (default 1-->nbins)
// If option "all" is given, bin contents and errors are also printed
// for all bins including under and overflows.
//
printf( "TH1.Print Name = %s, Entries= %d, Total sum= %g\n",GetName(),Int_t(fEntries),GetSumOfWeights());
TString opt = option;
opt.ToLower();
Int_t all;
if (opt.Contains("all")) all = 0;
else if (opt.Contains("range")) all = 1;
else if (opt.Contains("base")) all = 2;
else return;
Int_t bin, binx, biny, binz;
Int_t firstx=0,lastx=0,firsty=0,lasty=0,firstz=0,lastz=0;
if (all == 0) {
lastx = fXaxis.GetNbins()+1;
if (fDimension > 1) lasty = fYaxis.GetNbins()+1;
if (fDimension > 2) lastz = fZaxis.GetNbins()+1;
} else {
firstx = fXaxis.GetFirst(); lastx = fXaxis.GetLast();
if (fDimension > 1) {firsty = fYaxis.GetFirst(); lasty = fYaxis.GetLast();}
if (fDimension > 2) {firstz = fZaxis.GetFirst(); lastz = fZaxis.GetLast();}
}
if (all== 2) {
printf(" Title = %s\n", GetTitle());
printf(" NbinsX= %d, xmin= %g, xmax=%g", fXaxis.GetNbins(), fXaxis.GetXmin(), fXaxis.GetXmax());
if( fDimension > 1) printf(", NbinsY= %d, ymin= %g, ymax=%g", fYaxis.GetNbins(), fYaxis.GetXmin(), fYaxis.GetXmax());
if( fDimension > 2) printf(", NbinsZ= %d, zmin= %g, zmax=%g", fZaxis.GetNbins(), fZaxis.GetXmin(), fZaxis.GetXmax());
printf("\n");
return;
}
Stat_t w,e;
Axis_t x,y,z;
if (fDimension == 1) {
for (binx=firstx;binx<=lastx;binx++) {
x = fXaxis.GetBinCenter(binx);
w = GetBinContent(binx);
e = GetBinError(binx);
if(fSumw2.fN) printf(" fSumw[%d]=%g, x=%g, error=%g\n",binx,w,x,e);
else printf(" fSumw[%d]=%g, x=%g\n",binx,w,x);
}
}
if (fDimension == 2) {
for (biny=firsty;biny<=lasty;biny++) {
y = fYaxis.GetBinCenter(biny);
for (binx=firstx;binx<=lastx;binx++) {
bin = GetBin(binx,biny);
x = fXaxis.GetBinCenter(binx);
w = GetBinContent(bin);
e = GetBinError(bin);
if(fSumw2.fN) printf(" fSumw[%d][%d]=%g, x=%g, y=%g, error=%g\n",binx,biny,w,x,y,e);
else printf(" fSumw[%d][%d]=%g, x=%g, y=%g\n",binx,biny,w,x,y);
}
}
}
if (fDimension == 3) {
for (binz=firstz;binz<=lastz;binz++) {
z = fZaxis.GetBinCenter(binz);
for (biny=firsty;biny<=lasty;biny++) {
y = fYaxis.GetBinCenter(biny);
for (binx=firstx;binx<=lastx;binx++) {
bin = GetBin(binx,biny,binz);
x = fXaxis.GetBinCenter(binx);
w = GetBinContent(bin);
e = GetBinError(bin);
if(fSumw2.fN) printf(" fSumw[%d][%d][%d]=%g, x=%g, y=%g, z=%g, error=%g\n",binx,biny,binz,w,x,y,z,e);
else printf(" fSumw[%d][%d][%d]=%g, x=%g, y=%g, z=%g\n",binx,biny,binz,w,x,y,z);
}
}
}
}
}
//______________________________________________________________________________
void TH1::Rebuild(Option_t *)
{
// Using the current bin info, recompute the arrays for contents and errors
SetBinsLength();
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::Reset(Option_t *option)
{
// -*-*-*-*-*-*Reset this histogram: contents, errors, etc*-*-*-*-*-*-*-*
// ===========================================
//
// if option "ICE" is specified, resets only Integral, Contents and Errors.
TString opt = option;
opt.ToUpper();
fSumw2.Reset();
if (fIntegral) {delete [] fIntegral; fIntegral = 0;}
if (opt.Contains("ICE")) return;
if (fBuffer) BufferEmpty();
fTsumw = 0;
fTsumw2 = 0;
fTsumwx = 0;
fTsumwx2 = 0;
fEntries = 0;
TObject *stats = fFunctions->FindObject("stats");
fFunctions->Remove(stats);
//special logic to support the case where the same object is
//added multiple times in fFunctions.
//This case happens when the same object is added with different
//drawing modes
TObject *obj;
while ((obj = fFunctions->First())) {
while(fFunctions->Remove(obj));
delete obj;
}
if(stats) fFunctions->Add(stats);
fContour.Set(0);
}
//______________________________________________________________________________
void TH1::SavePrimitive(ofstream &out, Option_t *option)
{
// Save primitive as a C++ statement(s) on output stream out
Bool_t nonEqiX = kFALSE;
Bool_t nonEqiY = kFALSE;
Bool_t nonEqiZ = kFALSE;
Int_t i;
// Check if the histogram has equidistant X bins or not. If not, we
// create an array holding the bins.
if (GetXaxis()->GetXbins()->fN && GetXaxis()->GetXbins()->fArray) {
nonEqiX = kTRUE;
out << " Double_t xAxis[" << GetXaxis()->GetXbins()->fN
<< "] = {";
for (i = 0; i < GetXaxis()->GetXbins()->fN; i++) {
if (i != 0) out << ", ";
out << GetXaxis()->GetXbins()->fArray[i];
}
out << "}; " << endl;
}
// If the histogram is 2 or 3 dimensional, check if the histogram
// has equidistant Y bins or not. If not, we create an array
// holding the bins.
if (fDimension > 1 && GetYaxis()->GetXbins()->fN &&
GetYaxis()->GetXbins()->fArray) {
nonEqiY = kTRUE;
out << " Double_t yAxis[" << GetYaxis()->GetXbins()->fN
<< "] = {";
for (i = 0; i < GetYaxis()->GetXbins()->fN; i++) {
if (i != 0) out << ", ";
out << GetYaxis()->GetXbins()->fArray[i];
}
out << "}; " << endl;
}
// IF the histogram is 3 dimensional, check if the histogram
// has equidistant Z bins or not. If not, we create an array
// holding the bins.
if (fDimension > 2 && GetZaxis()->GetXbins()->fN &&
GetZaxis()->GetXbins()->fArray) {
nonEqiZ = kTRUE;
out << " Double_t zAxis[" << GetZaxis()->GetXbins()->fN
<< "] = {";
for (i = 0; i < GetZaxis()->GetXbins()->fN; i++) {
if (i != 0) out << ", ";
out << GetZaxis()->GetXbins()->fArray[i];
}
out << "}; " << endl;
}
char quote = '"';
out <<" "<<endl;
out <<" "<<"TH1"<<" *";
out << GetName() << " = new " << ClassName() << "(" << quote
<< GetName() << quote << "," << quote<< GetTitle() << quote
<< "," << GetXaxis()->GetNbins();
if (nonEqiX)
out << ", xAxis";
else
out << "," << GetXaxis()->GetXmin()
<< "," << GetXaxis()->GetXmax();
if (fDimension > 1) {
out << "," << GetYaxis()->GetNbins();
if (nonEqiY)
out << ", yAxis";
else
out << "," << GetYaxis()->GetXmin()
<< "," << GetYaxis()->GetXmax();
}
if (fDimension > 2) {
out << "," << GetZaxis()->GetNbins();
if (nonEqiZ)
out << ", zAxis";
else
out << "," << GetZaxis()->GetXmin()
<< "," << GetZaxis()->GetXmax();
}
out << ");" << endl;
// save bin contents
Int_t bin;
for (bin=0;bin<fNcells;bin++) {
Double_t bc = GetBinContent(bin);
if (bc) {
out<<" "<<GetName()<<"->SetBinContent("<<bin<<","<<bc<<");"<<endl;
}
}
// save bin errors
if (fSumw2.fN) {
for (bin=0;bin<fNcells;bin++) {
Double_t be = GetBinError(bin);
if (be) {
out<<" "<<GetName()<<"->SetBinError("<<bin<<","<<be<<");"<<endl;
}
}
}
TH1::SavePrimitiveHelp(out, option);
}
//______________________________________________________________________________
void TH1::SavePrimitiveHelp(ofstream &out, Option_t *option)
{
// helper function for the SavePrimitive functions from TH1
// or classes derived from TH1, eg TProfile, TProfile2D.
char quote = '"';
if (TMath::Abs(GetBarOffset()) > 1e-5) {
out<<" "<<GetName()<<"->SetBarOffset("<<GetBarOffset()<<");"<<endl;
}
if (TMath::Abs(GetBarWidth()-1) > 1e-5) {
out<<" "<<GetName()<<"->SetBarWidth("<<GetBarWidth()<<");"<<endl;
}
if (fMinimum != -1111) {
out<<" "<<GetName()<<"->SetMinimum("<<fMinimum<<");"<<endl;
}
if (fMaximum != -1111) {
out<<" "<<GetName()<<"->SetMaximum("<<fMaximum<<");"<<endl;
}
if (fNormFactor != 0) {
out<<" "<<GetName()<<"->SetNormFactor("<<fNormFactor<<");"<<endl;
}
if (fEntries != 0) {
out<<" "<<GetName()<<"->SetEntries("<<fEntries<<");"<<endl;
}
if (fDirectory == 0) {
out<<" "<<GetName()<<"->SetDirectory(0);"<<endl;
}
if (TestBit(kNoStats)) {
out<<" "<<GetName()<<"->SetStats(0);"<<endl;
}
if (fOption.Length() != 0) {
out<<" "<<GetName()<<"->SetOption("<<quote<<fOption.Data()<<quote<<");"<<endl;
}
// save contour levels
Int_t ncontours = GetContour();
if (ncontours > 0) {
out<<" "<<GetName()<<"->SetContour("<<ncontours<<");"<<endl;
for (Int_t bin=0;bin<ncontours;bin++) {
out<<" "<<GetName()<<"->SetContourLevel("<<bin<<","<<GetContourLevel(bin)<<");"<<endl;
}
}
// save list of functions
TObjOptLink *lnk = (TObjOptLink*)fFunctions->FirstLink();
TObject *obj;
while (lnk) {
obj = lnk->GetObject();
obj->SavePrimitive(out,"nodraw");
if (obj->InheritsFrom("TF1")) {
out<<" "<<GetName()<<"->GetListOfFunctions()->Add("<<obj->GetName()<<");"<<endl;
} else if (obj->InheritsFrom("TPaveStats")) {
out<<" "<<GetName()<<"->GetListOfFunctions()->Add(ptstats);"<<endl;
out<<" ptstats->SetParent("<<GetName()<<"->GetListOfFunctions());"<<endl;
} else {
out<<" "<<GetName()<<"->GetListOfFunctions()->Add("<<obj->GetName()<<","<<quote<<lnk->GetOption()<<quote<<");"<<endl;
}
lnk = (TObjOptLink*)lnk->Next();
}
// save attributes
SaveFillAttributes(out,GetName(),0,1001);
SaveLineAttributes(out,GetName(),1,1,1);
SaveMarkerAttributes(out,GetName(),1,1,1);
fXaxis.SaveAttributes(out,GetName(),"->GetXaxis()");
fYaxis.SaveAttributes(out,GetName(),"->GetYaxis()");
fZaxis.SaveAttributes(out,GetName(),"->GetZaxis()");
TString opt = option;
opt.ToLower();
if (!opt.Contains("nodraw")) {
out<<" "<<GetName()<<"->Draw("
<<quote<<option<<quote<<");"<<endl;
}
}
//______________________________________________________________________________
void TH1::UseCurrentStyle()
{
// Copy current attributes from/to current style
if (gStyle->IsReading()) {
fXaxis.ResetAttAxis("X");
fYaxis.ResetAttAxis("Y");
fZaxis.ResetAttAxis("Z");
SetBarOffset(gStyle->GetBarOffset());
SetBarWidth(gStyle->GetBarWidth());
SetFillColor(gStyle->GetHistFillColor());
SetFillStyle(gStyle->GetHistFillStyle());
SetLineColor(gStyle->GetHistLineColor());
SetLineStyle(gStyle->GetHistLineStyle());
SetLineWidth(gStyle->GetHistLineWidth());
SetMarkerColor(gStyle->GetMarkerColor());
SetMarkerStyle(gStyle->GetMarkerStyle());
SetMarkerSize(gStyle->GetMarkerSize());
Int_t dostat = gStyle->GetOptStat();
if (gStyle->GetOptFit() && !dostat) dostat = 1000000001;
SetStats(dostat);
} else {
gStyle->SetBarOffset(fBarOffset);
gStyle->SetBarWidth(fBarWidth);
gStyle->SetHistFillColor(GetFillColor());
gStyle->SetHistFillStyle(GetFillStyle());
gStyle->SetHistLineColor(GetLineColor());
gStyle->SetHistLineStyle(GetLineStyle());
gStyle->SetHistLineWidth(GetLineWidth());
gStyle->SetMarkerColor(GetMarkerColor());
gStyle->SetMarkerStyle(GetMarkerStyle());
gStyle->SetMarkerSize(GetMarkerSize());
gStyle->SetOptStat(TestBit(kNoStats));
}
}
//______________________________________________________________________________
Double_t TH1::GetMean(Int_t axis) const
{
// For axis = 1,2 or 3 returns the mean value of the histogram along
// X,Y or Z axis.
// For axis = 11, 12, 13 returns the standard error of the mean value
// of the histogram along X, Y or Z axis
//
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
// -*-*-*-*-*-*Return mean value of this histogram along the X axis*-*-*-*-*
// ====================================================
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
if (axis<1 || axis>3&&axis<11 || axis>13) return 0;
Stat_t stats[kNstat];
for (Int_t i=4;i<kNstat;i++) stats[i] = 0;
GetStats(stats);
if (stats[0] == 0) return 0;
if (axis<10){
Int_t ax[3] = {2,4,7};
return stats[ax[axis-1]]/stats[0];
} else {
Double_t rms = GetRMS(axis-10);
return (rms/TMath::Sqrt(stats[0]));
}
}
//______________________________________________________________________________
Double_t TH1::GetMeanError(Int_t axis) const
{
// -*-*-*-*-*-*Return standard error of mean of this histogram along the X axis*-*-*-*-*
// ====================================================
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
// Also note, that although the definition of standard error doesn't include the
// assumption of normality, many uses of this feature implicitly assume it.
return GetMean(axis+10);
}
//______________________________________________________________________________
Double_t TH1::GetRMS(Int_t axis) const
{
// For axis = 1,2 or 3 returns the Sigma value of the histogram along
// X, Y or Z axis
// For axis = 11, 12 or 13 returns the error of RMS estimation along
// X, Y or Z axis for Normal distribution
//
// Note that the mean value/sigma is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
// Note that this function returns the Standard Deviation (Sigma)
// of the distribution (not RMS).
// The Sigma estimate is computed as Sqrt((1/N)*(Sum(x_i-x_mean)^2))
// The name "RMS" was introduced many years ago (Hbook/PAW times).
// We kept the name for continuity.
if (axis<1 || axis>3&&axis<11 || axis>13) return 0;
Stat_t x, rms2, stats[kNstat];
for (Int_t i=4;i<kNstat;i++) stats[i] = 0;
GetStats(stats);
if (stats[0] == 0) return 0;
Int_t ax[3] = {2,4,7};
Int_t axm = ax[axis%10 - 1];
x = stats[axm]/stats[0];
rms2 = TMath::Abs(stats[axm+1]/stats[0] -x*x);
if (axis<10)
return TMath::Sqrt(rms2);
else
return TMath::Sqrt(rms2/(2*stats[0]));
}
//______________________________________________________________________________
Double_t TH1::GetRMSError(Int_t axis) const
{
// Return error of RMS estimation for Normal distribution
//
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
// Value returned is standard deviation of sample standard deviation.
return GetRMS(axis+10);
}
//______________________________________________________________________________
Double_t TH1::GetSkewness(Int_t axis) const
{
//For axis = 1, 2 or 3 returns skewness of the histogram along x, y or z axis.
//For axis = 11, 12 or 13 returns the approximate standard error of skewness
//of the histogram along x, y or z axis
//Note, that since third and fourth moment are not calculated
//at the fill time, skewness and its standard error are computed bin by bin
const TAxis *ax;
if (axis==1 || axis==11) ax = &fXaxis;
else if (axis==2 || axis==12) ax = &fYaxis;
else if (axis==3 || axis==13) ax = &fZaxis;
else {
Error("GetSkewness", "illegal value of parameter");
return 0;
}
if (axis < 10) {
//compute skewness
Double_t x, w, mean, rms, rms3, sum=0;
mean = GetMean(axis);
rms = GetRMS(axis);
rms3 = rms*rms*rms;
Int_t bin;
Double_t np=0;
for (bin=ax->GetFirst(); bin<=ax->GetLast(); bin++){
x = GetBinCenter(bin);
w = GetBinContent(bin);
np+=w;
sum+=w*(x-mean)*(x-mean)*(x-mean);
}
sum/=np*rms3;
return sum;
} else {
//compute standard error of skewness
Int_t nbins = ax->GetNbins();
return TMath::Sqrt(6./nbins);
}
}
//______________________________________________________________________________
Double_t TH1::GetKurtosis(Int_t axis) const
{
//For axis =1, 2 or 3 returns kurtosis of the histogram along x, y or z axis.
//Kurtosis(gaussian(0, 1)) = 0.
//For axis =11, 12 or 13 returns the approximate standard error of kurtosis
//of the histogram along x, y or z axis
//Note, that since third and fourth moment are not calculated
//at the fill time, kurtosis and its standard error are computed bin by bin
const TAxis *ax;
if (axis==1 || axis==11) ax = &fXaxis;
else if (axis==2 || axis==12) ax = &fYaxis;
else if (axis==3 || axis==13) ax = &fZaxis;
else {
Error("GetKurtosis", "illegal value of parameter");
return 0;
}
if (axis < 10){
Double_t x, w, mean, rms, rms4, sum=0;
mean = GetMean(axis);
rms = GetRMS(axis);
rms4 = rms*rms*rms*rms;
Int_t bin;
Double_t np=0;
for (bin=ax->GetFirst(); bin<=ax->GetLast(); bin++){
x = GetBinCenter(bin);
w = GetBinContent(bin);
np+=w;
sum+=w*(x-mean)*(x-mean)*(x-mean)*(x-mean);
}
sum/=np*rms4;
return sum-3;
} else {
Int_t nbins = ax->GetNbins();
return TMath::Sqrt(24./nbins);
}
}
//______________________________________________________________________________
void TH1::GetStats(Stat_t *stats) const
{
// fill the array stats from the contents of this histogram
// The array stats must be correctly dimensionned in the calling program.
// stats[0] = sumw
// stats[1] = sumw2
// stats[2] = sumwx
// stats[3] = sumwx2
//
// If no axis-subrange is specified (via TAxis::SetRange), the array stats
// is simply a copy of the statistics quantities computed at filling time.
// If a sub-range is specified, the function recomputes these quantities
// from the bin contents in the current axis range.
//
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
if (fBuffer) ((TH1*)this)->BufferEmpty();
// Loop on bins (possibly including underflows/overflows)
Int_t bin, binx;
Stat_t w,err;
Axis_t x;
if (fTsumw == 0 || fXaxis.TestBit(TAxis::kAxisRange)) {
for (bin=0;bin<4;bin++) stats[bin] = 0;
for (binx=fXaxis.GetFirst();binx<=fXaxis.GetLast();binx++) {
x = fXaxis.GetBinCenter(binx);
w = TMath::Abs(GetBinContent(binx));
err = TMath::Abs(GetBinError(binx));
stats[0] += w;
stats[1] += err*err;
stats[2] += w*x;
stats[3] += w*x*x;
}
} else {
stats[0] = fTsumw;
stats[1] = fTsumw2;
stats[2] = fTsumwx;
stats[3] = fTsumwx2;
}
}
//______________________________________________________________________________
void TH1::PutStats(Stat_t *stats)
{
// Replace current statistics with the values in array stats
fTsumw = stats[0];
fTsumw2 = stats[1];
fTsumwx = stats[2];
fTsumwx2 = stats[3];
}
//______________________________________________________________________________
Stat_t TH1::GetSumOfWeights() const
{
// -*-*-*-*-*-*Return the sum of weights excluding under/overflows*-*-*-*-*
// ===================================================
Int_t bin,binx,biny,binz;
Stat_t sum =0;
for(binz=1; binz<=fZaxis.GetNbins(); binz++) {
for(biny=1; biny<=fYaxis.GetNbins(); biny++) {
for(binx=1; binx<=fXaxis.GetNbins(); binx++) {
bin = GetBin(binx,biny,binz);
sum += GetBinContent(bin);
}
}
}
return sum;
}
//______________________________________________________________________________
Stat_t TH1::Integral(Option_t *option) const
{
//Return integral of bin contents. Only bins in the bins range are considered.
// By default the integral is computed as the sum of bin contents in the range.
// if option "width" is specified, the integral is the sum of
// the bin contents multiplied by the bin width in x.
return Integral(fXaxis.GetFirst(),fXaxis.GetLast(),option);
}
//______________________________________________________________________________
Stat_t TH1::Integral(Int_t binx1, Int_t binx2, Option_t *option) const
{
//Return integral of bin contents between binx1 and binx2 for a 1-D histogram
// By default the integral is computed as the sum of bin contents in the range.
// if option "width" is specified, the integral is the sum of
// the bin contents multiplied by the bin width in x.
if (binx1 < 0) binx1 = 0;
Stat_t integral = 0;
// - Loop on bins in specified range
TString opt = option;
opt.ToLower();
Bool_t width = kFALSE;
if (opt.Contains("width")) width = kTRUE;
Int_t binx;
for (binx=binx1;binx<=binx2;binx++) {
if (width) integral += GetBinContent(binx)*fXaxis.GetBinWidth(binx);
else integral += GetBinContent(binx);
}
return integral;
}
//______________________________________________________________________________
Double_t TH1::KolmogorovTest(const TH1 *h2, Option_t *option) const
{
// Statistical test of compatibility in shape between
// THIS histogram and h2, using Kolmogorov test.
//
// Default: Ignore under- and overflow bins in comparison
//
// option is a character string to specify options
// "U" include Underflows in test (also for 2-dim)
// "O" include Overflows (also valid for 2-dim)
// "N" include comparison of normalizations
// "D" Put out a line of "Debug" printout
// "M" Return the Maximum Kolmogorov distance instead of prob
// "X" Run the pseudo experiments post-processor with the following procedure:
// make pseudoexperiments based on random values from the parent
// distribution and compare the KS distance of the pseudoexperiment
// to the parent distribution. Bin the KS distances in a histogram,
// and then take the integral of all the KS values above the value
// obtained from the original data to Monte Carlo distribution.
// The number of pseudo-experiments nEXPT is currently fixed at 1000.
// The function returns the integral.
// (thanks to Ben Kilminster to submit this procedure). Note that
// this option "X" is much slower.
//
// The returned function value is the probability of test
// (much less than one means NOT compatible)
//
// Code adapted by Rene Brun from original HBOOK routine HDIFF
//
// NOTE1
// A good description of the Kolmogorov test can be seen at:
// http://www.itl.nist.gov/div898/handbook/eda/section3/eda35g.htm
//
// NOTE2
// see also alternative function TH1::Chi2Test
// The Kolmogorov test is assumed to give better results than Chi2Test
// in case of histograms with low statistics.
//
// NOTE3 (Jan Conrad, Fred James)
// "The returned value PROB is calculated such that it will be
// uniformly distributed between zero and one for compatible histograms,
// provided the data are not binned (or the number of bins is very large
// compared with the number of events). Users who have access to unbinned
// data and wish exact confidence levels should therefore not put their data
// into histograms, but should call directly TMath::KolmogorovTest. On
// the other hand, since TH1 is a convenient way of collecting data and
// saving space, this function has been provided. However, the values of
// PROB for binned data will be shifted slightly higher than expected,
// depending on the effects of the binning. For example, when comparing two
// uniform distributions of 500 events in 100 bins, the values of PROB,
// instead of being exactly uniformly distributed between zero and one, have
// a mean value of about 0.56. We can apply a useful
// rule: As long as the bin width is small compared with any significant
// physical effect (for example the experimental resolution) then the binning
// cannot have an important effect. Therefore, we believe that for all
// practical purposes, the probability value PROB is calculated correctly
// provided the user is aware that:
// 1. The value of PROB should not be expected to have exactly the correct
// distribution for binned data.
// 2. The user is responsible for seeing to it that the bin widths are
// small compared with any physical phenomena of interest.
// 3. The effect of binning (if any) is always to make the value of PROB
// slightly too big. That is, setting an acceptance criterion of (PROB>0.05
// will assure that at most 5% of truly compatible histograms are rejected,
// and usually somewhat less."
TString opt = option;
opt.ToUpper();
Double_t prob = 0;
TH1 *h1 = (TH1*)this;
if (h2 == 0) return 0;
TAxis *axis1 = h1->GetXaxis();
TAxis *axis2 = h2->GetXaxis();
Int_t ncx1 = axis1->GetNbins();
Int_t ncx2 = axis2->GetNbins();
// Check consistency of dimensions
if (h1->GetDimension() != 1 || h2->GetDimension() != 1) {
Error("KolmogorovTest","Histograms must be 1-D\n");
return 0;
}
// Check consistency in number of channels
if (ncx1 != ncx2) {
Error("KolmogorovTest","Number of channels is different, %d and %d\n",ncx1,ncx2);
return 0;
}
// Check consistency in channel edges
Double_t difprec = 1e-5;
Double_t diff1 = TMath::Abs(axis1->GetXmin() - axis2->GetXmin());
Double_t diff2 = TMath::Abs(axis1->GetXmax() - axis2->GetXmax());
if (diff1 > difprec || diff2 > difprec) {
Error("KolmogorovTest","histograms with different binning");
return 0;
}
Bool_t afunc1 = kFALSE;
Bool_t afunc2 = kFALSE;
Double_t sum1 = 0, sum2 = 0;
Double_t ew1, ew2, w1 = 0, w2 = 0;
Int_t bin;
for (bin=1;bin<=ncx1;bin++) {
sum1 += h1->GetBinContent(bin);
sum2 += h2->GetBinContent(bin);
ew1 = h1->GetBinError(bin);
ew2 = h2->GetBinError(bin);
w1 += ew1*ew1;
w2 += ew2*ew2;
}
if (sum1 == 0) {
Error("KolmogorovTest","Histogram1 %s integral is zero\n",h1->GetName());
return 0;
}
if (sum2 == 0) {
Error("KolmogorovTest","Histogram2 %s integral is zero\n",h2->GetName());
return 0;
}
Double_t tsum1 = sum1;
Double_t tsum2 = sum2;
if (opt.Contains("U")) {
tsum1 += h1->GetBinContent(0);
tsum2 += h2->GetBinContent(0);
}
if (opt.Contains("O")) {
tsum1 += h1->GetBinContent(ncx1+1);
tsum2 += h2->GetBinContent(ncx1+1);
}
// Check if histograms are weighted.
// If number of entries = number of channels, probably histograms were
// not filled via Fill(), but via SetBinContent()
Double_t ne1 = h1->GetEntries();
Double_t ne2 = h2->GetEntries();
// look at first histogram
Double_t difsum1 = (ne1-tsum1)/tsum1;
Double_t esum1 = sum1;
if (difsum1 > difprec && Int_t(ne1) != ncx1) {
if (opt.Contains("U") || opt.Contains("O")) {
Warning("KolmogorovTest","U/O option with weighted events for hist:%s\n",h1->GetName());
}
if (h1->GetSumw2N() == 0) {
Warning("KolmogorovTest","Weighted events and no Sumw2, hist:%s\n",h1->GetName());
} else {
esum1 = sum1*sum1/w1; //number of equivalent entries
}
}
// look at second histogram
Double_t difsum2 = (ne2-tsum2)/tsum2;
Double_t esum2 = sum2;
if (difsum2 > difprec && Int_t(ne2) != ncx1) {
if (opt.Contains("U") || opt.Contains("O")) {
Warning("KolmogorovTest","U/O option with weighted events for hist:%s\n",h2->GetName());
}
if (h2->GetSumw2N() == 0) {
Warning("KolmogorovTest","Weighted events and no Sumw2, hist:%s\n",h2->GetName());
} else {
esum2 = sum2*sum2/w2; //number of equivalent entries
}
}
Double_t s1 = 1/tsum1;
Double_t s2 = 1/tsum2;
// Find largest difference for Kolmogorov Test
Double_t dfmax =0, rsum1 = 0, rsum2 = 0;
Int_t first = 1;
Int_t last = ncx1;
if (opt.Contains("U")) first = 0;
if (opt.Contains("O")) last = ncx1+1;
for (bin=first;bin<=last;bin++) {
rsum1 += s1*h1->GetBinContent(bin);
rsum2 += s2*h2->GetBinContent(bin);
dfmax = TMath::Max(dfmax,TMath::Abs(rsum1-rsum2));
}
// Get Kolmogorov probability
Double_t z, prb1=0, prb2=0, prb3=0;
if (afunc1) z = dfmax*TMath::Sqrt(esum2);
else if (afunc2) z = dfmax*TMath::Sqrt(esum1);
else z = dfmax*TMath::Sqrt(esum1*esum2/(esum1+esum2));
prob = TMath::KolmogorovProb(z);
if (opt.Contains("N")) {
// Combine probabilities for shape and normalization,
prb1 = prob;
Double_t resum1 = esum1; if (afunc1) resum1 = 0;
Double_t resum2 = esum2; if (afunc2) resum2 = 0;
Double_t d12 = esum1-esum2;
Double_t chi2 = d12*d12/(resum1+resum2);
prb2 = TMath::Prob(chi2,1);
// see Eadie et al., section 11.6.2
if (prob > 0 && prb2 > 0) prob *= prb2*(1-TMath::Log(prob*prb2));
else prob = 0;
}
// X option. Pseudo-experiments post-processor to determine KS probability
const Int_t nEXPT = 1000;
if (opt.Contains("X")) {
Double_t dSEXPT;
Bool_t addStatus = fgAddDirectory;
fgAddDirectory = kFALSE;
TH1F *hDistValues = new TH1F("hDistValues","KS distances",200,0,1);
TH1 *hExpt = (TH1*)Clone();
fgAddDirectory = addStatus;
// make nEXPT experiments (this should be a parameter)
for (Int_t i=0; i < nEXPT; i++) {
hExpt->Reset();
hExpt->FillRandom(h1,(Int_t)ne2);
dSEXPT = KolmogorovTest(hExpt,"M");
hDistValues->Fill(dSEXPT);
}
prb3 = hDistValues->Integral(hDistValues->FindBin(dfmax),200)/hDistValues->Integral();
delete hDistValues;
delete hExpt;
}
// debug printout
if (opt.Contains("D")) {
printf(" Kolmo Prob h1 = %s, sum1=%g\n",h1->GetName(),sum1);
printf(" Kolmo Prob h2 = %s, sum2=%g\n",h2->GetName(),sum2);
printf(" Kolmo Prob = %g, Max Dist = %g\n",prob,dfmax);
if (opt.Contains("N"))
printf(" Kolmo Prob = %f for shape alone, =%f for normalisation alone\n",prb1,prb2);
if (opt.Contains("X"))
printf(" Kolmo Prob = %f with %d pseudo-experiments\n",prb3,nEXPT);
}
// This numerical error condition should never occur:
if (TMath::Abs(rsum1-1) > 0.002) Warning("KolmogorovTest","Numerical problems with h1=%s\n",h1->GetName());
if (TMath::Abs(rsum2-1) > 0.002) Warning("KolmogorovTest","Numerical problems with h2=%s\n",h2->GetName());
if(opt.Contains("M")) return dfmax;
else if(opt.Contains("X")) return prb3;
else return prob;
}
//______________________________________________________________________________
void TH1::SetContent(const Stat_t *content)
{
// -*-*-*-*-*-*Replace bin contents by the contents of array content*-*-*-*
// =====================================================
Int_t bin;
Stat_t bincontent;
for (bin=0; bin<fNcells; bin++) {
bincontent = *(content + bin);
SetBinContent(bin, bincontent);
}
}
//______________________________________________________________________________
Int_t TH1::GetContour(Double_t *levels)
{
// Return contour values into array levels if pointer levels is non zero
//
// The function returns the number of contour levels.
// see GetContourLevel to return one contour only
//
Int_t nlevels = fContour.fN;
if (levels) {
if (nlevels == 0) {
nlevels = 20;
SetContour(nlevels);
} else {
if (TestBit(kUserContour) == 0) SetContour(nlevels);
}
for (Int_t level=0; level<nlevels; level++) levels[level] = fContour.fArray[level];
}
return nlevels;
}
//______________________________________________________________________________
Double_t TH1::GetContourLevel(Int_t level) const
{
// Return value of contour number level
// see GetContour to return the array of all contour levels
if (level <0 || level >= fContour.fN) return 0;
Double_t zlevel = fContour.fArray[level];
return zlevel;
}
//______________________________________________________________________________
Double_t TH1::GetContourLevelPad(Int_t level) const
{
// Return the value of contour number "level" in Pad coordinates ie: if the Pad
// is in log scale along Z it returns le log of the contour level value.
// see GetContour to return the array of all contour levels
if (level <0 || level >= fContour.fN) return 0;
Double_t zlevel = fContour.fArray[level];
// In case of user defined contours and Pad in log scale along Z,
// fContour.fArray doesn't contain the log of the contour whereas it does
// in case of equidistant contours.
if (gPad && gPad->GetLogz() && TestBit(kUserContour)) {
if (zlevel <= 0) return 0;
zlevel = TMath::Log10(zlevel);
}
return zlevel;
}
//______________________________________________________________________________
void TH1::SetBuffer(Int_t buffersize, Option_t * /*option*/)
{
// set the maximum number of entries to be kept in the buffer
if (fBuffer) {
BufferEmpty();
delete [] fBuffer;
fBuffer = 0;
}
if (buffersize <= 0) {
fBufferSize = 0;
return;
}
if (buffersize < 100) buffersize = 100;
fBufferSize = 1 + buffersize*(fDimension+1);
fBuffer = new Double_t[fBufferSize];
memset(fBuffer,0,8*fBufferSize);
}
//______________________________________________________________________________
void TH1::SetContour(Int_t nlevels, const Double_t *levels)
{
// -*-*-*-*-*-*Set the number and values of contour levels*-*-*-*-*-*-*-*-*
// ===========================================
//
// By default the number of contour levels is set to 20.
//
// if argument levels = 0 or missing, equidistant contours are computed
//
Int_t level;
ResetBit(kUserContour);
if (nlevels <=0 ) {
fContour.Set(0);
return;
}
fContour.Set(nlevels);
// - Contour levels are specified
if (levels) {
SetBit(kUserContour);
for (level=0; level<nlevels; level++) fContour.fArray[level] = levels[level];
} else {
// - contour levels are computed automatically as equidistant contours
Double_t zmin = GetMinimum();
Double_t zmax = GetMaximum();
if ((zmin == zmax) && (zmin != 0)) {
zmax += 0.01*TMath::Abs(zmax);
zmin -= 0.01*TMath::Abs(zmin);
}
Double_t dz = (zmax-zmin)/Double_t(nlevels);
if (gPad && gPad->GetLogz()) {
if (zmax <= 0) return;
if (zmin <= 0) zmin = 0.001*zmax;
zmin = TMath::Log10(zmin);
zmax = TMath::Log10(zmax);
dz = (zmax-zmin)/Double_t(nlevels);
}
for (level=0; level<nlevels; level++) {
fContour.fArray[level] = zmin + dz*Double_t(level);
}
}
}
//______________________________________________________________________________
void TH1::SetContourLevel(Int_t level, Double_t value)
{
// -*-*-*-*-*-*-*-*-*Set value for one contour level*-*-*-*-*-*-*-*-*-*-*-*
// ===============================
if (level <0 || level >= fContour.fN) return;
SetBit(kUserContour);
fContour.fArray[level] = value;
}
//______________________________________________________________________________
Double_t TH1::GetMaximum(Double_t maxval) const
{
// Return maximum value smaller than maxval of bins in the range*-*-*-*-*-*
if (fMaximum != -1111) return fMaximum;
Int_t bin, binx, biny, binz;
Int_t xfirst = fXaxis.GetFirst();
Int_t xlast = fXaxis.GetLast();
Int_t yfirst = fYaxis.GetFirst();
Int_t ylast = fYaxis.GetLast();
Int_t zfirst = fZaxis.GetFirst();
Int_t zlast = fZaxis.GetLast();
Double_t maximum = -FLT_MAX, value;
for (binz=zfirst;binz<=zlast;binz++) {
for (biny=yfirst;biny<=ylast;biny++) {
for (binx=xfirst;binx<=xlast;binx++) {
bin = GetBin(binx,biny,binz);
value = GetBinContent(bin);
if (value > maximum && value < maxval) maximum = value;
}
}
}
return maximum;
}
//______________________________________________________________________________
Int_t TH1::GetMaximumBin() const
{
// -*-*-*-*-*Return location of bin with maximum value in the range*-*
// ======================================================
Int_t locmax, locmay, locmaz;
return GetMaximumBin(locmax, locmay, locmaz);
}
//______________________________________________________________________________
Int_t TH1::GetMaximumBin(Int_t &locmax, Int_t &locmay, Int_t &locmaz) const
{
// -*-*-*-*-*Return location of bin with maximum value in the range*-*
// ======================================================
Int_t bin, binx, biny, binz;
Int_t locm;
Int_t xfirst = fXaxis.GetFirst();
Int_t xlast = fXaxis.GetLast();
Int_t yfirst = fYaxis.GetFirst();
Int_t ylast = fYaxis.GetLast();
Int_t zfirst = fZaxis.GetFirst();
Int_t zlast = fZaxis.GetLast();
Double_t maximum = -FLT_MAX, value;
locm = locmax = locmay = locmaz = 0;
for (binz=zfirst;binz<=zlast;binz++) {
for (biny=yfirst;biny<=ylast;biny++) {
for (binx=xfirst;binx<=xlast;binx++) {
bin = GetBin(binx,biny,binz);
value = GetBinContent(bin);
if (value > maximum) {
maximum = value;
locm = bin;
locmax = binx;
locmay = biny;
locmaz = binz;
}
}
}
}
return locm;
}
//______________________________________________________________________________
Double_t TH1::GetMinimum(Double_t minval) const
{
// Return minimum value greater than minval of bins in the range
if (fMinimum != -1111) return fMinimum;
Int_t bin, binx, biny, binz;
Int_t xfirst = fXaxis.GetFirst();
Int_t xlast = fXaxis.GetLast();
Int_t yfirst = fYaxis.GetFirst();
Int_t ylast = fYaxis.GetLast();
Int_t zfirst = fZaxis.GetFirst();
Int_t zlast = fZaxis.GetLast();
Double_t minimum=FLT_MAX, value;
for (binz=zfirst;binz<=zlast;binz++) {
for (biny=yfirst;biny<=ylast;biny++) {
for (binx=xfirst;binx<=xlast;binx++) {
bin = GetBin(binx,biny,binz);
value = GetBinContent(bin);
if (value < minimum && value > minval) minimum = value;
}
}
}
return minimum;
}
//______________________________________________________________________________
Int_t TH1::GetMinimumBin() const
{
// -*-*-*-*-*Return location of bin with minimum value in the range*-*
// ======================================================
Int_t locmix, locmiy, locmiz;
return GetMinimumBin(locmix, locmiy, locmiz);
}
//______________________________________________________________________________
Int_t TH1::GetMinimumBin(Int_t &locmix, Int_t &locmiy, Int_t &locmiz) const
{
// -*-*-*-*-*Return location of bin with minimum value in the range*-*
// ======================================================
Int_t bin, binx, biny, binz;
Int_t locm;
Int_t xfirst = fXaxis.GetFirst();
Int_t xlast = fXaxis.GetLast();
Int_t yfirst = fYaxis.GetFirst();
Int_t ylast = fYaxis.GetLast();
Int_t zfirst = fZaxis.GetFirst();
Int_t zlast = fZaxis.GetLast();
Double_t minimum = FLT_MAX, value;
locm = locmix = locmiy = locmiz = 0;
for (binz=zfirst;binz<=zlast;binz++) {
for (biny=yfirst;biny<=ylast;biny++) {
for (binx=xfirst;binx<=xlast;binx++) {
bin = GetBin(binx,biny,binz);
value = GetBinContent(bin);
if (value < minimum) {
minimum = value;
locm = bin;
locmix = binx;
locmiy = biny;
locmiz = binz;
}
}
}
}
return locm;
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, Axis_t xmin, Axis_t xmax)
{
// -*-*-*-*-*-*-*Redefine x axis parameters*-*-*-*-*-*-*-*-*-*-*-*
// ===========================
// The X axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
if (GetDimension() != 1) {
Error("SetBins","Operation only valid for 1-d histograms");
return;
}
fXaxis.SetRange(0,0);
fXaxis.Set(nx,xmin,xmax);
fYaxis.Set(1,0,1);
fZaxis.Set(1,0,1);
fNcells = nx+2;
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, const Axis_t *xBins)
{
// -*-*-*-*-*-*-*Redefine x axis parameters with variable bin sizes *-*-*-*-*-*-*-*-*-*
// ===================================================
// The X axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
// xBins is supposed to be of length nx+1
if (GetDimension() != 1) {
Error("SetBins","Operation only valid for 1-d histograms");
return;
}
fXaxis.SetRange(0,0);
fXaxis.Set(nx,xBins);
fYaxis.Set(1,0,1);
fZaxis.Set(1,0,1);
fNcells = nx+2;
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, Axis_t xmin, Axis_t xmax, Int_t ny, Axis_t ymin, Axis_t ymax)
{
// -*-*-*-*-*-*-*Redefine x and y axis parameters*-*-*-*-*-*-*-*-*-*-*-*
// =================================
// The X and Y axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
if (GetDimension() != 2) {
Error("SetBins","Operation only valid for 2-d histograms");
return;
}
fXaxis.SetRange(0,0);
fYaxis.SetRange(0,0);
fXaxis.Set(nx,xmin,xmax);
fYaxis.Set(ny,ymin,ymax);
fZaxis.Set(1,0,1);
fNcells = (nx+2)*(ny+2);
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, const Axis_t *xBins, Int_t ny, const Axis_t *yBins)
{
// -*-*-*-*-*-*-*Redefine x and y axis parameters with variable bin sizes *-*-*-*-*-*-*-*-*
// =========================================================
// The X and Y axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
// xBins is supposed to be of length nx+1, yBins is supposed to be of length ny+1
if (GetDimension() != 2) {
Error("SetBins","Operation only valid for 2-d histograms");
return;
}
fXaxis.SetRange(0,0);
fYaxis.SetRange(0,0);
fXaxis.Set(nx,xBins);
fYaxis.Set(ny,yBins);
fZaxis.Set(1,0,1);
fNcells = (nx+2)*(ny+2);
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, Axis_t xmin, Axis_t xmax, Int_t ny, Axis_t ymin, Axis_t ymax, Int_t nz, Axis_t zmin, Axis_t zmax)
{
// -*-*-*-*-*-*-*Redefine x, y and z axis parameters*-*-*-*-*-*-*-*-*-*-*-*
// ====================================
// The X, Y and Z axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
if (GetDimension() != 3) {
Error("SetBins","Operation only valid for 3-d histograms");
return;
}
fXaxis.SetRange(0,0);
fYaxis.SetRange(0,0);
fZaxis.SetRange(0,0);
fXaxis.Set(nx,xmin,xmax);
fYaxis.Set(ny,ymin,ymax);
fZaxis.Set(nz,zmin,zmax);
fNcells = (nx+2)*(ny+2)*(nz+2);
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetMaximum(Double_t maximum)
{
// -*-*-*-*-*-*-*Set the maximum value for the Y axis*-*-*-*-*-*-*-*-*-*-*-*
// ====================================
// By default the maximum value is automatically set to the maximum
// bin content plus a margin of 10 per cent.
// Use TH1::GetMaximum to find the maximum value of an histogram
// Use TH1::GetMaximumBin to find the bin with the maximum value of an histogram
//
fMaximum = maximum;
}
//______________________________________________________________________________
void TH1::SetMinimum(Double_t minimum)
{
// -*-*-*-*-*-*-*Set the minimum value for the Y axis*-*-*-*-*-*-*-*-*-*-*-*
// ====================================
// By default the minimum value is automatically set to zero if all bin contents
// are positive or the minimum - 10 per cent otherwise.
// Use TH1::GetMinimum to find the minimum value of an histogram
// Use TH1::GetMinimumBin to find the bin with the minimum value of an histogram
//
fMinimum = minimum;
}
//______________________________________________________________________________
void TH1::SetDirectory(TDirectory *dir)
{
// By default when an histogram is created, it is added to the list
// of histogram objects in the current directory in memory.
// Remove reference to this histogram from current directory and add
// reference to new directory dir. dir can be 0 in which case the
// histogram does not belong to any directory.
if (fDirectory == dir) return;
if (fDirectory) fDirectory->GetList()->Remove(this);
fDirectory = dir;
if (fDirectory) fDirectory->GetList()->Add(this);
}
//______________________________________________________________________________
void TH1::SetError(const Stat_t *error)
{
// -*-*-*-*-*-*-*Replace bin errors by values in array error*-*-*-*-*-*-*-*-*
// ===========================================
Int_t bin;
Stat_t binerror;
for (bin=0; bin<fNcells; bin++) {
binerror = error[bin];
SetBinError(bin, binerror);
}
}
//______________________________________________________________________________
void TH1::SetName(const char *name)
{
// Change the name of this histogram
//
// Histograms are named objects in a THashList.
// We must update the hashlist if we change the name
if (fDirectory) fDirectory->GetList()->Remove(this);
fName = name;
if (fDirectory) fDirectory->GetList()->Add(this);
}
//______________________________________________________________________________
void TH1::SetNameTitle(const char *name, const char *title)
{
// Change the name and title of this histogram
//
// Histograms are named objects in a THashList.
// We must update the hashlist if we change the name
if (fDirectory) fDirectory->GetList()->Remove(this);
fName = name;
SetTitle(title);
if (fDirectory) fDirectory->GetList()->Add(this);
}
//______________________________________________________________________________
void TH1::SetStats(Bool_t stats)
{
// -*-*-*-*-*-*-*Set statistics option on/off
// ============================
// By default, the statistics box is drawn.
// The paint options can be selected via gStyle->SetOptStats.
// This function sets/resets the kNoStats bin in the histogram object.
// It has priority over the Style option.
ResetBit(kNoStats);
if (!stats) {
SetBit(kNoStats);
//remove the "stats" object from the list of functions
if (fFunctions) delete fFunctions->FindObject("stats");
}
}
//______________________________________________________________________________
void TH1::Sumw2()
{
// -*-*-*Create structure to store sum of squares of weights*-*-*-*-*-*-*-*
// ===================================================
//
// if histogram is already filled, the sum of squares of weights
// is filled with the existing bin contents
//
// The error per bin will be computed as sqrt(sum of squares of weight)
// for each bin.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (fSumw2.fN) {
Warning("Sumw2","Sum of squares of weights structure already created");
return;
}
fSumw2.Set(fNcells);
for (Int_t bin=0; bin<fNcells; bin++) {
fSumw2.fArray[bin] = GetBinContent(bin);
}
}
//______________________________________________________________________________
TF1 *TH1::GetFunction(const char *name) const
{
// -*-*-*Return pointer to function with name*-*-*-*-*-*-*-*-*-*-*-*-*
// ===================================
//
// Functions such as TH1::Fit store the fitted function in the list of
// functions of this histogram.
return (TF1*)fFunctions->FindObject(name);
}
//______________________________________________________________________________
Stat_t TH1::GetBinError(Int_t bin) const
{
// -*-*-*-*-*Return value of error associated to bin number bin*-*-*-*-*
// ==================================================
//
// if the sum of squares of weights has been defined (via Sumw2),
// this function returns the sqrt(sum of w2).
// otherwise it returns the sqrt(contents) for this bin.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (fBuffer) ((TH1*)this)->BufferEmpty();
if (fSumw2.fN) return TMath::Sqrt(fSumw2.fArray[bin]);
Stat_t error2 = TMath::Abs(GetBinContent(bin));
return TMath::Sqrt(error2);
}
//______________________________________________________________________________
Stat_t TH1::GetBinError(Int_t binx, Int_t biny) const
{
// -*-*-*-*-*Return error of bin number binx, biny
// =====================================
// NB: Function to be called for 2-d histograms only
Int_t bin = GetBin(binx,biny);
return GetBinError(bin);
}
//______________________________________________________________________________
Stat_t TH1::GetBinError(Int_t binx, Int_t biny, Int_t binz) const
{
// -*-*-*-*-*Return error of bin number binx,biny,binz
// =========================================
// NB: Function to be called for 3-d histograms only
Int_t bin = GetBin(binx,biny,binz);
return GetBinError(bin);
}
//______________________________________________________________________________
Stat_t TH1::GetCellContent(Int_t binx, Int_t biny) const
{
// -*-*-*-*-*Return content of bin number binx, biny
// =====================================
// NB: Function to be called for 2-d histograms only
Int_t bin = GetBin(binx,biny);
return GetBinContent(bin);
}
//______________________________________________________________________________
Stat_t TH1::GetCellError(Int_t binx, Int_t biny) const
{
// -*-*-*-*-*Return error of bin number binx, biny
// =====================================
// NB: Function to be called for 2-d histograms only
Int_t bin = GetBin(binx,biny);
return GetBinError(bin);
}
//______________________________________________________________________________
void TH1::SetBinError(Int_t bin, Stat_t error)
{
// see convention for numbering bins in TH1::GetBin
if (!fSumw2.fN) Sumw2();
if (bin <0 || bin>= fSumw2.fN) return;
fSumw2.fArray[bin] = error*error;
}
//______________________________________________________________________________
void TH1::SetBinContent(Int_t binx, Int_t biny, Stat_t content)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
SetBinContent(biny*(fXaxis.GetNbins()+2) + binx,content);
}
//______________________________________________________________________________
void TH1::SetBinContent(Int_t binx, Int_t biny, Int_t binz, Stat_t content)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
if (binz <0 || binz>fZaxis.GetNbins()+1) return;
Int_t bin = GetBin(binx,biny,binz);
SetBinContent(bin,content);
}
//______________________________________________________________________________
void TH1::SetCellContent(Int_t binx, Int_t biny, Stat_t content)
{
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
SetBinContent(biny*(fXaxis.GetNbins()+2) + binx,content);
}
//______________________________________________________________________________
void TH1::SetBinError(Int_t binx, Int_t biny, Stat_t error)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
SetBinError(biny*(fXaxis.GetNbins()+2) + binx,error);
}
//______________________________________________________________________________
void TH1::SetBinError(Int_t binx, Int_t biny, Int_t binz, Stat_t error)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
if (binz <0 || binz>fZaxis.GetNbins()+1) return;
Int_t bin = GetBin(binx,biny,binz);
SetBinError(bin,error);
}
//______________________________________________________________________________
void TH1::SetCellError(Int_t binx, Int_t biny, Stat_t error)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
if (!fSumw2.fN) Sumw2();
Int_t bin = biny*(fXaxis.GetNbins()+2) + binx;
fSumw2.fArray[bin] = error*error;
}
//______________________________________________________________________________
void TH1::SetBinContent(Int_t, Stat_t)
{
// see convention for numbering bins in TH1::GetBin
AbstractMethod("SetBinContent");
}
ClassImp(TH1C)
//______________________________________________________________________________
// TH1C methods
//______________________________________________________________________________
TH1C::TH1C(): TH1(), TArrayC()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1C::TH1C(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type char (one byte per channel)
// ==========================================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayC::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1C::TH1C(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type char (one byte per channel)
// ==========================================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayC::Set(fNcells);
}
//______________________________________________________________________________
TH1C::TH1C(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type char (one byte per channel)
// ==========================================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayC::Set(fNcells);
}
//______________________________________________________________________________
TH1C::~TH1C()
{
}
//______________________________________________________________________________
TH1C::TH1C(const TH1C &h1c) : TH1(), TArrayC()
{
((TH1C&)h1c).Copy(*this);
}
//______________________________________________________________________________
void TH1C::AddBinContent(Int_t bin)
{
// -*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
if (fArray[bin] < 127) fArray[bin]++;
}
//______________________________________________________________________________
void TH1C::AddBinContent(Int_t bin, Stat_t w)
{
// -*-*-*-*-*-*-*-*Increment bin content by w*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
Int_t newval = fArray[bin] + Int_t(w);
if (newval > -128 && newval < 128) {fArray[bin] = Char_t(newval); return;}
if (newval < -127) fArray[bin] = -127;
if (newval > 127) fArray[bin] = 127;
}
//______________________________________________________________________________
void TH1C::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayC::Copy((TH1C&)newth1);
}
//______________________________________________________________________________
TH1 *TH1C::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1C *newth1 = (TH1C*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1C::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1C*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1C::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayC::Reset();
}
//______________________________________________________________________________
void TH1C::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = Char_t (content);
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = Char_t (content);
fEntries++;
}
//______________________________________________________________________________
void TH1C::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayC::Set(n);
}
//______________________________________________________________________________
TH1C& TH1C::operator=(const TH1C &h1)
{
if (this != &h1) ((TH1C&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1C operator*(Double_t c1, const TH1C &h1)
{
TH1C hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1C operator+(const TH1C &h1, const TH1C &h2)
{
TH1C hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1C operator-(const TH1C &h1, const TH1C &h2)
{
TH1C hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1C operator*(const TH1C &h1, const TH1C &h2)
{
TH1C hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1C operator/(const TH1C &h1, const TH1C &h2)
{
TH1C hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
ClassImp(TH1S)
//______________________________________________________________________________
// TH1S methods
//______________________________________________________________________________
TH1S::TH1S(): TH1(), TArrayS()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1S::TH1S(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type short
// ====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayS::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1S::TH1S(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type short
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayS::Set(fNcells);
}
//______________________________________________________________________________
TH1S::TH1S(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type short
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayS::Set(fNcells);
}
//______________________________________________________________________________
TH1S::~TH1S()
{
}
//______________________________________________________________________________
TH1S::TH1S(const TH1S &h1s) : TH1(), TArrayS()
{
((TH1S&)h1s).Copy(*this);
}
//______________________________________________________________________________
void TH1S::AddBinContent(Int_t bin)
{
// -*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
if (fArray[bin] < 32767) fArray[bin]++;
}
//______________________________________________________________________________
void TH1S::AddBinContent(Int_t bin, Stat_t w)
{
// Increment bin content by w
// ==========================
Int_t newval = fArray[bin] + Int_t(w);
if (newval > -32768 && newval < 32768) {fArray[bin] = Short_t(newval); return;}
if (newval < -32767) fArray[bin] = -32767;
if (newval > 32767) fArray[bin] = 32767;
}
//______________________________________________________________________________
void TH1S::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayS::Copy((TH1S&)newth1);
}
//______________________________________________________________________________
TH1 *TH1S::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1S *newth1 = (TH1S*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1S::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1S*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1S::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayS::Reset();
}
//______________________________________________________________________________
void TH1S::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = Short_t (content);
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = Short_t (content);
fEntries++;
}
//______________________________________________________________________________
void TH1S::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayS::Set(n);
}
//______________________________________________________________________________
TH1S& TH1S::operator=(const TH1S &h1)
{
if (this != &h1) ((TH1S&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1S operator*(Double_t c1, const TH1S &h1)
{
TH1S hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1S operator+(const TH1S &h1, const TH1S &h2)
{
TH1S hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1S operator-(const TH1S &h1, const TH1S &h2)
{
TH1S hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1S operator*(const TH1S &h1, const TH1S &h2)
{
TH1S hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1S operator/(const TH1S &h1, const TH1S &h2)
{
TH1S hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
ClassImp(TH1I)
//______________________________________________________________________________
// TH1I methods
//______________________________________________________________________________
TH1I::TH1I(): TH1(), TArrayI()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1I::TH1I(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type integer
// ====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayI::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1I::TH1I(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type integer
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayI::Set(fNcells);
}
//______________________________________________________________________________
TH1I::TH1I(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type integer
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayI::Set(fNcells);
}
//______________________________________________________________________________
TH1I::~TH1I()
{
}
//______________________________________________________________________________
TH1I::TH1I(const TH1I &h1i) : TH1(), TArrayI()
{
((TH1I&)h1i).Copy(*this);
}
//______________________________________________________________________________
void TH1I::AddBinContent(Int_t bin)
{
// -*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
if (fArray[bin] < 2147483647) fArray[bin]++;
}
//______________________________________________________________________________
void TH1I::AddBinContent(Int_t bin, Stat_t w)
{
// Increment bin content by w
// ==========================
Int_t newval = fArray[bin] + Int_t(w);
if (newval > -2147483647 && newval < 2147483647) {fArray[bin] = Int_t(newval); return;}
if (newval < -2147483647) fArray[bin] = -2147483647;
if (newval > 2147483647) fArray[bin] = 2147483647;
}
//______________________________________________________________________________
void TH1I::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayI::Copy((TH1I&)newth1);
}
//______________________________________________________________________________
TH1 *TH1I::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1I *newth1 = (TH1I*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1I::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1I*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1I::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayI::Reset();
}
//______________________________________________________________________________
void TH1I::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = Int_t (content);
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = Int_t (content);
fEntries++;
}
//______________________________________________________________________________
void TH1I::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayI::Set(n);
}
//______________________________________________________________________________
TH1I& TH1I::operator=(const TH1I &h1)
{
if (this != &h1) ((TH1I&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1I operator*(Double_t c1, const TH1I &h1)
{
TH1I hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1I operator+(const TH1I &h1, const TH1I &h2)
{
TH1I hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1I operator-(const TH1I &h1, const TH1I &h2)
{
TH1I hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1I operator*(const TH1I &h1, const TH1I &h2)
{
TH1I hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1I operator/(const TH1I &h1, const TH1I &h2)
{
TH1I hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
ClassImp(TH1F)
//______________________________________________________________________________
// TH1F methods
//______________________________________________________________________________
TH1F::TH1F(): TH1(), TArrayF()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1F::TH1F(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type float
// ====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayF::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1F::TH1F(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type float
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayF::Set(fNcells);
}
//______________________________________________________________________________
TH1F::TH1F(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type float
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayF::Set(fNcells);
}
//______________________________________________________________________________
TH1F::TH1F(const TVectorF &v)
: TH1("TVectorF","",v.GetNrows(),0,v.GetNrows())
{
// Create a histogram from a TVectorF
// by default the histogram name is "TVectorF" and title = ""
TArrayF::Set(fNcells);
fDimension = 1;
for (Int_t i=0;i<v.GetNrows();i++) {
SetBinContent(i+1,v(i));
}
TArrayF::Set(fNcells);
}
//______________________________________________________________________________
TH1F::TH1F(const TH1F &h) : TH1(), TArrayF()
{
((TH1F&)h).Copy(*this);
}
//______________________________________________________________________________
TH1F::~TH1F()
{
}
//______________________________________________________________________________
void TH1F::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayF::Copy((TH1F&)newth1);
}
//______________________________________________________________________________
TH1 *TH1F::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1F *newth1 = (TH1F*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1F::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1F*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1F::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayF::Reset();
}
//______________________________________________________________________________
void TH1F::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = Float_t (content);
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = Float_t (content);
fEntries++;
}
//______________________________________________________________________________
void TH1F::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayF::Set(n);
}
//______________________________________________________________________________
TH1F& TH1F::operator=(const TH1F &h1)
{
if (this != &h1) ((TH1F&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1F operator*(Double_t c1, const TH1F &h1)
{
TH1F hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1F operator+(const TH1F &h1, const TH1F &h2)
{
TH1F hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1F operator-(const TH1F &h1, const TH1F &h2)
{
TH1F hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1F operator*(const TH1F &h1, const TH1F &h2)
{
TH1F hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1F operator/(const TH1F &h1, const TH1F &h2)
{
TH1F hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
ClassImp(TH1D)
//______________________________________________________________________________
// TH1D methods
//______________________________________________________________________________
TH1D::TH1D(): TH1(), TArrayD()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1D::TH1D(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type double
// =====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayD::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1D::TH1D(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type double
// =====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayD::Set(fNcells);
}
//______________________________________________________________________________
TH1D::TH1D(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type double
// =====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayD::Set(fNcells);
}
//______________________________________________________________________________
TH1D::TH1D(const TVectorD &v)
: TH1("TVectorD","",v.GetNrows(),0,v.GetNrows())
{
// Create a histogram from a TVectorD
// by default the histogram name is "TVectorD" and title = ""
TArrayD::Set(fNcells);
fDimension = 1;
for (Int_t i=0;i<v.GetNrows();i++) {
SetBinContent(i+1,v(i));
}
TArrayD::Set(fNcells);
}
//______________________________________________________________________________
TH1D::~TH1D()
{
}
//______________________________________________________________________________
TH1D::TH1D(const TH1D &h1d) : TH1(), TArrayD()
{
((TH1D&)h1d).Copy(*this);
}
//______________________________________________________________________________
void TH1D::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayD::Copy((TH1D&)newth1);
}
//______________________________________________________________________________
TH1 *TH1D::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1D *newth1 = (TH1D*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1D::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1D*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1D::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayD::Reset();
}
//______________________________________________________________________________
void TH1D::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = content;
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = content;
fEntries++;
}
//______________________________________________________________________________
void TH1D::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayD::Set(n);
}
//______________________________________________________________________________
TH1D& TH1D::operator=(const TH1D &h1)
{
if (this != &h1) ((TH1D&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1D operator*(Double_t c1, const TH1D &h1)
{
TH1D hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1D operator+(const TH1D &h1, const TH1D &h2)
{
TH1D hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1D operator-(const TH1D &h1, const TH1D &h2)
{
TH1D hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1D operator*(const TH1D &h1, const TH1D &h2)
{
TH1D hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1D operator/(const TH1D &h1, const TH1D &h2)
{
TH1D hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1 *R__H(Int_t hid)
{
//return pointer to histogram with name
// hid if id >=0
// h_id if id <0
char hname[20];
if(hid >= 0) sprintf(hname,"h%d",hid);
else sprintf(hname,"h_%d",hid);
return (TH1*)gDirectory->Get(hname);
}
//______________________________________________________________________________
TH1 *R__H(const char * hname)
{
//return pointer to histogram with name hname
return (TH1*)gDirectory->Get(hname);
}
*/
//
TF1 *gF1=0; //left for back compatibility (use TVirtualFitter::GetUserFunc instead)
const Int_t kNstat = 11;
Int_t TH1::fgBufferSize = 1000;
Bool_t TH1::fgAddDirectory = kTRUE;
Bool_t TH1::fgStatOverflows= kFALSE;
extern void H1InitGaus();
extern void H1InitExpo();
extern void H1InitPolynom();
extern void H1LeastSquareFit(Int_t n, Int_t m, Double_t *a);
extern void H1LeastSquareLinearFit(Int_t ndata, Double_t &a0, Double_t &a1, Int_t &ifail);
extern void H1LeastSquareSeqnd(Int_t n, Double_t *a, Int_t idim, Int_t &ifail, Int_t k, Double_t *b);
ClassImp(TH1)
//______________________________________________________________________________
TH1::TH1(): TNamed(), TAttLine(), TAttFill(), TAttMarker()
{
// -*-*-*-*-*-*-*-*-*Histogram default constructor*-*-*-*-*-*-*-*-*-*-*-*-*
// =============================
fDirectory = 0;
fFunctions = new TList;
fNcells = 0;
fIntegral = 0;
fPainter = 0;
fEntries = 0;
fNormFactor = 0;
fTsumw = fTsumw2=fTsumwx=fTsumwx2=0;
fMaximum = -1111;
fMinimum = -1111;
fBufferSize = 0;
fBuffer = 0;
fXaxis.SetName("xaxis");
fYaxis.SetName("yaxis");
fZaxis.SetName("zaxis");
fXaxis.SetParent(this);
fYaxis.SetParent(this);
fZaxis.SetParent(this);
UseCurrentStyle();
}
//______________________________________________________________________________
TH1::~TH1()
{
// -*-*-*-*-*-*-*-*-*Histogram default destructor*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ============================
//TH1 *junk = 0;
//junk->SetLineColor(0);
if (!TestBit(kNotDeleted)) return;
if (fIntegral) {delete [] fIntegral; fIntegral = 0;}
if (fBuffer) {delete [] fBuffer; fBuffer = 0;}
if (fFunctions) {
fFunctions->SetBit(kInvalidObject);
TObject *obj;
//special logic to support the case where the same object is
//added multiple times in fFunctions.
//This case happens when the same object is added with different
//drawing modes
//In the loop below we must be careful with objects (eg TCutG) that may
// have been added to the list of functions of several histograms
//and may have been already deleted.
while ((obj = fFunctions->First())) {
while(fFunctions->Remove(obj));
if (!obj->TestBit(kNotDeleted)) break;
delete obj;
}
delete fFunctions;
}
if (fDirectory) {
if (!fDirectory->TestBit(TDirectory::kCloseDirectory))
fDirectory->GetList()->Remove(this);
}
fFunctions = 0;
fDirectory = 0;
delete fPainter;
}
//______________________________________________________________________________
TH1::TH1(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
:TNamed(name,title), TAttLine(), TAttFill(), TAttMarker()
{
// -*-*-*-*-*-*-*Normal constructor for fix bin size histograms*-*-*-*-*-*-*
// ==============================================
//
// Creates the main histogram structure:
// name : name of histogram (avoid blanks)
// title : histogram title
// if title is of the form "stringt;stringx;stringy;stringz"
// the histogram title is set to stringt,
// the x axis title to stringy, the y axis title to stringy,etc
// nbins : number of bins
// xlow : low edge of first bin
// xup : upper edge of last bin (not included in last bin)
//
// When an histogram is created, it is automatically added to the list
// of special objects in the current directory.
// To find the pointer to this histogram in the current directory
// by its name, do:
// TH1F *h1 = (TH1F*)gDirectory->FindObject(name);
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Build();
if (nbins <= 0) nbins = 1;
fXaxis.Set(nbins,xlow,xup);
fNcells = fXaxis.GetNbins()+2;
}
//______________________________________________________________________________
TH1::TH1(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
:TNamed(name,title), TAttLine(), TAttFill(), TAttMarker()
{
// -*-*-*-*-*Normal constructor for variable bin size histograms*-*-*-*-*-*-*
// ===================================================
//
// Creates the main histogram structure:
// name : name of histogram (avoid blanks)
// title : histogram title
// if title is of the form "stringt;stringx;stringy;stringz"
// the histogram title is set to stringt,
// the x axis title to stringy, the y axis title to stringy,etc
// nbins : number of bins
// xbins : array of low-edges for each bin
// This is an array of size nbins+1
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Build();
if (nbins <= 0) nbins = 1;
if (xbins) fXaxis.Set(nbins,xbins);
else fXaxis.Set(nbins,0,1);
fNcells = fXaxis.GetNbins()+2;
}
//______________________________________________________________________________
TH1::TH1(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
:TNamed(name,title), TAttLine(), TAttFill(), TAttMarker()
{
// -*-*-*-*-*Normal constructor for variable bin size histograms*-*-*-*-*-*-*
// ===================================================
//
// Creates the main histogram structure:
// name : name of histogram (avoid blanks)
// title : histogram title
// if title is of the form "stringt;stringx;stringy;stringz"
// the histogram title is set to stringt,
// the x axis title to stringy, the y axis title to stringy,etc
// nbins : number of bins
// xbins : array of low-edges for each bin
// This is an array of size nbins+1
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Build();
if (nbins <= 0) nbins = 1;
if (xbins) fXaxis.Set(nbins,xbins);
else fXaxis.Set(nbins,0,1);
fNcells = fXaxis.GetNbins()+2;
}
//______________________________________________________________________________
TH1::TH1(const TH1 &h) : TNamed(), TAttLine(), TAttFill(), TAttMarker()
{
// Copy constructor.
// The list of functions is not copied. (Use Clone if needed)
Copy((TObject&)h);
}
//______________________________________________________________________________
Bool_t TH1::AddDirectoryStatus()
{
//static function: cannot be inlined on Windows/NT
return fgAddDirectory;
}
//______________________________________________________________________________
void TH1::Browse(TBrowser *b)
{
Draw(b ? b->GetDrawOption() : "");
gPad->Update();
}
//______________________________________________________________________________
void TH1::Build()
{
// -*-*-*-*-*-*-*-*Creates histogram basic data structure*-*-*-*-*-*-*-*-*-*
// ======================================
fDirectory = 0;
fPainter = 0;
fIntegral = 0;
fEntries = 0;
fNormFactor = 0;
fTsumw = fTsumw2=fTsumwx=fTsumwx2=0;
fMaximum = -1111;
fMinimum = -1111;
fBufferSize = 0;
fBuffer = 0;
fXaxis.SetName("xaxis");
fYaxis.SetName("yaxis");
fZaxis.SetName("zaxis");
fYaxis.Set(1,0.,1.);
fZaxis.Set(1,0.,1.);
fXaxis.SetParent(this);
fYaxis.SetParent(this);
fZaxis.SetParent(this);
SetTitle(fTitle.Data());
fFunctions = new TList;
UseCurrentStyle();
if (fgAddDirectory && gDirectory) {
if (!gDirectory->GetList()) {
Warning("Build","Current directory is not a valid directory");
return;
}
TH1 *hold = (TH1*)gDirectory->GetList()->FindObject(GetName());
if (hold) {
Warning("Build","Replacing existing histogram: %s (Potential memory leak).",GetName());
gDirectory->GetList()->Remove(hold);
hold->SetDirectory(0);
// delete hold;
}
gDirectory->Append(this);
fDirectory = gDirectory;
}
}
//______________________________________________________________________________
void TH1::Add(TF1 *f1, Double_t c1, Option_t *option)
{
// Performs the operation: this = this + c1*f1
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
//
// By default, the function is computed at the centre of the bin.
// if option "I" is specified (1-d histogram only), the integral of the
// function in each bin is used instead of the value of the function at
// the centre of the bin.
// Only bins inside the function range are recomputed.
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Add
if (!f1) {
Error("Add","Attempt to add a non-existing function");
return;
}
TString opt = option;
opt.ToLower();
Bool_t integral = kFALSE;
if (opt.Contains("i") && fDimension ==1) integral = kTRUE;
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// - Add statistics
Stat_t s1[10];
Int_t i;
for (i=0;i<10;i++) {s1[i] = 0;}
PutStats(s1);
SetMinimum();
SetMaximum();
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu=0;
Double_t xx[3];
Double_t *params = 0;
f1->InitArgs(xx,params);
for (binz=0;binz<=nbinsz+1;binz++) {
xx[2] = fZaxis.GetBinCenter(binz);
for (biny=0;biny<=nbinsy+1;biny++) {
xx[1] = fYaxis.GetBinCenter(biny);
for (binx=0;binx<=nbinsx+1;binx++) {
xx[0] = fXaxis.GetBinCenter(binx);
if (!f1->IsInside(xx)) continue;
TF1::RejectPoint(kFALSE);
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
if (integral) {
xx[0] = fXaxis.GetBinLowEdge(binx);
cu = c1*f1->EvalPar(xx);
cu += c1*f1->Integral(fXaxis.GetBinLowEdge(binx),fXaxis.GetBinUpEdge(binx))*fXaxis.GetBinWidth(binx);
} else {
cu = c1*f1->EvalPar(xx);
}
if (TF1::RejectedPoint()) continue;
Double_t error1 = GetBinError(bin);
AddBinContent(bin,cu);
if (fSumw2.fN) {
//errors are unchanged: error on f1 assumed 0
fSumw2.fArray[bin] = error1*error1;
}
}
}
}
}
//______________________________________________________________________________
void TH1::Add(const TH1 *h1, Double_t c1)
{
// Performs the operation: this = this + c1*h1
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
// Note that if h1 has Sumw2 set, Sumw2 is automatically called for this
// if not already set.
//
// IMPORTANT NOTE1: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Add
//
// IMPORTANT NOTE2: if h1 has a normalisation factor, the normalisation factor
// is used , ie this = this + c1*factor*h1
// Use the other TH1::Add function if you do not want this feature
if (!h1) {
Error("Add","Attempt to add a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()) {
Error("Add","Attempt to add histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Add","Attempt to add histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 has Sumw2 set
if (fSumw2.fN == 0 && h1->GetSumw2N() != 0) Sumw2();
// - Add statistics
fEntries += c1*h1->GetEntries();
Stat_t s1[kNstat], s2[kNstat];
Int_t i;
for (i=0;i<kNstat;i++) {s1[i] = s2[i] = 0;}
GetStats(s1);
h1->GetStats(s2);
for (i=0;i<kNstat;i++) {
if (i == 1) s1[i] += c1*c1*s2[i];
else s1[i] += c1*s2[i];
}
PutStats(s1);
SetMinimum();
SetMaximum();
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu;
Double_t factor =1;
if (h1->GetNormFactor() != 0) factor = h1->GetNormFactor()/h1->GetSumOfWeights();;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
cu = c1*factor*h1->GetBinContent(bin);
AddBinContent(bin,cu);
if (fSumw2.fN) {
Double_t error1 = factor*h1->GetBinError(bin);
fSumw2.fArray[bin] += c1*c1*error1*error1;
}
}
}
}
}
//______________________________________________________________________________
void TH1::Add(const TH1 *h1, const TH1 *h2, Double_t c1, Double_t c2)
{
// -*-*-*Replace contents of this histogram by the addition of h1 and h2*-*-*
// ===============================================================
//
// this = c1*h1 + c2*h2
// if errors are defined (see TH1::Sumw2), errors are also recalculated
// Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this
// if not already set.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Add
if (!h1 || !h2) {
Error("Add","Attempt to add a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()
|| nbinsx != h2->GetNbinsX() || nbinsy != h2->GetNbinsY() || nbinsz != h2->GetNbinsZ()) {
Error("Add","Attempt to add histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Add","Attempt to add histograms with different axis limits");
}
if (fXaxis.GetXmin() != h2->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h2->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h2->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h2->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h2->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h2->fZaxis.GetXmax()) {
Warning("Add","Attempt to add histograms::Add with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 or h2 have Sumw2 set
if (fSumw2.fN == 0 && (h1->GetSumw2N() != 0 || h2->GetSumw2N() != 0)) Sumw2();
// - Add statistics
Double_t nEntries = c1*h1->GetEntries() + c2*h2->GetEntries();
Stat_t s1[kNstat], s2[kNstat], s3[kNstat];
Int_t i;
for (i=0;i<kNstat;i++) {s1[i] = s2[i] = s3[i] = 0;}
h1->GetStats(s1);
h2->GetStats(s2);
for (i=0;i<kNstat;i++) {
if (i == 1) s3[i] = c1*c1*s1[i] + c2*c2*s2[i];
else s3[i] = c1*s1[i] + c2*s2[i];
}
PutStats(s3);
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
cu = c1*h1->GetBinContent(bin)+ c2*h2->GetBinContent(bin);
SetBinContent(bin,cu);
if (fSumw2.fN) {
Double_t error1 = h1->GetBinError(bin);
Double_t error2 = h2->GetBinError(bin);
fSumw2.fArray[bin] = c1*c1*error1*error1 + c2*c2*error2*error2;
}
}
}
}
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::AddBinContent(Int_t)
{
// -*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
AbstractMethod("AddBinContent");
}
//______________________________________________________________________________
void TH1::AddBinContent(Int_t, Stat_t)
{
// -*-*-*-*-*-*-*-*Increment bin content by a weight w*-*-*-*-*-*-*-*-*-*-*
// ===================================
AbstractMethod("AddBinContent");
}
//______________________________________________________________________________
void TH1::AddDirectory(Bool_t add)
{
// Sets the flag controlling the automatic add of histograms in memory
//
// By default (fAddDirectory = kTRUE), histograms are automatically added
// to the list of objects in memory.
// Note that one histogram can be removed from its support directory
// by calling h->SetDirectory(0) or h->SetDirectory(dir) to add it
// to the list of objects in the directory dir.
//
// NOTE that this is a static function. To call it, use;
// TH1::AddDirectory
fgAddDirectory = add;
}
//______________________________________________________________________________
Int_t TH1::BufferEmpty(Int_t action)
{
// Fill histogram with all entries in the buffer.
// action = -1 histogram is reset and refilled from the buffer (called by THistPainter::Paint)
// action = 0 histogram is filled from the buffer
// action = 1 histogram is filled and buffer is deleted
// The buffer is automatically deleted when the number of entries
// in the buffer is greater than the number of entries in the histogram
// do we need to compute the bin size?
if (!fBuffer) return 0;
Int_t nbentries = (Int_t)fBuffer[0];
if (!nbentries) return 0;
Double_t *buffer = fBuffer;
if (nbentries < 0) {
if (action == 0) return 0;
nbentries = -nbentries;
fBuffer=0;
Reset();
fBuffer = buffer;
}
if (TestBit(kCanRebin) || (fXaxis.GetXmax() <= fXaxis.GetXmin())) {
//find min, max of entries in buffer
Double_t xmin = fBuffer[2];
Double_t xmax = xmin;
for (Int_t i=1;i<nbentries;i++) {
Double_t x = fBuffer[2*i+2];
if (x < xmin) xmin = x;
if (x > xmax) xmax = x;
}
if (fXaxis.GetXmax() <= fXaxis.GetXmin()) {
THLimitsFinder::GetLimitsFinder()->FindGoodLimits(this,xmin,xmax);
} else {
fBuffer = 0;
Int_t keep = fBufferSize; fBufferSize = 0;
if (xmin < fXaxis.GetXmin()) RebinAxis(xmin,"X");
if (xmax >= fXaxis.GetXmax()) RebinAxis(xmax,"X");
fBuffer = buffer;
fBufferSize = keep;
}
}
FillN(nbentries,&fBuffer[2],&fBuffer[1],2);
if (action > 0) { delete [] fBuffer; fBuffer = 0; fBufferSize = 0;}
else {
if (nbentries == (Int_t)fEntries) fBuffer[0] = -nbentries;
else fBuffer[0] = 0;
}
return nbentries;
}
//______________________________________________________________________________
Int_t TH1::BufferFill(Axis_t x, Stat_t w)
{
// accumulate arguments in buffer. When buffer is full, empty the buffer
// fBuffer[0] = number of entries in buffer
// fBuffer[1] = w of first entry
// fBuffer[2] = x of first entry
if (!fBuffer) return -2;
Int_t nbentries = (Int_t)fBuffer[0];
if (nbentries < 0) {
nbentries = -nbentries;
fBuffer[0] = nbentries;
if (fEntries > 0) {
Double_t *buffer = fBuffer; fBuffer=0;
Reset();
fBuffer = buffer;
}
}
if (2*nbentries+2 >= fBufferSize) {
BufferEmpty(1);
return Fill(x,w);
}
fBuffer[2*nbentries+1] = w;
fBuffer[2*nbentries+2] = x;
fBuffer[0] += 1;
return -2;
}
//______________________________________________________________________________
Double_t TH1::Chi2Test(const TH1 *h, Option_t *option, Int_t constraint) const
{
//The Chi2 (Pearson's) test for differences between h and this histogram.
//a small value of prob indicates a significant difference between the distributions
//
//if the data was collected in such a way that the number of entries
//in the first histogram is necessarily equal to the number of entries
//in the second, the parameter _constraint_ must be made 1. Default is 0.
//any additional constraints on the data lower the number of degrees of freedom
//(i.e. increase constraint to more positive values) in accordance with
//their number
//
///options:
// "O" : overflows included
// "U" : underflows included
// by default underflows and overflows are not included
//
// "P" : print information about number of degrees of freedom and the value of chi2
// "Chi2" : the function returns the Chisquare instead of the probability
// "Chi2/ndf" : the function returns the Chi2/ndf
// if none of the options "Chi2" or "Chi2/ndf" is specified, the function returns
// the Pearson test, ie probability.
//
// algorithm taken from "Numerical Recipes in C++"
// implementation by Anna Kreshuk
//
// A good description of the Chi2test can be seen at:
// http://www.itl.nist.gov/div898/handbook/eda/section3/eda35f.htm
// See also TH1::KolmogorovTest (including NOTE2)
Int_t i, i_start, i_end;
TString opt = option;
opt.ToUpper();
TAxis *axis1 = this->GetXaxis();
TAxis *axis2 = h->GetXaxis();
Int_t nbins1 = axis1->GetNbins();
Int_t nbins2 = axis2->GetNbins();
//check dimensions
if (this->GetDimension()!=1 || h->GetDimension()!=1){
Error("Chi2Test","for 1-d only");
return 0;
}
//check number of channels
if (nbins1 != nbins2){
Error("Chi2Test","different number of channels");
return 0;
}
//see options
i_start = 1;
i_end = nbins1;
Int_t ndf = nbins1-constraint;
if(opt.Contains("O")) {
i_end = nbins1+1;
ndf++;
}
if(opt.Contains("U")) {
i_start = 0;
ndf++;
}
//Compute the normalisation factor
Double_t sum1=0, sum2=0;
for (i=i_start; i<=i_end; i++){
sum1 += this->GetBinContent(i);
sum2 += h->GetBinContent(i);
}
//check that the histograms are not empty
if (sum1 == 0 || sum2 == 0){
Error("Chi2Test","one of the histograms is empty");
return 0;
}
Double_t chsq = 0;
Double_t bin1, bin2, err1, err2, temp;
for (i=i_start; i<=i_end; i++){
bin1 = this->GetBinContent(i)/sum1;
bin2 = h->GetBinContent(i)/sum2;
if (bin1 ==0 && bin2==0){
--ndf; //no data means one less degree of freedom
} else {
temp = bin1-bin2;
err1=this->GetBinError(i);
err2=h->GetBinError(i);
if (err1 == 0 && err2 == 0){
Error("Chi2Test", "bins with non-zero content and zero error");
return 0;
}
err1*=err1;
err2*=err2;
err1/=sum1*sum1;
err2/=sum2*sum2;
chsq+=temp*temp/(err1+err2);
}
}
Double_t prob = TMath::Prob(0.5*chsq, Int_t(0.5*ndf));
if (opt.Contains("P")){
Printf("Chi2 = %f, Prob = %g, NDF = %d\n", chsq,prob,ndf);
}
if (opt.Contains("CHI2/NDF")){
if (ndf == 0) return 0;
return chsq/ndf;
}
if (opt.Contains("CHI2")){
return chsq;
}
return prob;
}
//______________________________________________________________________________
Double_t TH1::ComputeIntegral()
{
// Compute integral (cumulative sum of bins)
// The result stored in fIntegral is used by the GetRandom functions.
// This function is automatically called by GetRandom when the fIntegral
// array does not exist or when the number of entries in the histogram
// has changed since the previous call to GetRandom.
// The resulting integral is normalized to 1
Int_t bin, binx, biny, binz, ibin;
// delete previously computed integral (if any)
if (fIntegral) delete [] fIntegral;
// - Allocate space to store the integral and compute integral
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
Int_t nxy = nbinsx*nbinsy;
Int_t nbins = nxy*nbinsz;
fIntegral = new Double_t[nbins+2];
ibin = 0;
fIntegral[ibin] = 0;
for (binz=1;binz<=nbinsz;binz++) {
for (biny=1;biny<=nbinsy;biny++) {
for (binx=1;binx<=nbinsx;binx++) {
ibin++;
bin = GetBin(binx, biny, binz);
fIntegral[ibin] = fIntegral[ibin-1] + GetBinContent(bin);
}
}
}
// - Normalize integral to 1
if (fIntegral[nbins] == 0 ) {
Error("ComputeIntegral", "Integral = zero"); return 0;
}
for (bin=1;bin<=nbins;bin++) fIntegral[bin] /= fIntegral[nbins];
fIntegral[nbins+1] = fEntries;
return fIntegral[nbins];
}
//______________________________________________________________________________
Double_t *TH1::GetIntegral()
{
// Return a pointer to the array of bins integral.
// if the pointer fIntegral is null, TH1::ComputeIntegral is called
if (fIntegral) ComputeIntegral();
return fIntegral;
}
//______________________________________________________________________________
void TH1::Copy(TObject &obj) const
{
// -*-*-*-*-*Copy this histogram structure to newth1*-*-*-*-*-*-*-*-*-*-*-*
// =======================================
//
// Note that this function does not copy the list of associated functions.
// Use TObJect::Clone to make a full copy of an histogram.
if (((TH1&)obj).fDirectory) {
// We are likely to change the hash value of this object
// with TNamed::Copy, to keep things correct, we need to
// clean up its existing entries.
((TH1&)obj).fDirectory->GetList()->Remove(&obj);
((TH1&)obj).fDirectory = 0;
}
TNamed::Copy(obj);
((TH1&)obj).fDimension = fDimension;
((TH1&)obj).fNormFactor= fNormFactor;
((TH1&)obj).fEntries = fEntries;
((TH1&)obj).fNcells = fNcells;
((TH1&)obj).fBarOffset = fBarOffset;
((TH1&)obj).fBarWidth = fBarWidth;
((TH1&)obj).fTsumw = fTsumw;
((TH1&)obj).fTsumw2 = fTsumw2;
((TH1&)obj).fTsumwx = fTsumwx;
((TH1&)obj).fTsumwx2 = fTsumwx2;
((TH1&)obj).fMaximum = fMaximum;
((TH1&)obj).fMinimum = fMinimum;
((TH1&)obj).fOption = fOption;
((TH1&)obj).fBuffer = 0;
((TH1&)obj).fBufferSize= fBufferSize;
if (fBuffer) {
Double_t *buf = new Double_t[fBufferSize];
for (Int_t i=0;i<fBufferSize;i++) buf[i] = fBuffer[i];
((TH1&)obj).fBuffer = buf;
}
TAttLine::Copy(((TH1&)obj));
TAttFill::Copy(((TH1&)obj));
TAttMarker::Copy(((TH1&)obj));
fXaxis.Copy(((TH1&)obj).fXaxis);
fYaxis.Copy(((TH1&)obj).fYaxis);
fZaxis.Copy(((TH1&)obj).fZaxis);
((TH1&)obj).fXaxis.SetParent(&obj);
((TH1&)obj).fYaxis.SetParent(&obj);
((TH1&)obj).fZaxis.SetParent(&obj);
fContour.Copy(((TH1&)obj).fContour);
fSumw2.Copy(((TH1&)obj).fSumw2);
// fFunctions->Copy(((TH1&)obj).fFunctions);
if (fgAddDirectory && gDirectory) {
gDirectory->Append(&obj);
((TH1&)obj).fDirectory = gDirectory;
}
}
//______________________________________________________________________________
Int_t TH1::DistancetoPrimitive(Int_t px, Int_t py)
{
// -*-*-*-*-*-*-*-*-*Compute distance from point px,py to a line*-*-*-*-*-*
// ===========================================
// Compute the closest distance of approach from point px,py to elements
// of an histogram.
// The distance is computed in pixels units.
//
// Algorithm:
// Currently, this simple model computes the distance from the mouse
// to the histogram contour only.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (!fPainter) return 9999;
return fPainter->DistancetoPrimitive(px,py);
}
//______________________________________________________________________________
void TH1::Divide(TF1 *f1, Double_t c1)
{
// Performs the operation: this = this/(c1*f1)
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
//
// Only bins inside the function range are recomputed.
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Divide
if (!f1) {
Error("Add","Attempt to divide by a non-existing function");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// - Add statistics
Double_t nEntries = fEntries;
Stat_t s1[10];
Int_t i;
for (i=0;i<10;i++) {s1[i] = 0;}
PutStats(s1);
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu,w;
Double_t xx[3];
Double_t *params = 0;
f1->InitArgs(xx,params);
for (binz=0;binz<=nbinsz+1;binz++) {
xx[2] = fZaxis.GetBinCenter(binz);
for (biny=0;biny<=nbinsy+1;biny++) {
xx[1] = fYaxis.GetBinCenter(biny);
for (binx=0;binx<=nbinsx+1;binx++) {
xx[0] = fXaxis.GetBinCenter(binx);
if (!f1->IsInside(xx)) continue;
TF1::RejectPoint(kFALSE);
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
Double_t error1 = GetBinError(bin);
cu = c1*f1->EvalPar(xx);
if (TF1::RejectedPoint()) continue;
if (cu) w = GetBinContent(bin)/cu;
else w = 0;
SetBinContent(bin,w);
if (fSumw2.fN) {
if (cu != 0) fSumw2.fArray[bin] = error1*error1/(cu*cu);
else fSumw2.fArray[bin] = 0;
}
}
}
}
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Divide(const TH1 *h1)
{
// -*-*-*-*-*-*-*-*-*Divide this histogram by h1*-*-*-*-*-*-*-*-*-*-*-*-*
// ===========================
//
// this = this/h1
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
// Note that if h1 has Sumw2 set, Sumw2 is automatically called for this
// if not already set.
// The resulting errors are calculated assuming uncorrelated histograms.
// See the other TH1::Divide that gives the possibility to optionaly
// compute Binomial errors.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Scale
if (!h1) {
Error("Divide","Attempt to divide by a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()) {
Error("Divide","Attempt to divide histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Divide","Attempt to divide histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 has Sumw2 set
if (fSumw2.fN == 0 && h1->GetSumw2N() != 0) Sumw2();
// - Reset statistics
Double_t nEntries = fEntries;
fEntries = fTsumw = 0;
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t c0,c1,w;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = GetBin(binx,biny,binz);
c0 = GetBinContent(bin);
c1 = h1->GetBinContent(bin);
if (c1) w = c0/c1;
else w = 0;
SetBinContent(bin,w);
fEntries++;
if (fSumw2.fN) {
Double_t e0 = GetBinError(bin);
Double_t e1 = h1->GetBinError(bin);
Double_t c12= c1*c1;
if (!c1) { fSumw2.fArray[bin] = 0; continue;}
fSumw2.fArray[bin] = (e0*e0*c1*c1 + e1*e1*c0*c0)/(c12*c12);
}
}
}
}
Stat_t s[kNstat];
GetStats(s);
PutStats(s);
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Divide(const TH1 *h1, const TH1 *h2, Double_t c1, Double_t c2, Option_t *option)
{
// -*-*-*Replace contents of this histogram by the division of h1 by h2*-*-*
// ==============================================================
//
// this = c1*h1/(c2*h2)
//
// if errors are defined (see TH1::Sumw2), errors are also recalculated
// Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this
// if not already set.
// The resulting errors are calculated assuming uncorrelated histograms.
// However, if option ="B" is specified, Binomial errors are computed.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Divide
TString opt = option;
opt.ToLower();
Bool_t binomial = kFALSE;
if (opt.Contains("b")) binomial = kTRUE;
if (!h1 || !h2) {
Error("Divide","Attempt to divide by a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()
|| nbinsx != h2->GetNbinsX() || nbinsy != h2->GetNbinsY() || nbinsz != h2->GetNbinsZ()) {
Error("Divide","Attempt to divide histograms with different number of bins");
return;
}
if (!c2) {
Error("Divide","Coefficient of dividing histogram cannot be zero");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Divide","Attempt to divide histograms with different axis limits");
}
if (fXaxis.GetXmin() != h2->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h2->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h2->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h2->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h2->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h2->fZaxis.GetXmax()) {
Warning("Divide","Attempt to divide histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 or h2 have Sumw2 set
if (fSumw2.fN == 0 && (h1->GetSumw2N() != 0 || h2->GetSumw2N() != 0)) Sumw2();
// - Reset statistics
Double_t nEntries = fEntries;
fEntries = fTsumw = 0;
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t b1,b2,w,d1,d2;
d1 = c1*c1;
d2 = c2*c2;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
b1 = h1->GetBinContent(bin);
b2 = h2->GetBinContent(bin);
if (b2) w = c1*b1/(c2*b2);
else w = 0;
SetBinContent(bin,w);
fEntries++;
if (fSumw2.fN) {
Double_t e1 = h1->GetBinError(bin);
Double_t e2 = h2->GetBinError(bin);
Double_t b22= b2*b2*d2;
if (!b2) { fSumw2.fArray[bin] = 0; continue;}
if (binomial) {
if (b1 != b2) {
//fSumw2.fArray[bin] = TMath::Abs(w*(1-w)/(c2*b2));//this is the formula in Hbook/Hoper1
fSumw2.fArray[bin] = TMath::Abs(w*(1-w)/b2);
} else {
//in case b1=b2 use a simplification of the special algorithm
//from TGraphAsymmErrors::BayesDivide calling Efficiency, etc
Double_t too_low = 0;
Double_t too_high = 1;
Double_t integral;
Double_t a = b1+1;
Double_t x;
for (Int_t loop=0; loop<20; loop++) {
x = 0.5*(too_high + too_low);
Double_t bt = TMath::Exp(TMath::LnGamma(a+1)-TMath::LnGamma(a)+a*log(x)+log(1-x));
if (x < (a+1.0)/(a+3.0)) integral = 1 - bt*TMath::BetaCf(x,a,1)/a;
else integral = bt*TMath::BetaCf(1-x,1,a);
if (integral > 0.683) too_low = x;
else too_high = x;
}
fSumw2.fArray[bin] = (1-x)*(1-x)/4;
}
} else {
fSumw2.fArray[bin] = d1*d2*(e1*e1*b2*b2 + e2*e2*b1*b1)/(b22*b22);
}
}
}
}
}
Stat_t s[kNstat];
GetStats(s);
PutStats(s);
if (nEntries == 0) nEntries = h1->GetEntries();
if (nEntries == 0) nEntries = 1;
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Draw(Option_t *option)
{
// -*-*-*-*-*-*-*-*-*Draw this histogram with options*-*-*-*-*-*-*-*-*-*-*-*
// ================================
//
// Histograms are drawn via the THistPainter class. Each histogram has
// a pointer to its own painter (to be usable in a multithreaded program).
// The same histogram can be drawn with different options in different pads.
// When an histogram drawn in a pad is deleted, the histogram is
// automatically removed from the pad or pads where it was drawn.
// If an histogram is drawn in a pad, then filled again, the new status
// of the histogram will be automatically shown in the pad next time
// the pad is updated. One does not need to redraw the histogram.
// To draw the current version of an histogram in a pad, one can use
// h->DrawCopy();
// This makes a clone of the histogram. Once the clone is drawn, the original
// histogram may be modified or deleted without affecting the aspect of the
// clone.
// By default, TH1::Draw clears the current pad.
//
// One can use TH1::SetMaximum and TH1::SetMinimum to force a particular
// value for the maximum or the minimum scale on the plot.
//
// TH1::UseCurrentStyle can be used to change all histogram graphics
// attributes to correspond to the current selected style.
// This function must be called for each histogram.
// In case one reads and draws many histograms from a file, one can force
// the histograms to inherit automatically the current graphics style
// by calling before gROOT->ForceStyle();
//
// See THistPainter::Paint for a description of all the drawing options
// =======================
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TString opt = option;
opt.ToLower();
if (gPad) {
if (!gPad->IsEditable()) (gROOT->GetMakeDefCanvas())();
if (!opt.Contains("same")) {
//the following statement is necessary in case one attempts to draw
//a temporary histogram already in the current pad
if (TestBit(kCanDelete)) gPad->GetListOfPrimitives()->Remove(this);
gPad->Clear();
}
}
AppendPad(opt.Data());
}
//______________________________________________________________________________
TH1 *TH1::DrawCopy(Option_t *) const
{
// -*-*-*-*-*Copy this histogram and Draw in the current pad*-*-*-*-*-*-*-*
// ===============================================
//
// Once the histogram is drawn into the pad, any further modification
// using graphics input will be made on the copy of the histogram,
// and not to the original object.
//
// See Draw for the list of options
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
AbstractMethod("DrawCopy");
return 0;
}
//______________________________________________________________________________
TH1 *TH1::DrawNormalized(Option_t *option, Double_t norm) const
{
// Draw a normalized copy of this histogram.
//
// A clone of this histogram is normalized to norm and drawn with option.
// A pointer to the normalized histogram is returned.
// The contents of the histogram copy are scaled such that the new
// sum of weights (excluding under and overflow) is equal to norm.
// Note that the returned normalized histogram is not added to the list
// of histograms in the current directory in memory.
// It is the user's responsability to delete this histogram.
// The kCanDelete bit is set for the returned object. If a pad containing
// this copy is cleared, the histogram will be automatically deleted.
//
// See Draw for the list of options
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Double_t sum = GetSumOfWeights();
if (sum == 0) {
Error("DrawNormalized","Sum of weights is null. Cannot normalized histogram: %s",GetName());
return 0;
}
Bool_t addStatus = TH1::AddDirectoryStatus();
TH1::AddDirectory(kFALSE);
TH1 *h = (TH1*)Clone();
h->SetBit(kCanDelete);
h->Scale(norm/sum);
h->Draw(option);
TH1::AddDirectory(addStatus);
return h;
}
//______________________________________________________________________________
void TH1::DrawPanel()
{
// -*-*-*-*-*Display a panel with all histogram drawing options*-*-*-*-*-*
// ==================================================
//
// See class TDrawPanelHist for example
if (!fPainter) {Draw(); if (gPad) gPad->Update();}
if (fPainter) fPainter->DrawPanel();
}
//______________________________________________________________________________
void TH1::Eval(TF1 *f1, Option_t *option)
{
// -*-*-*Evaluate function f1 at the center of bins of this histogram-*-*-*-*
// ============================================================
//
// If option "R" is specified, the function is evaluated only
// for the bins included in the function range.
// If option "A" is specified, the value of the function is added to the
// existing bin contents
// If option "S" is specified, the value of the function is used to
// generate a value, distributed according to the Poisson
// distribution, with f1 as the mean.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Double_t x[3];
Int_t range,stat,add,bin,binx,biny,binz,nbinsx, nbinsy, nbinsz;
if (!f1) return;
Double_t fu;
Double_t e=0;
TString opt = option;
opt.ToLower();
if (opt.Contains("a")) add = 1;
else add = 0;
if (opt.Contains("s")) stat = 1;
else stat = 0;
if (opt.Contains("r")) range = 1;
else range = 0;
nbinsx = fXaxis.GetNbins();
nbinsy = fYaxis.GetNbins();
nbinsz = fZaxis.GetNbins();
if (!add) Reset();
for (binz=1;binz<=nbinsz;binz++) {
x[2] = fZaxis.GetBinCenter(binz);
for (biny=1;biny<=nbinsy;biny++) {
x[1] = fYaxis.GetBinCenter(biny);
for (binx=1;binx<=nbinsx;binx++) {
bin = GetBin(binx,biny,binz);
x[0] = fXaxis.GetBinCenter(binx);
if (range && !f1->IsInside(x)) continue;
fu = f1->Eval(x[0],x[1],x[2]);
if (stat) fu = gRandom->PoissonD(fu);
if (fSumw2.fN) e = fSumw2.fArray[bin];
AddBinContent(bin,fu);
if (fSumw2.fN) fSumw2.fArray[bin] = e+ TMath::Abs(fu);
}
}
}
}
//______________________________________________________________________________
void TH1::ExecuteEvent(Int_t event, Int_t px, Int_t py)
{
// -*-*-*-*-*-*-*-*-*Execute action corresponding to one event*-*-*-*
// =========================================
// This member function is called when a histogram is clicked with the locator
//
// If Left button clicked on the bin top value, then the content of this bin
// is modified according to the new position of the mouse when it is released.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (fPainter) fPainter->ExecuteEvent(event, px, py);
}
//______________________________________________________________________________
Int_t TH1::Fill(Axis_t x)
{
// -*-*-*-*-*-*-*-*Increment bin with abscissa X by 1*-*-*-*-*-*-*-*-*-*-*
// ==================================
//
// if x is less than the low-edge of the first bin, the Underflow bin is incremented
// if x is greater than the upper edge of last bin, the Overflow bin is incremented
//
// If the storage of the sum of squares of weights has been triggered,
// via the function Sumw2, then the sum of the squares of weights is incremented
// by 1 in the bin corresponding to x.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (fBuffer) return BufferFill(x,1);
Int_t bin;
fEntries++;
bin =fXaxis.FindBin(x);
AddBinContent(bin);
if (fSumw2.fN) ++fSumw2.fArray[bin];
if (bin == 0 || bin > fXaxis.GetNbins()) {
if (!fgStatOverflows) return -1;
}
++fTsumw;
++fTsumw2;
fTsumwx += x;
fTsumwx2 += x*x;
return bin;
}
//______________________________________________________________________________
Int_t TH1::Fill(Axis_t x, Stat_t w)
{
// -*-*-*-*-*-*Increment bin with abscissa X with a weight w*-*-*-*-*-*-*-*
// =============================================
//
// if x is less than the low-edge of the first bin, the Underflow bin is incremented
// if x is greater than the upper edge of last bin, the Overflow bin is incremented
//
// If the storage of the sum of squares of weights has been triggered,
// via the function Sumw2, then the sum of the squares of weights is incremented
// by w^2 in the bin corresponding to x.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (fBuffer) return BufferFill(x,w);
Int_t bin;
fEntries++;
bin =fXaxis.FindBin(x);
AddBinContent(bin, w);
if (fSumw2.fN) fSumw2.fArray[bin] += w*w;
if (bin == 0 || bin > fXaxis.GetNbins()) {
if (!fgStatOverflows) return -1;
}
Stat_t z= (w > 0 ? w : -w);
fTsumw += z;
fTsumw2 += z*z;
fTsumwx += z*x;
fTsumwx2 += z*x*x;
return bin;
}
//______________________________________________________________________________
Int_t TH1::Fill(const char *namex, Stat_t w)
{
// Increment bin with namex with a weight w
//
// if x is less than the low-edge of the first bin, the Underflow bin is incremented
// if x is greater than the upper edge of last bin, the Overflow bin is incremented
//
// If the storage of the sum of squares of weights has been triggered,
// via the function Sumw2, then the sum of the squares of weights is incremented
// by w^2 in the bin corresponding to x.
//
Int_t bin;
fEntries++;
bin =fXaxis.FindBin(namex);
AddBinContent(bin, w);
if (fSumw2.fN) fSumw2.fArray[bin] += w*w;
if (bin == 0 || bin > fXaxis.GetNbins()) return -1;
Axis_t x = fXaxis.GetBinCenter(bin);
Stat_t z= (w > 0 ? w : -w);
fTsumw += z;
fTsumw2 += z*z;
fTsumwx += z*x;
fTsumwx2 += z*x*x;
return bin;
}
//______________________________________________________________________________
void TH1::FillN(Int_t ntimes, const Axis_t *x, const Double_t *w, Int_t stride)
{
// -*-*-*-*-*-*Fill this histogram with an array x and weights w*-*-*-*-*
// =================================================
//
// ntimes: number of entries in arrays x and w (array size must be ntimes*stride)
// x: array of values to be histogrammed
// w: array of weighs
// stride: step size through arrays x and w
//
// If the storage of the sum of squares of weights has been triggered,
// via the function Sumw2, then the sum of the squares of weights is incremented
// by w[i]^2 in the bin corresponding to x[i].
// if w is NULL each entry is assumed a weight=1
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t bin,i;
fEntries += ntimes;
Double_t ww = 1;
Int_t nbins = fXaxis.GetNbins();
ntimes *= stride;
for (i=0;i<ntimes;i+=stride) {
bin =fXaxis.FindBin(x[i]);
if (w) ww = w[i];
AddBinContent(bin, ww);
if (fSumw2.fN) fSumw2.fArray[bin] += ww*ww;
if (bin == 0 || bin > nbins) {
if (!fgStatOverflows) continue;
}
Stat_t z= (ww > 0 ? ww : -ww);
fTsumw += z;
fTsumw2 += z*z;
fTsumwx += z*x[i];
fTsumwx2 += z*x[i]*x[i];
}
}
//______________________________________________________________________________
void TH1::FillRandom(const char *fname, Int_t ntimes)
{
// -*-*-*-*-*Fill histogram following distribution in function fname*-*-*-*
// =======================================================
//
// The distribution contained in the function fname (TF1) is integrated
// over the channel contents.
// It is normalized to 1.
// Getting one random number implies:
// - Generating a random number between 0 and 1 (say r1)
// - Look in which bin in the normalized integral r1 corresponds to
// - Fill histogram channel
// ntimes random numbers are generated
//
// One can also call TF1::GetRandom to get a random variate from a function.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-**-*-*-*-*-*-*-*
Int_t bin, binx, ibin, loop;
Double_t r1, x, xv[1];
// - Search for fname in the list of ROOT defined functions
TF1 *f1 = (TF1*)gROOT->GetFunction(fname);
if (!f1) { Error("FillRandom", "Unknown function: %s",fname); return; }
// - Allocate temporary space to store the integral and compute integral
Int_t nbinsx = GetNbinsX();
Double_t *integral = new Double_t[nbinsx+1];
ibin = 0;
integral[ibin] = 0;
for (binx=1;binx<=nbinsx;binx++) {
xv[0] = fXaxis.GetBinCenter(binx);
ibin++;
Double_t fval = f1->Eval(xv[0]);
integral[ibin] = integral[ibin-1] + TMath::Abs(fval)*fXaxis.GetBinWidth(binx);
}
// - Normalize integral to 1
if (integral[nbinsx] == 0 ) {
Error("FillRandom", "Integral = zero"); return;
}
for (bin=1;bin<=nbinsx;bin++) integral[bin] /= integral[nbinsx];
// --------------Start main loop ntimes
for (loop=0;loop<ntimes;loop++) {
r1 = gRandom->Rndm(loop);
ibin = TMath::BinarySearch(nbinsx,&integral[0],r1);
binx = 1 + ibin;
//x = fXaxis.GetBinCenter(binx); //this is not OK when SetBuffer is used
x = fXaxis.GetBinLowEdge(ibin+1)
+fXaxis.GetBinWidth(ibin+1)*(r1-integral[ibin])/(integral[ibin+1] - integral[ibin]);
Fill(x, 1.);
}
delete [] integral;
}
//______________________________________________________________________________
void TH1::FillRandom(TH1 *h, Int_t ntimes)
{
// -*-*-*-*-*Fill histogram following distribution in histogram h*-*-*-*
// ====================================================
//
// The distribution contained in the histogram h (TH1) is integrated
// over the channel contents.
// It is normalized to 1.
// Getting one random number implies:
// - Generating a random number between 0 and 1 (say r1)
// - Look in which bin in the normalized integral r1 corresponds to
// - Fill histogram channel
// ntimes random numbers are generated
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-**-*-*-*-*-*-*-*
if (!h) { Error("FillRandom", "Null histogram"); return; }
if (fDimension != h->GetDimension()) {
Error("FillRandom", "Histograms with different dimensions"); return;
}
if (h->ComputeIntegral() == 0) return;
Int_t loop;
Axis_t x;
for (loop=0;loop<ntimes;loop++) {
x = h->GetRandom();
Fill(x);
}
}
//______________________________________________________________________________
Int_t TH1::FindBin(Axis_t x, Axis_t y, Axis_t z)
{
// -*-*-*-*Return Global bin number corresponding to x,y,z*-*-*-*-*-*-*
// ===============================================
//
// 2-D and 3-D histograms are represented with a one dimensional
// structure.
// This has the advantage that all existing functions, such as
// GetBinContent, GetBinError, GetBinFunction work for all dimensions.
// See also TH1::GetBin
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (GetDimension() < 2) {
return fXaxis.FindBin(x);
}
if (GetDimension() < 3) {
Int_t nx = fXaxis.GetNbins()+2;
Int_t binx = fXaxis.FindBin(x);
Int_t biny = fYaxis.FindBin(y);
return binx + nx*biny;
}
if (GetDimension() < 4) {
Int_t nx = fXaxis.GetNbins()+2;
Int_t ny = fYaxis.GetNbins()+2;
Int_t binx = fXaxis.FindBin(x);
Int_t biny = fYaxis.FindBin(y);
Int_t binz = fZaxis.FindBin(z);
return binx + nx*(biny +ny*binz);
}
return -1;
}
//______________________________________________________________________________
TObject *TH1::FindObject(const char *name) const
{
// search object named name in the list of functions
if (fFunctions) return fFunctions->FindObject(name);
return 0;
}
//______________________________________________________________________________
TObject *TH1::FindObject(const TObject *obj) const
{
// search object obj in the list of functions
if (fFunctions) return fFunctions->FindObject(obj);
return 0;
}
//______________________________________________________________________________
Int_t TH1::Fit(const char *fname ,Option_t *option ,Option_t *goption, Axis_t xxmin, Axis_t xxmax)
{
// Fit histogram with function fname
// =================================
// fname is the name of an already predefined function created by TF1 or TF2
// Predefined functions such as gaus, expo and poln are automatically
// created by ROOT.
// fname can also be a formula, accepted by the linear fitter (linear parts divided
// by "++" sign), for example "x++sin(x)" for fitting "[0]*x+[1]*sin(x)"
//
// This function finds a pointer to the TF1 object with name fname
// and calls TH1::Fit(TF1 *f1,...)
char *linear;
linear= (char*)strstr(fname, "++");
TF1 *f1=0;
TF2 *f2=0;
TF3 *f3=0;
Int_t ndim=GetDimension();
if (linear){
if (ndim<2){
f1=new TF1(fname, fname, xxmin, xxmax);
return Fit(f1,option,goption,xxmin,xxmax);
}
else if (ndim<3){
f2=new TF2(fname, fname);
return Fit(f2,option,goption,xxmin,xxmax);
}
else{
f3=new TF3(fname, fname);
return Fit(f3,option,goption,xxmin,xxmax);
}
}
else{
f1 = (TF1*)gROOT->GetFunction(fname);
if (!f1) { Printf("Unknown function: %s",fname); return -1; }
return Fit(f1,option,goption,xxmin,xxmax);
}
}
//______________________________________________________________________________
Int_t TH1::Fit(TF1 *f1 ,Option_t *option ,Option_t *goption, Axis_t xxmin, Axis_t xxmax)
{
// Fit histogram with function f1
// ==============================
//
// Fit this histogram with function f1.
//
// The list of fit options is given in parameter option.
// option = "W" Set all errors to 1
// = "I" Use integral of function in bin instead of value at bin center
// = "L" Use Loglikelihood method (default is chisquare method)
// = "LL" Use Loglikelihood method and bin contents are not integers)
// = "U" Use a User specified fitting algorithm (via SetFCN)
// = "Q" Quiet mode (minimum printing)
// = "V" Verbose mode (default is between Q and V)
// = "E" Perform better Errors estimation using Minos technique
// = "B" Use this option when you want to fix one or more parameters
// and the fitting function is like "gaus","expo","poln","landau".
// = "M" More. Improve fit results
// = "R" Use the Range specified in the function range
// = "N" Do not store the graphics function, do not draw
// = "0" Do not plot the result of the fit. By default the fitted function
// is drawn unless the option"N" above is specified.
// = "+" Add this new fitted function to the list of fitted functions
// (by default, any previous function is deleted)
// = "C" In case of linear fitting, don't calculate the chisquare
// (saves time)
// = "F" If fitting a polN, switch to minuit fitter
//
// When the fit is drawn (by default), the parameter goption may be used
// to specify a list of graphics options. See TH1::Draw for a complete
// list of these options.
//
// In order to use the Range option, one must first create a function
// with the expression to be fitted. For example, if your histogram
// has a defined range between -4 and 4 and you want to fit a gaussian
// only in the interval 1 to 3, you can do:
// TF1 *f1 = new TF1("f1","gaus",1,3);
// histo->Fit("f1","R");
//
// Setting initial conditions
// ==========================
// Parameters must be initialized before invoking the Fit function.
// The setting of the parameter initial values is automatic for the
// predefined functions : poln, expo, gaus, landau. One can however disable
// this automatic computation by specifying the option "B".
// Note that if a predefined function is defined with an argument,
// eg, gaus(0), expo(1), you must specify the initial values for
// the parameters.
// You can specify boundary limits for some or all parameters via
// f1->SetParLimits(p_number, parmin, parmax);
// if parmin>=parmax, the parameter is fixed
// Note that you are not forced to fix the limits for all parameters.
// For example, if you fit a function with 6 parameters, you can do:
// func->SetParameters(0,3.1,1.e-6,-8,0,100);
// func->SetParLimits(3,-10,-4);
// func->FixParameter(4,0);
// func->SetParLimits(5, 1,1);
// With this setup, parameters 0->2 can vary freely
// Parameter 3 has boundaries [-10,-4] with initial value -8
// Parameter 4 is fixed to 0
// Parameter 5 is fixed to 100.
// When the lower limit and upper limit are equal, the parameter is fixed.
// However to fix a parameter to 0, one must call the FixParameter function.
//
// Note that option "I" gives better results but is slower.
//
//
// Changing the fitting function
// =============================
// By default the fitting function H1FitChisquare is used.
// To specify a User defined fitting function, specify option "U" and
// call the following functions:
// TVirtualFitter::Fitter(myhist)->SetFCN(MyFittingFunction)
// where MyFittingFunction is of type:
// extern void MyFittingFunction(Int_t &npar, Double_t *gin, Double_t &f, Double_t *u, Int_t flag);
//
// Associated functions
// ====================
// One or more object (typically a TF1*) can be added to the list
// of functions (fFunctions) associated to each histogram.
// When TH1::Fit is invoked, the fitted function is added to this list.
// Given an histogram h, one can retrieve an associated function
// with: TF1 *myfunc = h->GetFunction("myfunc");
//
// Access to the fit results
// =========================
// If the histogram is made persistent, the list of
// associated functions is also persistent. Given a pointer (see above)
// to an associated function myfunc, one can retrieve the function/fit
// parameters with calls such as:
// Double_t chi2 = myfunc->GetChisquare();
// Double_t par0 = myfunc->GetParameter(0); //value of 1st parameter
// Double_t err0 = myfunc->GetParError(0); //error on first parameter
//
// Access to the fit covariance matrix
// ===================================
// Example1:
// TH1F h("h","test",100,-2,2);
// h.FillRandom("gaus",1000);
// h.Fit("gaus");
// Double_t matrix[3][3];
// gMinuit->mnemat(&matrix[0][0],3);
// Example2:
// TH1F h("h","test",100,-2,2);
// h.FillRandom("gaus",1000);
// h.Fit("gaus");
// TVirtualFitter *fitter = TVirtualFitter::GetFitter();
// TMatrixD matrix(npar,npar,fitter->GetCovarianceMatrix());
// Double_t errorFirstPar = fitter->GetCovarianceMatrixElement(0,0);
//
//
// Changing the maximum number of parameters
// =========================================
// By default, the fitter TMinuit is initialized with a maximum of 25 parameters.
// You can redefine this default value by calling :
// TVirtualFitter::Fitter(0,150); //to get a maximum of 150 parameters
//
// Excluding points
// ================
// Use TF1::RejectPoint inside your fitting function to exclude points
// within a certain range from the fit. Example:
// Double_t fline(Double_t *x, Double_t *par)
// {
// if (x[0] > 2.5 && x[0] < 3.5) {
// TF1::RejectPoint();
// return 0;
// }
// return par[0] + par[1]*x[0];
// }
//
// void exclude() {
// TF1 *f1 = new TF1("f1","[0] +[1]*x +gaus(2)",0,5);
// f1->SetParameters(6,-1,5,3,0.2);
// TH1F *h = new TH1F("h","background + signal",100,0,5);
// h->FillRandom("f1",2000);
// TF1 *fline = new TF1("fline",fline,0,5,2);
// fline->SetParameters(2,-1);
// h->Fit("fline","l");
// }
//
// Warning when using the option "0"
// =================================
// When selecting the option "0", the fitted function is added to
// the list of functions of the histogram, but it is not drawn.
// You can undo what you disabled in the following way:
// h.Fit("myFunction","0"); // fit, store function but do not draw
// h.Draw(); function is not drawn
// const Int_t kNotDraw = 1<<9;
// h.GetFunction("myFunction")->ResetBit(kNotDraw);
// h.Draw(); // function is visible again
//
// Access to the Fitter information during fitting
// ===============================================
// This function calls only the abstract fitter TVirtualFitter.
// The default fitter is TFitter (calls TMinuit).
// The default fitter can be set in the resource file in etc/system.rootrc
// Root.Fitter: Fumili
// A different fitter can also be set via TVirtualFitter::SetDefaultFitter.
// For example, to call the "Fumili" fitter instead of "Minuit", do
// TVirtualFitter::SetDefaultFitter("Fumili");
// During the fitting process, the objective function:
// chisquare, likelihood or any user defined algorithm
// is called (see eg in the TFitter class, the static functions
// H1FitChisquare, H1FitLikelihood).
// This objective function, in turn, calls the user theoretical function.
// This user function is a static function called from the TF1 *f1 function.
// Inside this user defined theoretical function , one can access:
// TVirtualFitter *fitter = TVirtualFitter::GetFitter(); //the current fitter
// TH1 *hist = (TH1*)fitter->GetObjectFit(); //the histogram being fitted
// TF1 +f1 = (TF1*)fitter->GetUserFunction(); //the user theoretical function
//
// By default, the fitter TMinuit is initialized with a maximum of 25 parameters.
// For fitting linear functions (containing the "++" sign" and polN functions,
// the linear fitter is initialized.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t fitResult = 0;
Int_t i, npar,nvpar,nparx;
Double_t par, we, al, bl;
Double_t eplus,eminus,eparab,globcc,amin,aminref,edm,errdef,werr;
Double_t params[100], arglist[100];
Axis_t xmin, xmax, ymin, ymax, zmin, zmax, binwidx, binwidy, binwidz;
Int_t hxfirst, hxlast, hyfirst, hylast, hzfirst, hzlast;
TF1 *fnew1;
TF2 *fnew2;
TF3 *fnew3;
// Check validity of function
if (!f1) {
Error("Fit", "function may not be null pointer");
return 0;
}
if (f1->IsZombie()) {
Error("Fit", "function is zombie");
return 0;
}
npar = f1->GetNpar();
if (npar <= 0) {
Error("Fit", "function %s has illegal number of parameters = %d", f1->GetName(), npar);
return 0;
}
// Check that function has same dimension as histogram
if (f1->GetNdim() != GetDimension()) {
Error("Fit","function %s dimension, %d, does not match histogram dimension, %d",
f1->GetName(), f1->GetNdim(), GetDimension());
return 0;
}
hxfirst = fXaxis.GetFirst();
hxlast = fXaxis.GetLast();
binwidx = fXaxis.GetBinWidth(hxlast);
xmin = fXaxis.GetBinLowEdge(hxfirst);
xmax = fXaxis.GetBinLowEdge(hxlast) +binwidx;
hyfirst = fYaxis.GetFirst();
hylast = fYaxis.GetLast();
binwidy = fYaxis.GetBinWidth(hylast);
ymin = fYaxis.GetBinLowEdge(hyfirst);
ymax = fYaxis.GetBinLowEdge(hylast) +binwidy;
hzfirst = fZaxis.GetFirst();
hzlast = fZaxis.GetLast();
binwidz = fZaxis.GetBinWidth(hzlast);
zmin = fZaxis.GetBinLowEdge(hzfirst);
zmax = fZaxis.GetBinLowEdge(hzlast) +binwidz;
// - Decode list of options into fitOption
Foption_t fitOption;
if (!FitOptionsMake(option,fitOption)) return 0;
if (xxmin != xxmax) {
f1->SetRange(xxmin,ymin,zmin,xxmax,ymax,zmax);
fitOption.Range = 1;
}
// - Check if Minuit is initialized and create special functions
Int_t special = f1->GetNumber();
Bool_t linear = f1->IsLinear();
if (special==299+npar)
linear = kTRUE;
if (fitOption.Bound || fitOption.Like || fitOption.Errors || fitOption.Gradient || fitOption.More || fitOption.User|| fitOption.Integral || fitOption.Minuit)
linear = kFALSE;
char l[] ="TLinearFitter";
Int_t strdiff = 0;
Bool_t isSet = kFALSE;
if (TVirtualFitter::GetFitter()){
//Is a fitter already set? Is it linear?
isSet=kTRUE;
strdiff = strcmp(TVirtualFitter::GetFitter()->IsA()->GetName(), l);
}
if (linear){
//
TClass *cl = gROOT->GetClass("TLinearFitter");
if (isSet && strdiff!=0) {
delete TVirtualFitter::GetFitter();
isSet=kFALSE;
}
if (!isSet) {
TVirtualFitter::SetFitter((TVirtualFitter *)cl->New());
}
} else {
if (isSet && strdiff==0){
delete TVirtualFitter::GetFitter();
isSet=kFALSE;
}
if (!isSet)
TVirtualFitter::SetFitter(0);
}
TVirtualFitter *hFitter = TVirtualFitter::Fitter(this, f1->GetNpar());
hFitter->Clear();
// - Get pointer to the function by searching in the list of functions in ROOT
gF1 = f1;
hFitter->SetUserFunc(f1);
if (xxmin != xxmax) f1->SetRange(xxmin,ymin,zmin,xxmax,ymax,zmax);
hFitter->SetFitOption(fitOption);
// - Is a Fit range specified?
Double_t fxmin, fymin, fzmin, fxmax, fymax, fzmax;
if (fitOption.Range) {
f1->GetRange(fxmin, fymin, fzmin, fxmax, fymax, fzmax);
if (fxmin > xmin) xmin = fxmin;
if (fymin > ymin) ymin = fymin;
if (fzmin > zmin) zmin = fzmin;
if (fxmax < xmax) xmax = fxmax;
if (fymax < ymax) ymax = fymax;
if (fzmax < zmax) zmax = fzmax;
hxfirst = fXaxis.FindFixBin(xmin); if (hxfirst < 1) hxfirst = 1;
hxlast = fXaxis.FindFixBin(xmax); if (hxlast > fXaxis.GetLast()) hxlast = fXaxis.GetLast();
hyfirst = fYaxis.FindFixBin(ymin); if (hyfirst < 1) hyfirst = 1;
hylast = fYaxis.FindFixBin(ymax); if (hylast > fYaxis.GetLast()) hylast = fYaxis.GetLast();
hzfirst = fZaxis.FindFixBin(zmin); if (hzfirst < 1) hzfirst = 1;
hzlast = fZaxis.FindFixBin(zmax); if (hzlast > fZaxis.GetLast()) hzlast = fZaxis.GetLast();
} else {
f1->SetRange(xmin,ymin,zmin,xmax,ymax,zmax);
}
hFitter->SetXfirst(hxfirst); hFitter->SetXlast(hxlast);
hFitter->SetYfirst(hyfirst); hFitter->SetYlast(hylast);
hFitter->SetZfirst(hzfirst); hFitter->SetZlast(hzlast);
if (linear){
hFitter->ExecuteCommand("FitHist", 0, 0);
} else {
// - If case of a predefined function, then compute initial values of parameters
if (fitOption.Bound) special = 0;
if (special == 100) H1InitGaus();
else if (special == 400) H1InitGaus();
else if (special == 200) H1InitExpo();
else if (special == 299+npar) H1InitPolynom();
// - Some initialisations
if (!fitOption.Verbose) {
arglist[0] = -1;
hFitter->ExecuteCommand("SET PRINT", arglist,1);
arglist[0] = 0;
hFitter->ExecuteCommand("SET NOW", arglist,0);
}
// - Set error criterion for chisquare or likelihood methods
// - MINUIT ErrDEF should not be set to 0.5 in case of loglikelihood fit.
// - because the FCN is already multiplied by 2 in H1FitLikelihood
// - if Hoption.User is specified, assume that the user has already set
// - his minimization function via SetFCN.
arglist[0] = TVirtualFitter::GetErrorDef();
if (fitOption.Like) {
hFitter->SetFitMethod("H1FitLikelihood");
} else {
if (!fitOption.User) hFitter->SetFitMethod("H1FitChisquare");
}
hFitter->ExecuteCommand("SET Err",arglist,1);
// - Transfer names and initial values of parameters to Minuit
Int_t nfixed = 0;
for (i=0;i<npar;i++) {
par = f1->GetParameter(i);
f1->GetParLimits(i,al,bl);
if (al*bl != 0 && al >= bl) {
al = bl = 0;
arglist[nfixed] = i+1;
nfixed++;
}
we = 0.1*TMath::Abs(bl-al);
if (we == 0) we = 0.3*TMath::Abs(par);
if (we == 0) we = binwidx;
hFitter->SetParameter(i,f1->GetParName(i),par,we,al,bl);
}
if(nfixed > 0)hFitter->ExecuteCommand("FIX",arglist,nfixed); // Otto
// - Set Gradient
if (fitOption.Gradient) {
if (fitOption.Gradient == 1) arglist[0] = 1;
else arglist[0] = 0;
hFitter->ExecuteCommand("SET GRAD",arglist,1);
}
// - Reset Print level
if (fitOption.Verbose) {
arglist[0] = 0; hFitter->ExecuteCommand("SET PRINT", arglist,1);
}
// - Compute sum of squares of errors in the bin range
Double_t ey, sumw2=0;
for (i=hxfirst;i<=hxlast;i++) {
ey = GetBinError(i);
sumw2 += ey*ey;
}
//
//
// printf("h1: sumw2=%f\n", sumw2);
//
// - Perform minimization
arglist[0] = TVirtualFitter::GetMaxIterations();
arglist[1] = sumw2*TVirtualFitter::GetPrecision();
fitResult = hFitter->ExecuteCommand("MIGRAD",arglist,2);
if (fitResult != 0) {
// Abnormal termination, MIGRAD might not have converged on a
// minimum.
if (!fitOption.Quiet) {
Warning("Fit","Abnormal termination of minimization.");
}
}
if (fitOption.More) {
hFitter->ExecuteCommand("IMPROVE",arglist,0);
}
if (fitOption.Errors) {
hFitter->ExecuteCommand("HESSE",arglist,0);
hFitter->ExecuteCommand("MINOS",arglist,0);
}
// - Get return status
char parName[50];
for (i=0;i<npar;i++) {
hFitter->GetParameter(i,parName, par,we,al,bl);
if (!fitOption.Errors) werr = we;
else {
hFitter->GetErrors(i,eplus,eminus,eparab,globcc);
if (eplus > 0 && eminus < 0) werr = 0.5*(eplus-eminus);
else werr = we;
}
params[i] = par;
f1->SetParameter(i,par);
f1->SetParError(i,werr);
}
hFitter->GetStats(aminref,edm,errdef,nvpar,nparx);
// If Log Likelihood, compute an equivalent chisquare
//if (fitOption.Like) amin = hFitter->Chisquare(npar, params, amin, params, 1);
amin = aminref;
if (fitOption.Like) amin = hFitter->Chisquare(npar, params);
f1->SetChisquare(amin);
f1->SetNDF(f1->GetNumberFitPoints()-npar+nfixed);
}
// - Print final values of parameters.
if (!fitOption.Quiet) {
if (fitOption.Errors) hFitter->PrintResults(4,aminref);
else hFitter->PrintResults(3,aminref);
}
// - Store fitted function in histogram functions list and draw
if (!fitOption.Nostore) {
if (!fitOption.Plus) {
TIter next(fFunctions, kIterBackward);
TObject *obj;
while ((obj = next())) {
if (obj->InheritsFrom(TF1::Class())) {
fFunctions->Remove(obj);
delete obj;
}
}
}
if (GetDimension() < 2) {
fnew1 = new TF1();
f1->Copy(*fnew1);
fFunctions->Add(fnew1);
fnew1->SetParent(this);
fnew1->Save(xmin,xmax,0,0,0,0);
if (fitOption.Nograph) fnew1->SetBit(TF1::kNotDraw);
fnew1->SetBit(TFormula::kNotGlobal);
} else if (GetDimension() < 3) {
fnew2 = new TF2();
f1->Copy(*fnew2);
fFunctions->Add(fnew2);
fnew2->SetParent(this);
fnew2->Save(xmin,xmax,ymin,ymax,0,0);
if (fitOption.Nograph) fnew2->SetBit(TF1::kNotDraw);
fnew2->SetBit(TFormula::kNotGlobal);
} else {
fnew3 = new TF3();
f1->Copy(*fnew3);
fFunctions->Add(fnew3);
fnew3->SetParent(this);
fnew3->SetBit(TFormula::kNotGlobal);
}
if (TestBit(kCanDelete)) return fitResult;
if (!fitOption.Nograph && GetDimension() < 3) Draw(goption);
}
return fitResult;
}
//______________________________________________________________________________
void TH1::FitPanel()
{
// -*-*-*-*-*Display a panel with all histogram fit options*-*-*-*-*-*
// ==============================================
//
// See class TFitPanel for example
if (fPainter) fPainter->FitPanel();
}
//______________________________________________________________________________
TH1 *TH1::GetAsymmetry(TH1* h2, Double_t c2, Double_t dc2)
{
// return an histogram containing the asymmetry of this histogram with h2,
// where the asymmetry is defined as:
//
// Asymmetry = (h1 - h2)/(h1 + h2) where h1 = this
//
// works for 1D, 2D, etc. histograms
// c2 is an optional argument that gives a relative weight between the two
// histograms, and dc2 is the error on this weight. This is useful, for example,
// when forming an asymmetry between two histograms from 2 different data sets that
// need to be normalized to each other in some way. The function calculates
// the errors asumming Poisson statistics on h1 and h2 (that is, dh = sqrt(h)).
//
// example: assuming 'h1' and 'h2' are already filled
//
// h3 = h1->GetAsymmetry(h2)
//
// then 'h3' is created and filled with the asymmetry between 'h1' and 'h2';
// h1 and h2 are left intact.
//
// Note that it is the user's responsibility to manage the created histogram.
//
// code proposed by Jason Seely (seely@mit.edu) and adapted by R.Brun
//
// clone the histograms so top and bottom will have the
// correct dimensions:
// Sumw2 just makes sure the errors will be computed properly
// when we form sums and ratios below.
Bool_t addStatus = TH1::AddDirectoryStatus();
TH1::AddDirectory(kFALSE);
TH1 *asym = (TH1*)Clone();
asym->Sumw2();
TH1 *top = (TH1*)asym->Clone();
TH1 *bottom = (TH1*)asym->Clone();
TH1::AddDirectory(addStatus);
// form the top and bottom of the asymmetry, and then divide:
TH1 *h1 = this;
top->Add(h1,h2,1,-c2);
bottom->Add(h1,h2,1,c2);
asym->Divide(top,bottom);
Int_t xmax = asym->GetNbinsX();
Int_t ymax = asym->GetNbinsY();
Int_t zmax = asym->GetNbinsZ();
Double_t bot, error, a, b, da, db;
// now loop over bins to calculate the correct errors
// the reason this error calculation looks complex is because of c2
for(Int_t i=1; i<= xmax; i++){
for(Int_t j=1; j<= ymax; j++){
for(Int_t k=1; k<= zmax; k++){
// here some bin contents are written into variables to make the error
// calculation a little more legible:
a = h1->GetBinContent(i,j,k);
b = h2->GetBinContent(i,j,k);
bot = bottom->GetBinContent(i,j,k);
// make sure there are some events, if not, then the errors are set = 0
// automatically.
if(bot < 1){}
else{
// computation of errors by Christos Leonidopoulos
da = h1->GetBinError(i,j,k);
db = h2->GetBinError(i,j,k);
error = 2*TMath::Sqrt(a*a*c2*c2*db*db + c2*c2*b*b*da*da+a*a*b*b*dc2*dc2)/(bot*bot);
asym->SetBinError(i,j,k,error);
}
}
}
}
delete top;
delete bottom;
return asym;
}
//______________________________________________________________________________
Int_t TH1::GetDefaultBufferSize()
{
// return the default buffer size for automatic histograms
// the parameter fgBufferSize may be changed via SetDefaultBufferSize
return fgBufferSize;
}
//______________________________________________________________________________
Double_t TH1::GetEntries() const
{
// return the current number of entries
if (fBuffer) ((TH1*)this)->BufferEmpty();
return fEntries;
}
//______________________________________________________________________________
char *TH1::GetObjectInfo(Int_t px, Int_t py) const
{
// Redefines TObject::GetObjectInfo.
// Displays the histogram info (bin number, contents, integral up to bin
// corresponding to cursor position px,py
//
return ((TH1*)this)->GetPainter()->GetObjectInfo(px,py);
}
//______________________________________________________________________________
TVirtualHistPainter *TH1::GetPainter()
{
// return pointer to painter
// if painter does not exist, it is created
if (!fPainter) fPainter = TVirtualHistPainter::HistPainter(this);
return fPainter;
}
//______________________________________________________________________________
Int_t TH1::GetQuantiles(Int_t nprobSum, Double_t *q, const Double_t *probSum)
{
// Compute Quantiles for this histogram
// Quantile x_q of a probability distribution Function F is defined as
//
// F(x_q) = q with 0 <= q <= 1.
//
// For instance the median x_0.5 of a distribution is defined as that value
// of the random variable for which the distribution function equals 0.5:
//
// F(x_0.5) = Probability(x < x_0.5) = 0.5
//
// code from Eddy Offermann, Renaissance
//
// input parameters
// - this 1-d histogram (TH1F,D,etc). Could also be a TProfile
// - nprobSum maximum size of array q and size of array probSum (if given)
// - probSum array of positions where quantiles will be computed.
// if probSum is null, probSum will be computed internally and will
// have a size = number of bins + 1 in h. it will correspond to the
// quantiles calculated at the lowest edge of the histogram (quantile=0) and
// all the upper edges of the bins.
// if probSum is not null, it is assumed to contain at least nprobSum values.
// output
// - return value nq (<=nprobSum) with the number of quantiles computed
// - array q filled with nq quantiles
//
// Note that the Integral of the histogram is automatically recomputed
// if the number of entries is different of the number of entries when
// the integral was computed last time. In case you do not use the Fill
// functions to fill your histogram, but SetBinContent, you must call
// TH1::ComputeIntegral before calling this function.
//
// Getting quantiles q from two histograms and storing results in a TGraph,
// a so-called QQ-plot
//
// TGraph *gr = new TGraph(nprob);
// h1->GetQuantiles(nprob,gr->GetX());
// h2->GetQuantiles(nprob,gr->GetY());
// gr->Draw("alp");
//
// Example:
// void quantiles() {
// // demo for quantiles
// const Int_t nq = 20;
// TH1F *h = new TH1F("h","demo quantiles",100,-3,3);
// h->FillRandom("gaus",5000);
//
// Double_t xq[nq]; // position where to compute the quantiles in [0,1]
// Double_t yq[nq]; // array to contain the quantiles
// for (Int_t i=0;i<nq;i++) xq[i] = Float_t(i+1)/nq;
// h->GetQuantiles(nq,yq,xq);
//
// //show the original histogram in the top pad
// TCanvas *c1 = new TCanvas("c1","demo quantiles",10,10,700,900);
// c1->Divide(1,2);
// c1->cd(1);
// h->Draw();
//
// // show the quantiles in the bottom pad
// c1->cd(2);
// gPad->SetGrid();
// TGraph *gr = new TGraph(nq,xq,yq);
// gr->SetMarkerStyle(21);
// gr->Draw("alp");
// }
if (GetDimension() > 1) {
Error("GetQuantiles","Only available for 1-d histograms");
return 0;
}
const Int_t nbins = GetXaxis()->GetNbins();
if (!fIntegral) ComputeIntegral();
if (fIntegral && fIntegral[nbins+1] != fEntries) ComputeIntegral();
Int_t i, ibin;
Double_t *prob = (Double_t*)probSum;
Int_t nq = nprobSum;
if (probSum == 0) {
nq = nbins+1;
prob = new Double_t[nq];
prob[0] = 0;
for (i=1;i<nq;i++) {
prob[i] = fIntegral[i]/fIntegral[nbins];
}
}
for (i = 0; i < nq; i++) {
ibin = TMath::BinarySearch(nbins,fIntegral,prob[i]);
while (ibin < nbins-1 && fIntegral[ibin+1] == prob[i]) {
if (fIntegral[ibin+2] == prob[i]) ibin++;
else break;
}
q[i] = GetBinLowEdge(ibin+1);
const Double_t dint = fIntegral[ibin+1]-fIntegral[ibin];
if (dint > 0) q[i] += GetBinWidth(ibin+1)*(prob[i]-fIntegral[ibin])/dint;
}
if (!probSum) delete [] prob;
return nq;
}
//______________________________________________________________________________
Int_t TH1::FitOptionsMake(Option_t *choptin, Foption_t &fitOption)
{
// -*-*-*-*-*-*-*Decode string choptin and fill fitOption structure*-*-*-*-*-*
// ================================================
Int_t nch = strlen(choptin);
if (!nch) return 1;
char chopt[32];
strcpy(chopt,choptin);
for (Int_t i=0;i<nch;i++) chopt[i] = toupper(choptin[i]);
if (strstr(chopt,"Q")) fitOption.Quiet = 1;
if (strstr(chopt,"V")) {fitOption.Verbose = 1; fitOption.Quiet = 0;}
if (strstr(chopt,"L")) fitOption.Like = 1;
if (strstr(chopt,"LL")) fitOption.Like = 2;
if (strstr(chopt,"W")) fitOption.W1 = 1;
if (strstr(chopt,"E")) fitOption.Errors = 1;
if (strstr(chopt,"M")) fitOption.More = 1;
if (strstr(chopt,"R")) fitOption.Range = 1;
if (strstr(chopt,"G")) fitOption.Gradient= 1;
if (strstr(chopt,"N")) fitOption.Nostore = 1;
if (strstr(chopt,"0")) fitOption.Nograph = 1;
if (strstr(chopt,"+")) fitOption.Plus = 1;
if (strstr(chopt,"I")) fitOption.Integral= 1;
if (strstr(chopt,"B")) fitOption.Bound = 1;
if (strstr(chopt,"U")) {fitOption.User = 1; fitOption.Like = 0;}
if (strstr(chopt,"F")) fitOption.Minuit = 1;
if (strstr(chopt,"C")) fitOption.Nochisq = 1;
return 1;
}
//______________________________________________________________________________
void H1InitGaus()
{
// -*-*-*-*Compute Initial values of parameters for a gaussian*-*-*-*-*-*-*
// ===================================================
Double_t allcha, sumx, sumx2, x, val, rms, mean;
Int_t bin;
const Double_t sqrtpi = 2.506628;
// - Compute mean value and RMS of the histogram in the given range
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
TH1 *curHist = (TH1*)hFitter->GetObjectFit();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
Double_t valmax = curHist->GetBinContent(hxfirst);
Double_t binwidx = curHist->GetBinWidth(hxfirst);
allcha = sumx = sumx2 = 0;
for (bin=hxfirst;bin<=hxlast;bin++) {
x = curHist->GetBinCenter(bin);
val = TMath::Abs(curHist->GetBinContent(bin));
if (val > valmax) valmax = val;
sumx += val*x;
sumx2 += val*x*x;
allcha += val;
}
if (allcha == 0) return;
mean = sumx/allcha;
rms = TMath::Sqrt(sumx2/allcha - mean*mean);
if (rms == 0) rms = binwidx*(hxlast-hxfirst+1)/4;
//if the distribution is really gaussian, the best approximation
//is binwidx*allcha/(sqrtpi*rms)
//However, in case of non-gaussian tails, this underestimates
//the normalisation constant. In this case the maximum value
//is a better approximation.
//We take the average of both quantities
Double_t constant = 0.5*(valmax+binwidx*allcha/(sqrtpi*rms));
//In case the mean value is outside the histo limits and
//the RMS is bigger than the range, we take
// mean = center of bins
// rms = half range
Axis_t xmin = curHist->GetXaxis()->GetXmin();
Axis_t xmax = curHist->GetXaxis()->GetXmax();
if ((mean < xmin || mean > xmax) && rms > (xmax-xmin)) {
mean = 0.5*(xmax+xmin);
rms = 0.5*(xmax-xmin);
}
TF1 *f1 = (TF1*)hFitter->GetUserFunc();
f1->SetParameter(0,constant);
f1->SetParameter(1,mean);
f1->SetParameter(2,rms);
f1->SetParLimits(2,0,10*rms);
}
//______________________________________________________________________________
void H1InitExpo()
{
// -*-*-*-*Compute Initial values of parameters for an exponential*-*-*-*-*
// =======================================================
Double_t constant, slope;
Int_t ifail;
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
Int_t nchanx = hxlast - hxfirst + 1;
H1LeastSquareLinearFit(-nchanx, constant, slope, ifail);
TF1 *f1 = (TF1*)hFitter->GetUserFunc();
f1->SetParameter(0,constant);
f1->SetParameter(1,slope);
}
//______________________________________________________________________________
void H1InitPolynom()
{
// -*-*-*-*Compute Initial values of parameters for a polynom*-*-*-*-*-*-*
// ===================================================
Double_t fitpar[25];
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
TF1 *f1 = (TF1*)hFitter->GetUserFunc();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
Int_t nchanx = hxlast - hxfirst + 1;
Int_t npar = f1->GetNpar();
if (nchanx <=1 || npar == 1) {
TH1 *curHist = (TH1*)hFitter->GetObjectFit();
fitpar[0] = curHist->GetSumOfWeights()/Double_t(nchanx);
} else {
H1LeastSquareFit( nchanx, npar, fitpar);
}
for (Int_t i=0;i<npar;i++) f1->SetParameter(i, fitpar[i]);
}
//______________________________________________________________________________
void H1LeastSquareFit(Int_t n, Int_t m, Double_t *a)
{
// -*-*-*-*-*-*Least squares lpolynomial fitting without weights*-*-*-*-*-*-*
// =================================================
//
// n number of points to fit
// m number of parameters
// a array of parameters
//
// based on CERNLIB routine LSQ: Translated to C++ by Rene Brun
// (E.Keil. revised by B.Schorr, 23.10.1981.)
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
const Double_t zero = 0.;
const Double_t one = 1.;
const Int_t idim = 20;
Double_t b[400] /* was [20][20] */;
Int_t i, k, l, ifail;
Double_t power;
Double_t da[20], xk, yk;
if (m <= 2) {
H1LeastSquareLinearFit(n, a[0], a[1], ifail);
return;
}
if (m > idim || m > n) return;
b[0] = Double_t(n);
da[0] = zero;
for (l = 2; l <= m; ++l) {
b[l-1] = zero;
b[m + l*20 - 21] = zero;
da[l-1] = zero;
}
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
TH1 *curHist = (TH1*)hFitter->GetObjectFit();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
for (k = hxfirst; k <= hxlast; ++k) {
xk = curHist->GetBinCenter(k);
yk = curHist->GetBinContent(k);
power = one;
da[0] += yk;
for (l = 2; l <= m; ++l) {
power *= xk;
b[l-1] += power;
da[l-1] += power*yk;
}
for (l = 2; l <= m; ++l) {
power *= xk;
b[m + l*20 - 21] += power;
}
}
for (i = 3; i <= m; ++i) {
for (k = i; k <= m; ++k) {
b[k - 1 + (i-1)*20 - 21] = b[k + (i-2)*20 - 21];
}
}
H1LeastSquareSeqnd(m, b, idim, ifail, 1, da);
for (i=0; i<m; ++i) a[i] = da[i];
}
//______________________________________________________________________________
void H1LeastSquareLinearFit(Int_t ndata, Double_t &a0, Double_t &a1, Int_t &ifail)
{
// -*-*-*-*-*-*-*-*Least square linear fit without weights*-*-*-*-*-*-*-*-*
// =======================================
//
// extracted from CERNLIB LLSQ: Translated to C++ by Rene Brun
// (added to LSQ by B. Schorr, 15.02.1982.)
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Double_t xbar, ybar, x2bar;
Int_t i, n;
Double_t xybar;
Double_t fn, xk, yk;
Double_t det;
n = TMath::Abs(ndata);
ifail = -2;
xbar = ybar = x2bar = xybar = 0;
TVirtualFitter *hFitter = TVirtualFitter::GetFitter();
TH1 *curHist = (TH1*)hFitter->GetObjectFit();
Int_t hxfirst = hFitter->GetXfirst();
Int_t hxlast = hFitter->GetXlast();
for (i = hxfirst; i <= hxlast; ++i) {
xk = curHist->GetBinCenter(i);
yk = curHist->GetBinContent(i);
if (ndata < 0) {
if (yk <= 0) yk = 1e-9;
yk = TMath::Log(yk);
}
xbar += xk;
ybar += yk;
x2bar += xk*xk;
xybar += xk*yk;
}
fn = Double_t(n);
det = fn*x2bar - xbar*xbar;
ifail = -1;
if (det <= 0) {
a0 = ybar/fn;
a1 = 0;
return;
}
ifail = 0;
a0 = (x2bar*ybar - xbar*xybar) / det;
a1 = (fn*xybar - xbar*ybar) / det;
}
//______________________________________________________________________________
void H1LeastSquareSeqnd(Int_t n, Double_t *a, Int_t idim, Int_t &ifail, Int_t k, Double_t *b)
{
// -*-*-*-*-*-*Extracted from CERN Program library routine DSEQN*-*-*-*-*-*
// =================================================
//
// : Translated to C++ by Rene Brun
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t a_dim1, a_offset, b_dim1, b_offset;
Int_t nmjp1, i, j, l;
Int_t im1, jp1, nm1, nmi;
Double_t s1, s21, s22;
const Double_t one = 1.;
/* Parameter adjustments */
b_dim1 = idim;
b_offset = b_dim1 + 1;
b -= b_offset;
a_dim1 = idim;
a_offset = a_dim1 + 1;
a -= a_offset;
if (idim < n) return;
ifail = 0;
for (j = 1; j <= n; ++j) {
if (a[j + j*a_dim1] <= 0) { ifail = -1; return; }
a[j + j*a_dim1] = one / a[j + j*a_dim1];
if (j == n) continue;
jp1 = j + 1;
for (l = jp1; l <= n; ++l) {
a[j + l*a_dim1] = a[j + j*a_dim1] * a[l + j*a_dim1];
s1 = -a[l + (j+1)*a_dim1];
for (i = 1; i <= j; ++i) { s1 = a[l + i*a_dim1] * a[i + (j+1)*a_dim1] + s1; }
a[l + (j+1)*a_dim1] = -s1;
}
}
if (k <= 0) return;
for (l = 1; l <= k; ++l) {
b[l*b_dim1 + 1] = a[a_dim1 + 1]*b[l*b_dim1 + 1];
}
if (n == 1) return;
for (l = 1; l <= k; ++l) {
for (i = 2; i <= n; ++i) {
im1 = i - 1;
s21 = -b[i + l*b_dim1];
for (j = 1; j <= im1; ++j) {
s21 = a[i + j*a_dim1]*b[j + l*b_dim1] + s21;
}
b[i + l*b_dim1] = -a[i + i*a_dim1]*s21;
}
nm1 = n - 1;
for (i = 1; i <= nm1; ++i) {
nmi = n - i;
s22 = -b[nmi + l*b_dim1];
for (j = 1; j <= i; ++j) {
nmjp1 = n - j + 1;
s22 = a[nmi + nmjp1*a_dim1]*b[nmjp1 + l*b_dim1] + s22;
}
b[nmi + l*b_dim1] = -s22;
}
}
}
//______________________________________________________________________________
Int_t TH1::GetBin(Int_t binx, Int_t biny, Int_t binz) const
{
// -*-*-*-*Return Global bin number corresponding to binx,y,z*-*-*-*-*-*-*
// ==================================================
//
// 2-D and 3-D histograms are represented with a one dimensional
// structure.
// This has the advantage that all existing functions, such as
// GetBinContent, GetBinError, GetBinFunction work for all dimensions.
//
// In case of a TH1x, returns binx directly.
//
// Convention for numbering bins
// =============================
// For all histogram types: nbins, xlow, xup
// bin = 0; underflow bin
// bin = 1; first bin with low-edge xlow INCLUDED
// bin = nbins; last bin with upper-edge xup EXCLUDED
// bin = nbins+1; overflow bin
// In case of 2-D or 3-D histograms, a "global bin" number is defined.
// For example, assuming a 3-D histogram with binx,biny,binz, the function
// Int_t bin = h->GetBin(binx,biny,binz);
// returns a global/linearized bin number. This global bin is useful
// to access the bin information independently of the dimension.
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t nx, ny, nz;
if (GetDimension() < 2) {
nx = fXaxis.GetNbins()+2;
if (binx < 0) binx = 0;
if (binx >= nx) binx = nx-1;
return binx;
}
if (GetDimension() < 3) {
nx = fXaxis.GetNbins()+2;
if (binx < 0) binx = 0;
if (binx >= nx) binx = nx-1;
ny = fYaxis.GetNbins()+2;
if (biny < 0) biny = 0;
if (biny >= ny) biny = ny-1;
return binx + nx*biny;
}
if (GetDimension() < 4) {
nx = fXaxis.GetNbins()+2;
if (binx < 0) binx = 0;
if (binx >= nx) binx = nx-1;
ny = fYaxis.GetNbins()+2;
if (biny < 0) biny = 0;
if (biny >= ny) biny = ny-1;
nz = fZaxis.GetNbins()+2;
if (binz < 0) binz = 0;
if (binz >= nz) binz = nz-1;
return binx + nx*(biny +ny*binz);
}
return -1;
}
//______________________________________________________________________________
Axis_t TH1::GetRandom() const
{
// return a random number distributed according the histogram bin contents.
// This function checks if the bins integral exists. If not, the integral
// is evaluated, normalized to one.
// The integral is automatically recomputed if the number of entries
// is not the same then when the integral was computed.
// NB Only valid for 1-d histograms. Use GetRandom2 or 3 otherwise.
if (fDimension > 1) {
Error("GetRandom","Function only valid for 1-d histograms");
return 0;
}
Int_t nbinsx = GetNbinsX();
Double_t integral;
if (fIntegral) {
if (fIntegral[nbinsx+1] != fEntries) integral = ((TH1*)this)->ComputeIntegral();
} else {
integral = ((TH1*)this)->ComputeIntegral();
if (integral == 0 || fIntegral == 0) return 0;
}
Double_t r1 = gRandom->Rndm();
Int_t ibin = TMath::BinarySearch(nbinsx,fIntegral,r1);
return GetBinLowEdge(ibin+1)
+GetBinWidth(ibin+1)*(r1-fIntegral[ibin])/(fIntegral[ibin+1] - fIntegral[ibin]);
}
//______________________________________________________________________________
Stat_t TH1::GetBinContent(Int_t) const
{
// -*-*-*-*-*Return content of bin number bin
// ================================
// Implemented in TH1C,S,F,D
//
// Convention for numbering bins
// =============================
// For all histogram types: nbins, xlow, xup
// bin = 0; underflow bin
// bin = 1; first bin with low-edge xlow INCLUDED
// bin = nbins; last bin with upper-edge xup EXCLUDED
// bin = nbins+1; overflow bin
// In case of 2-D or 3-D histograms, a "global bin" number is defined.
// For example, assuming a 3-D histogram with binx,biny,binz, the function
// Int_t bin = h->GetBin(binx,biny,binz);
// returns a global/linearized bin number. This global bin is useful
// to access the bin information independently of the dimension.
AbstractMethod("GetBinContent");
return 0;
}
//______________________________________________________________________________
Stat_t TH1::GetBinContent(Int_t binx, Int_t biny) const
{
// -*-*-*-*-*Return content of bin number binx, biny
// =======================================
// NB: Function to be called for 2-d histograms only
// see convention for numbering bins in TH1::GetBin
Int_t bin = GetBin(binx,biny);
return GetBinContent(bin);
}
//______________________________________________________________________________
Stat_t TH1::GetBinContent(Int_t binx, Int_t biny, Int_t binz) const
{
// -*-*-*-*-*Return content of bin number binx,biny,binz
// ===========================================
// NB: Function to be called for 3-d histograms only
// see convention for numbering bins in TH1::GetBin
Int_t bin = GetBin(binx,biny,binz);
return GetBinContent(bin);
}
//______________________________________________________________________________
TAxis *TH1::GetXaxis() const
{
// return a pointer to the X axis object
return &((TH1*)this)->fXaxis;
}
//______________________________________________________________________________
TAxis *TH1::GetYaxis() const
{
// return a pointer to the Y axis object
return &((TH1*)this)->fYaxis;
}
//______________________________________________________________________________
TAxis *TH1::GetZaxis() const
{
// return a pointer to the Z axis object
return &((TH1*)this)->fZaxis;
}
//___________________________________________________________________________
void TH1::LabelsDeflate(Option_t *ax)
{
// Reduce the number of bins for this axis to the number of bins having a label.
Int_t iaxis = AxisChoice(ax);
TAxis *axis = 0;
if (iaxis == 1) axis = GetXaxis();
if (iaxis == 2) axis = GetYaxis();
if (iaxis == 3) axis = GetZaxis();
if (!axis) return;
if (!axis->GetLabels()) return;
TIter next(axis->GetLabels());
TObject *obj;
Int_t nbins = 0;
while ((obj = next())) {
if (obj->GetUniqueID()) nbins++;
}
if (nbins < 1) nbins = 1;
TH1 *hold = (TH1*)Clone();
hold->SetDirectory(0);
Bool_t timedisp = axis->GetTimeDisplay();
Double_t xmin = axis->GetXmin();
Double_t xmax = axis->GetBinUpEdge(nbins);
if (xmax <= xmin) xmax = xmin +nbins;
axis->SetRange(0,0);
axis->Set(nbins,xmin,xmax);
//Int_t nbinsx = fXaxis.GetNbins();
//Int_t nbinsy = fYaxis.GetNbins();
//Int_t nbinsz = fZaxis.GetNbins();
Int_t nbinsx = hold->GetXaxis()->GetNbins();
Int_t nbinsy = hold->GetYaxis()->GetNbins();
Int_t nbinsz = hold->GetZaxis()->GetNbins();
Int_t ncells = nbinsx+2;
if (GetDimension() > 1) ncells *= nbinsy+2;
if (GetDimension() > 2) ncells *= nbinsz+2;
SetBinsLength(ncells);
Int_t errors = fSumw2.fN;
if (errors) fSumw2.Set(ncells);
axis->SetTimeDisplay(timedisp);
//now loop on all bins and refill
Double_t err,cu;
Int_t bin,ibin,binx,biny,binz;
Double_t oldEntries = fEntries;
for (binz=1;binz<=nbinsz;binz++) {
for (biny=1;biny<=nbinsy;biny++) {
for (binx=1;binx<=nbinsx;binx++) {
bin = hold->GetBin(binx,biny,binz);
ibin= GetBin(binx,biny,binz);
cu = hold->GetBinContent(bin);
SetBinContent(ibin,cu);
if (errors) {
err = hold->GetBinError(bin);
SetBinError(ibin,err);
}
}
}
}
fEntries = oldEntries;
delete hold;
}
//______________________________________________________________________________
void TH1::LabelsInflate(Option_t *ax)
{
// Double the number of bins for axis.
// Refill histogram
// This function is called by TAxis::FindBin(const char *label)
Int_t iaxis = AxisChoice(ax);
TAxis *axis = 0;
if (iaxis == 1) axis = GetXaxis();
if (iaxis == 2) axis = GetYaxis();
if (iaxis == 3) axis = GetZaxis();
if (!axis) return;
TH1 *hold = (TH1*)Clone();
hold->SetDirectory(0);
Bool_t timedisp = axis->GetTimeDisplay();
Int_t nbxold = fXaxis.GetNbins();
Int_t nbyold = fYaxis.GetNbins();
Int_t nbzold = fZaxis.GetNbins();
Int_t nbins = axis->GetNbins();
Double_t xmin = axis->GetXmin();
Double_t xmax = axis->GetXmax();
xmax = xmin + 2*(xmax-xmin);
axis->SetRange(0,0);
axis->Set(2*nbins,xmin,xmax);
Int_t nbinsx = fXaxis.GetNbins();
Int_t nbinsy = fYaxis.GetNbins();
Int_t nbinsz = fZaxis.GetNbins();
Int_t ncells = nbinsx+2;
if (GetDimension() > 1) ncells *= nbinsy+2;
if (GetDimension() > 2) ncells *= nbinsz+2;
SetBinsLength(ncells);
Int_t errors = fSumw2.fN;
if (errors) fSumw2.Set(ncells);
axis->SetTimeDisplay(timedisp);
//now loop on all bins and refill
Double_t err,cu;
Int_t bin,ibin,binx,biny,binz;
for (binz=1;binz<=nbinsz;binz++) {
for (biny=1;biny<=nbinsy;biny++) {
for (binx=1;binx<=nbinsx;binx++) {
bin = hold->GetBin(binx,biny,binz);
ibin= GetBin(binx,biny,binz);
if (binx > nbxold || biny > nbyold || binz > nbzold) bin = -1;
if (bin > 0) cu = hold->GetBinContent(bin);
else cu = 0;
SetBinContent(ibin,cu);
if (errors) {
if (bin > 0) err = hold->GetBinError(bin);
else err = 0;
SetBinError(ibin,err);
}
}
}
}
delete hold;
}
//______________________________________________________________________________
void TH1::LabelsOption(Option_t *option, Option_t *ax)
{
// Set option(s) to draw axis with labels
// option = "a" sort by alphabetic order
// = ">" sort by decreasing values
// = "<" sort by increasing values
// = "h" draw labels horizonthal
// = "v" draw labels vertical
// = "u" draw labels up (end of label right adjusted)
// = "d" draw labels down (start of label left adjusted)
Int_t iaxis = AxisChoice(ax);
TAxis *axis = 0;
if (iaxis == 1) axis = GetXaxis();
if (iaxis == 2) axis = GetYaxis();
if (iaxis == 3) axis = GetZaxis();
if (!axis) return;
THashList *labels = axis->GetLabels();
if (!labels) {
Warning("LabelsOption","Cannot sort. No labels");
return;
}
TString opt = option;
opt.ToLower();
if (opt.Contains("h")) {
axis->SetBit(TAxis::kLabelsHori);
axis->ResetBit(TAxis::kLabelsVert);
axis->ResetBit(TAxis::kLabelsDown);
axis->ResetBit(TAxis::kLabelsUp);
}
if (opt.Contains("v")) {
axis->SetBit(TAxis::kLabelsVert);
axis->ResetBit(TAxis::kLabelsHori);
axis->ResetBit(TAxis::kLabelsDown);
axis->ResetBit(TAxis::kLabelsUp);
}
if (opt.Contains("u")) {
axis->SetBit(TAxis::kLabelsUp);
axis->ResetBit(TAxis::kLabelsVert);
axis->ResetBit(TAxis::kLabelsDown);
axis->ResetBit(TAxis::kLabelsHori);
}
if (opt.Contains("d")) {
axis->SetBit(TAxis::kLabelsDown);
axis->ResetBit(TAxis::kLabelsVert);
axis->ResetBit(TAxis::kLabelsHori);
axis->ResetBit(TAxis::kLabelsUp);
}
Int_t sort = -1;
if (opt.Contains("a")) sort = 0;
if (opt.Contains(">")) sort = 1;
if (opt.Contains("<")) sort = 2;
if (sort < 0) return;
if (sort > 0 && GetDimension() > 2) {
Error("LabelsOption","Sorting by value not implemented for 3-D histograms");
return;
}
Int_t n = TMath::Min(axis->GetNbins(), labels->GetSize());
Int_t *a = new Int_t[n+2];
Int_t i,j,k;
Double_t *cont = 0;
Double_t *errors = 0;
THashList *labold = new THashList(labels->GetSize(),1);
TIter nextold(labels);
TObject *obj;
while ((obj=nextold())) {
labold->Add(obj);
}
labels->Clear();
if (sort > 0) {
//---sort by values of bins
if (GetDimension() == 1) {
cont = new Double_t[n];
if (fSumw2.fN) errors = new Double_t[n];
for (i=1;i<=n;i++) {
cont[i-1] = GetBinContent(i);
if (errors) errors[i-1] = GetBinError(i);
}
if (sort ==1) TMath::Sort(n,cont,a,kTRUE); //sort by decreasing values
else TMath::Sort(n,cont,a,kFALSE); //sort by increasing values
for (i=1;i<=n;i++) {
SetBinContent(i,cont[a[i-1]]);
if (errors) SetBinError(i,errors[a[i-1]]);
}
for (i=1;i<=n;i++) {
obj = labold->At(a[i-1]);
labels->Add(obj);
obj->SetUniqueID(i);
}
} else if (GetDimension()== 2) {
Double_t *pcont = new Double_t[n+2];
for (i=0;i<=n;i++) pcont[i] = 0;
Int_t nx = fXaxis.GetNbins();
Int_t ny = fYaxis.GetNbins();
cont = new Double_t[(nx+2)*(ny+2)];
if (fSumw2.fN) errors = new Double_t[n];
for (i=1;i<=nx;i++) {
for (j=1;j<=ny;j++) {
cont[i+nx*j] = GetBinContent(i,j);
if (errors) errors[i+nx*j] = GetBinError(i,j);
if (axis == GetXaxis()) k = i;
else k = j;
pcont[k-1] += cont[i+nx*j];
}
}
if (sort ==1) TMath::Sort(n,pcont,a,kTRUE); //sort by decreasing values
else TMath::Sort(n,pcont,a,kFALSE); //sort by increasing values
for (i=0;i<n;i++) {
obj = labold->At(a[i]);
labels->Add(obj);
obj->SetUniqueID(i+1);
}
delete [] pcont;
for (i=1;i<=nx;i++) {
for (j=1;j<=ny;j++) {
if (axis == GetXaxis()) {
SetBinContent(i,j,cont[a[i-1]+1+nx*j]);
if (errors) SetBinError(i,j,errors[a[i-1]+1+nx*j]);
} else {
SetBinContent(i,j,cont[i+nx*(a[j-1]+1)]);
if (errors) SetBinError(i,j,errors[i+nx*(a[j-1]+1)]);
}
}
}
} else {
//to be implemented
}
} else {
//---alphabetic sort
const UInt_t kUsed = 1<<18;
TObject *objk=0;
a[0] = 0;
a[n+1] = n+1;
for (i=1;i<=n;i++) {
const char *label = "zzzzzzzzzzzz";
for (j=1;j<=n;j++) {
obj = labold->At(j-1);
if (!obj) continue;
if (obj->TestBit(kUsed)) continue;
//use strcasecmp for case non-sensitive sort (may be an option)
if (strcmp(label,obj->GetName()) < 0) continue;
objk = obj;
a[i] = j;
label = obj->GetName();
}
if (objk) {
objk->SetUniqueID(i);
labels->Add(objk);
objk->SetBit(kUsed);
}
}
for (i=1;i<=n;i++) {
obj = labels->At(i-1);
if (!obj) continue;
obj->ResetBit(kUsed);
}
if (GetDimension() == 1) {
cont = new Double_t[n+2];
if (fSumw2.fN) errors = new Double_t[n+2];
for (i=1;i<=n;i++) {
cont[i] = GetBinContent(a[i]);
if (errors) errors[i] = GetBinError(a[i]);
}
for (i=1;i<=n;i++) {
SetBinContent(i,cont[i]);
if (errors) SetBinError(i,errors[i]);
}
} else if (GetDimension()== 2) {
Int_t nx = fXaxis.GetNbins()+2;
Int_t ny = fYaxis.GetNbins()+2;
cont = new Double_t[nx*ny];
if (fSumw2.fN) errors = new Double_t[nx*ny];
for (i=0;i<nx;i++) {
for (j=0;j<ny;j++) {
cont[i+nx*j] = GetBinContent(i,j);
if (errors) errors[i+nx*j] = GetBinError(i,j);
}
}
for (i=0;i<nx;i++) {
for (j=0;j<ny;j++) {
if (axis == GetXaxis()) {
SetBinContent(i,j,cont[a[i]+nx*j]);
if (errors) SetBinError(i,j,errors[a[i]+nx*j]);
} else {
SetBinContent(i,j,cont[i+nx*a[j]]);
if (errors) SetBinError(i,j,errors[i+nx*a[j]]);
}
}
}
} else {
Int_t nx = fXaxis.GetNbins()+2;
Int_t ny = fYaxis.GetNbins()+2;
Int_t nz = fZaxis.GetNbins()+2;
cont = new Double_t[nx*ny*nz];
if (fSumw2.fN) errors = new Double_t[nx*ny*nz];
for (i=0;i<nx;i++) {
for (j=0;j<ny;j++) {
for (k=0;k<nz;k++) {
cont[i+nx*(j+ny*k)] = GetBinContent(i,j,k);
if (errors) errors[i+nx*(j+ny*k)] = GetBinError(i,j,k);
}
}
}
for (i=0;i<nx;i++) {
for (j=0;j<ny;j++) {
for (k=0;k<nz;k++) {
if (axis == GetXaxis()) {
SetBinContent(i,j,k,cont[a[i]+nx*(j+ny*k)]);
if (errors) SetBinError(i,j,k,errors[a[i]+nx*(j+ny*k)]);
} else if (axis == GetYaxis()) {
SetBinContent(i,j,k,cont[i+nx*(a[j]+ny*k)]);
if (errors) SetBinError(i,j,k,errors[i+nx*(a[j]+ny*k)]);
} else {
SetBinContent(i,j,k,cont[i+nx*(j+ny*a[k])]);
if (errors) SetBinError(i,j,k,errors[i+nx*(j+ny*a[k])]);
}
}
}
}
}
}
delete labold;
if (a) delete [] a;
if (cont) delete [] cont;
if (errors) delete [] errors;
}
//______________________________________________________________________________
static Bool_t AlmostEqual(Double_t a, Double_t b, Double_t epsilon = 0.00000001)
{
return TMath::Abs(a - b) < epsilon;
}
//______________________________________________________________________________
static Bool_t AlmostInteger(Double_t a, Double_t epsilon = 0.00000001)
{
return AlmostEqual(a - TMath::Floor(a), 0, epsilon) ||
AlmostEqual(a - TMath::Floor(a), 1, epsilon);
}
//______________________________________________________________________________
Bool_t TH1::SameLimitsAndNBins(const TAxis& axis1, const TAxis& axis2)
{
if ((axis1.GetNbins() == axis2.GetNbins())
&& (axis1.GetXmin() == axis2.GetXmin())
&& (axis1.GetXmax() == axis2.GetXmax()))
return kTRUE;
else
return kFALSE;
}
//______________________________________________________________________________
Bool_t TH1::RecomputeAxisLimits(TAxis& destAxis, const TAxis& anAxis)
{
// Finds new limits for the axis for the Merge function.
// returns false if the limits are incompatible
if (SameLimitsAndNBins(destAxis, anAxis))
return kTRUE;
if (destAxis.GetXbins()->fN || anAxis.GetXbins()->fN)
return kFALSE; // user binning not supported
Axis_t width1 = destAxis.GetBinWidth(0);
Axis_t width2 = anAxis.GetBinWidth(0);
if (width1 == 0 || width2 == 0)
return kFALSE; // no binning not supported
Axis_t xmin = TMath::Min(destAxis.GetXmin(), anAxis.GetXmin());
Axis_t xmax = TMath::Max(destAxis.GetXmax(), anAxis.GetXmax());
Axis_t width = TMath::Max(width1, width2);
// check the bin size
if (!AlmostInteger(width/width1) || !AlmostInteger(width/width2))
return kFALSE;
// check the limits
Axis_t delta;
delta = (destAxis.GetXmin() - xmin)/width1;
if (!AlmostInteger(delta))
xmin -= (TMath::Ceil(delta) - delta)*width1;
delta = (anAxis.GetXmin() - xmin)/width2;
if (!AlmostInteger(delta))
xmin -= (TMath::Ceil(delta) - delta)*width2;
delta = (destAxis.GetXmin() - xmin)/width1;
if (!AlmostInteger(delta))
return kFALSE;
delta = (xmax - destAxis.GetXmax())/width1;
if (!AlmostInteger(delta))
xmax += (TMath::Ceil(delta) - delta)*width1;
delta = (xmax - anAxis.GetXmax())/width2;
if (!AlmostInteger(delta))
xmax += (TMath::Ceil(delta) - delta)*width2;
delta = (xmax - destAxis.GetXmax())/width1;
if (!AlmostInteger(delta))
return kFALSE;
#ifdef DEBUG
if (!AlmostInteger((xmax - xmin) / width)) { // unnecessary check
printf("TH1::RecomputeAxisLimits - Impossible\n");
return kFALSE;
}
#endif
destAxis.Set(TMath::Nint((xmax - xmin)/width), xmin, xmax);
return kTRUE;
}
//______________________________________________________________________________
Long64_t TH1::Merge(TCollection *li)
{
// Add all histograms in the collection to this histogram.
// This function computes the min/max for the x axis,
// compute a new number of bins, if necessary,
// add bin contents, errors and statistics.
// If all histograms have bin labels, bins with identical labels
// will be merged, no matter what their order is.
// If overflows are present and limits are different the function will fail.
// The function returns the total number of entries in the result histogram
// if the merge is successfull, -1 otherwise.
//
// IMPORTANT remark. The axis x may have different number
// of bins and different limits, BUT the largest bin width must be
// a multiple of the smallest bin width and the upper limit must also
// be a multiple of the bin width.
// Example:
// void atest() {
// TH1F *h1 = new TH1F("h1","h1",110,-110,0);
// TH1F *h2 = new TH1F("h2","h2",220,0,110);
// TH1F *h3 = new TH1F("h3","h3",330,-55,55);
// TRandom r;
// for (Int_t i=0;i<10000;i++) {
// h1->Fill(r.Gaus(-55,10));
// h2->Fill(r.Gaus(55,10));
// h3->Fill(r.Gaus(0,10));
// }
//
// TList *list = new TList;
// list->Add(h1);
// list->Add(h2);
// list->Add(h3);
// TH1F *h = (TH1F*)h1->Clone("h");
// h->Reset();
// h.Merge(list);
// h->Draw();
// }
if (!li) return 0;
if (li->IsEmpty()) return (Int_t) GetEntries();
TList inlist;
TH1* hclone = (TH1*)Clone("FirstClone");
BufferEmpty(1); // To remove buffer.
Reset(); // BufferEmpty sets limits so we can't use it later.
SetEntries(0);
inlist.Add(hclone);
inlist.AddAll(li);
THashList allLabels;
THashList* labels=GetXaxis()->GetLabels();
Bool_t haveOneLabel=kFALSE;
if (labels) {
TIter iL(labels);
TObjString* lb;
while ((lb=(TObjString*)iL())) {
haveOneLabel |= (lb && lb->String().Length());
if (!allLabels.FindObject(lb))
allLabels.Add(lb);
}
}
TAxis newXAxis;
Bool_t initialLimitsFound = kFALSE;
Bool_t allHaveLabels = haveOneLabel;
Bool_t same = kTRUE;
Bool_t allHaveLimits = kTRUE;
TIter next(&inlist);
while (TObject *o = next()) {
TH1* h = dynamic_cast<TH1*> (o);
if (!h) {
Error("Add","Attempt to add object of class: %s to a %s",
o->ClassName(),this->ClassName());
return -1;
}
Bool_t hasLimits = h->GetXaxis()->GetXmin() < h->GetXaxis()->GetXmax();
allHaveLimits = allHaveLimits && hasLimits;
if (hasLimits) {
h->BufferEmpty();
if (!initialLimitsFound) {
initialLimitsFound = kTRUE;
newXAxis.Set(h->GetXaxis()->GetNbins(), h->GetXaxis()->GetXmin(),
h->GetXaxis()->GetXmax());
}
else {
if (!RecomputeAxisLimits(newXAxis, *(h->GetXaxis()))) {
Error("Merge", "Cannot merge histograms - limits are inconsistent:\n "
"first: (%d, %f, %f), second: (%d, %f, %f)",
newXAxis.GetNbins(), newXAxis.GetXmin(), newXAxis.GetXmax(),
h->GetXaxis()->GetNbins(), h->GetXaxis()->GetXmin(),
h->GetXaxis()->GetXmax());
}
}
}
if (allHaveLabels) {
THashList* labels=h->GetXaxis()->GetLabels();
Bool_t haveOneLabel=kFALSE;
if (labels) {
TIter iL(labels);
TObjString* lb;
while ((lb=(TObjString*)iL())) {
haveOneLabel |= (lb && lb->String().Length());
if (!allLabels.FindObject(lb)) {
allLabels.Add(lb);
same = kFALSE;
}
}
}
allHaveLabels&=(labels && haveOneLabel);
if (!allHaveLabels)
Warning("Merge","Not all histograms have labels. I will ignore labels,"
" falling back to bin numbering mode.");
}
}
next.Reset();
same = same && SameLimitsAndNBins(newXAxis, *GetXaxis());
if (!same && initialLimitsFound)
SetBins(newXAxis.GetNbins(), newXAxis.GetXmin(), newXAxis.GetXmax());
if (!allHaveLimits) {
// fill this histogram with all the data from buffers of histograms without limits
while (TH1* h = (TH1*)next()) {
if (h->GetXaxis()->GetXmin() >= h->GetXaxis()->GetXmax() && h->fBuffer) {
// no limits
Int_t nbentries = (Int_t)h->fBuffer[0];
for (Int_t i = 0; i < nbentries; i++)
Fill(h->fBuffer[2*i + 2], h->fBuffer[2*i + 1]);
// Entries from buffers have to be filled one by one
// because FillN doesn't resize histograms.
}
}
if (!initialLimitsFound)
return (Int_t) GetEntries(); // all histograms have been processed
next.Reset();
}
//merge bin contents and errors
Stat_t stats[kNstat], totstats[kNstat];
for (Int_t i=0;i<kNstat;i++) {totstats[i] = stats[i] = 0;}
GetStats(totstats);
Stat_t nentries = GetEntries();
Int_t binx, ix, nx;
Double_t cu;
Bool_t canRebin=TestBit(kCanRebin);
ResetBit(kCanRebin); // reset, otherwise setting the under/overflow will rebin
while (TH1* h=(TH1*)next()) {
// process only if the histogram has limits; otherwise it was processed before
if (h->GetXaxis()->GetXmin() < h->GetXaxis()->GetXmax()) {
// import statistics
h->GetStats(stats);
for (Int_t i=0;i<kNstat;i++)
totstats[i] += stats[i];
nentries += h->GetEntries();
nx = h->GetXaxis()->GetNbins();
for (binx = 0; binx <= nx + 1; binx++) {
cu = h->GetBinContent(binx);
if (!allHaveLabels || !binx || binx==nx+1) {
if ((!same) && (binx == 0 || binx == nx + 1)) {
if (cu != 0) {
Error("Merge", "Cannot merge histograms - the histograms have"
" different limits and undeflows/overflows are present."
" The initial histogram is now broken!");
return -1;
}
}
ix = fXaxis.FindBin(h->GetXaxis()->GetBinCenter(binx));
} else {
const char* label=h->GetXaxis()->GetBinLabel(binx);
if (!label) label="";
ix = fXaxis.FindBin(label);
}
AddBinContent(ix,cu);
if (fSumw2.fN) {
Double_t error1 = h->GetBinError(binx);
fSumw2.fArray[ix] += error1*error1;
}
}
}
}
if (canRebin) SetBit(kCanRebin);
//copy merged stats
PutStats(totstats);
SetEntries(nentries);
if (hclone) delete hclone;
return (Long64_t)nentries;
}
//______________________________________________________________________________
void TH1::Multiply(TF1 *f1, Double_t c1)
{
// Performs the operation: this = this*c1*f1
// if errors are defined (see TH1::Sumw2), errors are also recalculated.
//
// Only bins inside the function range are recomputed.
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Multiply
if (!f1) {
Error("Add","Attempt to multiply by a non-existing function");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// - Add statistics
Double_t nEntries = fEntries;
Stat_t s1[10];
Int_t i;
for (i=0;i<10;i++) {s1[i] = 0;}
PutStats(s1);
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t cu,w;
Double_t xx[3];
Double_t *params = 0;
f1->InitArgs(xx,params);
for (binz=0;binz<=nbinsz+1;binz++) {
xx[2] = fZaxis.GetBinCenter(binz);
for (biny=0;biny<=nbinsy+1;biny++) {
xx[1] = fYaxis.GetBinCenter(biny);
for (binx=0;binx<=nbinsx+1;binx++) {
xx[0] = fXaxis.GetBinCenter(binx);
if (!f1->IsInside(xx)) continue;
TF1::RejectPoint(kFALSE);
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
Double_t error1 = GetBinError(bin);
cu = c1*f1->EvalPar(xx);
if (TF1::RejectedPoint()) continue;
w = GetBinContent(bin)*cu;
SetBinContent(bin,w);
if (fSumw2.fN) {
fSumw2.fArray[bin] = cu*cu*error1*error1;
}
}
}
}
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Multiply(const TH1 *h1)
{
// -*-*-*-*-*-*-*-*-*Multiply this histogram by h1*-*-*-*-*-*-*-*-*-*-*-*-*
// =============================
//
// this = this*h1
//
// If errors of this are available (TH1::Sumw2), errors are recalculated.
// Note that if h1 has Sumw2 set, Sumw2 is automatically called for this
// if not already set.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Multiply
if (!h1) {
Error("Multiply","Attempt to multiply by a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()) {
Error("Multiply","Attempt to multiply histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Multiply","Attempt to multiply histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 has Sumw2 set
if (fSumw2.fN == 0 && h1->GetSumw2N() != 0) Sumw2();
// - Reset statistics
Double_t nEntries = fEntries;
fEntries = fTsumw = 0;
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t c0,c1,w;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = GetBin(binx,biny,binz);
c0 = GetBinContent(bin);
c1 = h1->GetBinContent(bin);
w = c0*c1;
SetBinContent(bin,w);
fEntries++;
if (fSumw2.fN) {
Double_t e0 = GetBinError(bin);
Double_t e1 = h1->GetBinError(bin);
fSumw2.fArray[bin] = (e0*e0*c1*c1 + e1*e1*c0*c0);
}
}
}
}
Stat_t s[kNstat];
GetStats(s);
PutStats(s);
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Multiply(const TH1 *h1, const TH1 *h2, Double_t c1, Double_t c2, Option_t *option)
{
// -*-*-*Replace contents of this histogram by multiplication of h1 by h2*-*
// ================================================================
//
// this = (c1*h1)*(c2*h2)
//
// If errors of this are available (TH1::Sumw2), errors are recalculated.
// Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this
// if not already set.
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Multiply
TString opt = option;
opt.ToLower();
// Bool_t binomial = kFALSE;
// if (opt.Contains("b")) binomial = kTRUE;
if (!h1 || !h2) {
Error("Multiply","Attempt to multiply by a non-existing histogram");
return;
}
Int_t nbinsx = GetNbinsX();
Int_t nbinsy = GetNbinsY();
Int_t nbinsz = GetNbinsZ();
// - Check histogram compatibility
if (nbinsx != h1->GetNbinsX() || nbinsy != h1->GetNbinsY() || nbinsz != h1->GetNbinsZ()
|| nbinsx != h2->GetNbinsX() || nbinsy != h2->GetNbinsY() || nbinsz != h2->GetNbinsZ()) {
Error("Multiply","Attempt to multiply histograms with different number of bins");
return;
}
// - Issue a Warning if histogram limits are different
if (fXaxis.GetXmin() != h1->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h1->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h1->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h1->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h1->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h1->fZaxis.GetXmax()) {
Warning("Multiply","Attempt to multiply histograms with different axis limits");
}
if (fXaxis.GetXmin() != h2->fXaxis.GetXmin() ||
fXaxis.GetXmax() != h2->fXaxis.GetXmax() ||
fYaxis.GetXmin() != h2->fYaxis.GetXmin() ||
fYaxis.GetXmax() != h2->fYaxis.GetXmax() ||
fZaxis.GetXmin() != h2->fZaxis.GetXmin() ||
fZaxis.GetXmax() != h2->fZaxis.GetXmax()) {
Warning("Multiply","Attempt to multiply histograms with different axis limits");
}
if (fDimension < 2) nbinsy = -1;
if (fDimension < 3) nbinsz = -1;
// Create Sumw2 if h1 or h2 have Sumw2 set
if (fSumw2.fN == 0 && (h1->GetSumw2N() != 0 || h2->GetSumw2N() != 0)) Sumw2();
// - Reset statistics
Double_t nEntries = fEntries;
fEntries = fTsumw = fTsumw2 = fTsumwx = fTsumwx2 = 0;
SetMinimum();
SetMaximum();
// Reset the kCanRebin option. Otherwise SetBinContent on the overflow bin
// would resize the axis limits!
ResetBit(kCanRebin);
// - Loop on bins (including underflows/overflows)
Int_t bin, binx, biny, binz;
Double_t b1,b2,w,d1,d2;
d1 = c1*c1;
d2 = c2*c2;
for (binz=0;binz<=nbinsz+1;binz++) {
for (biny=0;biny<=nbinsy+1;biny++) {
for (binx=0;binx<=nbinsx+1;binx++) {
bin = binx +(nbinsx+2)*(biny + (nbinsy+2)*binz);
b1 = h1->GetBinContent(bin);
b2 = h2->GetBinContent(bin);
w = (c1*b1)*(c2*b2);
SetBinContent(bin,w);
fEntries++;
if (fSumw2.fN) {
Double_t e1 = h1->GetBinError(bin);
Double_t e2 = h2->GetBinError(bin);
fSumw2.fArray[bin] = d1*d2*(e1*e1*b2*b2 + e2*e2*b1*b1);
}
}
}
}
Stat_t s[kNstat];
GetStats(s);
PutStats(s);
SetEntries(nEntries);
}
//______________________________________________________________________________
void TH1::Paint(Option_t *option)
{
// -*-*-*-*-*-*-*Control routine to paint any kind of histograms*-*-*-*-*-*-*
// ===============================================
//
// This function is automatically called by TCanvas::Update.
// (see TH1::Draw for the list of options)
GetPainter();
if (fPainter) {
if (strlen(option) > 0) fPainter->Paint(option);
else fPainter->Paint(fOption.Data());
}
}
//______________________________________________________________________________
TH1 *TH1::Rebin(Int_t ngroup, const char*newname)
{
// -*-*-*Rebin this histogram grouping ngroup bins together*-*-*-*-*-*-*-*-*
// ==================================================
// if newname is not blank a new temporary histogram hnew is created.
// else the current histogram is modified (default)
// The parameter ngroup indicates how many bins of this have to me merged
// into one bin of hnew
// If the original histogram has errors stored (via Sumw2), the resulting
// histograms has new errors correctly calculated.
//
// examples: if h1 is an existing TH1F histogram with 100 bins
// h1->Rebin(); //merges two bins in one in h1: previous contents of h1 are lost
// h1->Rebin(5); //merges five bins in one in h1
// TH1F *hnew = h1->Rebin(5,"hnew"); // creates a new histogram hnew
// //merging 5 bins of h1 in one bin
//
// NOTE: If ngroup is not an exact divider of the number of bins,
// the top limit of the rebinned histogram is changed
// to the upper edge of the bin=newbins*ngroup and the corresponding
// bins are added to the overflow bin.
// Statistics will be recomputed from the new bin contents.
Int_t nbins = fXaxis.GetNbins();
Axis_t xmin = fXaxis.GetXmin();
Axis_t xmax = fXaxis.GetXmax();
if ((ngroup <= 0) || (ngroup > nbins)) {
Error("Rebin", "Illegal value of ngroup=%d",ngroup);
return 0;
}
if (fDimension > 1 || InheritsFrom("TProfile")) {
Error("Rebin", "Operation valid on 1-D histograms only");
return 0;
}
Int_t newbins = nbins/ngroup;
// Save old bin contents into a new array
Double_t entries = fEntries;
Double_t *oldBins = new Double_t[nbins];
Int_t bin, i;
for (bin=0;bin<nbins;bin++) oldBins[bin] = GetBinContent(bin+1);
Double_t *oldErrors = 0;
if (fSumw2.fN != 0) {
oldErrors = new Double_t[nbins];
for (bin=0;bin<nbins;bin++) oldErrors[bin] = GetBinError(bin+1);
}
// create a clone of the old histogram if newname is specified
TH1 *hnew = this;
if (newname && strlen(newname) > 0) {
hnew = (TH1*)Clone();
hnew->SetName(newname);
}
// change axis specs and rebuild bin contents array::RebinAx
if(newbins*ngroup != nbins) {
xmax = fXaxis.GetBinUpEdge(newbins*ngroup);
hnew->fTsumw = 0; //stats must be reset because top bins will be moved to overflow bin
}
// save the TAttAxis members (reset by SetBins)
Int_t nDivisions = fXaxis.GetNdivisions();
Color_t axisColor = fXaxis.GetAxisColor();
Color_t labelColor = fXaxis.GetLabelColor();
Style_t labelFont = fXaxis.GetLabelFont();
Float_t labelOffset = fXaxis.GetLabelOffset();
Float_t labelSize = fXaxis.GetLabelSize();
Float_t tickLength = fXaxis.GetTickLength();
Float_t titleOffset = fXaxis.GetTitleOffset();
Float_t titleSize = fXaxis.GetTitleSize();
Color_t titleColor = fXaxis.GetTitleColor();
Style_t titleFont = fXaxis.GetTitleFont();
if(fXaxis.GetXbins()->GetSize() > 0){ // variable bin sizes
Axis_t *bins = new Axis_t[newbins+1];
for(Int_t i = 0; i <= newbins; ++i) bins[i] = fXaxis.GetBinLowEdge(1+i*ngroup);
hnew->SetBins(newbins,bins); //this also changes errors array (if any)
delete [] bins;
} else {
hnew->SetBins(newbins,xmin,xmax); //this also changes errors array (if any)
}
// Restore axis attributes
fXaxis.SetNdivisions(nDivisions);
fXaxis.SetAxisColor(axisColor);
fXaxis.SetLabelColor(labelColor);
fXaxis.SetLabelFont(labelFont);
fXaxis.SetLabelOffset(labelOffset);
fXaxis.SetLabelSize(labelSize);
fXaxis.SetTickLength(tickLength);
fXaxis.SetTitleOffset(titleOffset);
fXaxis.SetTitleSize(titleSize);
fXaxis.SetTitleColor(titleColor);
fXaxis.SetTitleFont(titleFont);
// copy merged bin contents (ignore under/overflows)
Int_t oldbin = 0;
Double_t binContent, binError;
for (bin = 0;bin<=newbins;bin++) {
binContent = 0;
binError = 0;
for (i=0;i<ngroup;i++) {
if (oldbin+i >= nbins) break;
binContent += oldBins[oldbin+i];
if (oldErrors) binError += oldErrors[oldbin+i]*oldErrors[oldbin+i];
}
hnew->SetBinContent(bin+1,binContent);
if (oldErrors) hnew->SetBinError(bin+1,TMath::Sqrt(binError));
oldbin += ngroup;
}
hnew->SetEntries(entries); //was modified by SetBinContent
delete [] oldBins;
if (oldErrors) delete [] oldErrors;
return hnew;
}
//______________________________________________________________________________
Bool_t TH1::FindNewAxisLimits(const TAxis* axis, const Axis_t point, Axis_t& newMin, Axis_t &newMax)
{
// finds new limits for the axis so that *point* is within the range and
// the limits are compatible with the previous ones (see TH1::Merge).
// new limits are put into *newMin* and *newMax* variables.
// axis - axis whose limits are to be recomputed
// point - point that should fit within the new axis limits
// newMin - new minimum will be stored here
// newMax - new maximum will be stored here.
// false if failed (e.g. if the initial axis limits are wrong
// or the new range is more than 2^64 times the old one).
Axis_t xmin = axis->GetXmin();
Axis_t xmax = axis->GetXmax();
if (xmin >= xmax) return kFALSE;
Axis_t range = xmax-xmin;
Axis_t binsize = range / axis->GetNbins();
//recompute new axis limits by doubling the current range
Int_t ntimes = 0;
while (point < xmin) {
if (ntimes++ > 64)
return kFALSE;
xmin = xmin - range;
range *= 2;
binsize *= 2;
// make sure that the merging will be correct
if ( xmin / binsize - TMath::Floor(xmin / binsize) >= 0.5) {
xmin += 0.5 * binsize;
xmax += 0.5 * binsize; // won't work with a histogram with only one bin, but I don't care
}
}
while (point >= xmax) {
if (ntimes++ > 64)
return kFALSE;
xmax = xmax + range;
range *= 2;
binsize *= 2;
// make sure that the merging will be correct
if ( xmin / binsize - TMath::Floor(xmin / binsize) >= 0.5) {
xmin -= 0.5 * binsize;
xmax -= 0.5 * binsize; // won't work with a histogram with only one bin, but I don't care
}
}
newMin = xmin;
newMax = xmax;
// Info("FindNewAxisLimits", "OldAxis: (%lf, %lf), new: (%lf, %lf), point: %lf",
// axis->GetXmin(), axis->GetXmax(), xmin, xmax, point);
return kTRUE;
}
//______________________________________________________________________________
void TH1::RebinAxis(Axis_t x, const char *ax)
{
// Histogram is resized along ax such that x is in the axis range.
// The new axis limits are recomputed by doubling iteratively
// the current axis range until the specified value x is within the limits.
// The algorithm makes a copy of the histogram, then loops on all bins
// of the old histogram to fill the rebinned histogram.
// Takes into account errors (Sumw2) if any.
// The algorithm works for 1-d, 2-d and 3-d histograms.
// The bit kCanRebin must be set before invoking this function.
// Ex: h->SetBit(TH1::kCanRebin);
if (!TestBit(kCanRebin)) return;
if (TMath::IsNaN(x)) { // x may be a NaN
ResetBit(kCanRebin);
return;
}
char achoice = toupper(ax[0]);
TAxis *axis = &fXaxis;
if (achoice == 'Y') axis = &fYaxis;
if (achoice == 'Z') axis = &fZaxis;
if (axis->GetXmin() >= axis->GetXmax()) return;
if (axis->GetNbins() <= 0) return;
Axis_t xmin, xmax;
if (!FindNewAxisLimits(axis, x, xmin, xmax))
return;
//save a copy of this histogram
TH1 *hold = (TH1*)Clone();
hold->SetDirectory(0);
//set new axis limits
axis->SetLimits(xmin,xmax);
Int_t nbinsx = fXaxis.GetNbins();
Int_t nbinsy = fYaxis.GetNbins();
Int_t nbinsz = fZaxis.GetNbins();
//now loop on all bins and refill
Double_t err,cu;
Axis_t bx,by,bz;
Int_t errors = GetSumw2N();
Int_t ix,iy,iz,ibin,binx,biny,binz,bin;
Reset("ICE"); //reset only Integral, contents and Errors
for (binz=1;binz<=nbinsz;binz++) {
bz = hold->GetZaxis()->GetBinCenter(binz);
iz = fZaxis.FindFixBin(bz);
for (biny=1;biny<=nbinsy;biny++) {
by = hold->GetYaxis()->GetBinCenter(biny);
iy = fYaxis.FindFixBin(by);
for (binx=1;binx<=nbinsx;binx++) {
bx = hold->GetXaxis()->GetBinCenter(binx);
ix = fXaxis.FindFixBin(bx);
bin = hold->GetBin(binx,biny,binz);
ibin= GetBin(ix,iy,iz);
cu = hold->GetBinContent(bin);
AddBinContent(ibin,cu);
if (errors) {
err = hold->GetBinError(bin);
fSumw2.fArray[ibin] += err*err;
}
}
}
}
delete hold;
}
//______________________________________________________________________________
void TH1::RecursiveRemove(TObject *obj)
{
// Recursively remove object from the list of functions
if (fFunctions) {
if (!fFunctions->TestBit(kInvalidObject)) fFunctions->RecursiveRemove(obj);
}
}
//______________________________________________________________________________
void TH1::Scale(Double_t c1)
{
// -*-*-*Multiply this histogram by a constant c1*-*-*-*-*-*-*-*-*
// ========================================
//
// this = c1*this
//
// Note that both contents and errors(if any) are scaled.
// This function uses the services of TH1::Add
//
// IMPORTANT NOTE: If you intend to use the errors of this histogram later
// you should call Sumw2 before making this operation.
// This is particularly important if you fit the histogram after TH1::Scale
Double_t ent = fEntries;
Add(this,this,c1,0);
fEntries = ent;
//if contours set, must also scale contours
Int_t ncontours = GetContour();
if (ncontours == 0) return;
Double_t *levels = fContour.GetArray();
for (Int_t i=0;i<ncontours;i++) {
levels[i] *= c1;
}
}
//______________________________________________________________________________
void TH1::SetDefaultBufferSize(Int_t buffersize)
{
// static function to set the default buffer size for automatic histograms.
// When an histogram is created with one of its axis lower limit greater
// or equal to its upper limit, the function SetBuffer is automatically
// called with the default buffer size.
if (buffersize < 0) buffersize = 0;
fgBufferSize = buffersize;
}
//______________________________________________________________________________
void TH1::SetTitle(const char *title)
{
// Change (i.e. set) the title
// if title is of the form "stringt;stringx;stringy;stringz"
// the histogram title is set to stringt,
// the x axis title to stringx, the y axis title to stringy,etc
fTitle = title;
// Decode fTitle. It may contain X, Y and Z titles
TString str1 = fTitle, str2;
Int_t isc = str1.Index(";");
Int_t lns = str1.Length();
if (isc >=0 ) {
fTitle = str1(0,isc);
str1 = str1(isc+1, lns);
isc = str1.Index(";");
if (isc >=0 ) {
str2 = str1(0,isc);
fXaxis.SetTitle(str2.Data());
lns = str1.Length();
str1 = str1(isc+1, lns);
isc = str1.Index(";");
if (isc >=0 ) {
str2 = str1(0,isc);
fYaxis.SetTitle(str2.Data());
lns = str1.Length();
str1 = str1(isc+1, lns);
fZaxis.SetTitle(str1.Data());
} else {
fYaxis.SetTitle(str1.Data());
}
} else {
fXaxis.SetTitle(str1.Data());
}
}
if (gPad && TestBit(kMustCleanup)) gPad->Modified();
}
// -------------------------------------------------------------------------
void TH1::SmoothArray(Int_t nn, Double_t *xx, Int_t ntimes)
{
// smooth array xx, translation of Hbook routine hsmoof.F
// based on algorithm 353QH twice presented by J. Friedman
// in Proc.of the 1974 CERN School of Computing, Norway, 11-24 August, 1974.
Int_t ii, jj, ik, jk, kk, nn1, nn2;
Double_t hh[6] = {0,0,0,0,0,0};
Double_t *yy = new Double_t[nn];
Double_t *zz = new Double_t[nn];
Double_t *rr = new Double_t[nn];
for (Int_t pass=0;pass<ntimes;pass++) {
// first copy original data into temp array
for (ii = 0; ii < nn; ii++) {
yy[ii] = xx[ii];
}
// do 353 i.e. running median 3, 5, and 3 in a single loop
for (kk = 1; kk <= 3; kk++) {
ik = 0;
if (kk == 2) ik = 1;
nn1 = ik + 2;
nn2 = nn - ik - 1;
// do all elements beside the first and last point for median 3
// and first two and last 2 for median 5
for (ii = nn1; ii <= nn2; ii++) {
for (jj = 0; jj < 3; jj++) {
hh[jj] = yy[ii + jj - 1];
}
zz[ii] = TMath::Median(3 + 2*ik, hh);
}
if (kk == 1) { // first median 3
// first point
hh[0] = 3*yy[1] - 2*yy[2];
hh[1] = yy[0];
hh[2] = yy[2];
zz[0] = TMath::Median(3, hh);
// last point
hh[0] = yy[nn - 2];
hh[1] = yy[nn - 1];
hh[2] = 3*yy[nn - 2] - 2*yy[nn - 3];
zz[nn - 1] = TMath::Median(3, hh);
}
if (kk == 2) { // median 5
// first point remains the same
zz[0] = yy[0];
for (ii = 0; ii < 3; ii++) {
hh[ii] = yy[ii];
}
zz[1] = TMath::Median(3, hh);
// last two points
for (ii = 0; ii < 3; ii++) {
hh[ii] = yy[nn +nn2 -1 + ii];
}
zz[nn - 2] = TMath::Median(3, hh);
zz[nn - 1] = yy[nn - 1];
}
}
// quadratic interpolation for flat segments
nn2 = nn2 - 2;
for (ii = nn1; ii <= nn2; ii++) {
if (zz[ii - 1] != zz[ii]) continue;
if (zz[ii] != zz[ii + 1]) continue;
hh[0] = zz[ii - 2] - zz[ii];
hh[1] = zz[ii + 2] - zz[ii];
if (hh[0] * hh[1] < 0) continue;
jk = 0;
if ( TMath::Abs(hh[1]) > TMath::Abs(hh[0]) ) jk = -1;
yy[ii] = -0.5*zz[ii - 2*jk] + zz[ii - jk]/0.75 + zz[ii + 2*jk] /6.;
yy[ii + jk] = 0.5*(zz[ii + 2*jk] - zz[ii - 2*jk]) + zz[ii - jk];
}
// running means
for (ii = 1; ii < nn - 1; ii++) {
rr[ii] = 0.25*yy[ii - 1] + 0.5*yy[ii] + 0.25*yy[ii + 1];
}
rr[0] = yy[0];
rr[nn - 1] = yy[nn - 1];
// now do the same for residuals
for (ii = 0; ii < nn; ii++) {
yy[ii] = xx[ii] - rr[ii];
}
// do 353 i.e. running median 3, 5, and 3 in a single loop
for (kk = 1; kk <= 3; kk++) {
ik = 0;
if (kk == 2) ik = 1;
nn1 = ik + 1;
nn2 = nn - ik - 1;
// do all elements beside the first and last point for median 3
// and first two and last 2 for median 5
for (ii = nn1; ii <= nn2; ii++) {
for (jj = 0; jj < 3; jj++) {
hh[jj] = yy[ii + jj - 1];
}
zz[ii] = TMath::Median(3 + 2*ik, hh);
}
if (kk == 1) { // first median 3
// first point
hh[0] = 3*yy[1] - 2*yy[2];
hh[1] = yy[0];
hh[2] = yy[2];
zz[0] = TMath::Median(3, hh);
// last point
hh[0] = yy[nn - 2];
hh[1] = yy[nn - 1];
hh[2] = 3*yy[nn - 2] - 2*yy[nn - 3];
zz[nn - 1] = TMath::Median(3, hh);
}
if (kk == 2) { // median 5
// first point remains the same
zz[0] = yy[0];
for (ii = 0; ii < 3; ii++) {
hh[ii] = yy[ii];
}
zz[1] = TMath::Median(3, hh);
// last two points
for (ii = 0; ii < 3; ii++) {
hh[ii] = yy[nn - 3 + ii];
}
zz[nn - 2] = TMath::Median(3, hh);
zz[nn - 1] = yy[nn - 1];
}
}
// quadratic interpolation for flat segments
nn2 = nn2 - 1;
for (ii = nn1 + 1; ii <= nn2; ii++) {
if (zz[ii - 1] != zz[ii]) continue;
if (zz[ii] != zz[ii + 1]) continue;
hh[0] = zz[ii - 2] - zz[ii];
hh[1] = zz[ii + 2] - zz[ii];
if (hh[0] * hh[1] < 0) continue;
jk = 0;
if ( TMath::Abs(hh[1]) > TMath::Abs(hh[0]) ) jk = -1;
yy[ii] = -0.5*zz[ii - 2*jk] + zz[ii - jk]/0.75 + zz[ii + 2*jk]/6.;
yy[ii + jk] = 0.5*(zz[ii + 2*jk] - zz[ii - 2*jk]) + zz[ii - jk];
}
// running means
for (ii = 1; ii <= nn - 1; ii++) {
zz[ii] = 0.25*yy[ii - 1] + 0.5*yy[ii] + 0.25*yy[ii + 1];
}
zz[0] = yy[0];
zz[nn - 1] = yy[nn - 1];
// add smoothed xx and smoothed residuals
for (ii = 0; ii < nn; ii++) {
if (xx[ii] < 0) xx[ii] = rr[ii] + zz[ii];
else xx[ii] = TMath::Abs(rr[ii] + zz[ii]);
}
}
delete [] yy;
delete [] zz;
delete [] rr;
}
// ------------------------------------------------------------------------
void TH1::Smooth(Int_t ntimes, Int_t firstbin, Int_t lastbin)
{
// Smooth bin contents of this histogram between firstbin and lastbin.
// (if firstbin=-1 and lastbin=-1 (default) all bins are smoothed.
// bin contents are replaced by their smooth values.
// Errors (if any) are not modified.
// algorithm can only be applied to 1-d histograms
if (fDimension != 1) {
Error("Smooth","Smooth only supported for 1-d histograms");
return;
}
Int_t nbins = fXaxis.GetNbins();
if (firstbin < 0) firstbin = 1;
if (lastbin < 0) lastbin = nbins;
if (lastbin > nbins+1) lastbin = nbins;
nbins = lastbin - firstbin + 1;
Double_t *xx = new Double_t[nbins];
Int_t i;
for (i=0;i<nbins;i++) {
xx[i] = GetBinContent(i+firstbin);
}
TH1::SmoothArray(nbins,xx,ntimes);
for (i=0;i<nbins;i++) {
SetBinContent(i+firstbin,xx[i]);
}
delete [] xx;
if (gPad) gPad->Modified();
}
// ------------------------------------------------------------------------
void TH1::StatOverflows(Bool_t flag)
{
// if flag=kTRUE, underflows and overflows are used by the Fill functions
// in the computation of statistics (mean value, RMS).
// By default, underflows or overflows are not used.
fgStatOverflows = flag;
}
//_______________________________________________________________________
void TH1::Streamer(TBuffer &b)
{
// -*-*-*-*-*-*-*Stream a class object*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
// =====================
if (b.IsReading()) {
UInt_t R__s, R__c;
Version_t R__v = b.ReadVersion(&R__s, &R__c);
if (R__v > 2) {
TH1::Class()->ReadBuffer(b, this, R__v, R__s, R__c);
fXaxis.SetParent(this);
fYaxis.SetParent(this);
fZaxis.SetParent(this);
if (fgAddDirectory && !gROOT->ReadingObject()) {
fDirectory = gDirectory;
if (!gDirectory->GetList()->FindObject(this)) gDirectory->Append(this);
}
ResetBit(kCanDelete);
return;
}
//process old versions before automatic schema evolution
TNamed::Streamer(b);
TAttLine::Streamer(b);
TAttFill::Streamer(b);
TAttMarker::Streamer(b);
b >> fNcells;
fXaxis.Streamer(b);
fYaxis.Streamer(b);
fZaxis.Streamer(b);
fXaxis.SetParent(this);
fYaxis.SetParent(this);
fZaxis.SetParent(this);
b >> fBarOffset;
b >> fBarWidth;
b >> fEntries;
b >> fTsumw;
b >> fTsumw2;
b >> fTsumwx;
b >> fTsumwx2;
if (R__v < 2) {
Float_t maximum, minimum, norm;
Float_t *contour=0;
b >> maximum; fMaximum = maximum;
b >> minimum; fMinimum = minimum;
b >> norm; fNormFactor = norm;
Int_t n = b.ReadArray(contour);
fContour.Set(n);
for (Int_t i=0;i<n;i++) fContour.fArray[i] = contour[i];
delete [] contour;
} else {
b >> fMaximum;
b >> fMinimum;
b >> fNormFactor;
fContour.Streamer(b);
}
fSumw2.Streamer(b);
fOption.Streamer(b);
fFunctions->Delete();
fFunctions->Streamer(b);
if (!gROOT->ReadingObject()) {
fDirectory = gDirectory;
if (!gDirectory->GetList()->FindObject(this)) gDirectory->Append(this);
}
b.CheckByteCount(R__s, R__c, TH1::IsA());
} else {
TH1::Class()->WriteBuffer(b,this);
}
}
//______________________________________________________________________________
void TH1::Print(Option_t *option) const
{
// -*-*-*-*-*Print some global quantities for this histogram*-*-*-*-*-*-*-*
// ===============================================
//
// If option "base" is given, number of bins and ranges are also printed
// If option "range" is given, bin contents and errors are also printed
// for all bins in the current range (default 1-->nbins)
// If option "all" is given, bin contents and errors are also printed
// for all bins including under and overflows.
//
printf( "TH1.Print Name = %s, Entries= %d, Total sum= %g\n",GetName(),Int_t(fEntries),GetSumOfWeights());
TString opt = option;
opt.ToLower();
Int_t all;
if (opt.Contains("all")) all = 0;
else if (opt.Contains("range")) all = 1;
else if (opt.Contains("base")) all = 2;
else return;
Int_t bin, binx, biny, binz;
Int_t firstx=0,lastx=0,firsty=0,lasty=0,firstz=0,lastz=0;
if (all == 0) {
lastx = fXaxis.GetNbins()+1;
if (fDimension > 1) lasty = fYaxis.GetNbins()+1;
if (fDimension > 2) lastz = fZaxis.GetNbins()+1;
} else {
firstx = fXaxis.GetFirst(); lastx = fXaxis.GetLast();
if (fDimension > 1) {firsty = fYaxis.GetFirst(); lasty = fYaxis.GetLast();}
if (fDimension > 2) {firstz = fZaxis.GetFirst(); lastz = fZaxis.GetLast();}
}
if (all== 2) {
printf(" Title = %s\n", GetTitle());
printf(" NbinsX= %d, xmin= %g, xmax=%g", fXaxis.GetNbins(), fXaxis.GetXmin(), fXaxis.GetXmax());
if( fDimension > 1) printf(", NbinsY= %d, ymin= %g, ymax=%g", fYaxis.GetNbins(), fYaxis.GetXmin(), fYaxis.GetXmax());
if( fDimension > 2) printf(", NbinsZ= %d, zmin= %g, zmax=%g", fZaxis.GetNbins(), fZaxis.GetXmin(), fZaxis.GetXmax());
printf("\n");
return;
}
Stat_t w,e;
Axis_t x,y,z;
if (fDimension == 1) {
for (binx=firstx;binx<=lastx;binx++) {
x = fXaxis.GetBinCenter(binx);
w = GetBinContent(binx);
e = GetBinError(binx);
if(fSumw2.fN) printf(" fSumw[%d]=%g, x=%g, error=%g\n",binx,w,x,e);
else printf(" fSumw[%d]=%g, x=%g\n",binx,w,x);
}
}
if (fDimension == 2) {
for (biny=firsty;biny<=lasty;biny++) {
y = fYaxis.GetBinCenter(biny);
for (binx=firstx;binx<=lastx;binx++) {
bin = GetBin(binx,biny);
x = fXaxis.GetBinCenter(binx);
w = GetBinContent(bin);
e = GetBinError(bin);
if(fSumw2.fN) printf(" fSumw[%d][%d]=%g, x=%g, y=%g, error=%g\n",binx,biny,w,x,y,e);
else printf(" fSumw[%d][%d]=%g, x=%g, y=%g\n",binx,biny,w,x,y);
}
}
}
if (fDimension == 3) {
for (binz=firstz;binz<=lastz;binz++) {
z = fZaxis.GetBinCenter(binz);
for (biny=firsty;biny<=lasty;biny++) {
y = fYaxis.GetBinCenter(biny);
for (binx=firstx;binx<=lastx;binx++) {
bin = GetBin(binx,biny,binz);
x = fXaxis.GetBinCenter(binx);
w = GetBinContent(bin);
e = GetBinError(bin);
if(fSumw2.fN) printf(" fSumw[%d][%d][%d]=%g, x=%g, y=%g, z=%g, error=%g\n",binx,biny,binz,w,x,y,z,e);
else printf(" fSumw[%d][%d][%d]=%g, x=%g, y=%g, z=%g\n",binx,biny,binz,w,x,y,z);
}
}
}
}
}
//______________________________________________________________________________
void TH1::Rebuild(Option_t *)
{
// Using the current bin info, recompute the arrays for contents and errors
SetBinsLength();
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::Reset(Option_t *option)
{
// -*-*-*-*-*-*Reset this histogram: contents, errors, etc*-*-*-*-*-*-*-*
// ===========================================
//
// if option "ICE" is specified, resets only Integral, Contents and Errors.
TString opt = option;
opt.ToUpper();
fSumw2.Reset();
if (fIntegral) {delete [] fIntegral; fIntegral = 0;}
if (opt.Contains("ICE")) return;
if (fBuffer) BufferEmpty();
fTsumw = 0;
fTsumw2 = 0;
fTsumwx = 0;
fTsumwx2 = 0;
fEntries = 0;
TObject *stats = fFunctions->FindObject("stats");
fFunctions->Remove(stats);
//special logic to support the case where the same object is
//added multiple times in fFunctions.
//This case happens when the same object is added with different
//drawing modes
TObject *obj;
while ((obj = fFunctions->First())) {
while(fFunctions->Remove(obj));
delete obj;
}
if(stats) fFunctions->Add(stats);
fContour.Set(0);
}
//______________________________________________________________________________
void TH1::SavePrimitive(ofstream &out, Option_t *option)
{
// Save primitive as a C++ statement(s) on output stream out
Bool_t nonEqiX = kFALSE;
Bool_t nonEqiY = kFALSE;
Bool_t nonEqiZ = kFALSE;
Int_t i;
// Check if the histogram has equidistant X bins or not. If not, we
// create an array holding the bins.
if (GetXaxis()->GetXbins()->fN && GetXaxis()->GetXbins()->fArray) {
nonEqiX = kTRUE;
out << " Double_t xAxis[" << GetXaxis()->GetXbins()->fN
<< "] = {";
for (i = 0; i < GetXaxis()->GetXbins()->fN; i++) {
if (i != 0) out << ", ";
out << GetXaxis()->GetXbins()->fArray[i];
}
out << "}; " << endl;
}
// If the histogram is 2 or 3 dimensional, check if the histogram
// has equidistant Y bins or not. If not, we create an array
// holding the bins.
if (fDimension > 1 && GetYaxis()->GetXbins()->fN &&
GetYaxis()->GetXbins()->fArray) {
nonEqiY = kTRUE;
out << " Double_t yAxis[" << GetYaxis()->GetXbins()->fN
<< "] = {";
for (i = 0; i < GetYaxis()->GetXbins()->fN; i++) {
if (i != 0) out << ", ";
out << GetYaxis()->GetXbins()->fArray[i];
}
out << "}; " << endl;
}
// IF the histogram is 3 dimensional, check if the histogram
// has equidistant Z bins or not. If not, we create an array
// holding the bins.
if (fDimension > 2 && GetZaxis()->GetXbins()->fN &&
GetZaxis()->GetXbins()->fArray) {
nonEqiZ = kTRUE;
out << " Double_t zAxis[" << GetZaxis()->GetXbins()->fN
<< "] = {";
for (i = 0; i < GetZaxis()->GetXbins()->fN; i++) {
if (i != 0) out << ", ";
out << GetZaxis()->GetXbins()->fArray[i];
}
out << "}; " << endl;
}
char quote = '"';
out <<" "<<endl;
out <<" "<<"TH1"<<" *";
out << GetName() << " = new " << ClassName() << "(" << quote
<< GetName() << quote << "," << quote<< GetTitle() << quote
<< "," << GetXaxis()->GetNbins();
if (nonEqiX)
out << ", xAxis";
else
out << "," << GetXaxis()->GetXmin()
<< "," << GetXaxis()->GetXmax();
if (fDimension > 1) {
out << "," << GetYaxis()->GetNbins();
if (nonEqiY)
out << ", yAxis";
else
out << "," << GetYaxis()->GetXmin()
<< "," << GetYaxis()->GetXmax();
}
if (fDimension > 2) {
out << "," << GetZaxis()->GetNbins();
if (nonEqiZ)
out << ", zAxis";
else
out << "," << GetZaxis()->GetXmin()
<< "," << GetZaxis()->GetXmax();
}
out << ");" << endl;
// save bin contents
Int_t bin;
for (bin=0;bin<fNcells;bin++) {
Double_t bc = GetBinContent(bin);
if (bc) {
out<<" "<<GetName()<<"->SetBinContent("<<bin<<","<<bc<<");"<<endl;
}
}
// save bin errors
if (fSumw2.fN) {
for (bin=0;bin<fNcells;bin++) {
Double_t be = GetBinError(bin);
if (be) {
out<<" "<<GetName()<<"->SetBinError("<<bin<<","<<be<<");"<<endl;
}
}
}
TH1::SavePrimitiveHelp(out, option);
}
//______________________________________________________________________________
void TH1::SavePrimitiveHelp(ofstream &out, Option_t *option)
{
// helper function for the SavePrimitive functions from TH1
// or classes derived from TH1, eg TProfile, TProfile2D.
char quote = '"';
if (TMath::Abs(GetBarOffset()) > 1e-5) {
out<<" "<<GetName()<<"->SetBarOffset("<<GetBarOffset()<<");"<<endl;
}
if (TMath::Abs(GetBarWidth()-1) > 1e-5) {
out<<" "<<GetName()<<"->SetBarWidth("<<GetBarWidth()<<");"<<endl;
}
if (fMinimum != -1111) {
out<<" "<<GetName()<<"->SetMinimum("<<fMinimum<<");"<<endl;
}
if (fMaximum != -1111) {
out<<" "<<GetName()<<"->SetMaximum("<<fMaximum<<");"<<endl;
}
if (fNormFactor != 0) {
out<<" "<<GetName()<<"->SetNormFactor("<<fNormFactor<<");"<<endl;
}
if (fEntries != 0) {
out<<" "<<GetName()<<"->SetEntries("<<fEntries<<");"<<endl;
}
if (fDirectory == 0) {
out<<" "<<GetName()<<"->SetDirectory(0);"<<endl;
}
if (TestBit(kNoStats)) {
out<<" "<<GetName()<<"->SetStats(0);"<<endl;
}
if (fOption.Length() != 0) {
out<<" "<<GetName()<<"->SetOption("<<quote<<fOption.Data()<<quote<<");"<<endl;
}
// save contour levels
Int_t ncontours = GetContour();
if (ncontours > 0) {
out<<" "<<GetName()<<"->SetContour("<<ncontours<<");"<<endl;
for (Int_t bin=0;bin<ncontours;bin++) {
out<<" "<<GetName()<<"->SetContourLevel("<<bin<<","<<GetContourLevel(bin)<<");"<<endl;
}
}
// save list of functions
TObjOptLink *lnk = (TObjOptLink*)fFunctions->FirstLink();
TObject *obj;
while (lnk) {
obj = lnk->GetObject();
obj->SavePrimitive(out,"nodraw");
if (obj->InheritsFrom("TF1")) {
out<<" "<<GetName()<<"->GetListOfFunctions()->Add("<<obj->GetName()<<");"<<endl;
} else if (obj->InheritsFrom("TPaveStats")) {
out<<" "<<GetName()<<"->GetListOfFunctions()->Add(ptstats);"<<endl;
out<<" ptstats->SetParent("<<GetName()<<"->GetListOfFunctions());"<<endl;
} else {
out<<" "<<GetName()<<"->GetListOfFunctions()->Add("<<obj->GetName()<<","<<quote<<lnk->GetOption()<<quote<<");"<<endl;
}
lnk = (TObjOptLink*)lnk->Next();
}
// save attributes
SaveFillAttributes(out,GetName(),0,1001);
SaveLineAttributes(out,GetName(),1,1,1);
SaveMarkerAttributes(out,GetName(),1,1,1);
fXaxis.SaveAttributes(out,GetName(),"->GetXaxis()");
fYaxis.SaveAttributes(out,GetName(),"->GetYaxis()");
fZaxis.SaveAttributes(out,GetName(),"->GetZaxis()");
TString opt = option;
opt.ToLower();
if (!opt.Contains("nodraw")) {
out<<" "<<GetName()<<"->Draw("
<<quote<<option<<quote<<");"<<endl;
}
}
//______________________________________________________________________________
void TH1::UseCurrentStyle()
{
// Copy current attributes from/to current style
if (gStyle->IsReading()) {
fXaxis.ResetAttAxis("X");
fYaxis.ResetAttAxis("Y");
fZaxis.ResetAttAxis("Z");
SetBarOffset(gStyle->GetBarOffset());
SetBarWidth(gStyle->GetBarWidth());
SetFillColor(gStyle->GetHistFillColor());
SetFillStyle(gStyle->GetHistFillStyle());
SetLineColor(gStyle->GetHistLineColor());
SetLineStyle(gStyle->GetHistLineStyle());
SetLineWidth(gStyle->GetHistLineWidth());
SetMarkerColor(gStyle->GetMarkerColor());
SetMarkerStyle(gStyle->GetMarkerStyle());
SetMarkerSize(gStyle->GetMarkerSize());
Int_t dostat = gStyle->GetOptStat();
if (gStyle->GetOptFit() && !dostat) dostat = 1000000001;
SetStats(dostat);
} else {
gStyle->SetBarOffset(fBarOffset);
gStyle->SetBarWidth(fBarWidth);
gStyle->SetHistFillColor(GetFillColor());
gStyle->SetHistFillStyle(GetFillStyle());
gStyle->SetHistLineColor(GetLineColor());
gStyle->SetHistLineStyle(GetLineStyle());
gStyle->SetHistLineWidth(GetLineWidth());
gStyle->SetMarkerColor(GetMarkerColor());
gStyle->SetMarkerStyle(GetMarkerStyle());
gStyle->SetMarkerSize(GetMarkerSize());
gStyle->SetOptStat(TestBit(kNoStats));
}
}
//______________________________________________________________________________
Double_t TH1::GetMean(Int_t axis) const
{
// For axis = 1,2 or 3 returns the mean value of the histogram along
// X,Y or Z axis.
// For axis = 11, 12, 13 returns the standard error of the mean value
// of the histogram along X, Y or Z axis
//
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
// -*-*-*-*-*-*Return mean value of this histogram along the X axis*-*-*-*-*
// ====================================================
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
if (axis<1 || axis>3&&axis<11 || axis>13) return 0;
Stat_t stats[kNstat];
for (Int_t i=4;i<kNstat;i++) stats[i] = 0;
GetStats(stats);
if (stats[0] == 0) return 0;
if (axis<10){
Int_t ax[3] = {2,4,7};
return stats[ax[axis-1]]/stats[0];
} else {
Double_t rms = GetRMS(axis-10);
return (rms/TMath::Sqrt(stats[0]));
}
}
//______________________________________________________________________________
Double_t TH1::GetMeanError(Int_t axis) const
{
// -*-*-*-*-*-*Return standard error of mean of this histogram along the X axis*-*-*-*-*
// ====================================================
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
// Also note, that although the definition of standard error doesn't include the
// assumption of normality, many uses of this feature implicitly assume it.
return GetMean(axis+10);
}
//______________________________________________________________________________
Double_t TH1::GetRMS(Int_t axis) const
{
// For axis = 1,2 or 3 returns the Sigma value of the histogram along
// X, Y or Z axis
// For axis = 11, 12 or 13 returns the error of RMS estimation along
// X, Y or Z axis for Normal distribution
//
// Note that the mean value/sigma is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
// Note that this function returns the Standard Deviation (Sigma)
// of the distribution (not RMS).
// The Sigma estimate is computed as Sqrt((1/N)*(Sum(x_i-x_mean)^2))
// The name "RMS" was introduced many years ago (Hbook/PAW times).
// We kept the name for continuity.
if (axis<1 || axis>3&&axis<11 || axis>13) return 0;
Stat_t x, rms2, stats[kNstat];
for (Int_t i=4;i<kNstat;i++) stats[i] = 0;
GetStats(stats);
if (stats[0] == 0) return 0;
Int_t ax[3] = {2,4,7};
Int_t axm = ax[axis%10 - 1];
x = stats[axm]/stats[0];
rms2 = TMath::Abs(stats[axm+1]/stats[0] -x*x);
if (axis<10)
return TMath::Sqrt(rms2);
else
return TMath::Sqrt(rms2/(2*stats[0]));
}
//______________________________________________________________________________
Double_t TH1::GetRMSError(Int_t axis) const
{
// Return error of RMS estimation for Normal distribution
//
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
// Value returned is standard deviation of sample standard deviation.
return GetRMS(axis+10);
}
//______________________________________________________________________________
Double_t TH1::GetSkewness(Int_t axis) const
{
//For axis = 1, 2 or 3 returns skewness of the histogram along x, y or z axis.
//For axis = 11, 12 or 13 returns the approximate standard error of skewness
//of the histogram along x, y or z axis
//Note, that since third and fourth moment are not calculated
//at the fill time, skewness and its standard error are computed bin by bin
const TAxis *ax;
if (axis==1 || axis==11) ax = &fXaxis;
else if (axis==2 || axis==12) ax = &fYaxis;
else if (axis==3 || axis==13) ax = &fZaxis;
else {
Error("GetSkewness", "illegal value of parameter");
return 0;
}
if (axis < 10) {
//compute skewness
Double_t x, w, mean, rms, rms3, sum=0;
mean = GetMean(axis);
rms = GetRMS(axis);
rms3 = rms*rms*rms;
Int_t bin;
Double_t np=0;
for (bin=ax->GetFirst(); bin<=ax->GetLast(); bin++){
x = GetBinCenter(bin);
w = GetBinContent(bin);
np+=w;
sum+=w*(x-mean)*(x-mean)*(x-mean);
}
sum/=np*rms3;
return sum;
} else {
//compute standard error of skewness
Int_t nbins = ax->GetNbins();
return TMath::Sqrt(6./nbins);
}
}
//______________________________________________________________________________
Double_t TH1::GetKurtosis(Int_t axis) const
{
//For axis =1, 2 or 3 returns kurtosis of the histogram along x, y or z axis.
//Kurtosis(gaussian(0, 1)) = 0.
//For axis =11, 12 or 13 returns the approximate standard error of kurtosis
//of the histogram along x, y or z axis
//Note, that since third and fourth moment are not calculated
//at the fill time, kurtosis and its standard error are computed bin by bin
const TAxis *ax;
if (axis==1 || axis==11) ax = &fXaxis;
else if (axis==2 || axis==12) ax = &fYaxis;
else if (axis==3 || axis==13) ax = &fZaxis;
else {
Error("GetKurtosis", "illegal value of parameter");
return 0;
}
if (axis < 10){
Double_t x, w, mean, rms, rms4, sum=0;
mean = GetMean(axis);
rms = GetRMS(axis);
rms4 = rms*rms*rms*rms;
Int_t bin;
Double_t np=0;
for (bin=ax->GetFirst(); bin<=ax->GetLast(); bin++){
x = GetBinCenter(bin);
w = GetBinContent(bin);
np+=w;
sum+=w*(x-mean)*(x-mean)*(x-mean)*(x-mean);
}
sum/=np*rms4;
return sum-3;
} else {
Int_t nbins = ax->GetNbins();
return TMath::Sqrt(24./nbins);
}
}
//______________________________________________________________________________
void TH1::GetStats(Stat_t *stats) const
{
// fill the array stats from the contents of this histogram
// The array stats must be correctly dimensionned in the calling program.
// stats[0] = sumw
// stats[1] = sumw2
// stats[2] = sumwx
// stats[3] = sumwx2
//
// If no axis-subrange is specified (via TAxis::SetRange), the array stats
// is simply a copy of the statistics quantities computed at filling time.
// If a sub-range is specified, the function recomputes these quantities
// from the bin contents in the current axis range.
//
// Note that the mean value/RMS is computed using the bins in the currently
// defined range (see TAxis::SetRange). By default the range includes
// all bins from 1 to nbins included, excluding underflows and overflows.
// To force the underflows and overflows in the computation, one must
// call the static function TH1::StatOverflows(kTRUE) before filling
// the histogram.
if (fBuffer) ((TH1*)this)->BufferEmpty();
// Loop on bins (possibly including underflows/overflows)
Int_t bin, binx;
Stat_t w,err;
Axis_t x;
if (fTsumw == 0 || fXaxis.TestBit(TAxis::kAxisRange)) {
for (bin=0;bin<4;bin++) stats[bin] = 0;
for (binx=fXaxis.GetFirst();binx<=fXaxis.GetLast();binx++) {
x = fXaxis.GetBinCenter(binx);
w = TMath::Abs(GetBinContent(binx));
err = TMath::Abs(GetBinError(binx));
stats[0] += w;
stats[1] += err*err;
stats[2] += w*x;
stats[3] += w*x*x;
}
} else {
stats[0] = fTsumw;
stats[1] = fTsumw2;
stats[2] = fTsumwx;
stats[3] = fTsumwx2;
}
}
//______________________________________________________________________________
void TH1::PutStats(Stat_t *stats)
{
// Replace current statistics with the values in array stats
fTsumw = stats[0];
fTsumw2 = stats[1];
fTsumwx = stats[2];
fTsumwx2 = stats[3];
}
//______________________________________________________________________________
Stat_t TH1::GetSumOfWeights() const
{
// -*-*-*-*-*-*Return the sum of weights excluding under/overflows*-*-*-*-*
// ===================================================
Int_t bin,binx,biny,binz;
Stat_t sum =0;
for(binz=1; binz<=fZaxis.GetNbins(); binz++) {
for(biny=1; biny<=fYaxis.GetNbins(); biny++) {
for(binx=1; binx<=fXaxis.GetNbins(); binx++) {
bin = GetBin(binx,biny,binz);
sum += GetBinContent(bin);
}
}
}
return sum;
}
//______________________________________________________________________________
Stat_t TH1::Integral(Option_t *option) const
{
//Return integral of bin contents. Only bins in the bins range are considered.
// By default the integral is computed as the sum of bin contents in the range.
// if option "width" is specified, the integral is the sum of
// the bin contents multiplied by the bin width in x.
return Integral(fXaxis.GetFirst(),fXaxis.GetLast(),option);
}
//______________________________________________________________________________
Stat_t TH1::Integral(Int_t binx1, Int_t binx2, Option_t *option) const
{
//Return integral of bin contents between binx1 and binx2 for a 1-D histogram
// By default the integral is computed as the sum of bin contents in the range.
// if option "width" is specified, the integral is the sum of
// the bin contents multiplied by the bin width in x.
if (binx1 < 0) binx1 = 0;
Stat_t integral = 0;
// - Loop on bins in specified range
TString opt = option;
opt.ToLower();
Bool_t width = kFALSE;
if (opt.Contains("width")) width = kTRUE;
Int_t binx;
for (binx=binx1;binx<=binx2;binx++) {
if (width) integral += GetBinContent(binx)*fXaxis.GetBinWidth(binx);
else integral += GetBinContent(binx);
}
return integral;
}
//______________________________________________________________________________
Double_t TH1::KolmogorovTest(const TH1 *h2, Option_t *option) const
{
// Statistical test of compatibility in shape between
// THIS histogram and h2, using Kolmogorov test.
//
// Default: Ignore under- and overflow bins in comparison
//
// option is a character string to specify options
// "U" include Underflows in test (also for 2-dim)
// "O" include Overflows (also valid for 2-dim)
// "N" include comparison of normalizations
// "D" Put out a line of "Debug" printout
// "M" Return the Maximum Kolmogorov distance instead of prob
// "X" Run the pseudo experiments post-processor with the following procedure:
// make pseudoexperiments based on random values from the parent
// distribution and compare the KS distance of the pseudoexperiment
// to the parent distribution. Bin the KS distances in a histogram,
// and then take the integral of all the KS values above the value
// obtained from the original data to Monte Carlo distribution.
// The number of pseudo-experiments nEXPT is currently fixed at 1000.
// The function returns the integral.
// (thanks to Ben Kilminster to submit this procedure). Note that
// this option "X" is much slower.
//
// The returned function value is the probability of test
// (much less than one means NOT compatible)
//
// Code adapted by Rene Brun from original HBOOK routine HDIFF
//
// NOTE1
// A good description of the Kolmogorov test can be seen at:
// http://www.itl.nist.gov/div898/handbook/eda/section3/eda35g.htm
//
// NOTE2
// see also alternative function TH1::Chi2Test
// The Kolmogorov test is assumed to give better results than Chi2Test
// in case of histograms with low statistics.
//
// NOTE3 (Jan Conrad, Fred James)
// "The returned value PROB is calculated such that it will be
// uniformly distributed between zero and one for compatible histograms,
// provided the data are not binned (or the number of bins is very large
// compared with the number of events). Users who have access to unbinned
// data and wish exact confidence levels should therefore not put their data
// into histograms, but should call directly TMath::KolmogorovTest. On
// the other hand, since TH1 is a convenient way of collecting data and
// saving space, this function has been provided. However, the values of
// PROB for binned data will be shifted slightly higher than expected,
// depending on the effects of the binning. For example, when comparing two
// uniform distributions of 500 events in 100 bins, the values of PROB,
// instead of being exactly uniformly distributed between zero and one, have
// a mean value of about 0.56. We can apply a useful
// rule: As long as the bin width is small compared with any significant
// physical effect (for example the experimental resolution) then the binning
// cannot have an important effect. Therefore, we believe that for all
// practical purposes, the probability value PROB is calculated correctly
// provided the user is aware that:
// 1. The value of PROB should not be expected to have exactly the correct
// distribution for binned data.
// 2. The user is responsible for seeing to it that the bin widths are
// small compared with any physical phenomena of interest.
// 3. The effect of binning (if any) is always to make the value of PROB
// slightly too big. That is, setting an acceptance criterion of (PROB>0.05
// will assure that at most 5% of truly compatible histograms are rejected,
// and usually somewhat less."
TString opt = option;
opt.ToUpper();
Double_t prob = 0;
TH1 *h1 = (TH1*)this;
if (h2 == 0) return 0;
TAxis *axis1 = h1->GetXaxis();
TAxis *axis2 = h2->GetXaxis();
Int_t ncx1 = axis1->GetNbins();
Int_t ncx2 = axis2->GetNbins();
// Check consistency of dimensions
if (h1->GetDimension() != 1 || h2->GetDimension() != 1) {
Error("KolmogorovTest","Histograms must be 1-D\n");
return 0;
}
// Check consistency in number of channels
if (ncx1 != ncx2) {
Error("KolmogorovTest","Number of channels is different, %d and %d\n",ncx1,ncx2);
return 0;
}
// Check consistency in channel edges
Double_t difprec = 1e-5;
Double_t diff1 = TMath::Abs(axis1->GetXmin() - axis2->GetXmin());
Double_t diff2 = TMath::Abs(axis1->GetXmax() - axis2->GetXmax());
if (diff1 > difprec || diff2 > difprec) {
Error("KolmogorovTest","histograms with different binning");
return 0;
}
Bool_t afunc1 = kFALSE;
Bool_t afunc2 = kFALSE;
Double_t sum1 = 0, sum2 = 0;
Double_t ew1, ew2, w1 = 0, w2 = 0;
Int_t bin;
for (bin=1;bin<=ncx1;bin++) {
sum1 += h1->GetBinContent(bin);
sum2 += h2->GetBinContent(bin);
ew1 = h1->GetBinError(bin);
ew2 = h2->GetBinError(bin);
w1 += ew1*ew1;
w2 += ew2*ew2;
}
if (sum1 == 0) {
Error("KolmogorovTest","Histogram1 %s integral is zero\n",h1->GetName());
return 0;
}
if (sum2 == 0) {
Error("KolmogorovTest","Histogram2 %s integral is zero\n",h2->GetName());
return 0;
}
Double_t tsum1 = sum1;
Double_t tsum2 = sum2;
if (opt.Contains("U")) {
tsum1 += h1->GetBinContent(0);
tsum2 += h2->GetBinContent(0);
}
if (opt.Contains("O")) {
tsum1 += h1->GetBinContent(ncx1+1);
tsum2 += h2->GetBinContent(ncx1+1);
}
// Check if histograms are weighted.
// If number of entries = number of channels, probably histograms were
// not filled via Fill(), but via SetBinContent()
Double_t ne1 = h1->GetEntries();
Double_t ne2 = h2->GetEntries();
// look at first histogram
Double_t difsum1 = (ne1-tsum1)/tsum1;
Double_t esum1 = sum1;
if (difsum1 > difprec && Int_t(ne1) != ncx1) {
if (opt.Contains("U") || opt.Contains("O")) {
Warning("KolmogorovTest","U/O option with weighted events for hist:%s\n",h1->GetName());
}
if (h1->GetSumw2N() == 0) {
Warning("KolmogorovTest","Weighted events and no Sumw2, hist:%s\n",h1->GetName());
} else {
esum1 = sum1*sum1/w1; //number of equivalent entries
}
}
// look at second histogram
Double_t difsum2 = (ne2-tsum2)/tsum2;
Double_t esum2 = sum2;
if (difsum2 > difprec && Int_t(ne2) != ncx1) {
if (opt.Contains("U") || opt.Contains("O")) {
Warning("KolmogorovTest","U/O option with weighted events for hist:%s\n",h2->GetName());
}
if (h2->GetSumw2N() == 0) {
Warning("KolmogorovTest","Weighted events and no Sumw2, hist:%s\n",h2->GetName());
} else {
esum2 = sum2*sum2/w2; //number of equivalent entries
}
}
Double_t s1 = 1/tsum1;
Double_t s2 = 1/tsum2;
// Find largest difference for Kolmogorov Test
Double_t dfmax =0, rsum1 = 0, rsum2 = 0;
Int_t first = 1;
Int_t last = ncx1;
if (opt.Contains("U")) first = 0;
if (opt.Contains("O")) last = ncx1+1;
for (bin=first;bin<=last;bin++) {
rsum1 += s1*h1->GetBinContent(bin);
rsum2 += s2*h2->GetBinContent(bin);
dfmax = TMath::Max(dfmax,TMath::Abs(rsum1-rsum2));
}
// Get Kolmogorov probability
Double_t z, prb1=0, prb2=0, prb3=0;
if (afunc1) z = dfmax*TMath::Sqrt(esum2);
else if (afunc2) z = dfmax*TMath::Sqrt(esum1);
else z = dfmax*TMath::Sqrt(esum1*esum2/(esum1+esum2));
prob = TMath::KolmogorovProb(z);
if (opt.Contains("N")) {
// Combine probabilities for shape and normalization,
prb1 = prob;
Double_t resum1 = esum1; if (afunc1) resum1 = 0;
Double_t resum2 = esum2; if (afunc2) resum2 = 0;
Double_t d12 = esum1-esum2;
Double_t chi2 = d12*d12/(resum1+resum2);
prb2 = TMath::Prob(chi2,1);
// see Eadie et al., section 11.6.2
if (prob > 0 && prb2 > 0) prob *= prb2*(1-TMath::Log(prob*prb2));
else prob = 0;
}
// X option. Pseudo-experiments post-processor to determine KS probability
const Int_t nEXPT = 1000;
if (opt.Contains("X")) {
Double_t dSEXPT;
Bool_t addStatus = fgAddDirectory;
fgAddDirectory = kFALSE;
TH1F *hDistValues = new TH1F("hDistValues","KS distances",200,0,1);
TH1 *hExpt = (TH1*)Clone();
fgAddDirectory = addStatus;
// make nEXPT experiments (this should be a parameter)
for (Int_t i=0; i < nEXPT; i++) {
hExpt->Reset();
hExpt->FillRandom(h1,(Int_t)ne2);
dSEXPT = KolmogorovTest(hExpt,"M");
hDistValues->Fill(dSEXPT);
}
prb3 = hDistValues->Integral(hDistValues->FindBin(dfmax),200)/hDistValues->Integral();
delete hDistValues;
delete hExpt;
}
// debug printout
if (opt.Contains("D")) {
printf(" Kolmo Prob h1 = %s, sum1=%g\n",h1->GetName(),sum1);
printf(" Kolmo Prob h2 = %s, sum2=%g\n",h2->GetName(),sum2);
printf(" Kolmo Prob = %g, Max Dist = %g\n",prob,dfmax);
if (opt.Contains("N"))
printf(" Kolmo Prob = %f for shape alone, =%f for normalisation alone\n",prb1,prb2);
if (opt.Contains("X"))
printf(" Kolmo Prob = %f with %d pseudo-experiments\n",prb3,nEXPT);
}
// This numerical error condition should never occur:
if (TMath::Abs(rsum1-1) > 0.002) Warning("KolmogorovTest","Numerical problems with h1=%s\n",h1->GetName());
if (TMath::Abs(rsum2-1) > 0.002) Warning("KolmogorovTest","Numerical problems with h2=%s\n",h2->GetName());
if(opt.Contains("M")) return dfmax;
else if(opt.Contains("X")) return prb3;
else return prob;
}
//______________________________________________________________________________
void TH1::SetContent(const Stat_t *content)
{
// -*-*-*-*-*-*Replace bin contents by the contents of array content*-*-*-*
// =====================================================
Int_t bin;
Stat_t bincontent;
for (bin=0; bin<fNcells; bin++) {
bincontent = *(content + bin);
SetBinContent(bin, bincontent);
}
}
//______________________________________________________________________________
Int_t TH1::GetContour(Double_t *levels)
{
// Return contour values into array levels if pointer levels is non zero
//
// The function returns the number of contour levels.
// see GetContourLevel to return one contour only
//
Int_t nlevels = fContour.fN;
if (levels) {
if (nlevels == 0) {
nlevels = 20;
SetContour(nlevels);
} else {
if (TestBit(kUserContour) == 0) SetContour(nlevels);
}
for (Int_t level=0; level<nlevels; level++) levels[level] = fContour.fArray[level];
}
return nlevels;
}
//______________________________________________________________________________
Double_t TH1::GetContourLevel(Int_t level) const
{
// Return value of contour number level
// see GetContour to return the array of all contour levels
if (level <0 || level >= fContour.fN) return 0;
Double_t zlevel = fContour.fArray[level];
return zlevel;
}
//______________________________________________________________________________
Double_t TH1::GetContourLevelPad(Int_t level) const
{
// Return the value of contour number "level" in Pad coordinates ie: if the Pad
// is in log scale along Z it returns le log of the contour level value.
// see GetContour to return the array of all contour levels
if (level <0 || level >= fContour.fN) return 0;
Double_t zlevel = fContour.fArray[level];
// In case of user defined contours and Pad in log scale along Z,
// fContour.fArray doesn't contain the log of the contour whereas it does
// in case of equidistant contours.
if (gPad && gPad->GetLogz() && TestBit(kUserContour)) {
if (zlevel <= 0) return 0;
zlevel = TMath::Log10(zlevel);
}
return zlevel;
}
//______________________________________________________________________________
void TH1::SetBuffer(Int_t buffersize, Option_t * /*option*/)
{
// set the maximum number of entries to be kept in the buffer
if (fBuffer) {
BufferEmpty();
delete [] fBuffer;
fBuffer = 0;
}
if (buffersize <= 0) {
fBufferSize = 0;
return;
}
if (buffersize < 100) buffersize = 100;
fBufferSize = 1 + buffersize*(fDimension+1);
fBuffer = new Double_t[fBufferSize];
memset(fBuffer,0,8*fBufferSize);
}
//______________________________________________________________________________
void TH1::SetContour(Int_t nlevels, const Double_t *levels)
{
// -*-*-*-*-*-*Set the number and values of contour levels*-*-*-*-*-*-*-*-*
// ===========================================
//
// By default the number of contour levels is set to 20.
//
// if argument levels = 0 or missing, equidistant contours are computed
//
Int_t level;
ResetBit(kUserContour);
if (nlevels <=0 ) {
fContour.Set(0);
return;
}
fContour.Set(nlevels);
// - Contour levels are specified
if (levels) {
SetBit(kUserContour);
for (level=0; level<nlevels; level++) fContour.fArray[level] = levels[level];
} else {
// - contour levels are computed automatically as equidistant contours
Double_t zmin = GetMinimum();
Double_t zmax = GetMaximum();
if ((zmin == zmax) && (zmin != 0)) {
zmax += 0.01*TMath::Abs(zmax);
zmin -= 0.01*TMath::Abs(zmin);
}
Double_t dz = (zmax-zmin)/Double_t(nlevels);
if (gPad && gPad->GetLogz()) {
if (zmax <= 0) return;
if (zmin <= 0) zmin = 0.001*zmax;
zmin = TMath::Log10(zmin);
zmax = TMath::Log10(zmax);
dz = (zmax-zmin)/Double_t(nlevels);
}
for (level=0; level<nlevels; level++) {
fContour.fArray[level] = zmin + dz*Double_t(level);
}
}
}
//______________________________________________________________________________
void TH1::SetContourLevel(Int_t level, Double_t value)
{
// -*-*-*-*-*-*-*-*-*Set value for one contour level*-*-*-*-*-*-*-*-*-*-*-*
// ===============================
if (level <0 || level >= fContour.fN) return;
SetBit(kUserContour);
fContour.fArray[level] = value;
}
//______________________________________________________________________________
Double_t TH1::GetMaximum(Double_t maxval) const
{
// Return maximum value smaller than maxval of bins in the range*-*-*-*-*-*
if (fMaximum != -1111) return fMaximum;
Int_t bin, binx, biny, binz;
Int_t xfirst = fXaxis.GetFirst();
Int_t xlast = fXaxis.GetLast();
Int_t yfirst = fYaxis.GetFirst();
Int_t ylast = fYaxis.GetLast();
Int_t zfirst = fZaxis.GetFirst();
Int_t zlast = fZaxis.GetLast();
Double_t maximum = -FLT_MAX, value;
for (binz=zfirst;binz<=zlast;binz++) {
for (biny=yfirst;biny<=ylast;biny++) {
for (binx=xfirst;binx<=xlast;binx++) {
bin = GetBin(binx,biny,binz);
value = GetBinContent(bin);
if (value > maximum && value < maxval) maximum = value;
}
}
}
return maximum;
}
//______________________________________________________________________________
Int_t TH1::GetMaximumBin() const
{
// -*-*-*-*-*Return location of bin with maximum value in the range*-*
// ======================================================
Int_t locmax, locmay, locmaz;
return GetMaximumBin(locmax, locmay, locmaz);
}
//______________________________________________________________________________
Int_t TH1::GetMaximumBin(Int_t &locmax, Int_t &locmay, Int_t &locmaz) const
{
// -*-*-*-*-*Return location of bin with maximum value in the range*-*
// ======================================================
Int_t bin, binx, biny, binz;
Int_t locm;
Int_t xfirst = fXaxis.GetFirst();
Int_t xlast = fXaxis.GetLast();
Int_t yfirst = fYaxis.GetFirst();
Int_t ylast = fYaxis.GetLast();
Int_t zfirst = fZaxis.GetFirst();
Int_t zlast = fZaxis.GetLast();
Double_t maximum = -FLT_MAX, value;
locm = locmax = locmay = locmaz = 0;
for (binz=zfirst;binz<=zlast;binz++) {
for (biny=yfirst;biny<=ylast;biny++) {
for (binx=xfirst;binx<=xlast;binx++) {
bin = GetBin(binx,biny,binz);
value = GetBinContent(bin);
if (value > maximum) {
maximum = value;
locm = bin;
locmax = binx;
locmay = biny;
locmaz = binz;
}
}
}
}
return locm;
}
//______________________________________________________________________________
Double_t TH1::GetMinimum(Double_t minval) const
{
// Return minimum value greater than minval of bins in the range
if (fMinimum != -1111) return fMinimum;
Int_t bin, binx, biny, binz;
Int_t xfirst = fXaxis.GetFirst();
Int_t xlast = fXaxis.GetLast();
Int_t yfirst = fYaxis.GetFirst();
Int_t ylast = fYaxis.GetLast();
Int_t zfirst = fZaxis.GetFirst();
Int_t zlast = fZaxis.GetLast();
Double_t minimum=FLT_MAX, value;
for (binz=zfirst;binz<=zlast;binz++) {
for (biny=yfirst;biny<=ylast;biny++) {
for (binx=xfirst;binx<=xlast;binx++) {
bin = GetBin(binx,biny,binz);
value = GetBinContent(bin);
if (value < minimum && value > minval) minimum = value;
}
}
}
return minimum;
}
//______________________________________________________________________________
Int_t TH1::GetMinimumBin() const
{
// -*-*-*-*-*Return location of bin with minimum value in the range*-*
// ======================================================
Int_t locmix, locmiy, locmiz;
return GetMinimumBin(locmix, locmiy, locmiz);
}
//______________________________________________________________________________
Int_t TH1::GetMinimumBin(Int_t &locmix, Int_t &locmiy, Int_t &locmiz) const
{
// -*-*-*-*-*Return location of bin with minimum value in the range*-*
// ======================================================
Int_t bin, binx, biny, binz;
Int_t locm;
Int_t xfirst = fXaxis.GetFirst();
Int_t xlast = fXaxis.GetLast();
Int_t yfirst = fYaxis.GetFirst();
Int_t ylast = fYaxis.GetLast();
Int_t zfirst = fZaxis.GetFirst();
Int_t zlast = fZaxis.GetLast();
Double_t minimum = FLT_MAX, value;
locm = locmix = locmiy = locmiz = 0;
for (binz=zfirst;binz<=zlast;binz++) {
for (biny=yfirst;biny<=ylast;biny++) {
for (binx=xfirst;binx<=xlast;binx++) {
bin = GetBin(binx,biny,binz);
value = GetBinContent(bin);
if (value < minimum) {
minimum = value;
locm = bin;
locmix = binx;
locmiy = biny;
locmiz = binz;
}
}
}
}
return locm;
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, Axis_t xmin, Axis_t xmax)
{
// -*-*-*-*-*-*-*Redefine x axis parameters*-*-*-*-*-*-*-*-*-*-*-*
// ===========================
// The X axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
if (GetDimension() != 1) {
Error("SetBins","Operation only valid for 1-d histograms");
return;
}
fXaxis.SetRange(0,0);
fXaxis.Set(nx,xmin,xmax);
fYaxis.Set(1,0,1);
fZaxis.Set(1,0,1);
fNcells = nx+2;
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, const Axis_t *xBins)
{
// -*-*-*-*-*-*-*Redefine x axis parameters with variable bin sizes *-*-*-*-*-*-*-*-*-*
// ===================================================
// The X axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
// xBins is supposed to be of length nx+1
if (GetDimension() != 1) {
Error("SetBins","Operation only valid for 1-d histograms");
return;
}
fXaxis.SetRange(0,0);
fXaxis.Set(nx,xBins);
fYaxis.Set(1,0,1);
fZaxis.Set(1,0,1);
fNcells = nx+2;
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, Axis_t xmin, Axis_t xmax, Int_t ny, Axis_t ymin, Axis_t ymax)
{
// -*-*-*-*-*-*-*Redefine x and y axis parameters*-*-*-*-*-*-*-*-*-*-*-*
// =================================
// The X and Y axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
if (GetDimension() != 2) {
Error("SetBins","Operation only valid for 2-d histograms");
return;
}
fXaxis.SetRange(0,0);
fYaxis.SetRange(0,0);
fXaxis.Set(nx,xmin,xmax);
fYaxis.Set(ny,ymin,ymax);
fZaxis.Set(1,0,1);
fNcells = (nx+2)*(ny+2);
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, const Axis_t *xBins, Int_t ny, const Axis_t *yBins)
{
// -*-*-*-*-*-*-*Redefine x and y axis parameters with variable bin sizes *-*-*-*-*-*-*-*-*
// =========================================================
// The X and Y axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
// xBins is supposed to be of length nx+1, yBins is supposed to be of length ny+1
if (GetDimension() != 2) {
Error("SetBins","Operation only valid for 2-d histograms");
return;
}
fXaxis.SetRange(0,0);
fYaxis.SetRange(0,0);
fXaxis.Set(nx,xBins);
fYaxis.Set(ny,yBins);
fZaxis.Set(1,0,1);
fNcells = (nx+2)*(ny+2);
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetBins(Int_t nx, Axis_t xmin, Axis_t xmax, Int_t ny, Axis_t ymin, Axis_t ymax, Int_t nz, Axis_t zmin, Axis_t zmax)
{
// -*-*-*-*-*-*-*Redefine x, y and z axis parameters*-*-*-*-*-*-*-*-*-*-*-*
// ====================================
// The X, Y and Z axis parameters are modified.
// The bins content array is resized
// if errors (Sumw2) the errors array is resized
// The previous bin contents are lost
// To change only the axis limits, see TAxis::SetRange
if (GetDimension() != 3) {
Error("SetBins","Operation only valid for 3-d histograms");
return;
}
fXaxis.SetRange(0,0);
fYaxis.SetRange(0,0);
fZaxis.SetRange(0,0);
fXaxis.Set(nx,xmin,xmax);
fYaxis.Set(ny,ymin,ymax);
fZaxis.Set(nz,zmin,zmax);
fNcells = (nx+2)*(ny+2)*(nz+2);
SetBinsLength(fNcells);
if (fSumw2.fN) {
fSumw2.Set(fNcells);
}
}
//______________________________________________________________________________
void TH1::SetMaximum(Double_t maximum)
{
// -*-*-*-*-*-*-*Set the maximum value for the Y axis*-*-*-*-*-*-*-*-*-*-*-*
// ====================================
// By default the maximum value is automatically set to the maximum
// bin content plus a margin of 10 per cent.
// Use TH1::GetMaximum to find the maximum value of an histogram
// Use TH1::GetMaximumBin to find the bin with the maximum value of an histogram
//
fMaximum = maximum;
}
//______________________________________________________________________________
void TH1::SetMinimum(Double_t minimum)
{
// -*-*-*-*-*-*-*Set the minimum value for the Y axis*-*-*-*-*-*-*-*-*-*-*-*
// ====================================
// By default the minimum value is automatically set to zero if all bin contents
// are positive or the minimum - 10 per cent otherwise.
// Use TH1::GetMinimum to find the minimum value of an histogram
// Use TH1::GetMinimumBin to find the bin with the minimum value of an histogram
//
fMinimum = minimum;
}
//______________________________________________________________________________
void TH1::SetDirectory(TDirectory *dir)
{
// By default when an histogram is created, it is added to the list
// of histogram objects in the current directory in memory.
// Remove reference to this histogram from current directory and add
// reference to new directory dir. dir can be 0 in which case the
// histogram does not belong to any directory.
if (fDirectory == dir) return;
if (fDirectory) fDirectory->GetList()->Remove(this);
fDirectory = dir;
if (fDirectory) fDirectory->GetList()->Add(this);
}
//______________________________________________________________________________
void TH1::SetError(const Stat_t *error)
{
// -*-*-*-*-*-*-*Replace bin errors by values in array error*-*-*-*-*-*-*-*-*
// ===========================================
Int_t bin;
Stat_t binerror;
for (bin=0; bin<fNcells; bin++) {
binerror = error[bin];
SetBinError(bin, binerror);
}
}
//______________________________________________________________________________
void TH1::SetName(const char *name)
{
// Change the name of this histogram
//
// Histograms are named objects in a THashList.
// We must update the hashlist if we change the name
if (fDirectory) fDirectory->GetList()->Remove(this);
fName = name;
if (fDirectory) fDirectory->GetList()->Add(this);
}
//______________________________________________________________________________
void TH1::SetNameTitle(const char *name, const char *title)
{
// Change the name and title of this histogram
//
// Histograms are named objects in a THashList.
// We must update the hashlist if we change the name
if (fDirectory) fDirectory->GetList()->Remove(this);
fName = name;
SetTitle(title);
if (fDirectory) fDirectory->GetList()->Add(this);
}
//______________________________________________________________________________
void TH1::SetStats(Bool_t stats)
{
// -*-*-*-*-*-*-*Set statistics option on/off
// ============================
// By default, the statistics box is drawn.
// The paint options can be selected via gStyle->SetOptStats.
// This function sets/resets the kNoStats bin in the histogram object.
// It has priority over the Style option.
ResetBit(kNoStats);
if (!stats) {
SetBit(kNoStats);
//remove the "stats" object from the list of functions
if (fFunctions) delete fFunctions->FindObject("stats");
}
}
//______________________________________________________________________________
void TH1::Sumw2()
{
// -*-*-*Create structure to store sum of squares of weights*-*-*-*-*-*-*-*
// ===================================================
//
// if histogram is already filled, the sum of squares of weights
// is filled with the existing bin contents
//
// The error per bin will be computed as sqrt(sum of squares of weight)
// for each bin.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (fSumw2.fN) {
Warning("Sumw2","Sum of squares of weights structure already created");
return;
}
fSumw2.Set(fNcells);
for (Int_t bin=0; bin<fNcells; bin++) {
fSumw2.fArray[bin] = GetBinContent(bin);
}
}
//______________________________________________________________________________
TF1 *TH1::GetFunction(const char *name) const
{
// -*-*-*Return pointer to function with name*-*-*-*-*-*-*-*-*-*-*-*-*
// ===================================
//
// Functions such as TH1::Fit store the fitted function in the list of
// functions of this histogram.
return (TF1*)fFunctions->FindObject(name);
}
//______________________________________________________________________________
Stat_t TH1::GetBinError(Int_t bin) const
{
// -*-*-*-*-*Return value of error associated to bin number bin*-*-*-*-*
// ==================================================
//
// if the sum of squares of weights has been defined (via Sumw2),
// this function returns the sqrt(sum of w2).
// otherwise it returns the sqrt(contents) for this bin.
//
// -*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (fBuffer) ((TH1*)this)->BufferEmpty();
if (fSumw2.fN) return TMath::Sqrt(fSumw2.fArray[bin]);
Stat_t error2 = TMath::Abs(GetBinContent(bin));
return TMath::Sqrt(error2);
}
//______________________________________________________________________________
Stat_t TH1::GetBinError(Int_t binx, Int_t biny) const
{
// -*-*-*-*-*Return error of bin number binx, biny
// =====================================
// NB: Function to be called for 2-d histograms only
Int_t bin = GetBin(binx,biny);
return GetBinError(bin);
}
//______________________________________________________________________________
Stat_t TH1::GetBinError(Int_t binx, Int_t biny, Int_t binz) const
{
// -*-*-*-*-*Return error of bin number binx,biny,binz
// =========================================
// NB: Function to be called for 3-d histograms only
Int_t bin = GetBin(binx,biny,binz);
return GetBinError(bin);
}
//______________________________________________________________________________
Stat_t TH1::GetCellContent(Int_t binx, Int_t biny) const
{
// -*-*-*-*-*Return content of bin number binx, biny
// =====================================
// NB: Function to be called for 2-d histograms only
Int_t bin = GetBin(binx,biny);
return GetBinContent(bin);
}
//______________________________________________________________________________
Stat_t TH1::GetCellError(Int_t binx, Int_t biny) const
{
// -*-*-*-*-*Return error of bin number binx, biny
// =====================================
// NB: Function to be called for 2-d histograms only
Int_t bin = GetBin(binx,biny);
return GetBinError(bin);
}
//______________________________________________________________________________
void TH1::SetBinError(Int_t bin, Stat_t error)
{
// see convention for numbering bins in TH1::GetBin
if (!fSumw2.fN) Sumw2();
if (bin <0 || bin>= fSumw2.fN) return;
fSumw2.fArray[bin] = error*error;
}
//______________________________________________________________________________
void TH1::SetBinContent(Int_t binx, Int_t biny, Stat_t content)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
SetBinContent(biny*(fXaxis.GetNbins()+2) + binx,content);
}
//______________________________________________________________________________
void TH1::SetBinContent(Int_t binx, Int_t biny, Int_t binz, Stat_t content)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
if (binz <0 || binz>fZaxis.GetNbins()+1) return;
Int_t bin = GetBin(binx,biny,binz);
SetBinContent(bin,content);
}
//______________________________________________________________________________
void TH1::SetCellContent(Int_t binx, Int_t biny, Stat_t content)
{
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
SetBinContent(biny*(fXaxis.GetNbins()+2) + binx,content);
}
//______________________________________________________________________________
void TH1::SetBinError(Int_t binx, Int_t biny, Stat_t error)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
SetBinError(biny*(fXaxis.GetNbins()+2) + binx,error);
}
//______________________________________________________________________________
void TH1::SetBinError(Int_t binx, Int_t biny, Int_t binz, Stat_t error)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
if (binz <0 || binz>fZaxis.GetNbins()+1) return;
Int_t bin = GetBin(binx,biny,binz);
SetBinError(bin,error);
}
//______________________________________________________________________________
void TH1::SetCellError(Int_t binx, Int_t biny, Stat_t error)
{
// see convention for numbering bins in TH1::GetBin
if (binx <0 || binx>fXaxis.GetNbins()+1) return;
if (biny <0 || biny>fYaxis.GetNbins()+1) return;
if (!fSumw2.fN) Sumw2();
Int_t bin = biny*(fXaxis.GetNbins()+2) + binx;
fSumw2.fArray[bin] = error*error;
}
//______________________________________________________________________________
void TH1::SetBinContent(Int_t, Stat_t)
{
// see convention for numbering bins in TH1::GetBin
AbstractMethod("SetBinContent");
}
ClassImp(TH1C)
//______________________________________________________________________________
// TH1C methods
//______________________________________________________________________________
TH1C::TH1C(): TH1(), TArrayC()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1C::TH1C(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type char (one byte per channel)
// ==========================================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayC::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1C::TH1C(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type char (one byte per channel)
// ==========================================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayC::Set(fNcells);
}
//______________________________________________________________________________
TH1C::TH1C(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type char (one byte per channel)
// ==========================================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayC::Set(fNcells);
}
//______________________________________________________________________________
TH1C::~TH1C()
{
}
//______________________________________________________________________________
TH1C::TH1C(const TH1C &h1c) : TH1(), TArrayC()
{
((TH1C&)h1c).Copy(*this);
}
//______________________________________________________________________________
void TH1C::AddBinContent(Int_t bin)
{
// -*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
if (fArray[bin] < 127) fArray[bin]++;
}
//______________________________________________________________________________
void TH1C::AddBinContent(Int_t bin, Stat_t w)
{
// -*-*-*-*-*-*-*-*Increment bin content by w*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
Int_t newval = fArray[bin] + Int_t(w);
if (newval > -128 && newval < 128) {fArray[bin] = Char_t(newval); return;}
if (newval < -127) fArray[bin] = -127;
if (newval > 127) fArray[bin] = 127;
}
//______________________________________________________________________________
void TH1C::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayC::Copy((TH1C&)newth1);
}
//______________________________________________________________________________
TH1 *TH1C::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1C *newth1 = (TH1C*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1C::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1C*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1C::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayC::Reset();
}
//______________________________________________________________________________
void TH1C::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = Char_t (content);
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = Char_t (content);
fEntries++;
}
//______________________________________________________________________________
void TH1C::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayC::Set(n);
}
//______________________________________________________________________________
TH1C& TH1C::operator=(const TH1C &h1)
{
if (this != &h1) ((TH1C&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1C operator*(Double_t c1, const TH1C &h1)
{
TH1C hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1C operator+(const TH1C &h1, const TH1C &h2)
{
TH1C hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1C operator-(const TH1C &h1, const TH1C &h2)
{
TH1C hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1C operator*(const TH1C &h1, const TH1C &h2)
{
TH1C hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1C operator/(const TH1C &h1, const TH1C &h2)
{
TH1C hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
ClassImp(TH1S)
//______________________________________________________________________________
// TH1S methods
//______________________________________________________________________________
TH1S::TH1S(): TH1(), TArrayS()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1S::TH1S(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type short
// ====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayS::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1S::TH1S(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type short
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayS::Set(fNcells);
}
//______________________________________________________________________________
TH1S::TH1S(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type short
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayS::Set(fNcells);
}
//______________________________________________________________________________
TH1S::~TH1S()
{
}
//______________________________________________________________________________
TH1S::TH1S(const TH1S &h1s) : TH1(), TArrayS()
{
((TH1S&)h1s).Copy(*this);
}
//______________________________________________________________________________
void TH1S::AddBinContent(Int_t bin)
{
// -*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
if (fArray[bin] < 32767) fArray[bin]++;
}
//______________________________________________________________________________
void TH1S::AddBinContent(Int_t bin, Stat_t w)
{
// Increment bin content by w
// ==========================
Int_t newval = fArray[bin] + Int_t(w);
if (newval > -32768 && newval < 32768) {fArray[bin] = Short_t(newval); return;}
if (newval < -32767) fArray[bin] = -32767;
if (newval > 32767) fArray[bin] = 32767;
}
//______________________________________________________________________________
void TH1S::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayS::Copy((TH1S&)newth1);
}
//______________________________________________________________________________
TH1 *TH1S::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1S *newth1 = (TH1S*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1S::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1S*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1S::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayS::Reset();
}
//______________________________________________________________________________
void TH1S::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = Short_t (content);
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = Short_t (content);
fEntries++;
}
//______________________________________________________________________________
void TH1S::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayS::Set(n);
}
//______________________________________________________________________________
TH1S& TH1S::operator=(const TH1S &h1)
{
if (this != &h1) ((TH1S&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1S operator*(Double_t c1, const TH1S &h1)
{
TH1S hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1S operator+(const TH1S &h1, const TH1S &h2)
{
TH1S hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1S operator-(const TH1S &h1, const TH1S &h2)
{
TH1S hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1S operator*(const TH1S &h1, const TH1S &h2)
{
TH1S hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1S operator/(const TH1S &h1, const TH1S &h2)
{
TH1S hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
ClassImp(TH1I)
//______________________________________________________________________________
// TH1I methods
//______________________________________________________________________________
TH1I::TH1I(): TH1(), TArrayI()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1I::TH1I(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type integer
// ====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayI::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1I::TH1I(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type integer
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayI::Set(fNcells);
}
//______________________________________________________________________________
TH1I::TH1I(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type integer
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayI::Set(fNcells);
}
//______________________________________________________________________________
TH1I::~TH1I()
{
}
//______________________________________________________________________________
TH1I::TH1I(const TH1I &h1i) : TH1(), TArrayI()
{
((TH1I&)h1i).Copy(*this);
}
//______________________________________________________________________________
void TH1I::AddBinContent(Int_t bin)
{
// -*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
// ==========================
if (fArray[bin] < 2147483647) fArray[bin]++;
}
//______________________________________________________________________________
void TH1I::AddBinContent(Int_t bin, Stat_t w)
{
// Increment bin content by w
// ==========================
Int_t newval = fArray[bin] + Int_t(w);
if (newval > -2147483647 && newval < 2147483647) {fArray[bin] = Int_t(newval); return;}
if (newval < -2147483647) fArray[bin] = -2147483647;
if (newval > 2147483647) fArray[bin] = 2147483647;
}
//______________________________________________________________________________
void TH1I::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayI::Copy((TH1I&)newth1);
}
//______________________________________________________________________________
TH1 *TH1I::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1I *newth1 = (TH1I*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1I::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1I*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1I::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayI::Reset();
}
//______________________________________________________________________________
void TH1I::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = Int_t (content);
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = Int_t (content);
fEntries++;
}
//______________________________________________________________________________
void TH1I::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayI::Set(n);
}
//______________________________________________________________________________
TH1I& TH1I::operator=(const TH1I &h1)
{
if (this != &h1) ((TH1I&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1I operator*(Double_t c1, const TH1I &h1)
{
TH1I hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1I operator+(const TH1I &h1, const TH1I &h2)
{
TH1I hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1I operator-(const TH1I &h1, const TH1I &h2)
{
TH1I hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1I operator*(const TH1I &h1, const TH1I &h2)
{
TH1I hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1I operator/(const TH1I &h1, const TH1I &h2)
{
TH1I hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
ClassImp(TH1F)
//______________________________________________________________________________
// TH1F methods
//______________________________________________________________________________
TH1F::TH1F(): TH1(), TArrayF()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1F::TH1F(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type float
// ====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayF::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1F::TH1F(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type float
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayF::Set(fNcells);
}
//______________________________________________________________________________
TH1F::TH1F(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type float
// =========================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayF::Set(fNcells);
}
//______________________________________________________________________________
TH1F::TH1F(const TVectorF &v)
: TH1("TVectorF","",v.GetNrows(),0,v.GetNrows())
{
// Create a histogram from a TVectorF
// by default the histogram name is "TVectorF" and title = ""
TArrayF::Set(fNcells);
fDimension = 1;
for (Int_t i=0;i<v.GetNrows();i++) {
SetBinContent(i+1,v(i));
}
TArrayF::Set(fNcells);
}
//______________________________________________________________________________
TH1F::TH1F(const TH1F &h) : TH1(), TArrayF()
{
((TH1F&)h).Copy(*this);
}
//______________________________________________________________________________
TH1F::~TH1F()
{
}
//______________________________________________________________________________
void TH1F::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayF::Copy((TH1F&)newth1);
}
//______________________________________________________________________________
TH1 *TH1F::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1F *newth1 = (TH1F*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1F::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1F*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1F::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayF::Reset();
}
//______________________________________________________________________________
void TH1F::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = Float_t (content);
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = Float_t (content);
fEntries++;
}
//______________________________________________________________________________
void TH1F::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayF::Set(n);
}
//______________________________________________________________________________
TH1F& TH1F::operator=(const TH1F &h1)
{
if (this != &h1) ((TH1F&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1F operator*(Double_t c1, const TH1F &h1)
{
TH1F hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1F operator+(const TH1F &h1, const TH1F &h2)
{
TH1F hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1F operator-(const TH1F &h1, const TH1F &h2)
{
TH1F hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1F operator*(const TH1F &h1, const TH1F &h2)
{
TH1F hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1F operator/(const TH1F &h1, const TH1F &h2)
{
TH1F hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
ClassImp(TH1D)
//______________________________________________________________________________
// TH1D methods
//______________________________________________________________________________
TH1D::TH1D(): TH1(), TArrayD()
{
fDimension = 1;
SetBinsLength(3);
}
//______________________________________________________________________________
TH1D::TH1D(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
: TH1(name,title,nbins,xlow,xup)
{
//
// Create a 1-Dim histogram with fix bins of type double
// =====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayD::Set(fNcells);
if (xlow >= xup) SetBuffer(fgBufferSize);
}
//______________________________________________________________________________
TH1D::TH1D(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type double
// =====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayD::Set(fNcells);
}
//______________________________________________________________________________
TH1D::TH1D(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
: TH1(name,title,nbins,xbins)
{
//
// Create a 1-Dim histogram with variable bins of type double
// =====================================================
// (see TH1::TH1 for explanation of parameters)
//
fDimension = 1;
TArrayD::Set(fNcells);
}
//______________________________________________________________________________
TH1D::TH1D(const TVectorD &v)
: TH1("TVectorD","",v.GetNrows(),0,v.GetNrows())
{
// Create a histogram from a TVectorD
// by default the histogram name is "TVectorD" and title = ""
TArrayD::Set(fNcells);
fDimension = 1;
for (Int_t i=0;i<v.GetNrows();i++) {
SetBinContent(i+1,v(i));
}
TArrayD::Set(fNcells);
}
//______________________________________________________________________________
TH1D::~TH1D()
{
}
//______________________________________________________________________________
TH1D::TH1D(const TH1D &h1d) : TH1(), TArrayD()
{
((TH1D&)h1d).Copy(*this);
}
//______________________________________________________________________________
void TH1D::Copy(TObject &newth1) const
{
TH1::Copy(newth1);
TArrayD::Copy((TH1D&)newth1);
}
//______________________________________________________________________________
TH1 *TH1D::DrawCopy(Option_t *option) const
{
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
TH1D *newth1 = (TH1D*)Clone();
newth1->SetDirectory(0);
newth1->SetBit(kCanDelete);
newth1->AppendPad(opt.Data());
return newth1;
}
//______________________________________________________________________________
Stat_t TH1D::GetBinContent(Int_t bin) const
{
// see convention for numbering bins in TH1::GetBin
if (fBuffer) ((TH1D*)this)->BufferEmpty();
if (bin < 0) bin = 0;
if (bin >= fNcells) bin = fNcells-1;
if (!fArray) return 0;
return Stat_t (fArray[bin]);
}
//______________________________________________________________________________
void TH1D::Reset(Option_t *option)
{
TH1::Reset(option);
TArrayD::Reset();
}
//______________________________________________________________________________
void TH1D::SetBinContent(Int_t bin, Stat_t content)
{
// Set bin content
// see convention for numbering bins in TH1::GetBin
// In case the bin number is greater than the number of bins and
// the timedisplay option is set or the kCanRebin bit is set,
// the number of bins is automatically doubled to accomodate the new bin
if (bin < 0) return;
if (bin >= fNcells-1) {
if (!fXaxis.GetTimeDisplay() && !TestBit(kCanRebin)) {
if (bin == fNcells-1) fArray[bin] = content;
return;
}
while (bin >= fNcells-1) LabelsInflate();
}
fArray[bin] = content;
fEntries++;
}
//______________________________________________________________________________
void TH1D::SetBinsLength(Int_t n)
{
// Set total number of bins including under/overflow
// Reallocate bin contents array
if (n < 0) n = fXaxis.GetNbins() + 2;
fNcells = n;
TArrayD::Set(n);
}
//______________________________________________________________________________
TH1D& TH1D::operator=(const TH1D &h1)
{
if (this != &h1) ((TH1D&)h1).Copy(*this);
return *this;
}
//______________________________________________________________________________
TH1D operator*(Double_t c1, const TH1D &h1)
{
TH1D hnew = h1;
hnew.Scale(c1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1D operator+(const TH1D &h1, const TH1D &h2)
{
TH1D hnew = h1;
hnew.Add(&h2,1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1D operator-(const TH1D &h1, const TH1D &h2)
{
TH1D hnew = h1;
hnew.Add(&h2,-1);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1D operator*(const TH1D &h1, const TH1D &h2)
{
TH1D hnew = h1;
hnew.Multiply(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1D operator/(const TH1D &h1, const TH1D &h2)
{
TH1D hnew = h1;
hnew.Divide(&h2);
hnew.SetDirectory(0);
return hnew;
}
//______________________________________________________________________________
TH1 *R__H(Int_t hid)
{
//return pointer to histogram with name
// hid if id >=0
// h_id if id <0
char hname[20];
if(hid >= 0) sprintf(hname,"h%d",hid);
else sprintf(hname,"h_%d",hid);
return (TH1*)gDirectory->Get(hname);
}
//______________________________________________________________________________
TH1 *R__H(const char * hname)
{
//return pointer to histogram with name hname
return (TH1*)gDirectory->Get(hname);
}