// @(#)root/hist:$Name: $:$Id: TGraph2D.cxx,v 1.00
// Author: Olivier Couet
/*************************************************************************
* Copyright (C) 1995-2000, Rene Brun and Fons Rademakers. *
* All rights reserved. *
* *
* For the licensing terms see $ROOTSYS/LICENSE. *
* For the list of contributors see $ROOTSYS/README/CREDITS. *
*************************************************************************/
#include "Riostream.h"
#include "TROOT.h"
#include "TMath.h"
#include "TGraph2D.h"
#include "TGraphDelaunay.h"
#include "TVirtualPad.h"
#include "TVirtualFitter.h"
ClassImp(TGraph2D)
//______________________________________________________________________________
//
// A Graph2D is a graphics object made of three arrays X, Y and Z with the same
// number of points each.
//
// This class has different constructors:
//
// 1) With an array's dimension and three arrays x, y, and z:
//
// TGraph2D *g = new TGraph2D(n, x, y, z);
//
// x, y, z arrays can be doubles, floats, or ints.
//
// 2) With an array's dimension only:
//
// TGraph2D *g = new TGraph2D(n);
//
// The internal arrays are then filled with SetPoint. The following line
// fills the the internal arrays at the position "i" with the values x,y,z.
//
// g->SetPoint(i, x, y, z);
//
// 3) Without parameters:
//
// TGraph2D *g = new TGraph2D();
//
// again SetPoint must be used to fill the internal arrays.
//
// 4) From a file:
//
// TGraph2D *g = new TGraph2D("graph.dat");
//
// Arrays are read from the ASCII file "graph.dat" according to a specifies
// format. The format's default value is "%lg %lg %lg"
//
// Note that in any of these three cases, SetPoint can be used to change a data
// point or add a new one. If the data point index (i) is greater than the
// current size of the internal arrays, they are automatically extended.
//
// Specific drawing options can be used to paint a TGraph2D:
// "TRI" : The Delaunay triangles are drawn using filled area.
// An hidden surface drawing technique is used. The surface is
// painted with the current fill area color. The edges of each
// triangles are painted with the current line color.
// "TRIW" : The Delaunay triangles are drawn as wire frame
// "TRI1" : The Delaunay triangles are painted with color levels. The edges
// of each triangles are painted with the current line color.
// "TRI2" : the Delaunay triangles are painted with color levels.
// "P" : Draw a marker at each vertex
// "P0" : Draw a circle at each vertex. Each circle background is white.
//
// A TGraph2D can be also drawn with ANY options valid to draw a 2D histogram.
//
// When a TGraph2D is drawn with one of the 2D histogram drawing option,
// a intermediate 2D histogram is filled using the Delaunay triangles
// technique to interpolate the data set.
//
// TGraph2D linearly interpolate a Z value for any (X,Y) point given some
// existing (X,Y,Z) points. The existing (X,Y,Z) points can be randomly
// scattered. The algorithm works by joining the existing points to make
// Delaunay triangles in (X,Y). These are then used to define flat planes
// in (X,Y,Z) over which to interpolate. The interpolated surface thus takes
// the form of tessellating triangles at various angles. Output can take the
// form of a 2D histogram or a vector. The triangles found can be drawn in 3D.
//
// This software cannot be guaranteed to work under all circumstances. They
// were originally written to work with a few hundred points in an XY space
// with similar X and Y ranges.
//
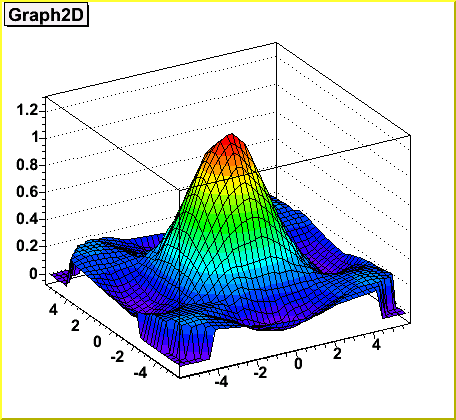
// The picture below has been generated by the following macro:
//
//{
// TCanvas *c = new TCanvas("c","Graph2D example",0,0,700,600);
// Double_t x, y, z, P = 6.;
// Int_t np = 200;
// TGraph2D *dt = new TGraph2D();
// TRandom *r = new TRandom();
// for (Int_t N=0; N<np; N++) {
// x = 2*P*(r->Rndm(N))-P;
// y = 2*P*(r->Rndm(N))-P;
// z = (sin(x)/x)*(sin(y)/y)+0.2;
// dt->SetPoint(N,x,y,z);
// }
// gStyle->SetPalette(1);
// dt->Draw("surf1");
//}
//
/*
*/
//
//
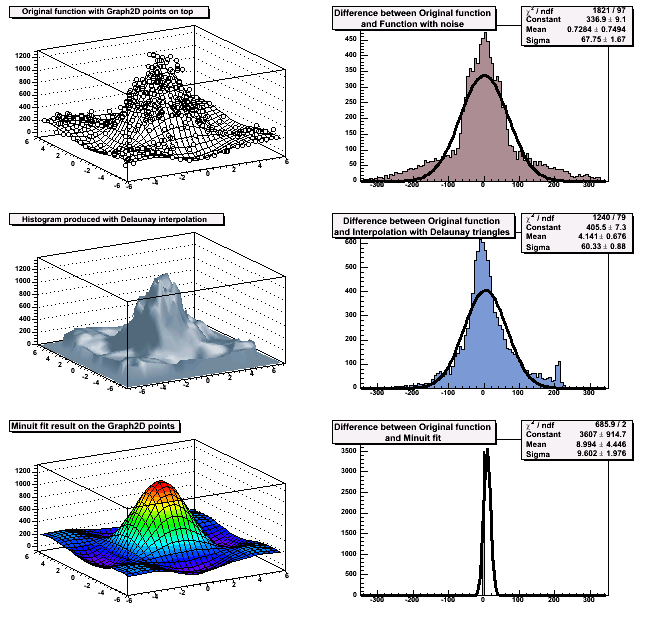
// A more complete example can be find in $ROOTSYS/tutorial/graph2dfit.C. It
// produces the following output:
//
//
/*
*/
//
//
// Definition of Delaunay triangulation (After B. Delaunay):
// For a set S of points in the Euclidean plane, the unique triangulation DT(S)
// of S such that no point in S is inside the circumcircle of any triangle in
// DT(S). DT(S) is the dual of the Voronoi diagram of S.
// If n is the number of points in S, the Voronoi diagram of S is the partitioning
// of the plane containing S points into n convex polygons such that each polygon
// contains exactly one point and every point in a given polygon is closer to its
// central point than to any other. A Voronoi diagram is sometimes also known as
// a Dirichlet tessellation.
//
/*
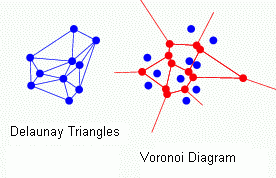
This applet
gives a nice practical view of Delaunay triangulation and Voronoi diagram.
*/
//
//______________________________________________________________________________
TGraph2D::TGraph2D()
: TNamed("Graph2D","Graph2D"), TAttLine(1,1,1), TAttFill(0,1001),
TAttMarker(), fNpoints(0)
{
// Graph2D default constructor
fSize = 0;
fMargin = 0.;
fNpx = 40;
fNpy = 40;
fDirectory = 0;
fHistogram = 0;
fMaximum = -1111;
fMinimum = -1111;
fX = 0;
fY = 0;
fZ = 0;
fZout = 0;
fMaxIter = 100000;
fPainter = 0;
fFunctions = new TList;
fUserHisto = kFALSE;
}
//______________________________________________________________________________
TGraph2D::TGraph2D(Int_t n, Int_t *x, Int_t *y, Int_t *z)
: TNamed("Graph2D","Graph2D"), TAttLine(1,1,1), TAttFill(0,1001),
TAttMarker(), fNpoints(n)
{
// Graph2D constructor with three vectors of ints as input.
Build(n);
// Copy the input vectors into local arrays
for (Int_t n=0; n<fNpoints; n++) {
fX[n] = (Double_t)x[n];
fY[n] = (Double_t)y[n];
fZ[n] = (Double_t)z[n];
}
}
//______________________________________________________________________________
TGraph2D::TGraph2D(Int_t n, Float_t *x, Float_t *y, Float_t *z)
: TNamed("Graph2D","Graph2D"), TAttLine(1,1,1), TAttFill(0,1001),
TAttMarker(), fNpoints(n)
{
// Graph2D constructor with three vectors of floats as input.
Build(n);
// Copy the input vectors into local arrays
for (Int_t n=0; n<fNpoints; n++) {
fX[n] = x[n];
fY[n] = y[n];
fZ[n] = z[n];
}
}
//______________________________________________________________________________
TGraph2D::TGraph2D(Int_t n, Double_t *x, Double_t *y, Double_t *z)
: TNamed("Graph2D","Graph2D"), TAttLine(1,1,1), TAttFill(0,1001),
TAttMarker(), fNpoints(n)
{
// Graph2D constructor with three vectors of doubles as input.
Build(n);
// Copy the input vectors into local arrays
for (Int_t n=0; n<fNpoints; n++) {
fX[n] = x[n];
fY[n] = y[n];
fZ[n] = z[n];
}
}
//______________________________________________________________________________
TGraph2D::TGraph2D(TH2 *h2)
: TNamed("Graph2D","Graph2D"), TAttLine(1,1,1), TAttFill(0,1001),
TAttMarker(), fNpoints(0)
{
// Graph2D constructor with a TH2 (h2) as input.
// Only the h2's bins within the X and Y axis ranges are used.
Build(10);
SetName(h2->GetName());
SetTitle(h2->GetTitle());
TAxis *xaxis = h2->GetXaxis();
TAxis *yaxis = h2->GetYaxis();
Int_t xfirst = xaxis->GetFirst();
Int_t xlast = xaxis->GetLast();
Int_t yfirst = yaxis->GetFirst();
Int_t ylast = yaxis->GetLast();
Double_t hmin = h2->GetMinimum();
Double_t hmax = h2->GetMaximum();
Double_t x, y, z;
Int_t k=0;
for (Int_t i=xfirst; i<= xlast; i++) {
for (Int_t j=yfirst; j<= ylast; j++) {
x = xaxis->GetBinCenter(i);
y = yaxis->GetBinCenter(j);
z = h2->GetBinContent(i,j);
if (z>hmin && z<hmax) {
SetPoint(k, x, y, z);
k++;
}
}
}
}
//______________________________________________________________________________
TGraph2D::TGraph2D(const char *name,const char *title,
Int_t n, Double_t *x, Double_t *y, Double_t *z)
: TNamed(name,title), TAttLine(1,1,1), TAttFill(0,1001),
TAttMarker(), fNpoints(n)
{
// Graph2D constructor with name, title and three vectors of doubles as input.
// name : name of 2D graph (avoid blanks)
// title : 2D graph title
// if title is of the form "stringt;stringx;stringy;stringz"
// the 2D graph title is set to stringt, the x axis title to stringy,
// the y axis title to stringy,etc
Build(n);
// Copy the input vectors into local arrays
for (Int_t n=0; n<fNpoints; n++) {
fX[n] = x[n];
fY[n] = y[n];
fZ[n] = z[n];
}
}
//______________________________________________________________________________
TGraph2D::TGraph2D(Int_t n)
: TNamed("Graph2D","Graph2D"), TAttLine(1,1,1), TAttFill(0,1001),
TAttMarker(), fNpoints(0)
{
// Graph2D constructor. The arrays fX, fY and fZ should be filled via
// calls to SetPoint
Build(n);
}
//______________________________________________________________________________
TGraph2D::TGraph2D(const char *filename, const char *format, Option_t *)
: TNamed("Graph2D",filename), TAttLine(1,1,1), TAttFill(0,1001),
TAttMarker(), fNpoints(0)
{
// Graph2D constructor reading input from filename
// filename is assumed to contain at least three columns of numbers
Build(100);
Double_t x,y,z;
FILE *fp = fopen(filename,"r");
if (!fp) {
MakeZombie();
Error("TGraph2D", "Cannot open file: %s, TGraph2D is Zombie",filename);
return;
}
char line[80];
Int_t np = 0;
while (fgets(line,80,fp)) {
sscanf(&line[0],format,&x, &y, &z);
SetPoint(np,x,y,z);
np++;
}
fclose(fp);
}
//______________________________________________________________________________
TGraph2D::TGraph2D(const TGraph2D &g)
: TNamed(g), TAttLine(g), TAttFill(g), TAttMarker(g)
{
// Graph2D copy constructor.
fNpoints = g.fNpoints;
Build(fNpoints);
for (Int_t n=0; n<fNpoints; n++) {
fX[n] = g.fX[n];
fY[n] = g.fY[n];
fZ[n] = g.fZ[n];
}
}
//______________________________________________________________________________
TGraph2D::~TGraph2D()
{
// TGraph2D destructor.
if (fX) delete [] fX;
if (fY) delete [] fY;
if (fZ) delete [] fZ;
if (fHistogram) delete fHistogram;
if (fFunctions) {
fFunctions->SetBit(kInvalidObject);
fFunctions->Delete();
delete fFunctions;
}
if (fDirectory) {
if (!fDirectory->TestBit(TDirectory::kCloseDirectory))
fDirectory->GetList()->Remove(this);
}
if (fPainter) delete fPainter;
fX = 0;
fY = 0;
fZ = 0;
fHistogram = 0;
fDirectory = 0;
fFunctions = 0;
}
//______________________________________________________________________________
TGraph2D TGraph2D::operator=(const TGraph2D &g)
{
// Graph2D operator "="
if (this == &g) return *this;
fNpoints = g.fNpoints;
Build(fNpoints);
for (Int_t n=0; n<fNpoints; n++) {
fX[n] = g.fX[n];
fY[n] = g.fY[n];
fZ[n] = g.fZ[n];
}
return g;
}
//______________________________________________________________________________
void TGraph2D::Build(Int_t n)
{
// Creates the 2D graph basic data structure
if (n <= 0) {
Error("TGraph2D", "Invalid number of points (%d)", n);
return;
}
fSize = n;
fMargin = 0.;
fNpx = 40;
fNpy = 40;
fDirectory = 0;
fHistogram = 0;
fMaximum = -1111;
fMinimum = -1111;
fX = new Double_t[fSize];
fY = new Double_t[fSize];
fZ = new Double_t[fSize];
fZout = 0;
fMaxIter = 100000;
fFunctions = new TList;
fPainter = 0;
fUserHisto = kFALSE;
Bool_t add = TH1::AddDirectoryStatus();
if (add && gDirectory) {
TObject *old = (TObject*)gDirectory->GetList()->FindObject(GetName());
if (old) {
Warning("Build","Replacing existing 2D graph: %s (Potential memory leak).",GetName());
gDirectory->GetList()->Remove(old);
}
gDirectory->Append(this);
fDirectory = gDirectory;
}
}
//______________________________________________________________________________
Int_t TGraph2D::DistancetoPrimitive(Int_t px, Int_t py)
{
// Computes distance from point px,py to a graph
Int_t distance = 9999;
if (fHistogram) distance = fHistogram->DistancetoPrimitive(px,py);
return distance;
}
//______________________________________________________________________________
void TGraph2D::Draw(Option_t *option)
{
// Specific drawing options can be used to paint a TGraph2D:
// "TRI" : The Delaunay triangles are drawn using filled area.
// An hidden surface drawing technique is used. The surface is
// painted with the current fill area color. The edges of each
// triangles are painted with the current line color.
// "TRIW" : The Delaunay triangles are drawn as wire frame
// "TRI1" : The Delaunay triangles are painted with color levels. The edges
// of each triangles are painted with the current line color.
// "TRI2" : the Delaunay triangles are painted with color levels.
// "P" : Draw a marker at each vertex
// "P0" : Draw a circle at each vertex. Each circle background is white.
//
// A TGraph2D can be also drawn with ANY options valid to draw a 2D histogram.
//
// When a TGraph2D is drawn with one of the 2D histogram drawing option,
// a intermediate 2D histogram is filled using the Delaunay triangles
// technique to interpolate the data set.
TString opt = option;
opt.ToLower();
if (gPad) {
if (!gPad->IsEditable()) (gROOT->GetMakeDefCanvas())();
if (!opt.Contains("same")) {
//the following statement is necessary in case one attempts to draw
//a temporary histogram already in the current pad
if (TestBit(kCanDelete)) gPad->GetListOfPrimitives()->Remove(this);
gPad->Clear();
}
}
AppendPad(opt.Data());
}
//______________________________________________________________________________
void TGraph2D::ExecuteEvent(Int_t event, Int_t px, Int_t py)
{
// Executes action corresponding to one event
if (fHistogram) fHistogram->ExecuteEvent(event, px, py);
}
//______________________________________________________________________________
TObject *TGraph2D::FindObject(const char *name) const
{
// search object named name in the list of functions
if (fFunctions) return fFunctions->FindObject(name);
return 0;
}
//______________________________________________________________________________
TObject *TGraph2D::FindObject(const TObject *obj) const
{
// search object obj in the list of functions
if (fFunctions) return fFunctions->FindObject(obj);
return 0;
}
//______________________________________________________________________________
Int_t TGraph2D::Fit(const char *fname, Option_t *option, Option_t *)
{
// Fits this graph with function with name fname
// Predefined functions such as gaus, expo and poln are automatically
// created by ROOT.
// fname can also be a formula, accepted by the linear fitter (linear parts divided
// by "++" sign), for example "x++sin(x)" for fitting "[0]*x+[1]*sin(x)"
char *linear;
linear= (char*)strstr(fname, "++");
TF2 *f2=0;
if (linear)
f2=new TF2(fname, fname);
else{
f2 = (TF2*)gROOT->GetFunction(fname);
if (!f2) { Printf("Unknown function: %s",fname); return -1; }
}
return Fit(f2,option,"");
}
//______________________________________________________________________________
Int_t TGraph2D::Fit(TF2 *f2, Option_t *option, Option_t *)
{
// Fits this 2D graph with function f2
//
// f2 is an already predefined function created by TF2.
// Predefined functions such as gaus, expo and poln are automatically
// created by ROOT.
//
// The list of fit options is given in parameter option.
// option = "W" Set all errors to 1
// = "U" Use a User specified fitting algorithm (via SetFCN)
// = "Q" Quiet mode (minimum printing)
// = "V" Verbose mode (default is between Q and V)
// = "R" Use the Range specified in the function range
// = "N" Do not store the graphics function, do not draw
// = "0" Do not plot the result of the fit. By default the fitted function
// is drawn unless the option"N" above is specified.
// = "+" Add this new fitted function to the list of fitted functions
// (by default, any previous function is deleted)
// = "C" In case of linear fitting, not calculate the chisquare
// (saves time)
// = "ROB" In case of linear fitting, compute the LTS regression
// coefficients (robust(resistant) regression), using
// the default fraction of good points
// "ROB=0.x" - compute the LTS regression coefficients, using
// 0.x as a fraction of good points
//
// In order to use the Range option, one must first create a function
// with the expression to be fitted. For example, if your graph2d
// has a defined range between -4 and 4 and you want to fit a gaussian
// only in the interval 1 to 3, you can do:
// TF2 *f2 = new TF2("f2","gaus",1,3);
// graph2d->Fit("f2","R");
//
//
// Setting initial conditions
// ==========================
// Parameters must be initialized before invoking the Fit function.
// The setting of the parameter initial values is automatic for the
// predefined functions : poln, expo, gaus. One can however disable
// this automatic computation by specifying the option "B".
// You can specify boundary limits for some or all parameters via
// f2->SetParLimits(p_number, parmin, parmax);
// if parmin>=parmax, the parameter is fixed
// Note that you are not forced to fix the limits for all parameters.
// For example, if you fit a function with 6 parameters, you can do:
// func->SetParameters(0,3.1,1.e-6,0.1,-8,100);
// func->SetParLimits(4,-10,-4);
// func->SetParLimits(5, 1,1);
// With this setup, parameters 0->3 can vary freely
// Parameter 4 has boundaries [-10,-4] with initial value -8
// Parameter 5 is fixed to 100.
//
// Fit range
// =========
// The fit range can be specified in two ways:
// - specify rxmax > rxmin (default is rxmin=rxmax=0)
// - specify the option "R". In this case, the function will be taken
// instead of the full graph range.
//
// Changing the fitting function
// =============================
// By default the fitting function Graph2DFitChisquare is used.
// To specify a User defined fitting function, specify option "U" and
// call the following functions:
// TVirtualFitter::Fitter(mygraph)->SetFCN(MyFittingFunction)
// where MyFittingFunction is of type:
// extern void MyFittingFunction(Int_t &npar, Double_t *gin, Double_t &f, Double_t *u, Int_t flag);
//
// Associated functions
// ====================
// One or more object (typically a TF2*) can be added to the list
// of functions (fFunctions) associated to each graph.
// When TGraph::Fit is invoked, the fitted function is added to this list.
// Given a graph gr, one can retrieve an associated function
// with: TF2 *myfunc = gr->GetFunction("myfunc");
//
// Access to the fit results
// =========================
// If the graph is made persistent, the list of
// associated functions is also persistent. Given a pointer (see above)
// to an associated function myfunc, one can retrieve the function/fit
// parameters with calls such as:
// Double_t chi2 = myfunc->GetChisquare();
// Double_t par0 = myfunc->GetParameter(0); //value of 1st parameter
// Double_t err0 = myfunc->GetParError(0); //error on first parameter
//
// Fit Statistics
// ==============
// You can change the statistics box to display the fit parameters with
// the TStyle::SetOptFit(mode) method. This mode has four digits.
// mode = pcev (default = 0111)
// v = 1; print name/values of parameters
// e = 1; print errors (if e=1, v must be 1)
// c = 1; print Chisquare/Number of degress of freedom
// p = 1; print Probability
//
// For example: gStyle->SetOptFit(1011);
// prints the fit probability, parameter names/values, and errors.
// You can change the position of the statistics box with these lines
// (where g is a pointer to the TGraph):
//
// Root > TPaveStats *st = (TPaveStats*)g->GetListOfFunctions()->FindObject("stats")
// Root > st->SetX1NDC(newx1); //new x start position
// Root > st->SetX2NDC(newx2); //new x end position
Int_t fitResult = 0;
Double_t xmin=0, xmax=0;
Int_t i, npar,nvpar,nparx;
Double_t par, we, al, bl;
Double_t eplus,eminus,eparab,globcc,amin,edm,errdef,werr;
TF2 *fnew2;
// Check validity of function
if (!f2) {
Error("Fit", "function may not be null pointer");
return 0;
}
if (f2->IsZombie()) {
Error("Fit", "function is zombie");
return 0;
}
npar = f2->GetNpar();
if (npar <= 0) {
Error("Fit", "function %s has illegal number of parameters = %d", f2->GetName(), npar);
return 0;
}
// Check that function has same dimension as graph
if (f2->GetNdim() != 2) {
Error("Fit","function %s is not 2-D", f2->GetName());
return 0;
}
//}
Double_t *arglist = new Double_t[100];
// Decode string choptin and fill fitOption structure
Foption_t fitOption;
TString opt = option;
opt.ToUpper();
Double_t h=0;
opt.ReplaceAll("ROB", "H");
//for robust fitting, see if # of good points is defined
if (opt.Contains("H=0.")) {
int start = opt.Index("H=0.");
int numpos = start + strlen("H=0.");
int numlen = 0;
int len = opt.Length();
while( (numpos+numlen<len) && isdigit(opt[numpos+numlen]) ) numlen++;
TString num = opt(numpos,numlen);
opt.Remove(start+strlen("H"),strlen("=0.")+numlen);
h = atof(num.Data());
h*=TMath::Power(10, -numlen);
}
if (opt.Contains("U")) fitOption.User = 1;
if (opt.Contains("Q")) fitOption.Quiet = 1;
if (opt.Contains("V")){fitOption.Verbose = 1; fitOption.Quiet = 0;}
if (opt.Contains("W")) fitOption.W1 = 1;
if (opt.Contains("E")) fitOption.Errors = 1;
if (opt.Contains("R")) fitOption.Range = 1;
if (opt.Contains("N")) fitOption.Nostore = 1;
if (opt.Contains("0")) fitOption.Nograph = 1;
if (opt.Contains("+")) fitOption.Plus = 1;
if (opt.Contains("B")) fitOption.Bound = 1;
if (opt.Contains("C")) fitOption.Nochisq = 1;
if (opt.Contains("H")) fitOption.Robust = 1;
///xmin = fX[0];
///xmax = fX[fNpoints-1];
///ymin = fY[0];
///ymax = fY[fNpoints-1];
///Double_t err0 = GetErrorX(0);
///Double_t errn = GetErrorX(fNpoints-1);
///if (err0 > 0) xmin -= 2*err0;
///if (errn > 0) xmax += 2*errn;
///for (i=0;i<fNpoints;i++) {
/// if (fX[i] < xmin) xmin = fX[i];
/// if (fX[i] > xmax) xmax = fX[i];
/// if (fY[i] < ymin) ymin = fY[i];
/// if (fY[i] > ymax) ymax = fY[i];
///}
///if (rxmax > rxmin) {
/// xmin = rxmin;
/// xmax = rxmax;
///}
// Check if Minuit is initialized and create special functions
Bool_t linear = f2->IsLinear();
if (fitOption.Bound || fitOption.User || fitOption.Errors)
linear = kFALSE;
char l[]="TLinearFitter";
Int_t strdiff = 0;
Bool_t isSet = kFALSE;
if (TVirtualFitter::GetFitter()){
//Is a fitter already set? Is it linear?
isSet=kTRUE;
strdiff = strcmp(TVirtualFitter::GetFitter()->IsA()->GetName(), l);
}
if (linear){
//
TClass *cl = gROOT->GetClass("TLinearFitter");
if (isSet && strdiff!=0) {
delete TVirtualFitter::GetFitter();
isSet=kFALSE;
}
if (!isSet) {
//TLinearFitter *lf=(TLinearFitter *)cl->New();
TVirtualFitter::SetFitter((TVirtualFitter *)cl->New());
}
} else {
if (isSet && strdiff==0){
delete TVirtualFitter::GetFitter();
isSet=kFALSE;
}
if (!isSet)
TVirtualFitter::SetFitter(0);
}
TVirtualFitter *grFitter = TVirtualFitter::Fitter(this, f2->GetNpar());
grFitter->Clear();
// Get pointer to the function by searching in the list of functions in ROOT
grFitter->SetUserFunc(f2);
grFitter->SetFitOption(fitOption);
//*-*- Is a Fit range specified?
Int_t gxfirst, gxlast;
///if (fitOption.Range) {
/// f2->GetRange(xmin, ymin, xmax, ymax);
/// gxfirst = fNpoints +1;
/// gxlast = -1;
/// for (i=0;i<fNpoints;i++) {
/// if (fX[i] >= xmin && gxfirst > i) gxfirst = i;
/// if (fX[i] <= xmax && gxlast < i) gxlast = i;
/// }
///} else {
/// f2->SetRange(xmin, ymin, xmax, ymax);
gxfirst = 0;
gxlast = fNpoints-1;
///}
if (linear){
if (fitOption.Robust)
grFitter->ExecuteCommand("FitGraph2D", &h, 0);
else
grFitter->ExecuteCommand("FitGraph2D", 0, 0);
} else {
// Some initialisations
if (!fitOption.Verbose) {
arglist[0] = -1;
grFitter->ExecuteCommand("SET PRINT", arglist,1);
arglist[0] = 0;
grFitter->ExecuteCommand("SET NOW", arglist,0);
}
// Set error criterion for chisquare
arglist[0] = 1;
if (!fitOption.User) grFitter->SetFitMethod("Graph2DFitChisquare");
fitResult = grFitter->ExecuteCommand("SET ERR",arglist,1);
if (fitResult != 0) {
// Abnormal termination, MIGRAD might not have converged on a minimum.
if (!fitOption.Quiet) {
Warning("Fit","Abnormal termination of minimization.");
}
delete [] arglist;
return fitResult;
}
// Transfer names and initial values of parameters to Minuit
Int_t nfixed = 0;
for (i=0;i<npar;i++) {
par = f2->GetParameter(i);
f2->GetParLimits(i,al,bl);
if (al*bl != 0 && al >= bl) {
al = bl = 0;
arglist[nfixed] = i+1;
nfixed++;
}
we = 0.3*TMath::Abs(par);
if (we <= TMath::Abs(par)*1e-6) we = 1;
grFitter->SetParameter(i,f2->GetParName(i),par,we,al,bl);
}
if(nfixed > 0)grFitter->ExecuteCommand("FIX",arglist,nfixed); // Otto
// Reset Print level
if (fitOption.Verbose) {
arglist[0] = 0; grFitter->ExecuteCommand("SET PRINT", arglist,1);
}
// Compute sum of squares of errors in the bin range
Bool_t hasErrors = kFALSE;
Double_t ex, ey, ez, sumw2=0;
for (i=gxfirst;i<=gxlast;i++) {
ex = GetErrorX(i);
ey = GetErrorY(i);
ez = GetErrorZ(i);
if (ex > 0 || ey > 0 || ez > 0) hasErrors = kTRUE;
sumw2 += ez*ez;
}
//*-*- Perform minimization
arglist[0] = TVirtualFitter::GetMaxIterations();
arglist[1] = sumw2*TVirtualFitter::GetPrecision();
grFitter->ExecuteCommand("MIGRAD",arglist,2);
if (fitOption.Errors) {
grFitter->ExecuteCommand("HESSE",arglist,0);
grFitter->ExecuteCommand("MINOS",arglist,0);
}
grFitter->GetStats(amin,edm,errdef,nvpar,nparx);
f2->SetChisquare(amin);
Int_t ndf = f2->GetNumberFitPoints()-npar+nfixed;
f2->SetNDF(ndf);
// Get return status
char parName[50];
for (i=0;i<npar;i++) {
grFitter->GetParameter(i,parName, par,we,al,bl);
if (!fitOption.Errors) werr = we;
else {
grFitter->GetErrors(i,eplus,eminus,eparab,globcc);
if (eplus > 0 && eminus < 0) werr = 0.5*(eplus-eminus);
else werr = we;
}
if (!hasErrors && ndf > 1) werr *= TMath::Sqrt(amin/(ndf-1));
f2->SetParameter(i,par);
f2->SetParError(i,werr);
}
}
// Print final values of parameters.
if (!fitOption.Quiet) {
if (fitOption.Errors) grFitter->PrintResults(4,amin);
else grFitter->PrintResults(3,amin);
}
delete [] arglist;
// Store fitted function in histogram functions list and draw
if (!fitOption.Nostore) {
if (!fFunctions) fFunctions = new TList;
if (!fitOption.Plus) {
TIter next(fFunctions, kIterBackward);
TObject *obj;
while ((obj = next())) {
if (obj->InheritsFrom(TF1::Class())) delete obj;
}
}
fnew2 = new TF2();
f2->Copy(*fnew2);
fFunctions->Add(fnew2);
fnew2->SetParent(this);
fnew2->Save(xmin,xmax,0,0,0,0);
if (fitOption.Nograph) fnew2->SetBit(TF1::kNotDraw);
fnew2->SetBit(TFormula::kNotGlobal);
if (TestBit(kCanDelete)) return fitResult;
if (gPad) gPad->Modified();
}
return fitResult;
}
//______________________________________________________________________________
TAxis *TGraph2D::GetXaxis() const
{
// Get x axis of the graph.
//if (!gPad) return 0;
TH1 *h = ((TGraph2D*)this)->GetHistogram();
if (!h) return 0;
return h->GetXaxis();
}
//______________________________________________________________________________
TAxis *TGraph2D::GetYaxis() const
{
// Get y axis of the graph.
//if (!gPad) return 0;
TH1 *h = ((TGraph2D*)this)->GetHistogram();
if (!h) return 0;
return h->GetYaxis();
}
//______________________________________________________________________________
TAxis *TGraph2D::GetZaxis() const
{
// Get z axis of the graph.
//if (!gPad) return 0;
TH1 *h = ((TGraph2D*)this)->GetHistogram();
if (!h) return 0;
return h->GetZaxis();
}
//______________________________________________________________________________
TList *TGraph2D::GetContourList(Double_t contour)
{
// Returns the X and Y graphs building a contour. A contour level may
// consist in several parts not connected to each other. This function
// returns them in a graphs' list.
if (fNpoints <= 0) {
Error("GetContourList", "Empty TGraph2D");
return 0;
}
if(!fHistogram) GetHistogram("empty");
if (!fPainter) fPainter = fHistogram->GetPainter();
return fPainter->GetContourList(contour);
}
//______________________________________________________________________________
Double_t TGraph2D::GetErrorX(Int_t) const
{
// This function is called by Graph2DFitChisquare.
// It always returns a negative value. Real implementation in TGraph2DErrors
return -1;
}
//______________________________________________________________________________
Double_t TGraph2D::GetErrorY(Int_t) const
{
// This function is called by Graph2DFitChisquare.
// It always returns a negative value. Real implementation in TGraph2DErrors
return -1;
}
//______________________________________________________________________________
Double_t TGraph2D::GetErrorZ(Int_t) const
{
// This function is called by Graph2DFitChisquare.
// It always returns a negative value. Real implementation in TGraph2DErrors
return -1;
}
//______________________________________________________________________________
TH2D *TGraph2D::GetHistogram(Option_t *option)
{
// By default returns a pointer to the Delaunay histogram. If fHistogram
// doesn't exist, books the 2D histogram fHistogram with a margin around
// the hull. Calls TGraphDelaunay::Interpolate at each bin centre to build up
// an interpolated 2D histogram.
// If the "empty" option is selected, returns an empty histogram booked with
// the limits of fX, fY and fZ. This option is used when the data set is
// drawn with markers only. In that particular case there is no need to
// find the Delaunay triangles.
if (fNpoints <= 0) {
Error("GetHistogram", "Empty TGraph2D");
return 0;
}
TString opt = option;
opt.ToLower();
Bool_t empty = opt.Contains("empty");
if (fHistogram) {
if (!empty && fHistogram->GetEntries()==0) {
if (!fUserHisto) {
delete fHistogram;
fHistogram = 0;
}
} else {
return fHistogram;
}
}
Double_t hxmax, hymax, hxmin, hymin;
// Book fHistogram if needed. It is not added in the current directory
if (!fUserHisto) {
Bool_t add = TH1::AddDirectoryStatus();
TH1::AddDirectory(kFALSE);
Double_t xmax = GetXmax();
Double_t ymax = GetYmax();
Double_t xmin = GetXmin();
Double_t ymin = GetYmin();
hxmin = xmin-fMargin*(xmax-xmin);
hymin = ymin-fMargin*(ymax-ymin);
hxmax = xmax+fMargin*(xmax-xmin);
hymax = ymax+fMargin*(ymax-ymin);
fHistogram = new TH2D(GetName(),GetTitle(),
fNpx ,hxmin, hxmax,
fNpy, hymin, hymax);
TH1::AddDirectory(add);
fHistogram->SetBit(TH1::kNoStats);
} else {
hxmin = fHistogram->GetXaxis()->GetXmin();
hymin = fHistogram->GetYaxis()->GetXmin();
hxmax = fHistogram->GetXaxis()->GetXmax();
hymax = fHistogram->GetYaxis()->GetXmax();
}
// Add a TGraphDelaunay in the list of the fHistogram's functions
TGraphDelaunay *dt = new TGraphDelaunay(this);
dt->SetMaxIter(fMaxIter);
dt->SetMarginBinsContent(fZout);
TList *hl = fHistogram->GetListOfFunctions();
hl->Add(dt);
// Option "empty" is selected. An empty histogram is returned.
if (empty) {
if (fMinimum != -1111) {
fHistogram->SetMinimum(fMinimum);
} else {
fHistogram->SetMinimum(GetZmin());
}
if (fMaximum != -1111) {
fHistogram->SetMaximum(fMaximum);
} else {
fHistogram->SetMaximum(GetZmax());
}
return fHistogram;
}
Double_t dx = (hxmax-hxmin)/fNpx;
Double_t dy = (hymax-hymin)/fNpy;
Double_t x, y, z;
for (Int_t ix=1; ix<=fNpx; ix++) {
x = hxmin+(ix-0.5)*dx;
for (Int_t iy=1; iy<=fNpy; iy++) {
y = hymin+(iy-0.5)*dy;
z = dt->ComputeZ(x, y);
fHistogram->Fill(x, y, z);
}
}
if (fMinimum != -1111) fHistogram->SetMinimum(fMinimum);
if (fMaximum != -1111) fHistogram->SetMaximum(fMaximum);
return fHistogram;
}
//______________________________________________________________________________
Double_t TGraph2D::GetXmax() const
{
// Returns the X maximum
Double_t v = fX[0];
for (Int_t i=1; i<fNpoints; i++) if (fX[i]>v) v=fX[i];
return v;
}
//______________________________________________________________________________
Double_t TGraph2D::GetXmin() const
{
// Returns the X minimum
Double_t v = fX[0];
for (Int_t i=1; i<fNpoints; i++) if (fX[i]<v) v=fX[i];
return v;
}
//______________________________________________________________________________
Double_t TGraph2D::GetYmax() const
{
// Returns the Y maximum
Double_t v = fY[0];
for (Int_t i=1; i<fNpoints; i++) if (fY[i]>v) v=fY[i];
return v;
}
//______________________________________________________________________________
Double_t TGraph2D::GetYmin() const
{
// Returns the Y minimum
Double_t v = fY[0];
for (Int_t i=1; i<fNpoints; i++) if (fY[i]<v) v=fY[i];
return v;
}
//______________________________________________________________________________
Double_t TGraph2D::GetZmax() const
{
// Returns the Z maximum
Double_t v = fZ[0];
for (Int_t i=1; i<fNpoints; i++) if (fZ[i]>v) v=fZ[i];
return v;
}
//______________________________________________________________________________
Double_t TGraph2D::GetZmin() const
{
// Returns the Z minimum
Double_t v = fZ[0];
for (Int_t i=1; i<fNpoints; i++) if (fZ[i]<v) v=fZ[i];
return v;
}
//______________________________________________________________________________
Double_t TGraph2D::Interpolate(Double_t x, Double_t y)
{
// Finds the z value at the position (x,y) thanks to
// the Delaunay interpolation.
if (fNpoints <= 0) {
Error("Interpolate", "Empty TGraph2D");
return 0;
}
TGraphDelaunay *dt;
if(!fHistogram) GetHistogram("empty");
TList *hl = fHistogram->GetListOfFunctions();
dt = (TGraphDelaunay*)hl->FindObject("TGraphDelaunay");
return dt->ComputeZ(x, y);
}
//______________________________________________________________________________
void TGraph2D::Paint(Option_t *option)
{
// Paints this 2D graph with its current attributes
if (fNpoints <= 0) {
Error("Paint", "Empty TGraph2D");
return;
}
TString opt = option;
opt.ToLower();
if (opt.Contains("p") && !opt.Contains("tri")) {
if (!opt.Contains("pol") &&
!opt.Contains("sph") &&
!opt.Contains("psr")) opt.Append("tri0");
}
if (opt.Contains("line") && !opt.Contains("tri")) opt.Append("tri0");
if (opt.Contains("tri0")) {
GetHistogram("empty");
} else {
GetHistogram();
}
fHistogram->SetLineColor(GetLineColor());
fHistogram->SetLineStyle(GetLineStyle());
fHistogram->SetLineWidth(GetLineWidth());
fHistogram->SetFillColor(GetFillColor());
fHistogram->SetFillStyle(GetFillStyle());
fHistogram->SetMarkerColor(GetMarkerColor());
fHistogram->SetMarkerStyle(GetMarkerStyle());
fHistogram->SetMarkerSize(GetMarkerSize());
fHistogram->Paint(opt.Data());
}
//______________________________________________________________________________
TH1 *TGraph2D::Project(Option_t *option) const
{
// Projects a 2-d graph into 1 or 2-d histograms depending on the
// option parameter
// option may contain a combination of the characters x,y,z
// option = "x" return the x projection into a TH1D histogram
// option = "y" return the y projection into a TH1D histogram
// option = "xy" return the x versus y projection into a TH2D histogram
// option = "yx" return the y versus x projection into a TH2D histogram
if (fNpoints <= 0) {
Error("Project", "Empty TGraph2D");
return 0;
}
TString opt = option; opt.ToLower();
Int_t pcase = 0;
if (opt.Contains("x")) pcase = 1;
if (opt.Contains("y")) pcase = 2;
if (opt.Contains("xy")) pcase = 3;
if (opt.Contains("yx")) pcase = 4;
// Create the projection histogram
TH1D *h1 = 0;
TH2D *h2 = 0;
Int_t nch = strlen(GetName()) +opt.Length() +2;
char *name = new char[nch];
sprintf(name,"%s_%s",GetName(),option);
nch = strlen(GetTitle()) +opt.Length() +2;
char *title = new char[nch];
sprintf(title,"%s_%s",GetTitle(),option);
Double_t hxmin = GetXmin();
Double_t hxmax = GetXmax();
Double_t hymin = GetYmin();
Double_t hymax = GetYmax();
switch (pcase) {
case 1:
// "x"
h1 = new TH1D(name,title,fNpx,hxmin,hxmax);
break;
case 2:
// "y"
h1 = new TH1D(name,title,fNpy,hymin,hymax);
break;
case 3:
// "xy"
h2 = new TH2D(name,title,fNpx,hxmin,hxmax,fNpy,hymin,hymax);
break;
case 4:
// "yx"
h2 = new TH2D(name,title,fNpy,hymin,hymax,fNpx,hxmin,hxmax);
break;
}
delete [] name;
delete [] title;
TH1 *h = h1;
if (h2) h = h2;
if (h == 0) return 0;
// Fill the projected histogram
Double_t entries = 0;
for (Int_t n=0; n<fNpoints; n++) {
switch (pcase) {
case 1:
// "x"
h1->Fill(fX[n], fZ[n]);
break;
case 2:
// "y"
h1->Fill(fY[n], fZ[n]);
break;
case 3:
// "xy"
h2->Fill(fX[n], fY[n], fZ[n]);
break;
case 4:
// "yx"
h2->Fill(fY[n], fX[n], fZ[n]);
break;
}
entries += fZ[n];
}
h->SetEntries(entries);
return h;
}
//______________________________________________________________________________
Int_t TGraph2D::RemovePoint(Int_t ipoint)
{
// Deletes point number ipoint
if (ipoint < 0) return -1;
if (ipoint >= fNpoints) return -1;
fNpoints--;
Double_t *newX = new Double_t[fNpoints];
Double_t *newY = new Double_t[fNpoints];
Double_t *newZ = new Double_t[fNpoints];
Int_t j = -1;
for (Int_t i=0;i<fNpoints+1;i++) {
if (i == ipoint) continue;
j++;
newX[j] = fX[i];
newY[j] = fY[i];
newZ[j] = fZ[i];
}
delete [] fX;
delete [] fY;
delete [] fZ;
fX = newX;
fY = newY;
fZ = newZ;
if (fHistogram) {delete fHistogram; fHistogram = 0;}
return ipoint;
}
//______________________________________________________________________________
void TGraph2D::SavePrimitive(ofstream &out, Option_t *option)
{
// Saves primitive as a C++ statement(s) on output stream out
char quote = '"';
out<<" "<<endl;
if (gROOT->ClassSaved(TGraph2D::Class())) {
out<<" ";
} else {
out<<" TGraph2D *";
}
out<<"graph = new TGraph2D("<<fNpoints<<");"<<endl;
out<<" graph->SetName("<<quote<<GetName()<<quote<<");"<<endl;
out<<" graph->SetTitle("<<quote<<GetTitle()<<quote<<");"<<endl;
if (fDirectory == 0) {
out<<" "<<GetName()<<"->SetDirectory(0);"<<endl;
}
SaveFillAttributes(out,"graph",0,1001);
SaveLineAttributes(out,"graph",1,1,1);
SaveMarkerAttributes(out,"graph",1,1,1);
for (Int_t i=0;i<fNpoints;i++) {
out<<" graph->SetPoint("<<i<<","<<fX[i]<<","<<fY[i]<<","<<fZ[i]<<");"<<endl;
}
// save list of functions
TIter next(fFunctions);
TObject *obj;
while ((obj=next())) {
obj->SavePrimitive(out,"nodraw");
out<<" graph->GetListOfFunctions()->Add("<<obj->GetName()<<");"<<endl;
if (obj->InheritsFrom("TPaveStats")) {
out<<" ptstats->SetParent(graph->GetListOfFunctions());"<<endl;
}
}
out<<" graph->Draw("<<quote<<option<<quote<<");"<<endl;
}
//______________________________________________________________________________
void TGraph2D::SetDirectory(TDirectory *dir)
{
// By default when an 2D graph is created, it is added to the list
// of 2D graph objects in the current directory in memory.
// Remove reference to this 2D graph from current directory and add
// reference to new directory dir. dir can be 0 in which case the
// 2D graph does not belong to any directory.
if (fDirectory == dir) return;
if (fDirectory) fDirectory->GetList()->Remove(this);
fDirectory = dir;
if (fDirectory) fDirectory->GetList()->Add(this);
}
//______________________________________________________________________________
void TGraph2D::SetHistogram(TH2 *h)
{
// Sets the histogram to be filled
fUserHisto = kTRUE;
fHistogram = (TH2D*)h;
fNpx = h->GetNbinsX();
fNpy = h->GetNbinsY();
}
//______________________________________________________________________________
void TGraph2D::SetMargin(Double_t m)
{
// Sets the extra space (in %) around interpolated area for the 2D histogram
if (m<0 || m>1) {
Warning("SetMargin","The margin must be >= 0 && <= 1, fMargin set to 0.1");
fMargin = 0.1;
} else {
fMargin = m;
}
if (fHistogram) {delete fHistogram; fHistogram = 0;}
}
//______________________________________________________________________________
void TGraph2D::SetMarginBinsContent(Double_t z)
{
// Sets the histogram bin height for points lying outside the TGraphDelaunay
// convex hull ie: the bins in the margin.
fZout = z;
if (fHistogram) {delete fHistogram; fHistogram = 0;}
}
//______________________________________________________________________________
void TGraph2D::SetMaximum(Double_t maximum)
{
fMaximum = maximum;
GetHistogram()->SetMaximum(maximum);
}
//______________________________________________________________________________
void TGraph2D::SetMinimum(Double_t minimum)
{
fMinimum = minimum;
GetHistogram()->SetMinimum(minimum);
}
//______________________________________________________________________________
void TGraph2D::SetName(const char *name)
{
// Changes the name of this 2D graph
// 2D graphs are named objects in a THashList.
// We must update the hashlist if we change the name
if (fDirectory) fDirectory->GetList()->Remove(this);
fName = name;
if (fDirectory) fDirectory->GetList()->Add(this);
}
//______________________________________________________________________________
void TGraph2D::SetNpx(Int_t npx)
{
// Sets the number of bins along X used to draw the function
if (npx < 4) {
Warning("SetNpx","Number of points must be >4 && < 500, fNpx set to 4");
fNpx = 4;
} else if(npx > 500) {
Warning("SetNpx","Number of points must be >4 && < 500, fNpx set to 500");
fNpx = 500;
} else {
fNpx = npx;
}
if (fHistogram) {delete fHistogram; fHistogram = 0;}
}
//______________________________________________________________________________
void TGraph2D::SetNpy(Int_t npy)
{
// Sets the number of bins along Y used to draw the function
if (npy < 4) {
Warning("SetNpy","Number of points must be >4 && < 500, fNpy set to 4");
fNpy = 4;
} else if(npy > 500) {
Warning("SetNpy","Number of points must be >4 && < 500, fNpy set to 500");
fNpy = 500;
} else {
fNpy = npy;
}
if (fHistogram) {delete fHistogram; fHistogram = 0;}
}
//______________________________________________________________________________
void TGraph2D::SetPoint(Int_t n, Double_t x, Double_t y, Double_t z)
{
// Sets point number n.
// If n is greater than the current size, the arrays are automatically
// extended.
if (n < 0) return;
if (!fX || !fY || !fZ || n >= fSize) {
// re-allocate the object
Int_t newN = TMath::Max(2*fSize,n+1);
Double_t *savex = new Double_t [newN];
Double_t *savey = new Double_t [newN];
Double_t *savez = new Double_t [newN];
if (fX && fSize) {
memcpy(savex,fX,fSize*sizeof(Double_t));
memset(&savex[fSize],0,(newN-fSize)*sizeof(Double_t));
delete [] fX;
}
if (fY && fSize) {
memcpy(savey,fY,fSize*sizeof(Double_t));
memset(&savey[fSize],0,(newN-fSize)*sizeof(Double_t));
delete [] fY;
}
if (fZ && fSize) {
memcpy(savez,fZ,fSize*sizeof(Double_t));
memset(&savez[fSize],0,(newN-fSize)*sizeof(Double_t));
delete [] fZ;
}
fX = savex;
fY = savey;
fZ = savez;
fSize = newN;
}
fX[n] = x;
fY[n] = y;
fZ[n] = z;
fNpoints = TMath::Max(fNpoints,n+1);
}
//______________________________________________________________________________
void TGraph2D::SetTitle(const char* title)
{
// Sets graph title
fTitle = title;
if (fHistogram) fHistogram->SetTitle(title);
}
//_______________________________________________________________________
void TGraph2D::Streamer(TBuffer &b)
{
// Stream a class object
if (b.IsReading()) {
UInt_t R__s, R__c;
Version_t R__v = b.ReadVersion(&R__s, &R__c);
TGraph2D::Class()->ReadBuffer(b, this, R__v, R__s, R__c);
if (!gROOT->ReadingObject()) {
fDirectory = gDirectory;
if (!gDirectory->GetList()->FindObject(this)) gDirectory->Append(this);
}
ResetBit(kCanDelete);
} else {
TGraph2D::Class()->WriteBuffer(b,this);
}
}
ROOT page - Class index - Class Hierarchy - Top of the page
This page has been automatically generated. If you have any comments or suggestions about the page layout send a mail to ROOT support, or contact the developers with any questions or problems regarding ROOT.