// @(#)root/geom:$Name: $:$Id: TGeoCone.cxx,v 1.53 2005/09/04 15:12:08 brun Exp $
// Author: Andrei Gheata 31/01/02
// TGeoCone::Contains() and DistFromInside() implemented by Mihaela Gheata
/*************************************************************************
* Copyright (C) 1995-2000, Rene Brun and Fons Rademakers. *
* All rights reserved. *
* *
* For the licensing terms see $ROOTSYS/LICENSE. *
* For the list of contributors see $ROOTSYS/README/CREDITS. *
*************************************************************************/
//--------------------------------------------------------------------------
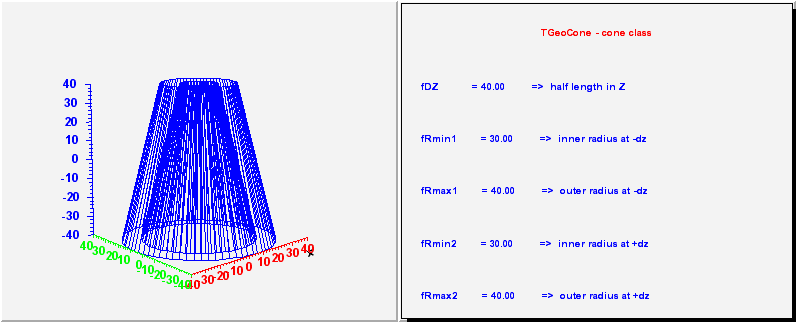
// TGeoCone - conical tube class. It has 5 parameters :
// dz - half length in z
// Rmin1, Rmax1 - inside and outside radii at -dz
// Rmin2, Rmax2 - inside and outside radii at +dz
//
//--------------------------------------------------------------------------
//
/*
 */
//
//
//
/*
*/
//
//
//
/*
 */
//
//
//
/*
*/
//
//
//
/*
 */
//
//
/*
*/
//
//
/*
 */
//
//--------------------------------------------------------------------------
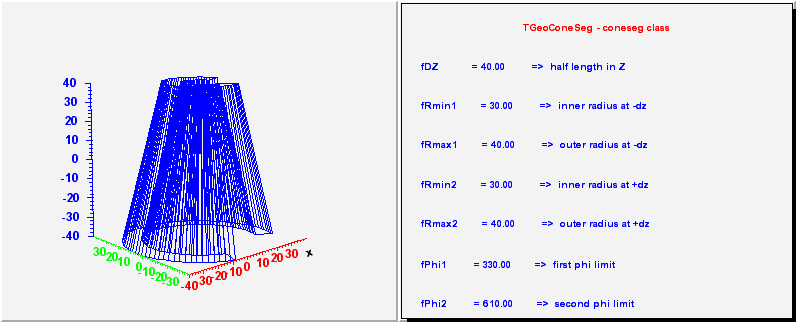
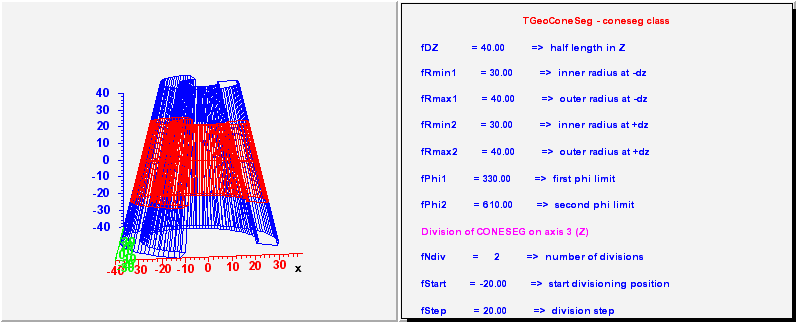
// TGeoConeSeg - a phi segment of a conical tube. Has 7 parameters :
// - the same 5 as a cone;
// - first phi limit (in degrees)
// - second phi limit
//
//--------------------------------------------------------------------------
//
//
/*
*/
//
//--------------------------------------------------------------------------
// TGeoConeSeg - a phi segment of a conical tube. Has 7 parameters :
// - the same 5 as a cone;
// - first phi limit (in degrees)
// - second phi limit
//
//--------------------------------------------------------------------------
//
//
/*
 */
//
//
//
/*
*/
//
//
//
/*
 */
//
#include "Riostream.h"
#include "TROOT.h"
#include "TGeoManager.h"
#include "TGeoVolume.h"
#include "TVirtualGeoPainter.h"
#include "TGeoCone.h"
#include "TVirtualPad.h"
#include "TBuffer3D.h"
#include "TBuffer3DTypes.h"
ClassImp(TGeoCone)
//_____________________________________________________________________________
TGeoCone::TGeoCone()
{
// Default constructor
SetShapeBit(TGeoShape::kGeoCone);
fDz = 0.0;
fRmin1 = 0.0;
fRmax1 = 0.0;
fRmin2 = 0.0;
fRmax2 = 0.0;
}
//_____________________________________________________________________________
TGeoCone::TGeoCone(Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2)
:TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoCone);
SetConeDimensions(dz, rmin1, rmax1, rmin2, rmax2);
if ((dz<0) || (rmin1<0) || (rmax1<0) || (rmin2<0) || (rmax2<0)) {
SetShapeBit(kGeoRunTimeShape);
}
else ComputeBBox();
}
//_____________________________________________________________________________
TGeoCone::TGeoCone(const char *name, Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2)
:TGeoBBox(name, 0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoCone);
SetConeDimensions(dz, rmin1, rmax1, rmin2, rmax2);
if ((dz<0) || (rmin1<0) || (rmax1<0) || (rmin2<0) || (rmax2<0)) {
SetShapeBit(kGeoRunTimeShape);
}
else ComputeBBox();
}
//_____________________________________________________________________________
TGeoCone::TGeoCone(Double_t *param)
:TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
// param[0] = dz
// param[1] = Rmin1
// param[2] = Rmax1
// param[3] = Rmin2
// param[4] = Rmax2
SetShapeBit(TGeoShape::kGeoCone);
SetDimensions(param);
if ((fDz<0) || (fRmin1<0) || (fRmax1<0) || (fRmin2<0) || (fRmax2<0))
SetShapeBit(kGeoRunTimeShape);
else ComputeBBox();
}
//_____________________________________________________________________________
TGeoCone::~TGeoCone()
{
// destructor
}
//_____________________________________________________________________________
void TGeoCone::ComputeBBox()
{
// compute bounding box of the sphere
TGeoBBox *box = (TGeoBBox*)this;
box->SetBoxDimensions(TMath::Max(fRmax1, fRmax2), TMath::Max(fRmax1, fRmax2), fDz);
memset(fOrigin, 0, 3*sizeof(Double_t));
}
//_____________________________________________________________________________
void TGeoCone::ComputeNormal(Double_t *point, Double_t *dir, Double_t *norm)
{
// Compute normal to closest surface from POINT.
Double_t safr,safe,phi;
memset(norm,0,3*sizeof(Double_t));
phi = TMath::ATan2(point[1],point[0]);
Double_t cphi = TMath::Cos(phi);
Double_t sphi = TMath::Sin(phi);
Double_t ro1 = 0.5*(fRmin1+fRmin2);
Double_t tg1 = 0.5*(fRmin2-fRmin1)/fDz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(fRmax1+fRmax2);
Double_t tg2 = 0.5*(fRmax2-fRmax1)/fDz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
safe = TMath::Abs(fDz-TMath::Abs(point[2]));
norm[2] = 1;
safr = (ro1>0)?(TMath::Abs((r-rin)*cr1)):TGeoShape::Big();
if (safr<safe) {
safe = safr;
norm[0] = cr1*cphi;
norm[1] = cr1*sphi;
norm[2] = -tg1*cr1;
}
safr = TMath::Abs((rout-r)*cr2);
if (safr<safe) {
norm[0] = cr2*cphi;
norm[1] = cr2*sphi;
norm[2] = -tg2*cr2;
}
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
void TGeoCone::ComputeNormalS(Double_t *point, Double_t *dir, Double_t *norm,
Double_t dz, Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2)
{
// Compute normal to closest surface from POINT.
Double_t safe,phi;
memset(norm,0,3*sizeof(Double_t));
phi = TMath::ATan2(point[1],point[0]);
Double_t cphi = TMath::Cos(phi);
Double_t sphi = TMath::Sin(phi);
Double_t ro1 = 0.5*(rmin1+rmin2);
Double_t tg1 = 0.5*(rmin2-rmin1)/dz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(rmax1+rmax2);
Double_t tg2 = 0.5*(rmax2-rmax1)/dz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
safe = (ro1>0)?(TMath::Abs((r-rin)*cr1)):TGeoShape::Big();
norm[0] = cr1*cphi;
norm[1] = cr1*sphi;
norm[2] = -tg1*cr1;
if (TMath::Abs((rout-r)*cr2)<safe) {
norm[0] = cr2*cphi;
norm[1] = cr2*sphi;
norm[2] = -tg2*cr2;
}
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
Bool_t TGeoCone::Contains(Double_t *point) const
{
// test if point is inside this cone
if (TMath::Abs(point[2]) > fDz) return kFALSE;
Double_t r2 = point[0]*point[0]+point[1]*point[1];
Double_t rl = 0.5*(fRmin2*(point[2]+fDz)+fRmin1*(fDz-point[2]))/fDz;
Double_t rh = 0.5*(fRmax2*(point[2]+fDz)+fRmax1*(fDz-point[2]))/fDz;
if ((r2<rl*rl) || (r2>rh*rh)) return kFALSE;
return kTRUE;
}
//_____________________________________________________________________________
Double_t TGeoCone::DistFromInsideS(Double_t *point, Double_t *dir, Double_t dz,
Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2)
{
// Compute distance from inside point to surface of the cone (static)
// Boundary safe algorithm.
if (dz<=0) return TGeoShape::Big();
// compute distance to surface
// Do Z
Double_t sz = TGeoShape::Big();
if (dir[2]) {
sz = (TMath::Sign(dz, dir[2])-point[2])/dir[2];
if (sz<=0) return 0.0;
}
Double_t rsq=point[0]*point[0]+point[1]*point[1];
Double_t zinv = 1./dz;
Double_t rin = 0.5*(rmin1+rmin2+(rmin2-rmin1)*point[2]*zinv);
// Do Rmin
Double_t sr = TGeoShape::Big();
Double_t b,delta,zi;
if (rin>0) {
// Protection in case point is actually outside the cone
if (rsq < rin*(rin+TGeoShape::Tolerance())) {
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]+0.5*(rmin1-rmin2)*dir[2]*zinv*TMath::Sqrt(rsq);
if (ddotn<=0) return 0.0;
} else {
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta>0) {
sr = -b-delta;
if (sr>0) {
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
}
sr = -b+delta;
if (sr>0) {
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
}
}
}
}
// Do Rmax
Double_t rout = 0.5*(rmax1+rmax2+(rmax2-rmax1)*point[2]*zinv);
if (rsq > rout*(rout-TGeoShape::Tolerance())) {
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]+0.5*(rmax1-rmax2)*dir[2]*zinv*TMath::Sqrt(rsq);
if (ddotn>=0) return 0.0;
TGeoCone::DistToCone(point, dir, dz, rmax1, rmax2, b, delta);
if (delta<0) return 0.0;
sr = -b+delta;
if (sr<0) return sz;
if (TMath::Abs(-b-delta)>sr) return sz;
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
return sz;
}
TGeoCone::DistToCone(point, dir, dz, rmax1, rmax2, b, delta);
if (delta>0) {
sr = -b-delta;
if (sr>0) {
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
}
sr = -b+delta;
if (sr>TGeoShape::Tolerance()) {
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
}
}
return sz;
}
//_____________________________________________________________________________
Double_t TGeoCone::DistFromInside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// Compute distance from inside point to surface of the cone
// Boundary safe algorithm.
if (iact<3 && safe) {
*safe = Safety(point, kTRUE);
if (iact==0) return TGeoShape::Big();
if ((iact==1) && (*safe>step)) return TGeoShape::Big();
}
// compute distance to surface
return TGeoCone::DistFromInsideS(point, dir, fDz, fRmin1, fRmax1, fRmin2, fRmax2);
}
//_____________________________________________________________________________
Double_t TGeoCone::DistFromOutsideS(Double_t *point, Double_t *dir, Double_t dz,
Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2)
{
// Compute distance from outside point to surface of the tube
// Boundary safe algorithm.
// compute distance to Z planes
if (dz<=0) return TGeoShape::Big();
Double_t snxt;
Double_t xp, yp, zp;
Bool_t inz = kTRUE;
if (point[2]<=-dz) {
if (dir[2]<=0) return TGeoShape::Big();
snxt = (-dz-point[2])/dir[2];
xp = point[0]+snxt*dir[0];
yp = point[1]+snxt*dir[1];
Double_t r2 = xp*xp+yp*yp;
if ((r2>=rmin1*rmin1) && (r2<=rmax1*rmax1)) return snxt;
inz = kFALSE;
} else {
if (point[2]>=dz) {
if (dir[2]>=0) return TGeoShape::Big();
snxt = (dz-point[2])/dir[2];
xp = point[0]+snxt*dir[0];
yp = point[1]+snxt*dir[1];
Double_t r2 = xp*xp+yp*yp;
if ((r2>=rmin2*rmin2) && (r2<=rmax2*rmax2)) return snxt;
inz = kFALSE;
}
}
Double_t rsq = point[0]*point[0]+point[1]*point[1];
Double_t dzinv = 1./dz;
Double_t ro1=0.5*(rmin1+rmin2);
Bool_t hasrmin = (ro1>0)?kTRUE:kFALSE;
Double_t tg1 = 0.;
Double_t rin = 0.;
Bool_t inrmin = kTRUE; // r>=rmin
if (hasrmin) {
tg1=0.5*(rmin2-rmin1)*dzinv;
rin=ro1+tg1*point[2];
if (rin>0 && rsq<rin*(rin-TGeoShape::Tolerance())) inrmin=kFALSE;
}
Double_t ro2=0.5*(rmax1+rmax2);
Double_t tg2=0.5*(rmax2-rmax1)*dzinv;
Double_t rout=tg2*point[2]+ro2;
Bool_t inrmax = kFALSE;
if (rout>0 && rsq<rout*(rout+TGeoShape::Tolerance())) inrmax=kTRUE;
Bool_t in = inz & inrmin & inrmax;
Double_t b,delta;
// If inside cone, we are most likely on a boundary within machine precision.
if (in) {
Double_t r=TMath::Sqrt(rsq);
Double_t safz = dz-TMath::Abs(point[2]); // positive
Double_t safrmin = (hasrmin)?(r-rin):TGeoShape::Big();
Double_t safrmax = rout - r;
if (safz<=safrmin && safz<=safrmax) {
// on Z boundary
if (point[2]*dir[2]<0) return 0.0;
return TGeoShape::Big();
}
if (safrmax<safrmin) {
// on rmax boundary
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg2*dir[2]*r;
if (ddotn<=0) return 0.0;
return TGeoShape::Big();
}
// on rmin boundary
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg1*dir[2]*r;
if (ddotn>=0) return 0.0;
// we can cross (+) solution of rmin
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta<0) return 0.0;
snxt = -b+delta;
if (snxt<0) return TGeoShape::Big();
if (TMath::Abs(-b-delta)>snxt) return TGeoShape::Big();
zp = point[2]+snxt*dir[2];
if (TMath::Abs(zp)<=dz) return snxt;
return TGeoShape::Big();
}
// compute distance to inner cone
snxt = TGeoShape::Big();
if (!inrmin) {
// ray can cross only inner cone
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta<0) return TGeoShape::Big();
snxt = -b+delta;
if (snxt<=0) return TGeoShape::Big();
zp = point[2]+snxt*dir[2];
if (TMath::Abs(zp)<=dz) return snxt;
snxt = -b-delta;
if (snxt<=0) return TGeoShape::Big();
zp = point[2]+snxt*dir[2];
if (TMath::Abs(zp)<=dz) return snxt;
return TGeoShape::Big();
} else {
if (hasrmin) {
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta>0) {
Double_t din = -b+delta;
if (din>0) {
zp = point[2]+din*dir[2];
if (TMath::Abs(zp)<=dz) snxt = din;
}
}
}
}
if (inrmax) return snxt;
// we can cross only outer cone, both solutions possible
// compute distance to outer cone
TGeoCone::DistToCone(point, dir, dz, rmax1, rmax2, b, delta);
if (delta<0) return snxt;
Double_t dout = -b-delta;
if (dout>0 && dout<snxt) {
zp = point[2]+dout*dir[2];
if (TMath::Abs(zp)<=dz) return dout;
}
dout = -b+delta;
if (dout<=0 || dout>snxt) return snxt;
zp = point[2]+dout*dir[2];
if (TMath::Abs(zp)<=dz) return dout;
return snxt;
}
//_____________________________________________________________________________
Double_t TGeoCone::DistFromOutside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from outside point to surface of the tube
// compute safe radius
if (iact<3 && safe) {
*safe = Safety(point, kFALSE);
if (iact==0) return TGeoShape::Big();
if ((iact==1) && (*safe>step)) return TGeoShape::Big();
}
// compute distance to Z planes
return TGeoCone::DistFromOutsideS(point, dir, fDz, fRmin1, fRmax1, fRmin2, fRmax2);
}
//_____________________________________________________________________________
void TGeoCone::DistToCone(Double_t *point, Double_t *dir, Double_t dz, Double_t r1, Double_t r2,
Double_t &b, Double_t &delta)
{
// Static method to compute distance to a conical surface with :
// - r1, z1 - radius and Z position of lower base
// - r2, z2 - radius and Z position of upper base
delta = -1.;
if (dz<0) return;
Double_t ro0 = 0.5*(r1+r2);
Double_t tz = 0.5*(r2-r1)/dz;
Double_t rsq = point[0]*point[0] + point[1]*point[1];
Double_t rc = ro0 + point[2]*tz;
Double_t a = dir[0]*dir[0] + dir[1]*dir[1] - tz*tz*dir[2]*dir[2];
b = point[0]*dir[0] + point[1]*dir[1] - tz*rc*dir[2];
Double_t c = rsq - rc*rc;
if (a==0) {
if (b==0) return;
b = 0.5*c/b;
return;
}
a = 1./a;
b *= a;
c *= a;
delta = b*b - c;
if (delta>0) {
delta = TMath::Sqrt(delta);
} else {
delta = -1.;
}
}
//_____________________________________________________________________________
Int_t TGeoCone::DistancetoPrimitive(Int_t px, Int_t py)
{
// compute closest distance from point px,py to each corner
Int_t n = gGeoManager->GetNsegments();
const Int_t numPoints = 4*n;
return ShapeDistancetoPrimitive(numPoints, px, py);
}
//_____________________________________________________________________________
TGeoVolume *TGeoCone::Divide(TGeoVolume *voldiv, const char *divname, Int_t iaxis, Int_t ndiv,
Double_t start, Double_t step)
{
//--- Divide this cone shape belonging to volume "voldiv" into ndiv volumes
// called divname, from start position with the given step. Returns pointer
// to created division cell volume in case of Z divisions. For Z division
// creates all volumes with different shapes and returns pointer to volume that
// was divided. In case a wrong division axis is supplied, returns pointer to
// volume that was divided.
TGeoShape *shape; //--- shape to be created
TGeoVolume *vol; //--- division volume to be created
TGeoVolumeMulti *vmulti; //--- generic divided volume
TGeoPatternFinder *finder; //--- finder to be attached
TString opt = ""; //--- option to be attached
Int_t id;
Double_t end = start+ndiv*step;
switch (iaxis) {
case 1: //--- R division
Error("Divide","division of a cone on R not implemented");
return 0;
case 2: // --- Phi division
finder = new TGeoPatternCylPhi(voldiv, ndiv, start, end);
voldiv->SetFinder(finder);
finder->SetDivIndex(voldiv->GetNdaughters());
shape = new TGeoConeSeg(fDz, fRmin1, fRmax1, fRmin2, fRmax2, -step/2, step/2);
vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
vmulti->AddVolume(vol);
opt = "Phi";
for (id=0; id<ndiv; id++) {
voldiv->AddNodeOffset(vol, id, start+id*step+step/2, opt.Data());
((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);
}
return vmulti;
case 3: //--- Z division
vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
finder = new TGeoPatternZ(voldiv, ndiv, start, end);
voldiv->SetFinder(finder);
finder->SetDivIndex(voldiv->GetNdaughters());
for (id=0; id<ndiv; id++) {
Double_t z1 = start+id*step;
Double_t z2 = start+(id+1)*step;
Double_t rmin1n = 0.5*(fRmin1*(fDz-z1)+fRmin2*(fDz+z1))/fDz;
Double_t rmax1n = 0.5*(fRmax1*(fDz-z1)+fRmax2*(fDz+z1))/fDz;
Double_t rmin2n = 0.5*(fRmin1*(fDz-z2)+fRmin2*(fDz+z2))/fDz;
Double_t rmax2n = 0.5*(fRmax1*(fDz-z2)+fRmax2*(fDz+z2))/fDz;
shape = new TGeoCone(0.5*step,rmin1n, rmax1n, rmin2n, rmax2n);
vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
vmulti->AddVolume(vol);
opt = "Z";
voldiv->AddNodeOffset(vol, id, start+id*step+step/2, opt.Data());
((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);
}
return vmulti;
default:
Error("Divide", "Wrong axis type for division");
return 0;
}
}
//_____________________________________________________________________________
const char *TGeoCone::GetAxisName(Int_t iaxis) const
{
// Returns name of axis IAXIS.
switch (iaxis) {
case 1:
return "R";
case 2:
return "PHI";
case 3:
return "Z";
default:
return "undefined";
}
}
//_____________________________________________________________________________
Double_t TGeoCone::GetAxisRange(Int_t iaxis, Double_t &xlo, Double_t &xhi) const
{
// Get range of shape for a given axis.
xlo = 0;
xhi = 0;
Double_t dx = 0;
switch (iaxis) {
case 2:
xlo = 0.;
xhi = 360.;
return 360.;
case 3:
xlo = -fDz;
xhi = fDz;
dx = xhi-xlo;
return dx;
}
return dx;
}
//_____________________________________________________________________________
void TGeoCone::GetBoundingCylinder(Double_t *param) const
{
//--- Fill vector param[4] with the bounding cylinder parameters. The order
// is the following : Rmin, Rmax, Phi1, Phi2, dZ
param[0] = TMath::Min(fRmin1, fRmin2); // Rmin
param[0] *= param[0];
param[1] = TMath::Max(fRmax1, fRmax2); // Rmax
param[1] *= param[1];
param[2] = 0.; // Phi1
param[3] = 360.; // Phi1
}
//_____________________________________________________________________________
TGeoShape *TGeoCone::GetMakeRuntimeShape(TGeoShape *mother, TGeoMatrix * /*mat*/) const
{
// in case shape has some negative parameters, these has to be computed
// in order to fit the mother
if (!TestShapeBit(kGeoRunTimeShape)) return 0;
if (!mother->TestShapeBit(kGeoCone)) {
Error("GetMakeRuntimeShape", "invalid mother");
return 0;
}
Double_t rmin1, rmax1, rmin2, rmax2, dz;
rmin1 = fRmin1;
rmax1 = fRmax1;
rmin2 = fRmin2;
rmax2 = fRmax2;
dz = fDz;
if (fDz<0) dz=((TGeoCone*)mother)->GetDz();
if (fRmin1<0)
rmin1 = ((TGeoCone*)mother)->GetRmin1();
if (fRmax1<0)
rmax1 = ((TGeoCone*)mother)->GetRmax1();
if (fRmin2<0)
rmin2 = ((TGeoCone*)mother)->GetRmin2();
if (fRmax2<0)
rmax2 = ((TGeoCone*)mother)->GetRmax2();
return (new TGeoCone(GetName(), dz, rmin1, rmax1, rmin2, rmax2));
}
//_____________________________________________________________________________
void TGeoCone::InspectShape() const
{
// print shape parameters
printf("*** Shape %s TGeoCone ***\n", GetName());
printf(" dz =: %11.5f\n", fDz);
printf(" Rmin1 = %11.5f\n", fRmin1);
printf(" Rmax1 = %11.5f\n", fRmax1);
printf(" Rmin2 = %11.5f\n", fRmin2);
printf(" Rmax2 = %11.5f\n", fRmax2);
printf(" Bounding box:\n");
TGeoBBox::InspectShape();
}
//_____________________________________________________________________________
TBuffer3D *TGeoCone::MakeBuffer3D() const
{
// Creates a TBuffer3D describing *this* shape.
// Coordinates are in local reference frame.
Int_t n = gGeoManager->GetNsegments();
Int_t nbPnts = 4*n;
Int_t nbSegs = 8*n;
Int_t nbPols = 4*n;
TBuffer3D* buff = new TBuffer3D(TBuffer3DTypes::kGeneric,
nbPnts, 3*nbPnts,
nbSegs, 3*nbSegs,
nbPols, 6*nbPols);
if (buff)
{
SetPoints(buff->fPnts);
SetSegsAndPols(*buff);
}
return buff;
}
//_____________________________________________________________________________
void TGeoCone::SetSegsAndPols(TBuffer3D &buffer) const
{
// Fill TBuffer3D structure for segments and polygons.
Int_t i,j;
Int_t n = gGeoManager->GetNsegments();
Int_t c = GetBasicColor();
for (i = 0; i < 4; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c;
buffer.fSegs[(i*n+j)*3+1] = i*n+j;
buffer.fSegs[(i*n+j)*3+2] = i*n+j+1;
}
buffer.fSegs[(i*n+j-1)*3+2] = i*n;
}
for (i = 4; i < 6; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c+1;
buffer.fSegs[(i*n+j)*3+1] = (i-4)*n+j;
buffer.fSegs[(i*n+j)*3+2] = (i-2)*n+j;
}
}
for (i = 6; i < 8; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c;
buffer.fSegs[(i*n+j)*3+1] = 2*(i-6)*n+j;
buffer.fSegs[(i*n+j)*3+2] = (2*(i-6)+1)*n+j;
}
}
Int_t indx = 0;
i=0;
for (j = 0; j < n; j++) {
indx = 6*(i*n+j);
buffer.fPols[indx ] = c;
buffer.fPols[indx+1] = 4;
buffer.fPols[indx+5] = i*n+j;
buffer.fPols[indx+4] = (4+i)*n+j;
buffer.fPols[indx+3] = (2+i)*n+j;
buffer.fPols[indx+2] = (4+i)*n+j+1;
}
buffer.fPols[indx+2] = (4+i)*n;
i=1;
for (j = 0; j < n; j++) {
indx = 6*(i*n+j);
buffer.fPols[indx ] = c;
buffer.fPols[indx+1] = 4;
buffer.fPols[indx+2] = i*n+j;
buffer.fPols[indx+3] = (4+i)*n+j;
buffer.fPols[indx+4] = (2+i)*n+j;
buffer.fPols[indx+5] = (4+i)*n+j+1;
}
buffer.fPols[indx+5] = (4+i)*n;
i=2;
for (j = 0; j < n; j++) {
indx = 6*(i*n+j);
buffer.fPols[indx ] = c+i;
buffer.fPols[indx+1] = 4;
buffer.fPols[indx+2] = (i-2)*2*n+j;
buffer.fPols[indx+3] = (4+i)*n+j;
buffer.fPols[indx+4] = ((i-2)*2+1)*n+j;
buffer.fPols[indx+5] = (4+i)*n+j+1;
}
buffer.fPols[indx+5] = (4+i)*n;
i=3;
for (j = 0; j < n; j++) {
indx = 6*(i*n+j);
buffer.fPols[indx ] = c+i;
buffer.fPols[indx+1] = 4;
buffer.fPols[indx+5] = (i-2)*2*n+j;
buffer.fPols[indx+4] = (4+i)*n+j;
buffer.fPols[indx+3] = ((i-2)*2+1)*n+j;
buffer.fPols[indx+2] = (4+i)*n+j+1;
}
buffer.fPols[indx+2] = (4+i)*n;
}
//_____________________________________________________________________________
Double_t TGeoCone::Safety(Double_t *point, Bool_t in) const
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
Double_t saf[3];
Double_t ro1 = 0.5*(fRmin1+fRmin2);
Double_t tg1 = 0.5*(fRmin2-fRmin1)/fDz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(fRmax1+fRmax2);
Double_t tg2 = 0.5*(fRmax2-fRmax1)/fDz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
saf[0] = fDz-TMath::Abs(point[2]);
saf[1] = (ro1>0)?((r-rin)*cr1):TGeoShape::Big();
saf[2] = (rout-r)*cr2;
if (in) return saf[TMath::LocMin(3,saf)];
for (Int_t i=0; i<3; i++) saf[i]=-saf[i];
return saf[TMath::LocMax(3,saf)];
}
//_____________________________________________________________________________
Double_t TGeoCone::SafetyS(Double_t *point, Bool_t in, Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Int_t skipz)
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
Double_t saf[3];
Double_t ro1 = 0.5*(rmin1+rmin2);
Double_t tg1 = 0.5*(rmin2-rmin1)/dz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(rmax1+rmax2);
Double_t tg2 = 0.5*(rmax2-rmax1)/dz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
switch (skipz) {
case 1: // skip lower Z plane
saf[0] = dz - point[2];
break;
case 2: // skip upper Z plane
saf[0] = dz + point[2];
break;
case 3: // skip both
saf[0] = TGeoShape::Big();
break;
default:
saf[0] = dz-TMath::Abs(point[2]);
}
saf[1] = (ro1>0)?((r-rin)*cr1):TGeoShape::Big();
saf[2] = (rout-r)*cr2;
if (in) return saf[TMath::LocMin(3,saf)];
for (Int_t i=0; i<3; i++) saf[i]=-saf[i];
return saf[TMath::LocMax(3,saf)];
}
//_____________________________________________________________________________
void TGeoCone::SavePrimitive(ofstream &out, Option_t * /*option*/)
{
// Save a primitive as a C++ statement(s) on output stream "out".
if (TObject::TestBit(kGeoSavePrimitive)) return;
out << " // Shape: " << GetName() << " type: " << ClassName() << endl;
out << " dz = " << fDz << ";" << endl;
out << " rmin1 = " << fRmin1 << ";" << endl;
out << " rmax1 = " << fRmax1 << ";" << endl;
out << " rmin2 = " << fRmin2 << ";" << endl;
out << " rmax2 = " << fRmax2 << ";" << endl;
out << " TGeoShape *" << GetPointerName() << " = new TGeoCone(\"" << GetName() << "\", dz,rmin1,rmax1,rmin2,rmax2);" << endl;
TObject::SetBit(TGeoShape::kGeoSavePrimitive);
}
//_____________________________________________________________________________
void TGeoCone::SetConeDimensions(Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2)
{
if (rmin1>=0) {
if (rmax1>0) {
if (rmin1<=rmax1) {
// normal rmin/rmax
fRmin1 = rmin1;
fRmax1 = rmax1;
} else {
fRmin1 = rmax1;
fRmax1 = rmin1;
Warning("SetConeDimensions", "rmin1>rmax1 Switch rmin1<->rmax1");
SetShapeBit(TGeoShape::kGeoBad);
}
} else {
// run-time
fRmin1 = rmin1;
fRmax1 = rmax1;
}
} else {
// run-time
fRmin1 = rmin1;
fRmax1 = rmax1;
}
if (rmin2>=0) {
if (rmax2>0) {
if (rmin2<=rmax2) {
// normal rmin/rmax
fRmin2 = rmin2;
fRmax2 = rmax2;
} else {
fRmin2 = rmax2;
fRmax2 = rmin2;
Warning("SetConeDimensions", "rmin2>rmax2 Switch rmin2<->rmax2");
SetShapeBit(TGeoShape::kGeoBad);
}
} else {
// run-time
fRmin2 = rmin2;
fRmax2 = rmax2;
}
} else {
// run-time
fRmin2 = rmin2;
fRmax2 = rmax2;
}
fDz = dz;
}
//_____________________________________________________________________________
void TGeoCone::SetDimensions(Double_t *param)
{
Double_t dz = param[0];
Double_t rmin1 = param[1];
Double_t rmax1 = param[2];
Double_t rmin2 = param[3];
Double_t rmax2 = param[4];
SetConeDimensions(dz, rmin1, rmax1, rmin2, rmax2);
}
//_____________________________________________________________________________
void TGeoCone::SetPoints(Double_t *points) const
{
// create cone mesh points
Double_t dz, phi, dphi;
Int_t j, n;
n = gGeoManager->GetNsegments();
dphi = 360./n;
dz = fDz;
Int_t indx = 0;
if (points) {
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmin1 * TMath::Cos(phi);
points[indx++] = fRmin1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmax1 * TMath::Cos(phi);
points[indx++] = fRmax1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmin2 * TMath::Cos(phi);
points[indx++] = fRmin2 * TMath::Sin(phi);
points[indx++] = dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmax2 * TMath::Cos(phi);
points[indx++] = fRmax2 * TMath::Sin(phi);
points[indx++] = dz;
}
}
}
//_____________________________________________________________________________
void TGeoCone::SetPoints(Float_t *points) const
{
// create cone mesh points
Double_t dz, phi, dphi;
Int_t j, n;
n = gGeoManager->GetNsegments();
dphi = 360./n;
dz = fDz;
Int_t indx = 0;
if (points) {
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmin1 * TMath::Cos(phi);
points[indx++] = fRmin1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmax1 * TMath::Cos(phi);
points[indx++] = fRmax1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmin2 * TMath::Cos(phi);
points[indx++] = fRmin2 * TMath::Sin(phi);
points[indx++] = dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmax2 * TMath::Cos(phi);
points[indx++] = fRmax2 * TMath::Sin(phi);
points[indx++] = dz;
}
}
}
//_____________________________________________________________________________
Int_t TGeoCone::GetNmeshVertices() const
{
// Return number of vertices of the mesh representation
Int_t n = gGeoManager->GetNsegments();
Int_t numPoints = n*4;
return numPoints;
}
//_____________________________________________________________________________
void TGeoCone::Sizeof3D() const
{
///// fill size of this 3-D object
/// TVirtualGeoPainter *painter = gGeoManager->GetGeomPainter();
/// if (!painter) return;
/// Int_t n = gGeoManager->GetNsegments();
/// Int_t numPoints = n*4;
/// Int_t numSegs = n*8;
/// Int_t numPolys = n*4;
/// painter->AddSize3D(numPoints, numSegs, numPolys);
}
//_____________________________________________________________________________
const TBuffer3D & TGeoCone::GetBuffer3D(Int_t reqSections, Bool_t localFrame) const
{
static TBuffer3D buffer(TBuffer3DTypes::kGeneric);
TGeoBBox::FillBuffer3D(buffer, reqSections, localFrame);
if (reqSections & TBuffer3D::kRawSizes) {
Int_t n = gGeoManager->GetNsegments();
Int_t nbPnts = 4*n;
Int_t nbSegs = 8*n;
Int_t nbPols = 4*n;
if (buffer.SetRawSizes(nbPnts, 3*nbPnts, nbSegs, 3*nbSegs, nbPols, 6*nbPols)) {
buffer.SetSectionsValid(TBuffer3D::kRawSizes);
}
}
// TODO: Can we push this as common down to TGeoShape?
if ((reqSections & TBuffer3D::kRaw) && buffer.SectionsValid(TBuffer3D::kRawSizes)) {
SetPoints(buffer.fPnts);
if (!buffer.fLocalFrame) {
TransformPoints(buffer.fPnts, buffer.NbPnts());
}
SetSegsAndPols(buffer);
buffer.SetSectionsValid(TBuffer3D::kRaw);
}
return buffer;
}
ClassImp(TGeoConeSeg)
//_____________________________________________________________________________
TGeoConeSeg::TGeoConeSeg()
{
// Default constructor
SetShapeBit(TGeoShape::kGeoConeSeg);
fPhi1 = fPhi2 = 0.0;
}
//_____________________________________________________________________________
TGeoConeSeg::TGeoConeSeg(Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Double_t phi1, Double_t phi2)
:TGeoCone(dz, rmin1, rmax1, rmin2, rmax2)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoConeSeg);
SetConsDimensions(dz, rmin1, rmax1, rmin2, rmax2, phi1, phi2);
ComputeBBox();
}
//_____________________________________________________________________________
TGeoConeSeg::TGeoConeSeg(const char *name, Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Double_t phi1, Double_t phi2)
:TGeoCone(name, dz, rmin1, rmax1, rmin2, rmax2)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoConeSeg);
SetConsDimensions(dz, rmin1, rmax1, rmin2, rmax2, phi1, phi2);
ComputeBBox();
}
//_____________________________________________________________________________
TGeoConeSeg::TGeoConeSeg(Double_t *param)
:TGeoCone(0,0,0,0,0)
{
// Default constructor specifying minimum and maximum radius
// param[0] = dz
// param[1] = Rmin1
// param[2] = Rmax1
// param[3] = Rmin2
// param[4] = Rmax2
// param[5] = phi1
// param[6] = phi2
SetShapeBit(TGeoShape::kGeoConeSeg);
SetDimensions(param);
ComputeBBox();
}
//_____________________________________________________________________________
TGeoConeSeg::~TGeoConeSeg()
{
// destructor
}
//_____________________________________________________________________________
void TGeoConeSeg::ComputeBBox()
{
// compute bounding box of the tube segment
Double_t rmin, rmax;
rmin = TMath::Min(fRmin1, fRmin2);
rmax = TMath::Max(fRmax1, fRmax2);
Double_t xc[4];
Double_t yc[4];
xc[0] = rmax*TMath::Cos(fPhi1*TMath::DegToRad());
yc[0] = rmax*TMath::Sin(fPhi1*TMath::DegToRad());
xc[1] = rmax*TMath::Cos(fPhi2*TMath::DegToRad());
yc[1] = rmax*TMath::Sin(fPhi2*TMath::DegToRad());
xc[2] = rmin*TMath::Cos(fPhi1*TMath::DegToRad());
yc[2] = rmin*TMath::Sin(fPhi1*TMath::DegToRad());
xc[3] = rmin*TMath::Cos(fPhi2*TMath::DegToRad());
yc[3] = rmin*TMath::Sin(fPhi2*TMath::DegToRad());
Double_t xmin = xc[TMath::LocMin(4, &xc[0])];
Double_t xmax = xc[TMath::LocMax(4, &xc[0])];
Double_t ymin = yc[TMath::LocMin(4, &yc[0])];
Double_t ymax = yc[TMath::LocMax(4, &yc[0])];
Double_t dp = fPhi2-fPhi1;
Double_t ddp = -fPhi1;
if (ddp<0) ddp+= 360;
if (ddp<=dp) xmax = rmax;
ddp = 90-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp<=dp) ymax = rmax;
ddp = 180-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp<=dp) xmin = -rmax;
ddp = 270-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp<=dp) ymin = -rmax;
fOrigin[0] = (xmax+xmin)/2;
fOrigin[1] = (ymax+ymin)/2;
fOrigin[2] = 0;
fDX = (xmax-xmin)/2;
fDY = (ymax-ymin)/2;
fDZ = fDz;
}
//_____________________________________________________________________________
void TGeoConeSeg::ComputeNormal(Double_t *point, Double_t *dir, Double_t *norm)
{
// Compute normal to closest surface from POINT.
Double_t saf[3];
Double_t ro1 = 0.5*(fRmin1+fRmin2);
Double_t tg1 = 0.5*(fRmin2-fRmin1)/fDz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(fRmax1+fRmax2);
Double_t tg2 = 0.5*(fRmax2-fRmax1)/fDz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t c1 = TMath::Cos(fPhi1*TMath::DegToRad());
Double_t s1 = TMath::Sin(fPhi1*TMath::DegToRad());
Double_t c2 = TMath::Cos(fPhi2*TMath::DegToRad());
Double_t s2 = TMath::Sin(fPhi2*TMath::DegToRad());
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
saf[0] = TMath::Abs(fDz-TMath::Abs(point[2]));
saf[1] = (ro1>0)?(TMath::Abs((r-rin)*cr1)):TGeoShape::Big();
saf[2] = TMath::Abs((rout-r)*cr2);
Int_t i = TMath::LocMin(3,saf);
if (TGeoShape::IsCloseToPhi(saf[i], point,c1,s1,c2,s2)) {
TGeoShape::NormalPhi(point,dir,norm,c1,s1,c2,s2);
return;
}
if (i==0) {
norm[0] = norm[1] = 0.;
norm[2] = TMath::Sign(1.,dir[2]);
return;
}
Double_t phi = TMath::ATan2(point[1],point[0]);
Double_t cphi = TMath::Cos(phi);
Double_t sphi = TMath::Sin(phi);
if (i==1) {
norm[0] = cr1*cphi;
norm[1] = cr1*sphi;
norm[2] = -tg1*cr1;
} else {
norm[0] = cr2*cphi;
norm[1] = cr2*sphi;
norm[2] = -tg2*cr2;
}
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
void TGeoConeSeg::ComputeNormalS(Double_t *point, Double_t *dir, Double_t *norm,
Double_t dz, Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2,
Double_t c1, Double_t s1, Double_t c2, Double_t s2)
{
// Compute normal to closest surface from POINT.
Double_t saf[2];
Double_t ro1 = 0.5*(rmin1+rmin2);
Double_t tg1 = 0.5*(rmin2-rmin1)/dz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(rmax1+rmax2);
Double_t tg2 = 0.5*(rmax2-rmax1)/dz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
saf[0] = (ro1>0)?(TMath::Abs((r-rin)*cr1)):TGeoShape::Big();
saf[1] = TMath::Abs((rout-r)*cr2);
Int_t i = TMath::LocMin(2,saf);
if (TGeoShape::IsCloseToPhi(saf[i], point,c1,s1,c2,s2)) {
TGeoShape::NormalPhi(point,dir,norm,c1,s1,c2,s2);
return;
}
Double_t phi = TMath::ATan2(point[1],point[0]);
Double_t cphi = TMath::Cos(phi);
Double_t sphi = TMath::Sin(phi);
if (i==0) {
norm[0] = cr1*cphi;
norm[1] = cr1*sphi;
norm[2] = -tg1*cr1;
} else {
norm[0] = cr2*cphi;
norm[1] = cr2*sphi;
norm[2] = -tg2*cr2;
}
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
Bool_t TGeoConeSeg::Contains(Double_t *point) const
{
// test if point is inside this sphere
if (!TGeoCone::Contains(point)) return kFALSE;
Double_t phi = TMath::ATan2(point[1], point[0]) * TMath::RadToDeg();
if (phi < 0 ) phi+=360.;
Double_t dphi = fPhi2 - fPhi1;
Double_t ddp = phi-fPhi1;
if (ddp < 0) ddp+=360.;
// if (ddp > 360) ddp-=360;
if (ddp > dphi) return kFALSE;
return kTRUE;
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistToCons(Double_t *point, Double_t *dir, Double_t r1, Double_t z1, Double_t r2, Double_t z2, Double_t phi1, Double_t phi2)
{
// Static method to compute distance to a conical surface with :
// - r1, z1 - radius and Z position of lower base
// - r2, z2 - radius and Z position of upper base
// - phi1, phi2 - phi limits
Double_t dz = z2-z1;
if (dz<=0) {
return TGeoShape::Big();
}
Double_t dphi = phi2 - phi1;
if (dphi < 0) dphi+=360.;
// printf("phi1=%f phi2=%f dphi=%f\n", phi1, phi2, dphi);
Double_t ro0 = 0.5*(r1+r2);
Double_t fz = (r2-r1)/dz;
Double_t r0sq = point[0]*point[0] + point[1]*point[1];
Double_t rc = ro0 + fz*(point[2]-0.5*(z1+z2));
Double_t a = dir[0]*dir[0] + dir[1]*dir[1] - fz*fz*dir[2]*dir[2];
Double_t b = point[0]*dir[0] + point[1]*dir[1] - fz*rc*dir[2];
Double_t c = r0sq - rc*rc;
if (a==0) return TGeoShape::Big();
a = 1./a;
b *= a;
c *= a;
Double_t delta = b*b - c;
if (delta<0) return TGeoShape::Big();
delta = TMath::Sqrt(delta);
Double_t snxt = -b-delta;
Double_t ptnew[3];
Double_t ddp, phi;
if (snxt>0) {
// check Z range
ptnew[2] = point[2] + snxt*dir[2];
if (((ptnew[2]-z1)*(ptnew[2]-z2)) < 0) {
// check phi range
ptnew[0] = point[0] + snxt*dir[0];
ptnew[1] = point[1] + snxt*dir[1];
phi = TMath::ATan2(ptnew[1], ptnew[0]) * TMath::RadToDeg();
if (phi < 0 ) phi+=360.;
ddp = phi-phi1;
if (ddp < 0) ddp+=360.;
// printf("snxt1=%f phi=%f ddp=%f\n", snxt, phi, ddp);
if (ddp<=dphi) return snxt;
}
}
snxt = -b+delta;
if (snxt>0) {
// check Z range
ptnew[2] = point[2] + snxt*dir[2];
if (((ptnew[2]-z1)*(ptnew[2]-z2)) < 0) {
// check phi range
ptnew[0] = point[0] + snxt*dir[0];
ptnew[1] = point[1] + snxt*dir[1];
phi = TMath::ATan2(ptnew[1], ptnew[0]) * TMath::RadToDeg();
if (phi < 0 ) phi+=360.;
ddp = phi-phi1;
if (ddp < 0) ddp+=360.;
// printf("snxt2=%f phi=%f ddp=%f\n", snxt, phi, ddp);
if (ddp<=dphi) return snxt;
}
}
return TGeoShape::Big();
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistFromInsideS(Double_t *point, Double_t *dir, Double_t dz,
Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2,
Double_t c1, Double_t s1, Double_t c2, Double_t s2, Double_t cm, Double_t sm, Double_t cdfi)
{
// compute distance from inside point to surface of the tube segment
if (dz<=0) return TGeoShape::Big();
// Do Z
Double_t scone = TGeoCone::DistFromInsideS(point,dir,dz,rmin1,rmax1,rmin2,rmax2);
if (scone<=0) return 0.0;
Double_t sfmin = TGeoShape::Big();
Double_t rsq = point[0]*point[0]+point[1]*point[1];
Double_t r = TMath::Sqrt(rsq);
Double_t cpsi=point[0]*cm+point[1]*sm;
if (cpsi>r*cdfi+TGeoShape::Tolerance()) {
sfmin = TGeoShape::DistToPhiMin(point, dir, s1, c1, s2, c2, sm, cm);
return TMath::Min(scone,sfmin);
}
// Point on the phi boundary or outside
// which one: phi1 or phi2
Double_t ddotn, xi, yi;
if (TMath::Abs(point[1]-s1*r) < TMath::Abs(point[1]-s2*r)) {
ddotn = s1*dir[0]-c1*dir[1];
if (ddotn>=0) return 0.0;
ddotn = -s2*dir[0]+c2*dir[1];
if (ddotn<=0) return scone;
sfmin = s2*point[0]-c2*point[1];
if (sfmin<=0) return scone;
sfmin /= ddotn;
if (sfmin >= scone) return scone;
xi = point[0]+sfmin*dir[0];
yi = point[1]+sfmin*dir[1];
if (yi*cm-xi*sm<0) return scone;
return sfmin;
}
ddotn = -s2*dir[0]+c2*dir[1];
if (ddotn>=0) return 0.0;
ddotn = s1*dir[0]-c1*dir[1];
if (ddotn<=0) return scone;
sfmin = -s1*point[0]+c1*point[1];
if (sfmin<=0) return scone;
sfmin /= ddotn;
if (sfmin >= scone) return scone;
xi = point[0]+sfmin*dir[0];
yi = point[1]+sfmin*dir[1];
if (yi*cm-xi*sm>0) return scone;
return sfmin;
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistFromInside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from inside point to surface of the tube segment
if (iact<3 && safe) {
*safe = TGeoConeSeg::SafetyS(point, kTRUE, fDz,fRmin1,fRmax1,fRmin2,fRmax2,fPhi1,fPhi2);
if (iact==0) return TGeoShape::Big();
if ((iact==1) && (*safe>step)) return TGeoShape::Big();
}
Double_t phi1 = fPhi1*TMath::DegToRad();
Double_t phi2 = fPhi2*TMath::DegToRad();
Double_t c1 = TMath::Cos(phi1);
Double_t c2 = TMath::Cos(phi2);
Double_t s1 = TMath::Sin(phi1);
Double_t s2 = TMath::Sin(phi2);
Double_t phim = 0.5*(phi1+phi2);
Double_t cm = TMath::Cos(phim);
Double_t sm = TMath::Sin(phim);
Double_t dfi = 0.5*(phi2-phi1);
Double_t cdfi = TMath::Cos(dfi);
// compute distance to surface
return TGeoConeSeg::DistFromInsideS(point,dir,fDz,fRmin1,fRmax1,fRmin2,fRmax2,c1,s1,c2,s2,cm,sm,cdfi);
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistFromOutsideS(Double_t *point, Double_t *dir, Double_t dz,
Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2,
Double_t c1, Double_t s1, Double_t c2, Double_t s2, Double_t cm, Double_t sm, Double_t cdfi)
{
// compute distance from outside point to surface of arbitrary tube
if (dz<=0) return TGeoShape::Big();
Double_t r2, cpsi;
// check Z planes
Double_t xi, yi, zi;
Double_t b,delta;
zi = dz - TMath::Abs(point[2]);
Double_t rin,rout;
Double_t s = TGeoShape::Big();
Double_t snxt=TGeoShape::Big();
Bool_t in = kFALSE;
Bool_t inz = (zi<0)?kFALSE:kTRUE;
if (!inz) {
if (point[2]*dir[2]>=0) return TGeoShape::Big();
s = -zi/TMath::Abs(dir[2]);
xi = point[0]+s*dir[0];
yi = point[1]+s*dir[1];
r2=xi*xi+yi*yi;
if (dir[2]>0) {
rin = rmin1;
rout = rmax1;
} else {
rin = rmin2;
rout = rmax2;
}
if ((rin*rin<=r2) && (r2<=rout*rout)) {
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) return s;
}
}
Double_t zinv = 1./dz;
Double_t rsq = point[0]*point[0]+point[1]*point[1];
Double_t r = TMath::Sqrt(rsq);
Double_t ro1=0.5*(rmin1+rmin2);
Bool_t hasrmin = (ro1>0)?kTRUE:kFALSE;
Double_t tg1 = 0.0;
Bool_t inrmin = kFALSE;
rin = 0.0;
if (hasrmin) {
tg1=0.5*(rmin2-rmin1)*zinv;
rin = ro1+tg1*point[2];
if (rsq > rin*(rin-TGeoShape::Tolerance())) inrmin=kTRUE;
} else {
inrmin = kTRUE;
}
Double_t ro2=0.5*(rmax1+rmax2);
Double_t tg2=0.5*(rmax2-rmax1)*zinv;
rout = ro2+tg2*point[2];
Bool_t inrmax = kFALSE;
if (rsq < rout*(rout+TGeoShape::Tolerance())) inrmax = kTRUE;
Bool_t inphi = kFALSE;
cpsi=point[0]*cm+point[1]*sm;
if (cpsi>r*cdfi-TGeoShape::Tolerance()) inphi = kTRUE;
in = inz & inrmin & inrmax & inphi;
// If inside, we are most likely on a boundary within machine precision.
if (in) {
Double_t safphi = (cpsi-r*cdfi)*TMath::Sqrt(1.-cdfi*cdfi);
Double_t safrmin = (hasrmin)?TMath::Abs(r-rin):(TGeoShape::Big());
Double_t safrmax = TMath::Abs(r-rout);
// check if on Z boundaries
if (zi<safrmax && zi<safrmin && zi<safphi) {
if (point[2]*dir[2]<0) return 0.0;
return TGeoShape::Big();
}
// check if on Rmax boundary
if (safrmax<safrmin && safrmax<safphi) {
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg2*dir[2]*r;
if (ddotn<=0) return 0.0;
return TGeoShape::Big();
}
// check if on phi boundary
if (safphi<safrmin) {
// We may cross again a phi of rmin boundary
// check first if we are on phi1 or phi2
Double_t un;
if (TMath::Abs(point[1]-s1*r) < TMath::Abs(point[1]-s2*r)) {
un = dir[0]*s1-dir[1]*c1;
if (un < 0) return 0.0;
if (cdfi>=0) return TGeoShape::Big();
un = -dir[0]*s2+dir[1]*c2;
if (un<0) {
s = -point[0]*s2+point[1]*c2;
if (s>0) {
s /= (-un);
zi = point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi = point[0]+s*dir[0];
yi = point[1]+s*dir[1];
if ((yi*cm-xi*sm)>0) {
r2=xi*xi+yi*yi;
rin = ro1+tg1*zi;
rout = ro2+tg2*zi;
if ((rin*rin<=r2) && (rout*rout>=r2)) return s;
}
}
}
}
} else {
un = -dir[0]*s2+dir[1]*c2;
if (un < 0) return 0.0;
if (cdfi>=0) return TGeoShape::Big();
un = dir[0]*s1-dir[1]*c1;
if (un<0) {
s = point[0]*s1-point[1]*c1;
if (s>0) {
s /= (-un);
zi = point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi = point[0]+s*dir[0];
yi = point[1]+s*dir[1];
if ((yi*cm-xi*sm)<0) {
r2=xi*xi+yi*yi;
rin = ro1+tg1*zi;
rout = ro2+tg2*zi;
if ((rin*rin<=r2) && (rout*rout>=r2)) return s;
}
}
}
}
}
// We may also cross rmin, second solution coming from outside
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg1*dir[2]*r;
if (ddotn>=0) return TGeoShape::Big();
if (cdfi>=0) return TGeoShape::Big();
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta<0) return TGeoShape::Big();
snxt = -b-delta;
if (snxt<0) return TGeoShape::Big();
snxt = -b+delta;
zi = point[2]+snxt*dir[2];
if (TMath::Abs(zi)>dz) return TGeoShape::Big();
xi = point[0]+snxt*dir[0];
yi = point[1]+snxt*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) return snxt;
return TGeoShape::Big();
}
// We are on rmin boundary: we may cross again rmin or a phi facette
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg1*dir[2]*r;
if (ddotn>=0) return 0.0;
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta<0) return 0.0;
snxt = -b+delta;
if (snxt<0) return TGeoShape::Big();
if (TMath::Abs(-b-delta)>snxt) return TGeoShape::Big();
zi = point[2]+snxt*dir[2];
if (TMath::Abs(zi)>dz) return TGeoShape::Big();
// OK, we cross rmin at snxt - check if within phi range
xi = point[0]+snxt*dir[0];
yi = point[1]+snxt*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) return snxt;
// we cross rmin in the phi gap - we may cross a phi facette
if (cdfi>=0) return TGeoShape::Big();
Double_t un=-dir[0]*s1+dir[1]*c1;
if (un > 0) {
s=point[0]*s1-point[1]*c1;
if (s>=0) {
s /= un;
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
if ((yi*cm-xi*sm)<=0) {
r2=xi*xi+yi*yi;
rin = ro1+tg1*zi;
rout = ro2+tg2*zi;
if ((rin*rin<=r2) && (rout*rout>=r2)) return s;
}
}
}
}
un=dir[0]*s2-dir[1]*c2;
if (un > 0) {
s=(point[1]*c2-point[0]*s2)/un;
if (s>=0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
if ((yi*cm-xi*sm)>=0) {
r2=xi*xi+yi*yi;
rin = ro1+tg1*zi;
rout = ro2+tg2*zi;
if ((rin*rin<=r2) && (rout*rout>=r2)) return s;
}
}
}
}
return TGeoShape::Big();
}
// The point is really outside
Double_t sr1 = TGeoShape::Big();
if (!inrmax) {
// check crossing with outer cone
TGeoCone::DistToCone(point, dir, dz, rmax1, rmax2, b, delta);
if (delta>=0) {
s = -b-delta;
if (s>0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) return s; // rmax crossing
}
}
s = -b+delta;
if (s>0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) sr1=s;
}
}
}
}
// check crossing with inner cone
Double_t sr2 = TGeoShape::Big();
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta>=0) {
s = -b-delta;
if (s>0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) sr2=s;
}
}
if (sr2>1E10) {
s = -b+delta;
if (s>0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) sr2=s;
}
}
}
}
snxt = TMath::Min(sr1,sr2);
// Check phi crossing
s = TGeoShape::DistToPhiMin(point,dir,s1,c1,s2,c2,sm,cm,kFALSE);
if (s>snxt) return snxt;
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)>dz) return snxt;
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
rout = ro2+tg2*zi;
if (r2>rout*rout) return snxt;
rin = ro1+tg1*zi;
if (r2>=rin*rin) return s; // phi crossing
return snxt;
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistFromOutside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from outside point to surface of the tube
// compute safe radius
if (iact<3 && safe) {
*safe = Safety(point, kFALSE);
if (iact==0) return TGeoShape::Big();
if ((iact==1) && (*safe>step)) return TGeoShape::Big();
}
Double_t phi1 = fPhi1*TMath::DegToRad();
Double_t phi2 = fPhi2*TMath::DegToRad();
Double_t c1 = TMath::Cos(phi1);
Double_t c2 = TMath::Cos(phi2);
Double_t s1 = TMath::Sin(phi1);
Double_t s2 = TMath::Sin(phi2);
Double_t phim = 0.5*(phi1+phi2);
Double_t cm = TMath::Cos(phim);
Double_t sm = TMath::Sin(phim);
Double_t dfi = 0.5*(phi2-phi1);
Double_t cdfi = TMath::Cos(dfi);
return TGeoConeSeg::DistFromOutsideS(point,dir,fDz,fRmin1,fRmax1,fRmin2,fRmax2,c1,s1,c2,s2,cm,sm,cdfi);
}
//_____________________________________________________________________________
Int_t TGeoConeSeg::DistancetoPrimitive(Int_t px, Int_t py)
{
// compute closest distance from point px,py to each corner
Int_t n = gGeoManager->GetNsegments()+1;
const Int_t numPoints = 4*n;
return ShapeDistancetoPrimitive(numPoints, px, py);
}
//_____________________________________________________________________________
TGeoVolume *TGeoConeSeg::Divide(TGeoVolume *voldiv, const char *divname, Int_t iaxis, Int_t ndiv,
Double_t start, Double_t step)
{
//--- Divide this cone segment shape belonging to volume "voldiv" into ndiv volumes
// called divname, from start position with the given step. Returns pointer
// to created division cell volume in case of Z divisions. For Z division
// creates all volumes with different shapes and returns pointer to volume that
// was divided. In case a wrong division axis is supplied, returns pointer to
// volume that was divided.
TGeoShape *shape; //--- shape to be created
TGeoVolume *vol; //--- division volume to be created
TGeoVolumeMulti *vmulti; //--- generic divided volume
TGeoPatternFinder *finder; //--- finder to be attached
TString opt = ""; //--- option to be attached
Double_t dphi;
Int_t id;
Double_t end = start+ndiv*step;
switch (iaxis) {
case 1: //--- R division
Error("Divide","division of a cone segment on R not implemented");
return 0;
case 2: //--- Phi division
dphi = fPhi2-fPhi1;
if (dphi<0) dphi+=360.;
finder = new TGeoPatternCylPhi(voldiv, ndiv, start, end);
voldiv->SetFinder(finder);
finder->SetDivIndex(voldiv->GetNdaughters());
shape = new TGeoConeSeg(fDz, fRmin1, fRmax1, fRmin2, fRmax2, -step/2, step/2);
vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
vmulti->AddVolume(vol);
opt = "Phi";
for (id=0; id<ndiv; id++) {
voldiv->AddNodeOffset(vol, id, start+id*step+step/2, opt.Data());
((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);
}
return vmulti;
case 3: //--- Z division
finder = new TGeoPatternZ(voldiv, ndiv, start, end);
vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
voldiv->SetFinder(finder);
finder->SetDivIndex(voldiv->GetNdaughters());
for (id=0; id<ndiv; id++) {
Double_t z1 = start+id*step;
Double_t z2 = start+(id+1)*step;
Double_t rmin1n = 0.5*(fRmin1*(fDz-z1)+fRmin2*(fDz+z1))/fDz;
Double_t rmax1n = 0.5*(fRmax1*(fDz-z1)+fRmax2*(fDz+z1))/fDz;
Double_t rmin2n = 0.5*(fRmin1*(fDz-z2)+fRmin2*(fDz+z2))/fDz;
Double_t rmax2n = 0.5*(fRmax1*(fDz-z2)+fRmax2*(fDz+z2))/fDz;
shape = new TGeoConeSeg(step/2, rmin1n, rmax1n, rmin2n, rmax2n, fPhi1, fPhi2);
vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
vmulti->AddVolume(vol);
opt = "Z";
voldiv->AddNodeOffset(vol, id, start+id*step+step/2, opt.Data());
((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);
}
return vmulti;
default:
Error("Divide", "Wrong axis type for division");
return 0;
}
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::GetAxisRange(Int_t iaxis, Double_t &xlo, Double_t &xhi) const
{
// Get range of shape for a given axis.
xlo = 0;
xhi = 0;
Double_t dx = 0;
switch (iaxis) {
case 2:
xlo = fPhi1;
xhi = fPhi2;
dx = xhi-xlo;
return dx;
case 3:
xlo = -fDz;
xhi = fDz;
dx = xhi-xlo;
return dx;
}
return dx;
}
//_____________________________________________________________________________
void TGeoConeSeg::GetBoundingCylinder(Double_t *param) const
{
//--- Fill vector param[4] with the bounding cylinder parameters. The order
// is the following : Rmin, Rmax, Phi1, Phi2
param[0] = TMath::Min(fRmin1, fRmin2); // Rmin
param[0] *= param[0];
param[1] = TMath::Max(fRmax1, fRmax2); // Rmax
param[1] *= param[1];
param[2] = (fPhi1<0)?(fPhi1+360.):fPhi1; // Phi1
param[3] = fPhi2; // Phi2
while (param[3]<param[2]) param[3]+=360.;
}
//_____________________________________________________________________________
TGeoShape *TGeoConeSeg::GetMakeRuntimeShape(TGeoShape *mother, TGeoMatrix * /*mat*/) const
{
// in case shape has some negative parameters, these has to be computed
// in order to fit the mother
if (!TestShapeBit(kGeoRunTimeShape)) return 0;
if (!mother->TestShapeBit(kGeoConeSeg)) {
Error("GetMakeRuntimeShape", "invalid mother");
return 0;
}
Double_t rmin1, rmax1, rmin2, rmax2, dz;
rmin1 = fRmin1;
rmax1 = fRmax1;
rmin2 = fRmin2;
rmax2 = fRmax2;
dz = fDz;
if (fDz<0) dz=((TGeoCone*)mother)->GetDz();
if (fRmin1<0)
rmin1 = ((TGeoCone*)mother)->GetRmin1();
if ((fRmax1<0) || (fRmax1<fRmin1))
rmax1 = ((TGeoCone*)mother)->GetRmax1();
if (fRmin2<0)
rmin2 = ((TGeoCone*)mother)->GetRmin2();
if ((fRmax2<0) || (fRmax2<fRmin2))
rmax2 = ((TGeoCone*)mother)->GetRmax2();
return (new TGeoConeSeg(GetName(), dz, rmin1, rmax1, rmin2, rmax2, fPhi1, fPhi2));
}
//_____________________________________________________________________________
void TGeoConeSeg::InspectShape() const
{
// print shape parameters
printf("*** Shape %s: TGeoConeSeg ***\n", GetName());
printf(" dz = %11.5f\n", fDz);
printf(" Rmin1 = %11.5f\n", fRmin1);
printf(" Rmax1 = %11.5f\n", fRmax1);
printf(" Rmin2 = %11.5f\n", fRmin2);
printf(" Rmax2 = %11.5f\n", fRmax2);
printf(" phi1 = %11.5f\n", fPhi1);
printf(" phi2 = %11.5f\n", fPhi2);
printf(" Bounding box:\n");
TGeoBBox::InspectShape();
}
//_____________________________________________________________________________
TBuffer3D *TGeoConeSeg::MakeBuffer3D() const
{
// Creates a TBuffer3D describing *this* shape.
// Coordinates are in local reference frame.
Int_t n = gGeoManager->GetNsegments()+1;
Int_t nbPnts = 4*n;
Int_t nbSegs = 2*nbPnts;
Int_t nbPols = nbPnts-2;
TBuffer3D* buff = new TBuffer3D(TBuffer3DTypes::kGeneric,
nbPnts, 3*nbPnts,
nbSegs, 3*nbSegs,
nbPols, 6*nbPols);
if (buff)
{
SetPoints(buff->fPnts);
SetSegsAndPols(*buff);
}
return buff;
}
//_____________________________________________________________________________
void TGeoConeSeg::SetSegsAndPols(TBuffer3D &buffer) const
{
// Fill TBuffer3D structure for segments and polygons.
Int_t i, j;
Int_t n = gGeoManager->GetNsegments()+1;
Int_t c = GetBasicColor();
memset(buffer.fSegs, 0, buffer.NbSegs()*3*sizeof(Int_t));
for (i = 0; i < 4; i++) {
for (j = 1; j < n; j++) {
buffer.fSegs[(i*n+j-1)*3 ] = c;
buffer.fSegs[(i*n+j-1)*3+1] = i*n+j-1;
buffer.fSegs[(i*n+j-1)*3+2] = i*n+j;
}
}
for (i = 4; i < 6; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c+1;
buffer.fSegs[(i*n+j)*3+1] = (i-4)*n+j;
buffer.fSegs[(i*n+j)*3+2] = (i-2)*n+j;
}
}
for (i = 6; i < 8; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c;
buffer.fSegs[(i*n+j)*3+1] = 2*(i-6)*n+j;
buffer.fSegs[(i*n+j)*3+2] = (2*(i-6)+1)*n+j;
}
}
Int_t indx = 0;
memset(buffer.fPols, 0, buffer.NbPols()*6*sizeof(Int_t));
i = 0;
for (j = 0; j < n-1; j++) {
buffer.fPols[indx++] = c;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = (4+i)*n+j+1;
buffer.fPols[indx++] = (2+i)*n+j;
buffer.fPols[indx++] = (4+i)*n+j;
buffer.fPols[indx++] = i*n+j;
}
i = 1;
for (j = 0; j < n-1; j++) {
buffer.fPols[indx++] = c;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = i*n+j;
buffer.fPols[indx++] = (4+i)*n+j;
buffer.fPols[indx++] = (2+i)*n+j;
buffer.fPols[indx++] = (4+i)*n+j+1;
}
i = 2;
for (j = 0; j < n-1; j++) {
buffer.fPols[indx++] = c+i;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = (i-2)*2*n+j;
buffer.fPols[indx++] = (4+i)*n+j;
buffer.fPols[indx++] = ((i-2)*2+1)*n+j;
buffer.fPols[indx++] = (4+i)*n+j+1;
}
i = 3;
for (j = 0; j < n-1; j++) {
buffer.fPols[indx++] = c+i;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = (4+i)*n+j+1;
buffer.fPols[indx++] = ((i-2)*2+1)*n+j;
buffer.fPols[indx++] = (4+i)*n+j;
buffer.fPols[indx++] = (i-2)*2*n+j;
}
buffer.fPols[indx++] = c+2;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = 6*n;
buffer.fPols[indx++] = 4*n;
buffer.fPols[indx++] = 7*n;
buffer.fPols[indx++] = 5*n;
buffer.fPols[indx++] = c+2;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = 6*n-1;
buffer.fPols[indx++] = 8*n-1;
buffer.fPols[indx++] = 5*n-1;
buffer.fPols[indx++] = 7*n-1;
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::Safety(Double_t *point, Bool_t in) const
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
Double_t saf[3];
Double_t ro1 = 0.5*(fRmin1+fRmin2);
Double_t tg1 = 0.5*(fRmin2-fRmin1)/fDz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(fRmax1+fRmax2);
Double_t tg2 = 0.5*(fRmax2-fRmax1)/fDz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
Double_t safe = TGeoShape::Big();
if (in) {
saf[0] = fDz-TMath::Abs(point[2]);
saf[1] = (r-rin)*cr1;
saf[2] = (rout-r)*cr2;
safe = saf[TMath::LocMin(3,saf)];
} else {
saf[0] = TMath::Abs(point[2])-fDz; // positive if inside
saf[1] = (rin-r)*cr1;
saf[2] = (r-rout)*cr2;
safe = saf[TMath::LocMax(3,saf)];
}
Double_t safphi = TGeoShape::SafetyPhi(point, in, fPhi1, fPhi2);
if (in) return TMath::Min(safe, safphi);
return TMath::Max(safe, safphi);
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::SafetyS(Double_t *point, Bool_t in, Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Double_t phi1, Double_t phi2, Int_t skipz)
{
// Static method to compute the closest distance from given point to this shape.
Double_t saf[3];
Double_t ro1 = 0.5*(rmin1+rmin2);
Double_t tg1 = 0.5*(rmin2-rmin1)/dz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(rmax1+rmax2);
Double_t tg2 = 0.5*(rmax2-rmax1)/dz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
Double_t safe = TGeoShape::Big();
switch (skipz) {
case 1: // skip lower Z plane
saf[0] = dz - point[2];
break;
case 2: // skip upper Z plane
saf[0] = dz + point[2];
break;
case 3: // skip both
saf[0] = TGeoShape::Big();
default:
saf[0] = dz-TMath::Abs(point[2]);
}
saf[1] = (r-rin)*cr1;
saf[2] = (rout-r)*cr2;
Double_t safphi = TGeoShape::SafetyPhi(point,in,phi1,phi2);
if (in) {
safe = saf[TMath::LocMin(3,saf)];
return TMath::Min(safe,safphi);
}
for (Int_t i=0; i<3; i++) saf[i]=-saf[i];
safe = saf[TMath::LocMax(3,saf)];
return TMath::Max(safe,safphi);
}
//_____________________________________________________________________________
void TGeoConeSeg::SavePrimitive(ofstream &out, Option_t * /*option*/)
{
// Save a primitive as a C++ statement(s) on output stream "out".
if (TObject::TestBit(kGeoSavePrimitive)) return;
out << " // Shape: " << GetName() << " type: " << ClassName() << endl;
out << " dz = " << fDz << ";" << endl;
out << " rmin1 = " << fRmin1 << ";" << endl;
out << " rmax1 = " << fRmax1 << ";" << endl;
out << " rmin2 = " << fRmin2 << ";" << endl;
out << " rmax2 = " << fRmax2 << ";" << endl;
out << " phi1 = " << fPhi1 << ";" << endl;
out << " phi2 = " << fPhi2 << ";" << endl;
out << " TGeoShape *" << GetPointerName() << " = new TGeoConeSeg(\"" << GetName() << "\", dz,rmin1,rmax1,rmin2,rmax2,phi1,phi2);" << endl;
TObject::SetBit(TGeoShape::kGeoSavePrimitive);
}
//_____________________________________________________________________________
void TGeoConeSeg::SetConsDimensions(Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Double_t phi1, Double_t phi2)
{
fDz = dz;
fRmin1 = rmin1;
fRmax1 = rmax1;
fRmin2 = rmin2;
fRmax2 = rmax2;
fPhi1 = phi1;
if (fPhi1<0) fPhi1+=360.;
fPhi2 = phi2;
while (fPhi2<fPhi1) fPhi2+=360.;
}
//_____________________________________________________________________________
void TGeoConeSeg::SetDimensions(Double_t *param)
{
Double_t dz = param[0];
Double_t rmin1 = param[1];
Double_t rmax1 = param[2];
Double_t rmin2 = param[3];
Double_t rmax2 = param[4];
Double_t phi1 = param[5];
Double_t phi2 = param[6];
SetConsDimensions(dz, rmin1, rmax1,rmin2, rmax2, phi1, phi2);
}
//_____________________________________________________________________________
void TGeoConeSeg::SetPoints(Double_t *points) const
{
// create cone segment mesh points
Int_t j, n;
Float_t dphi,phi,phi1, phi2,dz;
n = gGeoManager->GetNsegments()+1;
dz = fDz;
phi1 = fPhi1;
phi2 = fPhi2;
dphi = (phi2-phi1)/(n-1);
Int_t indx = 0;
if (points) {
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmin1 * TMath::Cos(phi);
points[indx++] = fRmin1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmax1 * TMath::Cos(phi);
points[indx++] = fRmax1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmin2 * TMath::Cos(phi);
points[indx++] = fRmin2 * TMath::Sin(phi);
points[indx++] = dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmax2 * TMath::Cos(phi);
points[indx++] = fRmax2 * TMath::Sin(phi);
points[indx++] = dz;
}
}
}
//_____________________________________________________________________________
void TGeoConeSeg::SetPoints(Float_t *points) const
{
// create cone segment mesh points
Int_t j, n;
Float_t dphi,phi,phi1, phi2,dz;
n = gGeoManager->GetNsegments()+1;
dz = fDz;
phi1 = fPhi1;
phi2 = fPhi2;
dphi = (phi2-phi1)/(n-1);
Int_t indx = 0;
if (points) {
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmin1 * TMath::Cos(phi);
points[indx++] = fRmin1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmax1 * TMath::Cos(phi);
points[indx++] = fRmax1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmin2 * TMath::Cos(phi);
points[indx++] = fRmin2 * TMath::Sin(phi);
points[indx++] = dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmax2 * TMath::Cos(phi);
points[indx++] = fRmax2 * TMath::Sin(phi);
points[indx++] = dz;
}
}
}
//_____________________________________________________________________________
Int_t TGeoConeSeg::GetNmeshVertices() const
{
// Return number of vertices of the mesh representation
Int_t n = gGeoManager->GetNsegments()+1;
Int_t numPoints = n*4;
return numPoints;
}
//_____________________________________________________________________________
void TGeoConeSeg::Sizeof3D() const
{
///// fill size of this 3-D object
/// TVirtualGeoPainter *painter = gGeoManager->GetGeomPainter();
/// if (!painter) return;
///
/// Int_t n = gGeoManager->GetNsegments()+1;
///
/// Int_t numPoints = n*4;
/// Int_t numSegs = n*8;
/// Int_t numPolys = n*4-2;
/// painter->AddSize3D(numPoints, numSegs, numPolys);
}
//_____________________________________________________________________________
const TBuffer3D & TGeoConeSeg::GetBuffer3D(Int_t reqSections, Bool_t localFrame) const
{
static TBuffer3D buffer(TBuffer3DTypes::kGeneric);
TGeoBBox::FillBuffer3D(buffer, reqSections, localFrame);
if (reqSections & TBuffer3D::kRawSizes) {
Int_t n = gGeoManager->GetNsegments()+1;
Int_t nbPnts = 4*n;
Int_t nbSegs = 2*nbPnts;
Int_t nbPols = nbPnts-2;
if (buffer.SetRawSizes(nbPnts, 3*nbPnts, nbSegs, 3*nbSegs, nbPols, 6*nbPols)) {
buffer.SetSectionsValid(TBuffer3D::kRawSizes);
}
}
if ((reqSections & TBuffer3D::kRaw) && buffer.SectionsValid(TBuffer3D::kRawSizes)) {
SetPoints(buffer.fPnts);
if (!buffer.fLocalFrame) {
TransformPoints(buffer.fPnts, buffer.NbPnts());
}
SetSegsAndPols(buffer);
buffer.SetSectionsValid(TBuffer3D::kRaw);
}
return buffer;
}
*/
//
#include "Riostream.h"
#include "TROOT.h"
#include "TGeoManager.h"
#include "TGeoVolume.h"
#include "TVirtualGeoPainter.h"
#include "TGeoCone.h"
#include "TVirtualPad.h"
#include "TBuffer3D.h"
#include "TBuffer3DTypes.h"
ClassImp(TGeoCone)
//_____________________________________________________________________________
TGeoCone::TGeoCone()
{
// Default constructor
SetShapeBit(TGeoShape::kGeoCone);
fDz = 0.0;
fRmin1 = 0.0;
fRmax1 = 0.0;
fRmin2 = 0.0;
fRmax2 = 0.0;
}
//_____________________________________________________________________________
TGeoCone::TGeoCone(Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2)
:TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoCone);
SetConeDimensions(dz, rmin1, rmax1, rmin2, rmax2);
if ((dz<0) || (rmin1<0) || (rmax1<0) || (rmin2<0) || (rmax2<0)) {
SetShapeBit(kGeoRunTimeShape);
}
else ComputeBBox();
}
//_____________________________________________________________________________
TGeoCone::TGeoCone(const char *name, Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2)
:TGeoBBox(name, 0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoCone);
SetConeDimensions(dz, rmin1, rmax1, rmin2, rmax2);
if ((dz<0) || (rmin1<0) || (rmax1<0) || (rmin2<0) || (rmax2<0)) {
SetShapeBit(kGeoRunTimeShape);
}
else ComputeBBox();
}
//_____________________________________________________________________________
TGeoCone::TGeoCone(Double_t *param)
:TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
// param[0] = dz
// param[1] = Rmin1
// param[2] = Rmax1
// param[3] = Rmin2
// param[4] = Rmax2
SetShapeBit(TGeoShape::kGeoCone);
SetDimensions(param);
if ((fDz<0) || (fRmin1<0) || (fRmax1<0) || (fRmin2<0) || (fRmax2<0))
SetShapeBit(kGeoRunTimeShape);
else ComputeBBox();
}
//_____________________________________________________________________________
TGeoCone::~TGeoCone()
{
// destructor
}
//_____________________________________________________________________________
void TGeoCone::ComputeBBox()
{
// compute bounding box of the sphere
TGeoBBox *box = (TGeoBBox*)this;
box->SetBoxDimensions(TMath::Max(fRmax1, fRmax2), TMath::Max(fRmax1, fRmax2), fDz);
memset(fOrigin, 0, 3*sizeof(Double_t));
}
//_____________________________________________________________________________
void TGeoCone::ComputeNormal(Double_t *point, Double_t *dir, Double_t *norm)
{
// Compute normal to closest surface from POINT.
Double_t safr,safe,phi;
memset(norm,0,3*sizeof(Double_t));
phi = TMath::ATan2(point[1],point[0]);
Double_t cphi = TMath::Cos(phi);
Double_t sphi = TMath::Sin(phi);
Double_t ro1 = 0.5*(fRmin1+fRmin2);
Double_t tg1 = 0.5*(fRmin2-fRmin1)/fDz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(fRmax1+fRmax2);
Double_t tg2 = 0.5*(fRmax2-fRmax1)/fDz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
safe = TMath::Abs(fDz-TMath::Abs(point[2]));
norm[2] = 1;
safr = (ro1>0)?(TMath::Abs((r-rin)*cr1)):TGeoShape::Big();
if (safr<safe) {
safe = safr;
norm[0] = cr1*cphi;
norm[1] = cr1*sphi;
norm[2] = -tg1*cr1;
}
safr = TMath::Abs((rout-r)*cr2);
if (safr<safe) {
norm[0] = cr2*cphi;
norm[1] = cr2*sphi;
norm[2] = -tg2*cr2;
}
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
void TGeoCone::ComputeNormalS(Double_t *point, Double_t *dir, Double_t *norm,
Double_t dz, Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2)
{
// Compute normal to closest surface from POINT.
Double_t safe,phi;
memset(norm,0,3*sizeof(Double_t));
phi = TMath::ATan2(point[1],point[0]);
Double_t cphi = TMath::Cos(phi);
Double_t sphi = TMath::Sin(phi);
Double_t ro1 = 0.5*(rmin1+rmin2);
Double_t tg1 = 0.5*(rmin2-rmin1)/dz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(rmax1+rmax2);
Double_t tg2 = 0.5*(rmax2-rmax1)/dz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
safe = (ro1>0)?(TMath::Abs((r-rin)*cr1)):TGeoShape::Big();
norm[0] = cr1*cphi;
norm[1] = cr1*sphi;
norm[2] = -tg1*cr1;
if (TMath::Abs((rout-r)*cr2)<safe) {
norm[0] = cr2*cphi;
norm[1] = cr2*sphi;
norm[2] = -tg2*cr2;
}
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
Bool_t TGeoCone::Contains(Double_t *point) const
{
// test if point is inside this cone
if (TMath::Abs(point[2]) > fDz) return kFALSE;
Double_t r2 = point[0]*point[0]+point[1]*point[1];
Double_t rl = 0.5*(fRmin2*(point[2]+fDz)+fRmin1*(fDz-point[2]))/fDz;
Double_t rh = 0.5*(fRmax2*(point[2]+fDz)+fRmax1*(fDz-point[2]))/fDz;
if ((r2<rl*rl) || (r2>rh*rh)) return kFALSE;
return kTRUE;
}
//_____________________________________________________________________________
Double_t TGeoCone::DistFromInsideS(Double_t *point, Double_t *dir, Double_t dz,
Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2)
{
// Compute distance from inside point to surface of the cone (static)
// Boundary safe algorithm.
if (dz<=0) return TGeoShape::Big();
// compute distance to surface
// Do Z
Double_t sz = TGeoShape::Big();
if (dir[2]) {
sz = (TMath::Sign(dz, dir[2])-point[2])/dir[2];
if (sz<=0) return 0.0;
}
Double_t rsq=point[0]*point[0]+point[1]*point[1];
Double_t zinv = 1./dz;
Double_t rin = 0.5*(rmin1+rmin2+(rmin2-rmin1)*point[2]*zinv);
// Do Rmin
Double_t sr = TGeoShape::Big();
Double_t b,delta,zi;
if (rin>0) {
// Protection in case point is actually outside the cone
if (rsq < rin*(rin+TGeoShape::Tolerance())) {
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]+0.5*(rmin1-rmin2)*dir[2]*zinv*TMath::Sqrt(rsq);
if (ddotn<=0) return 0.0;
} else {
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta>0) {
sr = -b-delta;
if (sr>0) {
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
}
sr = -b+delta;
if (sr>0) {
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
}
}
}
}
// Do Rmax
Double_t rout = 0.5*(rmax1+rmax2+(rmax2-rmax1)*point[2]*zinv);
if (rsq > rout*(rout-TGeoShape::Tolerance())) {
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]+0.5*(rmax1-rmax2)*dir[2]*zinv*TMath::Sqrt(rsq);
if (ddotn>=0) return 0.0;
TGeoCone::DistToCone(point, dir, dz, rmax1, rmax2, b, delta);
if (delta<0) return 0.0;
sr = -b+delta;
if (sr<0) return sz;
if (TMath::Abs(-b-delta)>sr) return sz;
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
return sz;
}
TGeoCone::DistToCone(point, dir, dz, rmax1, rmax2, b, delta);
if (delta>0) {
sr = -b-delta;
if (sr>0) {
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
}
sr = -b+delta;
if (sr>TGeoShape::Tolerance()) {
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
}
}
return sz;
}
//_____________________________________________________________________________
Double_t TGeoCone::DistFromInside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// Compute distance from inside point to surface of the cone
// Boundary safe algorithm.
if (iact<3 && safe) {
*safe = Safety(point, kTRUE);
if (iact==0) return TGeoShape::Big();
if ((iact==1) && (*safe>step)) return TGeoShape::Big();
}
// compute distance to surface
return TGeoCone::DistFromInsideS(point, dir, fDz, fRmin1, fRmax1, fRmin2, fRmax2);
}
//_____________________________________________________________________________
Double_t TGeoCone::DistFromOutsideS(Double_t *point, Double_t *dir, Double_t dz,
Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2)
{
// Compute distance from outside point to surface of the tube
// Boundary safe algorithm.
// compute distance to Z planes
if (dz<=0) return TGeoShape::Big();
Double_t snxt;
Double_t xp, yp, zp;
Bool_t inz = kTRUE;
if (point[2]<=-dz) {
if (dir[2]<=0) return TGeoShape::Big();
snxt = (-dz-point[2])/dir[2];
xp = point[0]+snxt*dir[0];
yp = point[1]+snxt*dir[1];
Double_t r2 = xp*xp+yp*yp;
if ((r2>=rmin1*rmin1) && (r2<=rmax1*rmax1)) return snxt;
inz = kFALSE;
} else {
if (point[2]>=dz) {
if (dir[2]>=0) return TGeoShape::Big();
snxt = (dz-point[2])/dir[2];
xp = point[0]+snxt*dir[0];
yp = point[1]+snxt*dir[1];
Double_t r2 = xp*xp+yp*yp;
if ((r2>=rmin2*rmin2) && (r2<=rmax2*rmax2)) return snxt;
inz = kFALSE;
}
}
Double_t rsq = point[0]*point[0]+point[1]*point[1];
Double_t dzinv = 1./dz;
Double_t ro1=0.5*(rmin1+rmin2);
Bool_t hasrmin = (ro1>0)?kTRUE:kFALSE;
Double_t tg1 = 0.;
Double_t rin = 0.;
Bool_t inrmin = kTRUE; // r>=rmin
if (hasrmin) {
tg1=0.5*(rmin2-rmin1)*dzinv;
rin=ro1+tg1*point[2];
if (rin>0 && rsq<rin*(rin-TGeoShape::Tolerance())) inrmin=kFALSE;
}
Double_t ro2=0.5*(rmax1+rmax2);
Double_t tg2=0.5*(rmax2-rmax1)*dzinv;
Double_t rout=tg2*point[2]+ro2;
Bool_t inrmax = kFALSE;
if (rout>0 && rsq<rout*(rout+TGeoShape::Tolerance())) inrmax=kTRUE;
Bool_t in = inz & inrmin & inrmax;
Double_t b,delta;
// If inside cone, we are most likely on a boundary within machine precision.
if (in) {
Double_t r=TMath::Sqrt(rsq);
Double_t safz = dz-TMath::Abs(point[2]); // positive
Double_t safrmin = (hasrmin)?(r-rin):TGeoShape::Big();
Double_t safrmax = rout - r;
if (safz<=safrmin && safz<=safrmax) {
// on Z boundary
if (point[2]*dir[2]<0) return 0.0;
return TGeoShape::Big();
}
if (safrmax<safrmin) {
// on rmax boundary
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg2*dir[2]*r;
if (ddotn<=0) return 0.0;
return TGeoShape::Big();
}
// on rmin boundary
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg1*dir[2]*r;
if (ddotn>=0) return 0.0;
// we can cross (+) solution of rmin
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta<0) return 0.0;
snxt = -b+delta;
if (snxt<0) return TGeoShape::Big();
if (TMath::Abs(-b-delta)>snxt) return TGeoShape::Big();
zp = point[2]+snxt*dir[2];
if (TMath::Abs(zp)<=dz) return snxt;
return TGeoShape::Big();
}
// compute distance to inner cone
snxt = TGeoShape::Big();
if (!inrmin) {
// ray can cross only inner cone
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta<0) return TGeoShape::Big();
snxt = -b+delta;
if (snxt<=0) return TGeoShape::Big();
zp = point[2]+snxt*dir[2];
if (TMath::Abs(zp)<=dz) return snxt;
snxt = -b-delta;
if (snxt<=0) return TGeoShape::Big();
zp = point[2]+snxt*dir[2];
if (TMath::Abs(zp)<=dz) return snxt;
return TGeoShape::Big();
} else {
if (hasrmin) {
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta>0) {
Double_t din = -b+delta;
if (din>0) {
zp = point[2]+din*dir[2];
if (TMath::Abs(zp)<=dz) snxt = din;
}
}
}
}
if (inrmax) return snxt;
// we can cross only outer cone, both solutions possible
// compute distance to outer cone
TGeoCone::DistToCone(point, dir, dz, rmax1, rmax2, b, delta);
if (delta<0) return snxt;
Double_t dout = -b-delta;
if (dout>0 && dout<snxt) {
zp = point[2]+dout*dir[2];
if (TMath::Abs(zp)<=dz) return dout;
}
dout = -b+delta;
if (dout<=0 || dout>snxt) return snxt;
zp = point[2]+dout*dir[2];
if (TMath::Abs(zp)<=dz) return dout;
return snxt;
}
//_____________________________________________________________________________
Double_t TGeoCone::DistFromOutside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from outside point to surface of the tube
// compute safe radius
if (iact<3 && safe) {
*safe = Safety(point, kFALSE);
if (iact==0) return TGeoShape::Big();
if ((iact==1) && (*safe>step)) return TGeoShape::Big();
}
// compute distance to Z planes
return TGeoCone::DistFromOutsideS(point, dir, fDz, fRmin1, fRmax1, fRmin2, fRmax2);
}
//_____________________________________________________________________________
void TGeoCone::DistToCone(Double_t *point, Double_t *dir, Double_t dz, Double_t r1, Double_t r2,
Double_t &b, Double_t &delta)
{
// Static method to compute distance to a conical surface with :
// - r1, z1 - radius and Z position of lower base
// - r2, z2 - radius and Z position of upper base
delta = -1.;
if (dz<0) return;
Double_t ro0 = 0.5*(r1+r2);
Double_t tz = 0.5*(r2-r1)/dz;
Double_t rsq = point[0]*point[0] + point[1]*point[1];
Double_t rc = ro0 + point[2]*tz;
Double_t a = dir[0]*dir[0] + dir[1]*dir[1] - tz*tz*dir[2]*dir[2];
b = point[0]*dir[0] + point[1]*dir[1] - tz*rc*dir[2];
Double_t c = rsq - rc*rc;
if (a==0) {
if (b==0) return;
b = 0.5*c/b;
return;
}
a = 1./a;
b *= a;
c *= a;
delta = b*b - c;
if (delta>0) {
delta = TMath::Sqrt(delta);
} else {
delta = -1.;
}
}
//_____________________________________________________________________________
Int_t TGeoCone::DistancetoPrimitive(Int_t px, Int_t py)
{
// compute closest distance from point px,py to each corner
Int_t n = gGeoManager->GetNsegments();
const Int_t numPoints = 4*n;
return ShapeDistancetoPrimitive(numPoints, px, py);
}
//_____________________________________________________________________________
TGeoVolume *TGeoCone::Divide(TGeoVolume *voldiv, const char *divname, Int_t iaxis, Int_t ndiv,
Double_t start, Double_t step)
{
//--- Divide this cone shape belonging to volume "voldiv" into ndiv volumes
// called divname, from start position with the given step. Returns pointer
// to created division cell volume in case of Z divisions. For Z division
// creates all volumes with different shapes and returns pointer to volume that
// was divided. In case a wrong division axis is supplied, returns pointer to
// volume that was divided.
TGeoShape *shape; //--- shape to be created
TGeoVolume *vol; //--- division volume to be created
TGeoVolumeMulti *vmulti; //--- generic divided volume
TGeoPatternFinder *finder; //--- finder to be attached
TString opt = ""; //--- option to be attached
Int_t id;
Double_t end = start+ndiv*step;
switch (iaxis) {
case 1: //--- R division
Error("Divide","division of a cone on R not implemented");
return 0;
case 2: // --- Phi division
finder = new TGeoPatternCylPhi(voldiv, ndiv, start, end);
voldiv->SetFinder(finder);
finder->SetDivIndex(voldiv->GetNdaughters());
shape = new TGeoConeSeg(fDz, fRmin1, fRmax1, fRmin2, fRmax2, -step/2, step/2);
vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
vmulti->AddVolume(vol);
opt = "Phi";
for (id=0; id<ndiv; id++) {
voldiv->AddNodeOffset(vol, id, start+id*step+step/2, opt.Data());
((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);
}
return vmulti;
case 3: //--- Z division
vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
finder = new TGeoPatternZ(voldiv, ndiv, start, end);
voldiv->SetFinder(finder);
finder->SetDivIndex(voldiv->GetNdaughters());
for (id=0; id<ndiv; id++) {
Double_t z1 = start+id*step;
Double_t z2 = start+(id+1)*step;
Double_t rmin1n = 0.5*(fRmin1*(fDz-z1)+fRmin2*(fDz+z1))/fDz;
Double_t rmax1n = 0.5*(fRmax1*(fDz-z1)+fRmax2*(fDz+z1))/fDz;
Double_t rmin2n = 0.5*(fRmin1*(fDz-z2)+fRmin2*(fDz+z2))/fDz;
Double_t rmax2n = 0.5*(fRmax1*(fDz-z2)+fRmax2*(fDz+z2))/fDz;
shape = new TGeoCone(0.5*step,rmin1n, rmax1n, rmin2n, rmax2n);
vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
vmulti->AddVolume(vol);
opt = "Z";
voldiv->AddNodeOffset(vol, id, start+id*step+step/2, opt.Data());
((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);
}
return vmulti;
default:
Error("Divide", "Wrong axis type for division");
return 0;
}
}
//_____________________________________________________________________________
const char *TGeoCone::GetAxisName(Int_t iaxis) const
{
// Returns name of axis IAXIS.
switch (iaxis) {
case 1:
return "R";
case 2:
return "PHI";
case 3:
return "Z";
default:
return "undefined";
}
}
//_____________________________________________________________________________
Double_t TGeoCone::GetAxisRange(Int_t iaxis, Double_t &xlo, Double_t &xhi) const
{
// Get range of shape for a given axis.
xlo = 0;
xhi = 0;
Double_t dx = 0;
switch (iaxis) {
case 2:
xlo = 0.;
xhi = 360.;
return 360.;
case 3:
xlo = -fDz;
xhi = fDz;
dx = xhi-xlo;
return dx;
}
return dx;
}
//_____________________________________________________________________________
void TGeoCone::GetBoundingCylinder(Double_t *param) const
{
//--- Fill vector param[4] with the bounding cylinder parameters. The order
// is the following : Rmin, Rmax, Phi1, Phi2, dZ
param[0] = TMath::Min(fRmin1, fRmin2); // Rmin
param[0] *= param[0];
param[1] = TMath::Max(fRmax1, fRmax2); // Rmax
param[1] *= param[1];
param[2] = 0.; // Phi1
param[3] = 360.; // Phi1
}
//_____________________________________________________________________________
TGeoShape *TGeoCone::GetMakeRuntimeShape(TGeoShape *mother, TGeoMatrix * /*mat*/) const
{
// in case shape has some negative parameters, these has to be computed
// in order to fit the mother
if (!TestShapeBit(kGeoRunTimeShape)) return 0;
if (!mother->TestShapeBit(kGeoCone)) {
Error("GetMakeRuntimeShape", "invalid mother");
return 0;
}
Double_t rmin1, rmax1, rmin2, rmax2, dz;
rmin1 = fRmin1;
rmax1 = fRmax1;
rmin2 = fRmin2;
rmax2 = fRmax2;
dz = fDz;
if (fDz<0) dz=((TGeoCone*)mother)->GetDz();
if (fRmin1<0)
rmin1 = ((TGeoCone*)mother)->GetRmin1();
if (fRmax1<0)
rmax1 = ((TGeoCone*)mother)->GetRmax1();
if (fRmin2<0)
rmin2 = ((TGeoCone*)mother)->GetRmin2();
if (fRmax2<0)
rmax2 = ((TGeoCone*)mother)->GetRmax2();
return (new TGeoCone(GetName(), dz, rmin1, rmax1, rmin2, rmax2));
}
//_____________________________________________________________________________
void TGeoCone::InspectShape() const
{
// print shape parameters
printf("*** Shape %s TGeoCone ***\n", GetName());
printf(" dz =: %11.5f\n", fDz);
printf(" Rmin1 = %11.5f\n", fRmin1);
printf(" Rmax1 = %11.5f\n", fRmax1);
printf(" Rmin2 = %11.5f\n", fRmin2);
printf(" Rmax2 = %11.5f\n", fRmax2);
printf(" Bounding box:\n");
TGeoBBox::InspectShape();
}
//_____________________________________________________________________________
TBuffer3D *TGeoCone::MakeBuffer3D() const
{
// Creates a TBuffer3D describing *this* shape.
// Coordinates are in local reference frame.
Int_t n = gGeoManager->GetNsegments();
Int_t nbPnts = 4*n;
Int_t nbSegs = 8*n;
Int_t nbPols = 4*n;
TBuffer3D* buff = new TBuffer3D(TBuffer3DTypes::kGeneric,
nbPnts, 3*nbPnts,
nbSegs, 3*nbSegs,
nbPols, 6*nbPols);
if (buff)
{
SetPoints(buff->fPnts);
SetSegsAndPols(*buff);
}
return buff;
}
//_____________________________________________________________________________
void TGeoCone::SetSegsAndPols(TBuffer3D &buffer) const
{
// Fill TBuffer3D structure for segments and polygons.
Int_t i,j;
Int_t n = gGeoManager->GetNsegments();
Int_t c = GetBasicColor();
for (i = 0; i < 4; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c;
buffer.fSegs[(i*n+j)*3+1] = i*n+j;
buffer.fSegs[(i*n+j)*3+2] = i*n+j+1;
}
buffer.fSegs[(i*n+j-1)*3+2] = i*n;
}
for (i = 4; i < 6; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c+1;
buffer.fSegs[(i*n+j)*3+1] = (i-4)*n+j;
buffer.fSegs[(i*n+j)*3+2] = (i-2)*n+j;
}
}
for (i = 6; i < 8; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c;
buffer.fSegs[(i*n+j)*3+1] = 2*(i-6)*n+j;
buffer.fSegs[(i*n+j)*3+2] = (2*(i-6)+1)*n+j;
}
}
Int_t indx = 0;
i=0;
for (j = 0; j < n; j++) {
indx = 6*(i*n+j);
buffer.fPols[indx ] = c;
buffer.fPols[indx+1] = 4;
buffer.fPols[indx+5] = i*n+j;
buffer.fPols[indx+4] = (4+i)*n+j;
buffer.fPols[indx+3] = (2+i)*n+j;
buffer.fPols[indx+2] = (4+i)*n+j+1;
}
buffer.fPols[indx+2] = (4+i)*n;
i=1;
for (j = 0; j < n; j++) {
indx = 6*(i*n+j);
buffer.fPols[indx ] = c;
buffer.fPols[indx+1] = 4;
buffer.fPols[indx+2] = i*n+j;
buffer.fPols[indx+3] = (4+i)*n+j;
buffer.fPols[indx+4] = (2+i)*n+j;
buffer.fPols[indx+5] = (4+i)*n+j+1;
}
buffer.fPols[indx+5] = (4+i)*n;
i=2;
for (j = 0; j < n; j++) {
indx = 6*(i*n+j);
buffer.fPols[indx ] = c+i;
buffer.fPols[indx+1] = 4;
buffer.fPols[indx+2] = (i-2)*2*n+j;
buffer.fPols[indx+3] = (4+i)*n+j;
buffer.fPols[indx+4] = ((i-2)*2+1)*n+j;
buffer.fPols[indx+5] = (4+i)*n+j+1;
}
buffer.fPols[indx+5] = (4+i)*n;
i=3;
for (j = 0; j < n; j++) {
indx = 6*(i*n+j);
buffer.fPols[indx ] = c+i;
buffer.fPols[indx+1] = 4;
buffer.fPols[indx+5] = (i-2)*2*n+j;
buffer.fPols[indx+4] = (4+i)*n+j;
buffer.fPols[indx+3] = ((i-2)*2+1)*n+j;
buffer.fPols[indx+2] = (4+i)*n+j+1;
}
buffer.fPols[indx+2] = (4+i)*n;
}
//_____________________________________________________________________________
Double_t TGeoCone::Safety(Double_t *point, Bool_t in) const
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
Double_t saf[3];
Double_t ro1 = 0.5*(fRmin1+fRmin2);
Double_t tg1 = 0.5*(fRmin2-fRmin1)/fDz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(fRmax1+fRmax2);
Double_t tg2 = 0.5*(fRmax2-fRmax1)/fDz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
saf[0] = fDz-TMath::Abs(point[2]);
saf[1] = (ro1>0)?((r-rin)*cr1):TGeoShape::Big();
saf[2] = (rout-r)*cr2;
if (in) return saf[TMath::LocMin(3,saf)];
for (Int_t i=0; i<3; i++) saf[i]=-saf[i];
return saf[TMath::LocMax(3,saf)];
}
//_____________________________________________________________________________
Double_t TGeoCone::SafetyS(Double_t *point, Bool_t in, Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Int_t skipz)
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
Double_t saf[3];
Double_t ro1 = 0.5*(rmin1+rmin2);
Double_t tg1 = 0.5*(rmin2-rmin1)/dz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(rmax1+rmax2);
Double_t tg2 = 0.5*(rmax2-rmax1)/dz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
switch (skipz) {
case 1: // skip lower Z plane
saf[0] = dz - point[2];
break;
case 2: // skip upper Z plane
saf[0] = dz + point[2];
break;
case 3: // skip both
saf[0] = TGeoShape::Big();
break;
default:
saf[0] = dz-TMath::Abs(point[2]);
}
saf[1] = (ro1>0)?((r-rin)*cr1):TGeoShape::Big();
saf[2] = (rout-r)*cr2;
if (in) return saf[TMath::LocMin(3,saf)];
for (Int_t i=0; i<3; i++) saf[i]=-saf[i];
return saf[TMath::LocMax(3,saf)];
}
//_____________________________________________________________________________
void TGeoCone::SavePrimitive(ofstream &out, Option_t * /*option*/)
{
// Save a primitive as a C++ statement(s) on output stream "out".
if (TObject::TestBit(kGeoSavePrimitive)) return;
out << " // Shape: " << GetName() << " type: " << ClassName() << endl;
out << " dz = " << fDz << ";" << endl;
out << " rmin1 = " << fRmin1 << ";" << endl;
out << " rmax1 = " << fRmax1 << ";" << endl;
out << " rmin2 = " << fRmin2 << ";" << endl;
out << " rmax2 = " << fRmax2 << ";" << endl;
out << " TGeoShape *" << GetPointerName() << " = new TGeoCone(\"" << GetName() << "\", dz,rmin1,rmax1,rmin2,rmax2);" << endl;
TObject::SetBit(TGeoShape::kGeoSavePrimitive);
}
//_____________________________________________________________________________
void TGeoCone::SetConeDimensions(Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2)
{
if (rmin1>=0) {
if (rmax1>0) {
if (rmin1<=rmax1) {
// normal rmin/rmax
fRmin1 = rmin1;
fRmax1 = rmax1;
} else {
fRmin1 = rmax1;
fRmax1 = rmin1;
Warning("SetConeDimensions", "rmin1>rmax1 Switch rmin1<->rmax1");
SetShapeBit(TGeoShape::kGeoBad);
}
} else {
// run-time
fRmin1 = rmin1;
fRmax1 = rmax1;
}
} else {
// run-time
fRmin1 = rmin1;
fRmax1 = rmax1;
}
if (rmin2>=0) {
if (rmax2>0) {
if (rmin2<=rmax2) {
// normal rmin/rmax
fRmin2 = rmin2;
fRmax2 = rmax2;
} else {
fRmin2 = rmax2;
fRmax2 = rmin2;
Warning("SetConeDimensions", "rmin2>rmax2 Switch rmin2<->rmax2");
SetShapeBit(TGeoShape::kGeoBad);
}
} else {
// run-time
fRmin2 = rmin2;
fRmax2 = rmax2;
}
} else {
// run-time
fRmin2 = rmin2;
fRmax2 = rmax2;
}
fDz = dz;
}
//_____________________________________________________________________________
void TGeoCone::SetDimensions(Double_t *param)
{
Double_t dz = param[0];
Double_t rmin1 = param[1];
Double_t rmax1 = param[2];
Double_t rmin2 = param[3];
Double_t rmax2 = param[4];
SetConeDimensions(dz, rmin1, rmax1, rmin2, rmax2);
}
//_____________________________________________________________________________
void TGeoCone::SetPoints(Double_t *points) const
{
// create cone mesh points
Double_t dz, phi, dphi;
Int_t j, n;
n = gGeoManager->GetNsegments();
dphi = 360./n;
dz = fDz;
Int_t indx = 0;
if (points) {
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmin1 * TMath::Cos(phi);
points[indx++] = fRmin1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmax1 * TMath::Cos(phi);
points[indx++] = fRmax1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmin2 * TMath::Cos(phi);
points[indx++] = fRmin2 * TMath::Sin(phi);
points[indx++] = dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmax2 * TMath::Cos(phi);
points[indx++] = fRmax2 * TMath::Sin(phi);
points[indx++] = dz;
}
}
}
//_____________________________________________________________________________
void TGeoCone::SetPoints(Float_t *points) const
{
// create cone mesh points
Double_t dz, phi, dphi;
Int_t j, n;
n = gGeoManager->GetNsegments();
dphi = 360./n;
dz = fDz;
Int_t indx = 0;
if (points) {
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmin1 * TMath::Cos(phi);
points[indx++] = fRmin1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmax1 * TMath::Cos(phi);
points[indx++] = fRmax1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmin2 * TMath::Cos(phi);
points[indx++] = fRmin2 * TMath::Sin(phi);
points[indx++] = dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmax2 * TMath::Cos(phi);
points[indx++] = fRmax2 * TMath::Sin(phi);
points[indx++] = dz;
}
}
}
//_____________________________________________________________________________
Int_t TGeoCone::GetNmeshVertices() const
{
// Return number of vertices of the mesh representation
Int_t n = gGeoManager->GetNsegments();
Int_t numPoints = n*4;
return numPoints;
}
//_____________________________________________________________________________
void TGeoCone::Sizeof3D() const
{
///// fill size of this 3-D object
/// TVirtualGeoPainter *painter = gGeoManager->GetGeomPainter();
/// if (!painter) return;
/// Int_t n = gGeoManager->GetNsegments();
/// Int_t numPoints = n*4;
/// Int_t numSegs = n*8;
/// Int_t numPolys = n*4;
/// painter->AddSize3D(numPoints, numSegs, numPolys);
}
//_____________________________________________________________________________
const TBuffer3D & TGeoCone::GetBuffer3D(Int_t reqSections, Bool_t localFrame) const
{
static TBuffer3D buffer(TBuffer3DTypes::kGeneric);
TGeoBBox::FillBuffer3D(buffer, reqSections, localFrame);
if (reqSections & TBuffer3D::kRawSizes) {
Int_t n = gGeoManager->GetNsegments();
Int_t nbPnts = 4*n;
Int_t nbSegs = 8*n;
Int_t nbPols = 4*n;
if (buffer.SetRawSizes(nbPnts, 3*nbPnts, nbSegs, 3*nbSegs, nbPols, 6*nbPols)) {
buffer.SetSectionsValid(TBuffer3D::kRawSizes);
}
}
// TODO: Can we push this as common down to TGeoShape?
if ((reqSections & TBuffer3D::kRaw) && buffer.SectionsValid(TBuffer3D::kRawSizes)) {
SetPoints(buffer.fPnts);
if (!buffer.fLocalFrame) {
TransformPoints(buffer.fPnts, buffer.NbPnts());
}
SetSegsAndPols(buffer);
buffer.SetSectionsValid(TBuffer3D::kRaw);
}
return buffer;
}
ClassImp(TGeoConeSeg)
//_____________________________________________________________________________
TGeoConeSeg::TGeoConeSeg()
{
// Default constructor
SetShapeBit(TGeoShape::kGeoConeSeg);
fPhi1 = fPhi2 = 0.0;
}
//_____________________________________________________________________________
TGeoConeSeg::TGeoConeSeg(Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Double_t phi1, Double_t phi2)
:TGeoCone(dz, rmin1, rmax1, rmin2, rmax2)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoConeSeg);
SetConsDimensions(dz, rmin1, rmax1, rmin2, rmax2, phi1, phi2);
ComputeBBox();
}
//_____________________________________________________________________________
TGeoConeSeg::TGeoConeSeg(const char *name, Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Double_t phi1, Double_t phi2)
:TGeoCone(name, dz, rmin1, rmax1, rmin2, rmax2)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoConeSeg);
SetConsDimensions(dz, rmin1, rmax1, rmin2, rmax2, phi1, phi2);
ComputeBBox();
}
//_____________________________________________________________________________
TGeoConeSeg::TGeoConeSeg(Double_t *param)
:TGeoCone(0,0,0,0,0)
{
// Default constructor specifying minimum and maximum radius
// param[0] = dz
// param[1] = Rmin1
// param[2] = Rmax1
// param[3] = Rmin2
// param[4] = Rmax2
// param[5] = phi1
// param[6] = phi2
SetShapeBit(TGeoShape::kGeoConeSeg);
SetDimensions(param);
ComputeBBox();
}
//_____________________________________________________________________________
TGeoConeSeg::~TGeoConeSeg()
{
// destructor
}
//_____________________________________________________________________________
void TGeoConeSeg::ComputeBBox()
{
// compute bounding box of the tube segment
Double_t rmin, rmax;
rmin = TMath::Min(fRmin1, fRmin2);
rmax = TMath::Max(fRmax1, fRmax2);
Double_t xc[4];
Double_t yc[4];
xc[0] = rmax*TMath::Cos(fPhi1*TMath::DegToRad());
yc[0] = rmax*TMath::Sin(fPhi1*TMath::DegToRad());
xc[1] = rmax*TMath::Cos(fPhi2*TMath::DegToRad());
yc[1] = rmax*TMath::Sin(fPhi2*TMath::DegToRad());
xc[2] = rmin*TMath::Cos(fPhi1*TMath::DegToRad());
yc[2] = rmin*TMath::Sin(fPhi1*TMath::DegToRad());
xc[3] = rmin*TMath::Cos(fPhi2*TMath::DegToRad());
yc[3] = rmin*TMath::Sin(fPhi2*TMath::DegToRad());
Double_t xmin = xc[TMath::LocMin(4, &xc[0])];
Double_t xmax = xc[TMath::LocMax(4, &xc[0])];
Double_t ymin = yc[TMath::LocMin(4, &yc[0])];
Double_t ymax = yc[TMath::LocMax(4, &yc[0])];
Double_t dp = fPhi2-fPhi1;
Double_t ddp = -fPhi1;
if (ddp<0) ddp+= 360;
if (ddp<=dp) xmax = rmax;
ddp = 90-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp<=dp) ymax = rmax;
ddp = 180-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp<=dp) xmin = -rmax;
ddp = 270-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp<=dp) ymin = -rmax;
fOrigin[0] = (xmax+xmin)/2;
fOrigin[1] = (ymax+ymin)/2;
fOrigin[2] = 0;
fDX = (xmax-xmin)/2;
fDY = (ymax-ymin)/2;
fDZ = fDz;
}
//_____________________________________________________________________________
void TGeoConeSeg::ComputeNormal(Double_t *point, Double_t *dir, Double_t *norm)
{
// Compute normal to closest surface from POINT.
Double_t saf[3];
Double_t ro1 = 0.5*(fRmin1+fRmin2);
Double_t tg1 = 0.5*(fRmin2-fRmin1)/fDz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(fRmax1+fRmax2);
Double_t tg2 = 0.5*(fRmax2-fRmax1)/fDz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t c1 = TMath::Cos(fPhi1*TMath::DegToRad());
Double_t s1 = TMath::Sin(fPhi1*TMath::DegToRad());
Double_t c2 = TMath::Cos(fPhi2*TMath::DegToRad());
Double_t s2 = TMath::Sin(fPhi2*TMath::DegToRad());
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
saf[0] = TMath::Abs(fDz-TMath::Abs(point[2]));
saf[1] = (ro1>0)?(TMath::Abs((r-rin)*cr1)):TGeoShape::Big();
saf[2] = TMath::Abs((rout-r)*cr2);
Int_t i = TMath::LocMin(3,saf);
if (TGeoShape::IsCloseToPhi(saf[i], point,c1,s1,c2,s2)) {
TGeoShape::NormalPhi(point,dir,norm,c1,s1,c2,s2);
return;
}
if (i==0) {
norm[0] = norm[1] = 0.;
norm[2] = TMath::Sign(1.,dir[2]);
return;
}
Double_t phi = TMath::ATan2(point[1],point[0]);
Double_t cphi = TMath::Cos(phi);
Double_t sphi = TMath::Sin(phi);
if (i==1) {
norm[0] = cr1*cphi;
norm[1] = cr1*sphi;
norm[2] = -tg1*cr1;
} else {
norm[0] = cr2*cphi;
norm[1] = cr2*sphi;
norm[2] = -tg2*cr2;
}
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
void TGeoConeSeg::ComputeNormalS(Double_t *point, Double_t *dir, Double_t *norm,
Double_t dz, Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2,
Double_t c1, Double_t s1, Double_t c2, Double_t s2)
{
// Compute normal to closest surface from POINT.
Double_t saf[2];
Double_t ro1 = 0.5*(rmin1+rmin2);
Double_t tg1 = 0.5*(rmin2-rmin1)/dz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(rmax1+rmax2);
Double_t tg2 = 0.5*(rmax2-rmax1)/dz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
saf[0] = (ro1>0)?(TMath::Abs((r-rin)*cr1)):TGeoShape::Big();
saf[1] = TMath::Abs((rout-r)*cr2);
Int_t i = TMath::LocMin(2,saf);
if (TGeoShape::IsCloseToPhi(saf[i], point,c1,s1,c2,s2)) {
TGeoShape::NormalPhi(point,dir,norm,c1,s1,c2,s2);
return;
}
Double_t phi = TMath::ATan2(point[1],point[0]);
Double_t cphi = TMath::Cos(phi);
Double_t sphi = TMath::Sin(phi);
if (i==0) {
norm[0] = cr1*cphi;
norm[1] = cr1*sphi;
norm[2] = -tg1*cr1;
} else {
norm[0] = cr2*cphi;
norm[1] = cr2*sphi;
norm[2] = -tg2*cr2;
}
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
Bool_t TGeoConeSeg::Contains(Double_t *point) const
{
// test if point is inside this sphere
if (!TGeoCone::Contains(point)) return kFALSE;
Double_t phi = TMath::ATan2(point[1], point[0]) * TMath::RadToDeg();
if (phi < 0 ) phi+=360.;
Double_t dphi = fPhi2 - fPhi1;
Double_t ddp = phi-fPhi1;
if (ddp < 0) ddp+=360.;
// if (ddp > 360) ddp-=360;
if (ddp > dphi) return kFALSE;
return kTRUE;
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistToCons(Double_t *point, Double_t *dir, Double_t r1, Double_t z1, Double_t r2, Double_t z2, Double_t phi1, Double_t phi2)
{
// Static method to compute distance to a conical surface with :
// - r1, z1 - radius and Z position of lower base
// - r2, z2 - radius and Z position of upper base
// - phi1, phi2 - phi limits
Double_t dz = z2-z1;
if (dz<=0) {
return TGeoShape::Big();
}
Double_t dphi = phi2 - phi1;
if (dphi < 0) dphi+=360.;
// printf("phi1=%f phi2=%f dphi=%f\n", phi1, phi2, dphi);
Double_t ro0 = 0.5*(r1+r2);
Double_t fz = (r2-r1)/dz;
Double_t r0sq = point[0]*point[0] + point[1]*point[1];
Double_t rc = ro0 + fz*(point[2]-0.5*(z1+z2));
Double_t a = dir[0]*dir[0] + dir[1]*dir[1] - fz*fz*dir[2]*dir[2];
Double_t b = point[0]*dir[0] + point[1]*dir[1] - fz*rc*dir[2];
Double_t c = r0sq - rc*rc;
if (a==0) return TGeoShape::Big();
a = 1./a;
b *= a;
c *= a;
Double_t delta = b*b - c;
if (delta<0) return TGeoShape::Big();
delta = TMath::Sqrt(delta);
Double_t snxt = -b-delta;
Double_t ptnew[3];
Double_t ddp, phi;
if (snxt>0) {
// check Z range
ptnew[2] = point[2] + snxt*dir[2];
if (((ptnew[2]-z1)*(ptnew[2]-z2)) < 0) {
// check phi range
ptnew[0] = point[0] + snxt*dir[0];
ptnew[1] = point[1] + snxt*dir[1];
phi = TMath::ATan2(ptnew[1], ptnew[0]) * TMath::RadToDeg();
if (phi < 0 ) phi+=360.;
ddp = phi-phi1;
if (ddp < 0) ddp+=360.;
// printf("snxt1=%f phi=%f ddp=%f\n", snxt, phi, ddp);
if (ddp<=dphi) return snxt;
}
}
snxt = -b+delta;
if (snxt>0) {
// check Z range
ptnew[2] = point[2] + snxt*dir[2];
if (((ptnew[2]-z1)*(ptnew[2]-z2)) < 0) {
// check phi range
ptnew[0] = point[0] + snxt*dir[0];
ptnew[1] = point[1] + snxt*dir[1];
phi = TMath::ATan2(ptnew[1], ptnew[0]) * TMath::RadToDeg();
if (phi < 0 ) phi+=360.;
ddp = phi-phi1;
if (ddp < 0) ddp+=360.;
// printf("snxt2=%f phi=%f ddp=%f\n", snxt, phi, ddp);
if (ddp<=dphi) return snxt;
}
}
return TGeoShape::Big();
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistFromInsideS(Double_t *point, Double_t *dir, Double_t dz,
Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2,
Double_t c1, Double_t s1, Double_t c2, Double_t s2, Double_t cm, Double_t sm, Double_t cdfi)
{
// compute distance from inside point to surface of the tube segment
if (dz<=0) return TGeoShape::Big();
// Do Z
Double_t scone = TGeoCone::DistFromInsideS(point,dir,dz,rmin1,rmax1,rmin2,rmax2);
if (scone<=0) return 0.0;
Double_t sfmin = TGeoShape::Big();
Double_t rsq = point[0]*point[0]+point[1]*point[1];
Double_t r = TMath::Sqrt(rsq);
Double_t cpsi=point[0]*cm+point[1]*sm;
if (cpsi>r*cdfi+TGeoShape::Tolerance()) {
sfmin = TGeoShape::DistToPhiMin(point, dir, s1, c1, s2, c2, sm, cm);
return TMath::Min(scone,sfmin);
}
// Point on the phi boundary or outside
// which one: phi1 or phi2
Double_t ddotn, xi, yi;
if (TMath::Abs(point[1]-s1*r) < TMath::Abs(point[1]-s2*r)) {
ddotn = s1*dir[0]-c1*dir[1];
if (ddotn>=0) return 0.0;
ddotn = -s2*dir[0]+c2*dir[1];
if (ddotn<=0) return scone;
sfmin = s2*point[0]-c2*point[1];
if (sfmin<=0) return scone;
sfmin /= ddotn;
if (sfmin >= scone) return scone;
xi = point[0]+sfmin*dir[0];
yi = point[1]+sfmin*dir[1];
if (yi*cm-xi*sm<0) return scone;
return sfmin;
}
ddotn = -s2*dir[0]+c2*dir[1];
if (ddotn>=0) return 0.0;
ddotn = s1*dir[0]-c1*dir[1];
if (ddotn<=0) return scone;
sfmin = -s1*point[0]+c1*point[1];
if (sfmin<=0) return scone;
sfmin /= ddotn;
if (sfmin >= scone) return scone;
xi = point[0]+sfmin*dir[0];
yi = point[1]+sfmin*dir[1];
if (yi*cm-xi*sm>0) return scone;
return sfmin;
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistFromInside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from inside point to surface of the tube segment
if (iact<3 && safe) {
*safe = TGeoConeSeg::SafetyS(point, kTRUE, fDz,fRmin1,fRmax1,fRmin2,fRmax2,fPhi1,fPhi2);
if (iact==0) return TGeoShape::Big();
if ((iact==1) && (*safe>step)) return TGeoShape::Big();
}
Double_t phi1 = fPhi1*TMath::DegToRad();
Double_t phi2 = fPhi2*TMath::DegToRad();
Double_t c1 = TMath::Cos(phi1);
Double_t c2 = TMath::Cos(phi2);
Double_t s1 = TMath::Sin(phi1);
Double_t s2 = TMath::Sin(phi2);
Double_t phim = 0.5*(phi1+phi2);
Double_t cm = TMath::Cos(phim);
Double_t sm = TMath::Sin(phim);
Double_t dfi = 0.5*(phi2-phi1);
Double_t cdfi = TMath::Cos(dfi);
// compute distance to surface
return TGeoConeSeg::DistFromInsideS(point,dir,fDz,fRmin1,fRmax1,fRmin2,fRmax2,c1,s1,c2,s2,cm,sm,cdfi);
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistFromOutsideS(Double_t *point, Double_t *dir, Double_t dz,
Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2,
Double_t c1, Double_t s1, Double_t c2, Double_t s2, Double_t cm, Double_t sm, Double_t cdfi)
{
// compute distance from outside point to surface of arbitrary tube
if (dz<=0) return TGeoShape::Big();
Double_t r2, cpsi;
// check Z planes
Double_t xi, yi, zi;
Double_t b,delta;
zi = dz - TMath::Abs(point[2]);
Double_t rin,rout;
Double_t s = TGeoShape::Big();
Double_t snxt=TGeoShape::Big();
Bool_t in = kFALSE;
Bool_t inz = (zi<0)?kFALSE:kTRUE;
if (!inz) {
if (point[2]*dir[2]>=0) return TGeoShape::Big();
s = -zi/TMath::Abs(dir[2]);
xi = point[0]+s*dir[0];
yi = point[1]+s*dir[1];
r2=xi*xi+yi*yi;
if (dir[2]>0) {
rin = rmin1;
rout = rmax1;
} else {
rin = rmin2;
rout = rmax2;
}
if ((rin*rin<=r2) && (r2<=rout*rout)) {
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) return s;
}
}
Double_t zinv = 1./dz;
Double_t rsq = point[0]*point[0]+point[1]*point[1];
Double_t r = TMath::Sqrt(rsq);
Double_t ro1=0.5*(rmin1+rmin2);
Bool_t hasrmin = (ro1>0)?kTRUE:kFALSE;
Double_t tg1 = 0.0;
Bool_t inrmin = kFALSE;
rin = 0.0;
if (hasrmin) {
tg1=0.5*(rmin2-rmin1)*zinv;
rin = ro1+tg1*point[2];
if (rsq > rin*(rin-TGeoShape::Tolerance())) inrmin=kTRUE;
} else {
inrmin = kTRUE;
}
Double_t ro2=0.5*(rmax1+rmax2);
Double_t tg2=0.5*(rmax2-rmax1)*zinv;
rout = ro2+tg2*point[2];
Bool_t inrmax = kFALSE;
if (rsq < rout*(rout+TGeoShape::Tolerance())) inrmax = kTRUE;
Bool_t inphi = kFALSE;
cpsi=point[0]*cm+point[1]*sm;
if (cpsi>r*cdfi-TGeoShape::Tolerance()) inphi = kTRUE;
in = inz & inrmin & inrmax & inphi;
// If inside, we are most likely on a boundary within machine precision.
if (in) {
Double_t safphi = (cpsi-r*cdfi)*TMath::Sqrt(1.-cdfi*cdfi);
Double_t safrmin = (hasrmin)?TMath::Abs(r-rin):(TGeoShape::Big());
Double_t safrmax = TMath::Abs(r-rout);
// check if on Z boundaries
if (zi<safrmax && zi<safrmin && zi<safphi) {
if (point[2]*dir[2]<0) return 0.0;
return TGeoShape::Big();
}
// check if on Rmax boundary
if (safrmax<safrmin && safrmax<safphi) {
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg2*dir[2]*r;
if (ddotn<=0) return 0.0;
return TGeoShape::Big();
}
// check if on phi boundary
if (safphi<safrmin) {
// We may cross again a phi of rmin boundary
// check first if we are on phi1 or phi2
Double_t un;
if (TMath::Abs(point[1]-s1*r) < TMath::Abs(point[1]-s2*r)) {
un = dir[0]*s1-dir[1]*c1;
if (un < 0) return 0.0;
if (cdfi>=0) return TGeoShape::Big();
un = -dir[0]*s2+dir[1]*c2;
if (un<0) {
s = -point[0]*s2+point[1]*c2;
if (s>0) {
s /= (-un);
zi = point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi = point[0]+s*dir[0];
yi = point[1]+s*dir[1];
if ((yi*cm-xi*sm)>0) {
r2=xi*xi+yi*yi;
rin = ro1+tg1*zi;
rout = ro2+tg2*zi;
if ((rin*rin<=r2) && (rout*rout>=r2)) return s;
}
}
}
}
} else {
un = -dir[0]*s2+dir[1]*c2;
if (un < 0) return 0.0;
if (cdfi>=0) return TGeoShape::Big();
un = dir[0]*s1-dir[1]*c1;
if (un<0) {
s = point[0]*s1-point[1]*c1;
if (s>0) {
s /= (-un);
zi = point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi = point[0]+s*dir[0];
yi = point[1]+s*dir[1];
if ((yi*cm-xi*sm)<0) {
r2=xi*xi+yi*yi;
rin = ro1+tg1*zi;
rout = ro2+tg2*zi;
if ((rin*rin<=r2) && (rout*rout>=r2)) return s;
}
}
}
}
}
// We may also cross rmin, second solution coming from outside
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg1*dir[2]*r;
if (ddotn>=0) return TGeoShape::Big();
if (cdfi>=0) return TGeoShape::Big();
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta<0) return TGeoShape::Big();
snxt = -b-delta;
if (snxt<0) return TGeoShape::Big();
snxt = -b+delta;
zi = point[2]+snxt*dir[2];
if (TMath::Abs(zi)>dz) return TGeoShape::Big();
xi = point[0]+snxt*dir[0];
yi = point[1]+snxt*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) return snxt;
return TGeoShape::Big();
}
// We are on rmin boundary: we may cross again rmin or a phi facette
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg1*dir[2]*r;
if (ddotn>=0) return 0.0;
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta<0) return 0.0;
snxt = -b+delta;
if (snxt<0) return TGeoShape::Big();
if (TMath::Abs(-b-delta)>snxt) return TGeoShape::Big();
zi = point[2]+snxt*dir[2];
if (TMath::Abs(zi)>dz) return TGeoShape::Big();
// OK, we cross rmin at snxt - check if within phi range
xi = point[0]+snxt*dir[0];
yi = point[1]+snxt*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) return snxt;
// we cross rmin in the phi gap - we may cross a phi facette
if (cdfi>=0) return TGeoShape::Big();
Double_t un=-dir[0]*s1+dir[1]*c1;
if (un > 0) {
s=point[0]*s1-point[1]*c1;
if (s>=0) {
s /= un;
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
if ((yi*cm-xi*sm)<=0) {
r2=xi*xi+yi*yi;
rin = ro1+tg1*zi;
rout = ro2+tg2*zi;
if ((rin*rin<=r2) && (rout*rout>=r2)) return s;
}
}
}
}
un=dir[0]*s2-dir[1]*c2;
if (un > 0) {
s=(point[1]*c2-point[0]*s2)/un;
if (s>=0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
if ((yi*cm-xi*sm)>=0) {
r2=xi*xi+yi*yi;
rin = ro1+tg1*zi;
rout = ro2+tg2*zi;
if ((rin*rin<=r2) && (rout*rout>=r2)) return s;
}
}
}
}
return TGeoShape::Big();
}
// The point is really outside
Double_t sr1 = TGeoShape::Big();
if (!inrmax) {
// check crossing with outer cone
TGeoCone::DistToCone(point, dir, dz, rmax1, rmax2, b, delta);
if (delta>=0) {
s = -b-delta;
if (s>0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) return s; // rmax crossing
}
}
s = -b+delta;
if (s>0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) sr1=s;
}
}
}
}
// check crossing with inner cone
Double_t sr2 = TGeoShape::Big();
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta>=0) {
s = -b-delta;
if (s>0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) sr2=s;
}
}
if (sr2>1E10) {
s = -b+delta;
if (s>0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) sr2=s;
}
}
}
}
snxt = TMath::Min(sr1,sr2);
// Check phi crossing
s = TGeoShape::DistToPhiMin(point,dir,s1,c1,s2,c2,sm,cm,kFALSE);
if (s>snxt) return snxt;
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)>dz) return snxt;
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
rout = ro2+tg2*zi;
if (r2>rout*rout) return snxt;
rin = ro1+tg1*zi;
if (r2>=rin*rin) return s; // phi crossing
return snxt;
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistFromOutside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from outside point to surface of the tube
// compute safe radius
if (iact<3 && safe) {
*safe = Safety(point, kFALSE);
if (iact==0) return TGeoShape::Big();
if ((iact==1) && (*safe>step)) return TGeoShape::Big();
}
Double_t phi1 = fPhi1*TMath::DegToRad();
Double_t phi2 = fPhi2*TMath::DegToRad();
Double_t c1 = TMath::Cos(phi1);
Double_t c2 = TMath::Cos(phi2);
Double_t s1 = TMath::Sin(phi1);
Double_t s2 = TMath::Sin(phi2);
Double_t phim = 0.5*(phi1+phi2);
Double_t cm = TMath::Cos(phim);
Double_t sm = TMath::Sin(phim);
Double_t dfi = 0.5*(phi2-phi1);
Double_t cdfi = TMath::Cos(dfi);
return TGeoConeSeg::DistFromOutsideS(point,dir,fDz,fRmin1,fRmax1,fRmin2,fRmax2,c1,s1,c2,s2,cm,sm,cdfi);
}
//_____________________________________________________________________________
Int_t TGeoConeSeg::DistancetoPrimitive(Int_t px, Int_t py)
{
// compute closest distance from point px,py to each corner
Int_t n = gGeoManager->GetNsegments()+1;
const Int_t numPoints = 4*n;
return ShapeDistancetoPrimitive(numPoints, px, py);
}
//_____________________________________________________________________________
TGeoVolume *TGeoConeSeg::Divide(TGeoVolume *voldiv, const char *divname, Int_t iaxis, Int_t ndiv,
Double_t start, Double_t step)
{
//--- Divide this cone segment shape belonging to volume "voldiv" into ndiv volumes
// called divname, from start position with the given step. Returns pointer
// to created division cell volume in case of Z divisions. For Z division
// creates all volumes with different shapes and returns pointer to volume that
// was divided. In case a wrong division axis is supplied, returns pointer to
// volume that was divided.
TGeoShape *shape; //--- shape to be created
TGeoVolume *vol; //--- division volume to be created
TGeoVolumeMulti *vmulti; //--- generic divided volume
TGeoPatternFinder *finder; //--- finder to be attached
TString opt = ""; //--- option to be attached
Double_t dphi;
Int_t id;
Double_t end = start+ndiv*step;
switch (iaxis) {
case 1: //--- R division
Error("Divide","division of a cone segment on R not implemented");
return 0;
case 2: //--- Phi division
dphi = fPhi2-fPhi1;
if (dphi<0) dphi+=360.;
finder = new TGeoPatternCylPhi(voldiv, ndiv, start, end);
voldiv->SetFinder(finder);
finder->SetDivIndex(voldiv->GetNdaughters());
shape = new TGeoConeSeg(fDz, fRmin1, fRmax1, fRmin2, fRmax2, -step/2, step/2);
vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
vmulti->AddVolume(vol);
opt = "Phi";
for (id=0; id<ndiv; id++) {
voldiv->AddNodeOffset(vol, id, start+id*step+step/2, opt.Data());
((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);
}
return vmulti;
case 3: //--- Z division
finder = new TGeoPatternZ(voldiv, ndiv, start, end);
vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
voldiv->SetFinder(finder);
finder->SetDivIndex(voldiv->GetNdaughters());
for (id=0; id<ndiv; id++) {
Double_t z1 = start+id*step;
Double_t z2 = start+(id+1)*step;
Double_t rmin1n = 0.5*(fRmin1*(fDz-z1)+fRmin2*(fDz+z1))/fDz;
Double_t rmax1n = 0.5*(fRmax1*(fDz-z1)+fRmax2*(fDz+z1))/fDz;
Double_t rmin2n = 0.5*(fRmin1*(fDz-z2)+fRmin2*(fDz+z2))/fDz;
Double_t rmax2n = 0.5*(fRmax1*(fDz-z2)+fRmax2*(fDz+z2))/fDz;
shape = new TGeoConeSeg(step/2, rmin1n, rmax1n, rmin2n, rmax2n, fPhi1, fPhi2);
vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
vmulti->AddVolume(vol);
opt = "Z";
voldiv->AddNodeOffset(vol, id, start+id*step+step/2, opt.Data());
((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);
}
return vmulti;
default:
Error("Divide", "Wrong axis type for division");
return 0;
}
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::GetAxisRange(Int_t iaxis, Double_t &xlo, Double_t &xhi) const
{
// Get range of shape for a given axis.
xlo = 0;
xhi = 0;
Double_t dx = 0;
switch (iaxis) {
case 2:
xlo = fPhi1;
xhi = fPhi2;
dx = xhi-xlo;
return dx;
case 3:
xlo = -fDz;
xhi = fDz;
dx = xhi-xlo;
return dx;
}
return dx;
}
//_____________________________________________________________________________
void TGeoConeSeg::GetBoundingCylinder(Double_t *param) const
{
//--- Fill vector param[4] with the bounding cylinder parameters. The order
// is the following : Rmin, Rmax, Phi1, Phi2
param[0] = TMath::Min(fRmin1, fRmin2); // Rmin
param[0] *= param[0];
param[1] = TMath::Max(fRmax1, fRmax2); // Rmax
param[1] *= param[1];
param[2] = (fPhi1<0)?(fPhi1+360.):fPhi1; // Phi1
param[3] = fPhi2; // Phi2
while (param[3]<param[2]) param[3]+=360.;
}
//_____________________________________________________________________________
TGeoShape *TGeoConeSeg::GetMakeRuntimeShape(TGeoShape *mother, TGeoMatrix * /*mat*/) const
{
// in case shape has some negative parameters, these has to be computed
// in order to fit the mother
if (!TestShapeBit(kGeoRunTimeShape)) return 0;
if (!mother->TestShapeBit(kGeoConeSeg)) {
Error("GetMakeRuntimeShape", "invalid mother");
return 0;
}
Double_t rmin1, rmax1, rmin2, rmax2, dz;
rmin1 = fRmin1;
rmax1 = fRmax1;
rmin2 = fRmin2;
rmax2 = fRmax2;
dz = fDz;
if (fDz<0) dz=((TGeoCone*)mother)->GetDz();
if (fRmin1<0)
rmin1 = ((TGeoCone*)mother)->GetRmin1();
if ((fRmax1<0) || (fRmax1<fRmin1))
rmax1 = ((TGeoCone*)mother)->GetRmax1();
if (fRmin2<0)
rmin2 = ((TGeoCone*)mother)->GetRmin2();
if ((fRmax2<0) || (fRmax2<fRmin2))
rmax2 = ((TGeoCone*)mother)->GetRmax2();
return (new TGeoConeSeg(GetName(), dz, rmin1, rmax1, rmin2, rmax2, fPhi1, fPhi2));
}
//_____________________________________________________________________________
void TGeoConeSeg::InspectShape() const
{
// print shape parameters
printf("*** Shape %s: TGeoConeSeg ***\n", GetName());
printf(" dz = %11.5f\n", fDz);
printf(" Rmin1 = %11.5f\n", fRmin1);
printf(" Rmax1 = %11.5f\n", fRmax1);
printf(" Rmin2 = %11.5f\n", fRmin2);
printf(" Rmax2 = %11.5f\n", fRmax2);
printf(" phi1 = %11.5f\n", fPhi1);
printf(" phi2 = %11.5f\n", fPhi2);
printf(" Bounding box:\n");
TGeoBBox::InspectShape();
}
//_____________________________________________________________________________
TBuffer3D *TGeoConeSeg::MakeBuffer3D() const
{
// Creates a TBuffer3D describing *this* shape.
// Coordinates are in local reference frame.
Int_t n = gGeoManager->GetNsegments()+1;
Int_t nbPnts = 4*n;
Int_t nbSegs = 2*nbPnts;
Int_t nbPols = nbPnts-2;
TBuffer3D* buff = new TBuffer3D(TBuffer3DTypes::kGeneric,
nbPnts, 3*nbPnts,
nbSegs, 3*nbSegs,
nbPols, 6*nbPols);
if (buff)
{
SetPoints(buff->fPnts);
SetSegsAndPols(*buff);
}
return buff;
}
//_____________________________________________________________________________
void TGeoConeSeg::SetSegsAndPols(TBuffer3D &buffer) const
{
// Fill TBuffer3D structure for segments and polygons.
Int_t i, j;
Int_t n = gGeoManager->GetNsegments()+1;
Int_t c = GetBasicColor();
memset(buffer.fSegs, 0, buffer.NbSegs()*3*sizeof(Int_t));
for (i = 0; i < 4; i++) {
for (j = 1; j < n; j++) {
buffer.fSegs[(i*n+j-1)*3 ] = c;
buffer.fSegs[(i*n+j-1)*3+1] = i*n+j-1;
buffer.fSegs[(i*n+j-1)*3+2] = i*n+j;
}
}
for (i = 4; i < 6; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c+1;
buffer.fSegs[(i*n+j)*3+1] = (i-4)*n+j;
buffer.fSegs[(i*n+j)*3+2] = (i-2)*n+j;
}
}
for (i = 6; i < 8; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c;
buffer.fSegs[(i*n+j)*3+1] = 2*(i-6)*n+j;
buffer.fSegs[(i*n+j)*3+2] = (2*(i-6)+1)*n+j;
}
}
Int_t indx = 0;
memset(buffer.fPols, 0, buffer.NbPols()*6*sizeof(Int_t));
i = 0;
for (j = 0; j < n-1; j++) {
buffer.fPols[indx++] = c;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = (4+i)*n+j+1;
buffer.fPols[indx++] = (2+i)*n+j;
buffer.fPols[indx++] = (4+i)*n+j;
buffer.fPols[indx++] = i*n+j;
}
i = 1;
for (j = 0; j < n-1; j++) {
buffer.fPols[indx++] = c;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = i*n+j;
buffer.fPols[indx++] = (4+i)*n+j;
buffer.fPols[indx++] = (2+i)*n+j;
buffer.fPols[indx++] = (4+i)*n+j+1;
}
i = 2;
for (j = 0; j < n-1; j++) {
buffer.fPols[indx++] = c+i;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = (i-2)*2*n+j;
buffer.fPols[indx++] = (4+i)*n+j;
buffer.fPols[indx++] = ((i-2)*2+1)*n+j;
buffer.fPols[indx++] = (4+i)*n+j+1;
}
i = 3;
for (j = 0; j < n-1; j++) {
buffer.fPols[indx++] = c+i;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = (4+i)*n+j+1;
buffer.fPols[indx++] = ((i-2)*2+1)*n+j;
buffer.fPols[indx++] = (4+i)*n+j;
buffer.fPols[indx++] = (i-2)*2*n+j;
}
buffer.fPols[indx++] = c+2;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = 6*n;
buffer.fPols[indx++] = 4*n;
buffer.fPols[indx++] = 7*n;
buffer.fPols[indx++] = 5*n;
buffer.fPols[indx++] = c+2;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = 6*n-1;
buffer.fPols[indx++] = 8*n-1;
buffer.fPols[indx++] = 5*n-1;
buffer.fPols[indx++] = 7*n-1;
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::Safety(Double_t *point, Bool_t in) const
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
Double_t saf[3];
Double_t ro1 = 0.5*(fRmin1+fRmin2);
Double_t tg1 = 0.5*(fRmin2-fRmin1)/fDz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(fRmax1+fRmax2);
Double_t tg2 = 0.5*(fRmax2-fRmax1)/fDz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
Double_t safe = TGeoShape::Big();
if (in) {
saf[0] = fDz-TMath::Abs(point[2]);
saf[1] = (r-rin)*cr1;
saf[2] = (rout-r)*cr2;
safe = saf[TMath::LocMin(3,saf)];
} else {
saf[0] = TMath::Abs(point[2])-fDz; // positive if inside
saf[1] = (rin-r)*cr1;
saf[2] = (r-rout)*cr2;
safe = saf[TMath::LocMax(3,saf)];
}
Double_t safphi = TGeoShape::SafetyPhi(point, in, fPhi1, fPhi2);
if (in) return TMath::Min(safe, safphi);
return TMath::Max(safe, safphi);
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::SafetyS(Double_t *point, Bool_t in, Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Double_t phi1, Double_t phi2, Int_t skipz)
{
// Static method to compute the closest distance from given point to this shape.
Double_t saf[3];
Double_t ro1 = 0.5*(rmin1+rmin2);
Double_t tg1 = 0.5*(rmin2-rmin1)/dz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(rmax1+rmax2);
Double_t tg2 = 0.5*(rmax2-rmax1)/dz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
Double_t safe = TGeoShape::Big();
switch (skipz) {
case 1: // skip lower Z plane
saf[0] = dz - point[2];
break;
case 2: // skip upper Z plane
saf[0] = dz + point[2];
break;
case 3: // skip both
saf[0] = TGeoShape::Big();
default:
saf[0] = dz-TMath::Abs(point[2]);
}
saf[1] = (r-rin)*cr1;
saf[2] = (rout-r)*cr2;
Double_t safphi = TGeoShape::SafetyPhi(point,in,phi1,phi2);
if (in) {
safe = saf[TMath::LocMin(3,saf)];
return TMath::Min(safe,safphi);
}
for (Int_t i=0; i<3; i++) saf[i]=-saf[i];
safe = saf[TMath::LocMax(3,saf)];
return TMath::Max(safe,safphi);
}
//_____________________________________________________________________________
void TGeoConeSeg::SavePrimitive(ofstream &out, Option_t * /*option*/)
{
// Save a primitive as a C++ statement(s) on output stream "out".
if (TObject::TestBit(kGeoSavePrimitive)) return;
out << " // Shape: " << GetName() << " type: " << ClassName() << endl;
out << " dz = " << fDz << ";" << endl;
out << " rmin1 = " << fRmin1 << ";" << endl;
out << " rmax1 = " << fRmax1 << ";" << endl;
out << " rmin2 = " << fRmin2 << ";" << endl;
out << " rmax2 = " << fRmax2 << ";" << endl;
out << " phi1 = " << fPhi1 << ";" << endl;
out << " phi2 = " << fPhi2 << ";" << endl;
out << " TGeoShape *" << GetPointerName() << " = new TGeoConeSeg(\"" << GetName() << "\", dz,rmin1,rmax1,rmin2,rmax2,phi1,phi2);" << endl;
TObject::SetBit(TGeoShape::kGeoSavePrimitive);
}
//_____________________________________________________________________________
void TGeoConeSeg::SetConsDimensions(Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Double_t phi1, Double_t phi2)
{
fDz = dz;
fRmin1 = rmin1;
fRmax1 = rmax1;
fRmin2 = rmin2;
fRmax2 = rmax2;
fPhi1 = phi1;
if (fPhi1<0) fPhi1+=360.;
fPhi2 = phi2;
while (fPhi2<fPhi1) fPhi2+=360.;
}
//_____________________________________________________________________________
void TGeoConeSeg::SetDimensions(Double_t *param)
{
Double_t dz = param[0];
Double_t rmin1 = param[1];
Double_t rmax1 = param[2];
Double_t rmin2 = param[3];
Double_t rmax2 = param[4];
Double_t phi1 = param[5];
Double_t phi2 = param[6];
SetConsDimensions(dz, rmin1, rmax1,rmin2, rmax2, phi1, phi2);
}
//_____________________________________________________________________________
void TGeoConeSeg::SetPoints(Double_t *points) const
{
// create cone segment mesh points
Int_t j, n;
Float_t dphi,phi,phi1, phi2,dz;
n = gGeoManager->GetNsegments()+1;
dz = fDz;
phi1 = fPhi1;
phi2 = fPhi2;
dphi = (phi2-phi1)/(n-1);
Int_t indx = 0;
if (points) {
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmin1 * TMath::Cos(phi);
points[indx++] = fRmin1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmax1 * TMath::Cos(phi);
points[indx++] = fRmax1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmin2 * TMath::Cos(phi);
points[indx++] = fRmin2 * TMath::Sin(phi);
points[indx++] = dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmax2 * TMath::Cos(phi);
points[indx++] = fRmax2 * TMath::Sin(phi);
points[indx++] = dz;
}
}
}
//_____________________________________________________________________________
void TGeoConeSeg::SetPoints(Float_t *points) const
{
// create cone segment mesh points
Int_t j, n;
Float_t dphi,phi,phi1, phi2,dz;
n = gGeoManager->GetNsegments()+1;
dz = fDz;
phi1 = fPhi1;
phi2 = fPhi2;
dphi = (phi2-phi1)/(n-1);
Int_t indx = 0;
if (points) {
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmin1 * TMath::Cos(phi);
points[indx++] = fRmin1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmax1 * TMath::Cos(phi);
points[indx++] = fRmax1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmin2 * TMath::Cos(phi);
points[indx++] = fRmin2 * TMath::Sin(phi);
points[indx++] = dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmax2 * TMath::Cos(phi);
points[indx++] = fRmax2 * TMath::Sin(phi);
points[indx++] = dz;
}
}
}
//_____________________________________________________________________________
Int_t TGeoConeSeg::GetNmeshVertices() const
{
// Return number of vertices of the mesh representation
Int_t n = gGeoManager->GetNsegments()+1;
Int_t numPoints = n*4;
return numPoints;
}
//_____________________________________________________________________________
void TGeoConeSeg::Sizeof3D() const
{
///// fill size of this 3-D object
/// TVirtualGeoPainter *painter = gGeoManager->GetGeomPainter();
/// if (!painter) return;
///
/// Int_t n = gGeoManager->GetNsegments()+1;
///
/// Int_t numPoints = n*4;
/// Int_t numSegs = n*8;
/// Int_t numPolys = n*4-2;
/// painter->AddSize3D(numPoints, numSegs, numPolys);
}
//_____________________________________________________________________________
const TBuffer3D & TGeoConeSeg::GetBuffer3D(Int_t reqSections, Bool_t localFrame) const
{
static TBuffer3D buffer(TBuffer3DTypes::kGeneric);
TGeoBBox::FillBuffer3D(buffer, reqSections, localFrame);
if (reqSections & TBuffer3D::kRawSizes) {
Int_t n = gGeoManager->GetNsegments()+1;
Int_t nbPnts = 4*n;
Int_t nbSegs = 2*nbPnts;
Int_t nbPols = nbPnts-2;
if (buffer.SetRawSizes(nbPnts, 3*nbPnts, nbSegs, 3*nbSegs, nbPols, 6*nbPols)) {
buffer.SetSectionsValid(TBuffer3D::kRawSizes);
}
}
if ((reqSections & TBuffer3D::kRaw) && buffer.SectionsValid(TBuffer3D::kRawSizes)) {
SetPoints(buffer.fPnts);
if (!buffer.fLocalFrame) {
TransformPoints(buffer.fPnts, buffer.NbPnts());
}
SetSegsAndPols(buffer);
buffer.SetSectionsValid(TBuffer3D::kRaw);
}
return buffer;
}
ROOT page - Class index - Class Hierarchy - Top of the page
This page has been automatically generated. If you have any comments or suggestions about the page layout send a mail to ROOT support, or contact the developers with any questions or problems regarding ROOT.
 */
//
//
//
/*
*/
//
//
//
/*
 */
//
//
//
/*
*/
//
//
//
/*
 */
//
//
/*
*/
//
//
/*
 */
//
//--------------------------------------------------------------------------
// TGeoConeSeg - a phi segment of a conical tube. Has 7 parameters :
// - the same 5 as a cone;
// - first phi limit (in degrees)
// - second phi limit
//
//--------------------------------------------------------------------------
//
//
/*
*/
//
//--------------------------------------------------------------------------
// TGeoConeSeg - a phi segment of a conical tube. Has 7 parameters :
// - the same 5 as a cone;
// - first phi limit (in degrees)
// - second phi limit
//
//--------------------------------------------------------------------------
//
//
/*
 */
//
//
//
/*
*/
//
//
//
/*
 */
//
#include "Riostream.h"
#include "TROOT.h"
#include "TGeoManager.h"
#include "TGeoVolume.h"
#include "TVirtualGeoPainter.h"
#include "TGeoCone.h"
#include "TVirtualPad.h"
#include "TBuffer3D.h"
#include "TBuffer3DTypes.h"
ClassImp(TGeoCone)
//_____________________________________________________________________________
TGeoCone::TGeoCone()
{
// Default constructor
SetShapeBit(TGeoShape::kGeoCone);
fDz = 0.0;
fRmin1 = 0.0;
fRmax1 = 0.0;
fRmin2 = 0.0;
fRmax2 = 0.0;
}
//_____________________________________________________________________________
TGeoCone::TGeoCone(Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2)
:TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoCone);
SetConeDimensions(dz, rmin1, rmax1, rmin2, rmax2);
if ((dz<0) || (rmin1<0) || (rmax1<0) || (rmin2<0) || (rmax2<0)) {
SetShapeBit(kGeoRunTimeShape);
}
else ComputeBBox();
}
//_____________________________________________________________________________
TGeoCone::TGeoCone(const char *name, Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2)
:TGeoBBox(name, 0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoCone);
SetConeDimensions(dz, rmin1, rmax1, rmin2, rmax2);
if ((dz<0) || (rmin1<0) || (rmax1<0) || (rmin2<0) || (rmax2<0)) {
SetShapeBit(kGeoRunTimeShape);
}
else ComputeBBox();
}
//_____________________________________________________________________________
TGeoCone::TGeoCone(Double_t *param)
:TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
// param[0] = dz
// param[1] = Rmin1
// param[2] = Rmax1
// param[3] = Rmin2
// param[4] = Rmax2
SetShapeBit(TGeoShape::kGeoCone);
SetDimensions(param);
if ((fDz<0) || (fRmin1<0) || (fRmax1<0) || (fRmin2<0) || (fRmax2<0))
SetShapeBit(kGeoRunTimeShape);
else ComputeBBox();
}
//_____________________________________________________________________________
TGeoCone::~TGeoCone()
{
// destructor
}
//_____________________________________________________________________________
void TGeoCone::ComputeBBox()
{
// compute bounding box of the sphere
TGeoBBox *box = (TGeoBBox*)this;
box->SetBoxDimensions(TMath::Max(fRmax1, fRmax2), TMath::Max(fRmax1, fRmax2), fDz);
memset(fOrigin, 0, 3*sizeof(Double_t));
}
//_____________________________________________________________________________
void TGeoCone::ComputeNormal(Double_t *point, Double_t *dir, Double_t *norm)
{
// Compute normal to closest surface from POINT.
Double_t safr,safe,phi;
memset(norm,0,3*sizeof(Double_t));
phi = TMath::ATan2(point[1],point[0]);
Double_t cphi = TMath::Cos(phi);
Double_t sphi = TMath::Sin(phi);
Double_t ro1 = 0.5*(fRmin1+fRmin2);
Double_t tg1 = 0.5*(fRmin2-fRmin1)/fDz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(fRmax1+fRmax2);
Double_t tg2 = 0.5*(fRmax2-fRmax1)/fDz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
safe = TMath::Abs(fDz-TMath::Abs(point[2]));
norm[2] = 1;
safr = (ro1>0)?(TMath::Abs((r-rin)*cr1)):TGeoShape::Big();
if (safr<safe) {
safe = safr;
norm[0] = cr1*cphi;
norm[1] = cr1*sphi;
norm[2] = -tg1*cr1;
}
safr = TMath::Abs((rout-r)*cr2);
if (safr<safe) {
norm[0] = cr2*cphi;
norm[1] = cr2*sphi;
norm[2] = -tg2*cr2;
}
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
void TGeoCone::ComputeNormalS(Double_t *point, Double_t *dir, Double_t *norm,
Double_t dz, Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2)
{
// Compute normal to closest surface from POINT.
Double_t safe,phi;
memset(norm,0,3*sizeof(Double_t));
phi = TMath::ATan2(point[1],point[0]);
Double_t cphi = TMath::Cos(phi);
Double_t sphi = TMath::Sin(phi);
Double_t ro1 = 0.5*(rmin1+rmin2);
Double_t tg1 = 0.5*(rmin2-rmin1)/dz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(rmax1+rmax2);
Double_t tg2 = 0.5*(rmax2-rmax1)/dz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
safe = (ro1>0)?(TMath::Abs((r-rin)*cr1)):TGeoShape::Big();
norm[0] = cr1*cphi;
norm[1] = cr1*sphi;
norm[2] = -tg1*cr1;
if (TMath::Abs((rout-r)*cr2)<safe) {
norm[0] = cr2*cphi;
norm[1] = cr2*sphi;
norm[2] = -tg2*cr2;
}
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
Bool_t TGeoCone::Contains(Double_t *point) const
{
// test if point is inside this cone
if (TMath::Abs(point[2]) > fDz) return kFALSE;
Double_t r2 = point[0]*point[0]+point[1]*point[1];
Double_t rl = 0.5*(fRmin2*(point[2]+fDz)+fRmin1*(fDz-point[2]))/fDz;
Double_t rh = 0.5*(fRmax2*(point[2]+fDz)+fRmax1*(fDz-point[2]))/fDz;
if ((r2<rl*rl) || (r2>rh*rh)) return kFALSE;
return kTRUE;
}
//_____________________________________________________________________________
Double_t TGeoCone::DistFromInsideS(Double_t *point, Double_t *dir, Double_t dz,
Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2)
{
// Compute distance from inside point to surface of the cone (static)
// Boundary safe algorithm.
if (dz<=0) return TGeoShape::Big();
// compute distance to surface
// Do Z
Double_t sz = TGeoShape::Big();
if (dir[2]) {
sz = (TMath::Sign(dz, dir[2])-point[2])/dir[2];
if (sz<=0) return 0.0;
}
Double_t rsq=point[0]*point[0]+point[1]*point[1];
Double_t zinv = 1./dz;
Double_t rin = 0.5*(rmin1+rmin2+(rmin2-rmin1)*point[2]*zinv);
// Do Rmin
Double_t sr = TGeoShape::Big();
Double_t b,delta,zi;
if (rin>0) {
// Protection in case point is actually outside the cone
if (rsq < rin*(rin+TGeoShape::Tolerance())) {
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]+0.5*(rmin1-rmin2)*dir[2]*zinv*TMath::Sqrt(rsq);
if (ddotn<=0) return 0.0;
} else {
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta>0) {
sr = -b-delta;
if (sr>0) {
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
}
sr = -b+delta;
if (sr>0) {
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
}
}
}
}
// Do Rmax
Double_t rout = 0.5*(rmax1+rmax2+(rmax2-rmax1)*point[2]*zinv);
if (rsq > rout*(rout-TGeoShape::Tolerance())) {
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]+0.5*(rmax1-rmax2)*dir[2]*zinv*TMath::Sqrt(rsq);
if (ddotn>=0) return 0.0;
TGeoCone::DistToCone(point, dir, dz, rmax1, rmax2, b, delta);
if (delta<0) return 0.0;
sr = -b+delta;
if (sr<0) return sz;
if (TMath::Abs(-b-delta)>sr) return sz;
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
return sz;
}
TGeoCone::DistToCone(point, dir, dz, rmax1, rmax2, b, delta);
if (delta>0) {
sr = -b-delta;
if (sr>0) {
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
}
sr = -b+delta;
if (sr>TGeoShape::Tolerance()) {
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
}
}
return sz;
}
//_____________________________________________________________________________
Double_t TGeoCone::DistFromInside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// Compute distance from inside point to surface of the cone
// Boundary safe algorithm.
if (iact<3 && safe) {
*safe = Safety(point, kTRUE);
if (iact==0) return TGeoShape::Big();
if ((iact==1) && (*safe>step)) return TGeoShape::Big();
}
// compute distance to surface
return TGeoCone::DistFromInsideS(point, dir, fDz, fRmin1, fRmax1, fRmin2, fRmax2);
}
//_____________________________________________________________________________
Double_t TGeoCone::DistFromOutsideS(Double_t *point, Double_t *dir, Double_t dz,
Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2)
{
// Compute distance from outside point to surface of the tube
// Boundary safe algorithm.
// compute distance to Z planes
if (dz<=0) return TGeoShape::Big();
Double_t snxt;
Double_t xp, yp, zp;
Bool_t inz = kTRUE;
if (point[2]<=-dz) {
if (dir[2]<=0) return TGeoShape::Big();
snxt = (-dz-point[2])/dir[2];
xp = point[0]+snxt*dir[0];
yp = point[1]+snxt*dir[1];
Double_t r2 = xp*xp+yp*yp;
if ((r2>=rmin1*rmin1) && (r2<=rmax1*rmax1)) return snxt;
inz = kFALSE;
} else {
if (point[2]>=dz) {
if (dir[2]>=0) return TGeoShape::Big();
snxt = (dz-point[2])/dir[2];
xp = point[0]+snxt*dir[0];
yp = point[1]+snxt*dir[1];
Double_t r2 = xp*xp+yp*yp;
if ((r2>=rmin2*rmin2) && (r2<=rmax2*rmax2)) return snxt;
inz = kFALSE;
}
}
Double_t rsq = point[0]*point[0]+point[1]*point[1];
Double_t dzinv = 1./dz;
Double_t ro1=0.5*(rmin1+rmin2);
Bool_t hasrmin = (ro1>0)?kTRUE:kFALSE;
Double_t tg1 = 0.;
Double_t rin = 0.;
Bool_t inrmin = kTRUE; // r>=rmin
if (hasrmin) {
tg1=0.5*(rmin2-rmin1)*dzinv;
rin=ro1+tg1*point[2];
if (rin>0 && rsq<rin*(rin-TGeoShape::Tolerance())) inrmin=kFALSE;
}
Double_t ro2=0.5*(rmax1+rmax2);
Double_t tg2=0.5*(rmax2-rmax1)*dzinv;
Double_t rout=tg2*point[2]+ro2;
Bool_t inrmax = kFALSE;
if (rout>0 && rsq<rout*(rout+TGeoShape::Tolerance())) inrmax=kTRUE;
Bool_t in = inz & inrmin & inrmax;
Double_t b,delta;
// If inside cone, we are most likely on a boundary within machine precision.
if (in) {
Double_t r=TMath::Sqrt(rsq);
Double_t safz = dz-TMath::Abs(point[2]); // positive
Double_t safrmin = (hasrmin)?(r-rin):TGeoShape::Big();
Double_t safrmax = rout - r;
if (safz<=safrmin && safz<=safrmax) {
// on Z boundary
if (point[2]*dir[2]<0) return 0.0;
return TGeoShape::Big();
}
if (safrmax<safrmin) {
// on rmax boundary
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg2*dir[2]*r;
if (ddotn<=0) return 0.0;
return TGeoShape::Big();
}
// on rmin boundary
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg1*dir[2]*r;
if (ddotn>=0) return 0.0;
// we can cross (+) solution of rmin
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta<0) return 0.0;
snxt = -b+delta;
if (snxt<0) return TGeoShape::Big();
if (TMath::Abs(-b-delta)>snxt) return TGeoShape::Big();
zp = point[2]+snxt*dir[2];
if (TMath::Abs(zp)<=dz) return snxt;
return TGeoShape::Big();
}
// compute distance to inner cone
snxt = TGeoShape::Big();
if (!inrmin) {
// ray can cross only inner cone
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta<0) return TGeoShape::Big();
snxt = -b+delta;
if (snxt<=0) return TGeoShape::Big();
zp = point[2]+snxt*dir[2];
if (TMath::Abs(zp)<=dz) return snxt;
snxt = -b-delta;
if (snxt<=0) return TGeoShape::Big();
zp = point[2]+snxt*dir[2];
if (TMath::Abs(zp)<=dz) return snxt;
return TGeoShape::Big();
} else {
if (hasrmin) {
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta>0) {
Double_t din = -b+delta;
if (din>0) {
zp = point[2]+din*dir[2];
if (TMath::Abs(zp)<=dz) snxt = din;
}
}
}
}
if (inrmax) return snxt;
// we can cross only outer cone, both solutions possible
// compute distance to outer cone
TGeoCone::DistToCone(point, dir, dz, rmax1, rmax2, b, delta);
if (delta<0) return snxt;
Double_t dout = -b-delta;
if (dout>0 && dout<snxt) {
zp = point[2]+dout*dir[2];
if (TMath::Abs(zp)<=dz) return dout;
}
dout = -b+delta;
if (dout<=0 || dout>snxt) return snxt;
zp = point[2]+dout*dir[2];
if (TMath::Abs(zp)<=dz) return dout;
return snxt;
}
//_____________________________________________________________________________
Double_t TGeoCone::DistFromOutside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from outside point to surface of the tube
// compute safe radius
if (iact<3 && safe) {
*safe = Safety(point, kFALSE);
if (iact==0) return TGeoShape::Big();
if ((iact==1) && (*safe>step)) return TGeoShape::Big();
}
// compute distance to Z planes
return TGeoCone::DistFromOutsideS(point, dir, fDz, fRmin1, fRmax1, fRmin2, fRmax2);
}
//_____________________________________________________________________________
void TGeoCone::DistToCone(Double_t *point, Double_t *dir, Double_t dz, Double_t r1, Double_t r2,
Double_t &b, Double_t &delta)
{
// Static method to compute distance to a conical surface with :
// - r1, z1 - radius and Z position of lower base
// - r2, z2 - radius and Z position of upper base
delta = -1.;
if (dz<0) return;
Double_t ro0 = 0.5*(r1+r2);
Double_t tz = 0.5*(r2-r1)/dz;
Double_t rsq = point[0]*point[0] + point[1]*point[1];
Double_t rc = ro0 + point[2]*tz;
Double_t a = dir[0]*dir[0] + dir[1]*dir[1] - tz*tz*dir[2]*dir[2];
b = point[0]*dir[0] + point[1]*dir[1] - tz*rc*dir[2];
Double_t c = rsq - rc*rc;
if (a==0) {
if (b==0) return;
b = 0.5*c/b;
return;
}
a = 1./a;
b *= a;
c *= a;
delta = b*b - c;
if (delta>0) {
delta = TMath::Sqrt(delta);
} else {
delta = -1.;
}
}
//_____________________________________________________________________________
Int_t TGeoCone::DistancetoPrimitive(Int_t px, Int_t py)
{
// compute closest distance from point px,py to each corner
Int_t n = gGeoManager->GetNsegments();
const Int_t numPoints = 4*n;
return ShapeDistancetoPrimitive(numPoints, px, py);
}
//_____________________________________________________________________________
TGeoVolume *TGeoCone::Divide(TGeoVolume *voldiv, const char *divname, Int_t iaxis, Int_t ndiv,
Double_t start, Double_t step)
{
//--- Divide this cone shape belonging to volume "voldiv" into ndiv volumes
// called divname, from start position with the given step. Returns pointer
// to created division cell volume in case of Z divisions. For Z division
// creates all volumes with different shapes and returns pointer to volume that
// was divided. In case a wrong division axis is supplied, returns pointer to
// volume that was divided.
TGeoShape *shape; //--- shape to be created
TGeoVolume *vol; //--- division volume to be created
TGeoVolumeMulti *vmulti; //--- generic divided volume
TGeoPatternFinder *finder; //--- finder to be attached
TString opt = ""; //--- option to be attached
Int_t id;
Double_t end = start+ndiv*step;
switch (iaxis) {
case 1: //--- R division
Error("Divide","division of a cone on R not implemented");
return 0;
case 2: // --- Phi division
finder = new TGeoPatternCylPhi(voldiv, ndiv, start, end);
voldiv->SetFinder(finder);
finder->SetDivIndex(voldiv->GetNdaughters());
shape = new TGeoConeSeg(fDz, fRmin1, fRmax1, fRmin2, fRmax2, -step/2, step/2);
vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
vmulti->AddVolume(vol);
opt = "Phi";
for (id=0; id<ndiv; id++) {
voldiv->AddNodeOffset(vol, id, start+id*step+step/2, opt.Data());
((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);
}
return vmulti;
case 3: //--- Z division
vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
finder = new TGeoPatternZ(voldiv, ndiv, start, end);
voldiv->SetFinder(finder);
finder->SetDivIndex(voldiv->GetNdaughters());
for (id=0; id<ndiv; id++) {
Double_t z1 = start+id*step;
Double_t z2 = start+(id+1)*step;
Double_t rmin1n = 0.5*(fRmin1*(fDz-z1)+fRmin2*(fDz+z1))/fDz;
Double_t rmax1n = 0.5*(fRmax1*(fDz-z1)+fRmax2*(fDz+z1))/fDz;
Double_t rmin2n = 0.5*(fRmin1*(fDz-z2)+fRmin2*(fDz+z2))/fDz;
Double_t rmax2n = 0.5*(fRmax1*(fDz-z2)+fRmax2*(fDz+z2))/fDz;
shape = new TGeoCone(0.5*step,rmin1n, rmax1n, rmin2n, rmax2n);
vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
vmulti->AddVolume(vol);
opt = "Z";
voldiv->AddNodeOffset(vol, id, start+id*step+step/2, opt.Data());
((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);
}
return vmulti;
default:
Error("Divide", "Wrong axis type for division");
return 0;
}
}
//_____________________________________________________________________________
const char *TGeoCone::GetAxisName(Int_t iaxis) const
{
// Returns name of axis IAXIS.
switch (iaxis) {
case 1:
return "R";
case 2:
return "PHI";
case 3:
return "Z";
default:
return "undefined";
}
}
//_____________________________________________________________________________
Double_t TGeoCone::GetAxisRange(Int_t iaxis, Double_t &xlo, Double_t &xhi) const
{
// Get range of shape for a given axis.
xlo = 0;
xhi = 0;
Double_t dx = 0;
switch (iaxis) {
case 2:
xlo = 0.;
xhi = 360.;
return 360.;
case 3:
xlo = -fDz;
xhi = fDz;
dx = xhi-xlo;
return dx;
}
return dx;
}
//_____________________________________________________________________________
void TGeoCone::GetBoundingCylinder(Double_t *param) const
{
//--- Fill vector param[4] with the bounding cylinder parameters. The order
// is the following : Rmin, Rmax, Phi1, Phi2, dZ
param[0] = TMath::Min(fRmin1, fRmin2); // Rmin
param[0] *= param[0];
param[1] = TMath::Max(fRmax1, fRmax2); // Rmax
param[1] *= param[1];
param[2] = 0.; // Phi1
param[3] = 360.; // Phi1
}
//_____________________________________________________________________________
TGeoShape *TGeoCone::GetMakeRuntimeShape(TGeoShape *mother, TGeoMatrix * /*mat*/) const
{
// in case shape has some negative parameters, these has to be computed
// in order to fit the mother
if (!TestShapeBit(kGeoRunTimeShape)) return 0;
if (!mother->TestShapeBit(kGeoCone)) {
Error("GetMakeRuntimeShape", "invalid mother");
return 0;
}
Double_t rmin1, rmax1, rmin2, rmax2, dz;
rmin1 = fRmin1;
rmax1 = fRmax1;
rmin2 = fRmin2;
rmax2 = fRmax2;
dz = fDz;
if (fDz<0) dz=((TGeoCone*)mother)->GetDz();
if (fRmin1<0)
rmin1 = ((TGeoCone*)mother)->GetRmin1();
if (fRmax1<0)
rmax1 = ((TGeoCone*)mother)->GetRmax1();
if (fRmin2<0)
rmin2 = ((TGeoCone*)mother)->GetRmin2();
if (fRmax2<0)
rmax2 = ((TGeoCone*)mother)->GetRmax2();
return (new TGeoCone(GetName(), dz, rmin1, rmax1, rmin2, rmax2));
}
//_____________________________________________________________________________
void TGeoCone::InspectShape() const
{
// print shape parameters
printf("*** Shape %s TGeoCone ***\n", GetName());
printf(" dz =: %11.5f\n", fDz);
printf(" Rmin1 = %11.5f\n", fRmin1);
printf(" Rmax1 = %11.5f\n", fRmax1);
printf(" Rmin2 = %11.5f\n", fRmin2);
printf(" Rmax2 = %11.5f\n", fRmax2);
printf(" Bounding box:\n");
TGeoBBox::InspectShape();
}
//_____________________________________________________________________________
TBuffer3D *TGeoCone::MakeBuffer3D() const
{
// Creates a TBuffer3D describing *this* shape.
// Coordinates are in local reference frame.
Int_t n = gGeoManager->GetNsegments();
Int_t nbPnts = 4*n;
Int_t nbSegs = 8*n;
Int_t nbPols = 4*n;
TBuffer3D* buff = new TBuffer3D(TBuffer3DTypes::kGeneric,
nbPnts, 3*nbPnts,
nbSegs, 3*nbSegs,
nbPols, 6*nbPols);
if (buff)
{
SetPoints(buff->fPnts);
SetSegsAndPols(*buff);
}
return buff;
}
//_____________________________________________________________________________
void TGeoCone::SetSegsAndPols(TBuffer3D &buffer) const
{
// Fill TBuffer3D structure for segments and polygons.
Int_t i,j;
Int_t n = gGeoManager->GetNsegments();
Int_t c = GetBasicColor();
for (i = 0; i < 4; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c;
buffer.fSegs[(i*n+j)*3+1] = i*n+j;
buffer.fSegs[(i*n+j)*3+2] = i*n+j+1;
}
buffer.fSegs[(i*n+j-1)*3+2] = i*n;
}
for (i = 4; i < 6; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c+1;
buffer.fSegs[(i*n+j)*3+1] = (i-4)*n+j;
buffer.fSegs[(i*n+j)*3+2] = (i-2)*n+j;
}
}
for (i = 6; i < 8; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c;
buffer.fSegs[(i*n+j)*3+1] = 2*(i-6)*n+j;
buffer.fSegs[(i*n+j)*3+2] = (2*(i-6)+1)*n+j;
}
}
Int_t indx = 0;
i=0;
for (j = 0; j < n; j++) {
indx = 6*(i*n+j);
buffer.fPols[indx ] = c;
buffer.fPols[indx+1] = 4;
buffer.fPols[indx+5] = i*n+j;
buffer.fPols[indx+4] = (4+i)*n+j;
buffer.fPols[indx+3] = (2+i)*n+j;
buffer.fPols[indx+2] = (4+i)*n+j+1;
}
buffer.fPols[indx+2] = (4+i)*n;
i=1;
for (j = 0; j < n; j++) {
indx = 6*(i*n+j);
buffer.fPols[indx ] = c;
buffer.fPols[indx+1] = 4;
buffer.fPols[indx+2] = i*n+j;
buffer.fPols[indx+3] = (4+i)*n+j;
buffer.fPols[indx+4] = (2+i)*n+j;
buffer.fPols[indx+5] = (4+i)*n+j+1;
}
buffer.fPols[indx+5] = (4+i)*n;
i=2;
for (j = 0; j < n; j++) {
indx = 6*(i*n+j);
buffer.fPols[indx ] = c+i;
buffer.fPols[indx+1] = 4;
buffer.fPols[indx+2] = (i-2)*2*n+j;
buffer.fPols[indx+3] = (4+i)*n+j;
buffer.fPols[indx+4] = ((i-2)*2+1)*n+j;
buffer.fPols[indx+5] = (4+i)*n+j+1;
}
buffer.fPols[indx+5] = (4+i)*n;
i=3;
for (j = 0; j < n; j++) {
indx = 6*(i*n+j);
buffer.fPols[indx ] = c+i;
buffer.fPols[indx+1] = 4;
buffer.fPols[indx+5] = (i-2)*2*n+j;
buffer.fPols[indx+4] = (4+i)*n+j;
buffer.fPols[indx+3] = ((i-2)*2+1)*n+j;
buffer.fPols[indx+2] = (4+i)*n+j+1;
}
buffer.fPols[indx+2] = (4+i)*n;
}
//_____________________________________________________________________________
Double_t TGeoCone::Safety(Double_t *point, Bool_t in) const
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
Double_t saf[3];
Double_t ro1 = 0.5*(fRmin1+fRmin2);
Double_t tg1 = 0.5*(fRmin2-fRmin1)/fDz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(fRmax1+fRmax2);
Double_t tg2 = 0.5*(fRmax2-fRmax1)/fDz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
saf[0] = fDz-TMath::Abs(point[2]);
saf[1] = (ro1>0)?((r-rin)*cr1):TGeoShape::Big();
saf[2] = (rout-r)*cr2;
if (in) return saf[TMath::LocMin(3,saf)];
for (Int_t i=0; i<3; i++) saf[i]=-saf[i];
return saf[TMath::LocMax(3,saf)];
}
//_____________________________________________________________________________
Double_t TGeoCone::SafetyS(Double_t *point, Bool_t in, Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Int_t skipz)
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
Double_t saf[3];
Double_t ro1 = 0.5*(rmin1+rmin2);
Double_t tg1 = 0.5*(rmin2-rmin1)/dz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(rmax1+rmax2);
Double_t tg2 = 0.5*(rmax2-rmax1)/dz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
switch (skipz) {
case 1: // skip lower Z plane
saf[0] = dz - point[2];
break;
case 2: // skip upper Z plane
saf[0] = dz + point[2];
break;
case 3: // skip both
saf[0] = TGeoShape::Big();
break;
default:
saf[0] = dz-TMath::Abs(point[2]);
}
saf[1] = (ro1>0)?((r-rin)*cr1):TGeoShape::Big();
saf[2] = (rout-r)*cr2;
if (in) return saf[TMath::LocMin(3,saf)];
for (Int_t i=0; i<3; i++) saf[i]=-saf[i];
return saf[TMath::LocMax(3,saf)];
}
//_____________________________________________________________________________
void TGeoCone::SavePrimitive(ofstream &out, Option_t * /*option*/)
{
// Save a primitive as a C++ statement(s) on output stream "out".
if (TObject::TestBit(kGeoSavePrimitive)) return;
out << " // Shape: " << GetName() << " type: " << ClassName() << endl;
out << " dz = " << fDz << ";" << endl;
out << " rmin1 = " << fRmin1 << ";" << endl;
out << " rmax1 = " << fRmax1 << ";" << endl;
out << " rmin2 = " << fRmin2 << ";" << endl;
out << " rmax2 = " << fRmax2 << ";" << endl;
out << " TGeoShape *" << GetPointerName() << " = new TGeoCone(\"" << GetName() << "\", dz,rmin1,rmax1,rmin2,rmax2);" << endl;
TObject::SetBit(TGeoShape::kGeoSavePrimitive);
}
//_____________________________________________________________________________
void TGeoCone::SetConeDimensions(Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2)
{
if (rmin1>=0) {
if (rmax1>0) {
if (rmin1<=rmax1) {
// normal rmin/rmax
fRmin1 = rmin1;
fRmax1 = rmax1;
} else {
fRmin1 = rmax1;
fRmax1 = rmin1;
Warning("SetConeDimensions", "rmin1>rmax1 Switch rmin1<->rmax1");
SetShapeBit(TGeoShape::kGeoBad);
}
} else {
// run-time
fRmin1 = rmin1;
fRmax1 = rmax1;
}
} else {
// run-time
fRmin1 = rmin1;
fRmax1 = rmax1;
}
if (rmin2>=0) {
if (rmax2>0) {
if (rmin2<=rmax2) {
// normal rmin/rmax
fRmin2 = rmin2;
fRmax2 = rmax2;
} else {
fRmin2 = rmax2;
fRmax2 = rmin2;
Warning("SetConeDimensions", "rmin2>rmax2 Switch rmin2<->rmax2");
SetShapeBit(TGeoShape::kGeoBad);
}
} else {
// run-time
fRmin2 = rmin2;
fRmax2 = rmax2;
}
} else {
// run-time
fRmin2 = rmin2;
fRmax2 = rmax2;
}
fDz = dz;
}
//_____________________________________________________________________________
void TGeoCone::SetDimensions(Double_t *param)
{
Double_t dz = param[0];
Double_t rmin1 = param[1];
Double_t rmax1 = param[2];
Double_t rmin2 = param[3];
Double_t rmax2 = param[4];
SetConeDimensions(dz, rmin1, rmax1, rmin2, rmax2);
}
//_____________________________________________________________________________
void TGeoCone::SetPoints(Double_t *points) const
{
// create cone mesh points
Double_t dz, phi, dphi;
Int_t j, n;
n = gGeoManager->GetNsegments();
dphi = 360./n;
dz = fDz;
Int_t indx = 0;
if (points) {
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmin1 * TMath::Cos(phi);
points[indx++] = fRmin1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmax1 * TMath::Cos(phi);
points[indx++] = fRmax1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmin2 * TMath::Cos(phi);
points[indx++] = fRmin2 * TMath::Sin(phi);
points[indx++] = dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmax2 * TMath::Cos(phi);
points[indx++] = fRmax2 * TMath::Sin(phi);
points[indx++] = dz;
}
}
}
//_____________________________________________________________________________
void TGeoCone::SetPoints(Float_t *points) const
{
// create cone mesh points
Double_t dz, phi, dphi;
Int_t j, n;
n = gGeoManager->GetNsegments();
dphi = 360./n;
dz = fDz;
Int_t indx = 0;
if (points) {
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmin1 * TMath::Cos(phi);
points[indx++] = fRmin1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmax1 * TMath::Cos(phi);
points[indx++] = fRmax1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmin2 * TMath::Cos(phi);
points[indx++] = fRmin2 * TMath::Sin(phi);
points[indx++] = dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmax2 * TMath::Cos(phi);
points[indx++] = fRmax2 * TMath::Sin(phi);
points[indx++] = dz;
}
}
}
//_____________________________________________________________________________
Int_t TGeoCone::GetNmeshVertices() const
{
// Return number of vertices of the mesh representation
Int_t n = gGeoManager->GetNsegments();
Int_t numPoints = n*4;
return numPoints;
}
//_____________________________________________________________________________
void TGeoCone::Sizeof3D() const
{
///// fill size of this 3-D object
/// TVirtualGeoPainter *painter = gGeoManager->GetGeomPainter();
/// if (!painter) return;
/// Int_t n = gGeoManager->GetNsegments();
/// Int_t numPoints = n*4;
/// Int_t numSegs = n*8;
/// Int_t numPolys = n*4;
/// painter->AddSize3D(numPoints, numSegs, numPolys);
}
//_____________________________________________________________________________
const TBuffer3D & TGeoCone::GetBuffer3D(Int_t reqSections, Bool_t localFrame) const
{
static TBuffer3D buffer(TBuffer3DTypes::kGeneric);
TGeoBBox::FillBuffer3D(buffer, reqSections, localFrame);
if (reqSections & TBuffer3D::kRawSizes) {
Int_t n = gGeoManager->GetNsegments();
Int_t nbPnts = 4*n;
Int_t nbSegs = 8*n;
Int_t nbPols = 4*n;
if (buffer.SetRawSizes(nbPnts, 3*nbPnts, nbSegs, 3*nbSegs, nbPols, 6*nbPols)) {
buffer.SetSectionsValid(TBuffer3D::kRawSizes);
}
}
// TODO: Can we push this as common down to TGeoShape?
if ((reqSections & TBuffer3D::kRaw) && buffer.SectionsValid(TBuffer3D::kRawSizes)) {
SetPoints(buffer.fPnts);
if (!buffer.fLocalFrame) {
TransformPoints(buffer.fPnts, buffer.NbPnts());
}
SetSegsAndPols(buffer);
buffer.SetSectionsValid(TBuffer3D::kRaw);
}
return buffer;
}
ClassImp(TGeoConeSeg)
//_____________________________________________________________________________
TGeoConeSeg::TGeoConeSeg()
{
// Default constructor
SetShapeBit(TGeoShape::kGeoConeSeg);
fPhi1 = fPhi2 = 0.0;
}
//_____________________________________________________________________________
TGeoConeSeg::TGeoConeSeg(Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Double_t phi1, Double_t phi2)
:TGeoCone(dz, rmin1, rmax1, rmin2, rmax2)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoConeSeg);
SetConsDimensions(dz, rmin1, rmax1, rmin2, rmax2, phi1, phi2);
ComputeBBox();
}
//_____________________________________________________________________________
TGeoConeSeg::TGeoConeSeg(const char *name, Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Double_t phi1, Double_t phi2)
:TGeoCone(name, dz, rmin1, rmax1, rmin2, rmax2)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoConeSeg);
SetConsDimensions(dz, rmin1, rmax1, rmin2, rmax2, phi1, phi2);
ComputeBBox();
}
//_____________________________________________________________________________
TGeoConeSeg::TGeoConeSeg(Double_t *param)
:TGeoCone(0,0,0,0,0)
{
// Default constructor specifying minimum and maximum radius
// param[0] = dz
// param[1] = Rmin1
// param[2] = Rmax1
// param[3] = Rmin2
// param[4] = Rmax2
// param[5] = phi1
// param[6] = phi2
SetShapeBit(TGeoShape::kGeoConeSeg);
SetDimensions(param);
ComputeBBox();
}
//_____________________________________________________________________________
TGeoConeSeg::~TGeoConeSeg()
{
// destructor
}
//_____________________________________________________________________________
void TGeoConeSeg::ComputeBBox()
{
// compute bounding box of the tube segment
Double_t rmin, rmax;
rmin = TMath::Min(fRmin1, fRmin2);
rmax = TMath::Max(fRmax1, fRmax2);
Double_t xc[4];
Double_t yc[4];
xc[0] = rmax*TMath::Cos(fPhi1*TMath::DegToRad());
yc[0] = rmax*TMath::Sin(fPhi1*TMath::DegToRad());
xc[1] = rmax*TMath::Cos(fPhi2*TMath::DegToRad());
yc[1] = rmax*TMath::Sin(fPhi2*TMath::DegToRad());
xc[2] = rmin*TMath::Cos(fPhi1*TMath::DegToRad());
yc[2] = rmin*TMath::Sin(fPhi1*TMath::DegToRad());
xc[3] = rmin*TMath::Cos(fPhi2*TMath::DegToRad());
yc[3] = rmin*TMath::Sin(fPhi2*TMath::DegToRad());
Double_t xmin = xc[TMath::LocMin(4, &xc[0])];
Double_t xmax = xc[TMath::LocMax(4, &xc[0])];
Double_t ymin = yc[TMath::LocMin(4, &yc[0])];
Double_t ymax = yc[TMath::LocMax(4, &yc[0])];
Double_t dp = fPhi2-fPhi1;
Double_t ddp = -fPhi1;
if (ddp<0) ddp+= 360;
if (ddp<=dp) xmax = rmax;
ddp = 90-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp<=dp) ymax = rmax;
ddp = 180-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp<=dp) xmin = -rmax;
ddp = 270-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp<=dp) ymin = -rmax;
fOrigin[0] = (xmax+xmin)/2;
fOrigin[1] = (ymax+ymin)/2;
fOrigin[2] = 0;
fDX = (xmax-xmin)/2;
fDY = (ymax-ymin)/2;
fDZ = fDz;
}
//_____________________________________________________________________________
void TGeoConeSeg::ComputeNormal(Double_t *point, Double_t *dir, Double_t *norm)
{
// Compute normal to closest surface from POINT.
Double_t saf[3];
Double_t ro1 = 0.5*(fRmin1+fRmin2);
Double_t tg1 = 0.5*(fRmin2-fRmin1)/fDz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(fRmax1+fRmax2);
Double_t tg2 = 0.5*(fRmax2-fRmax1)/fDz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t c1 = TMath::Cos(fPhi1*TMath::DegToRad());
Double_t s1 = TMath::Sin(fPhi1*TMath::DegToRad());
Double_t c2 = TMath::Cos(fPhi2*TMath::DegToRad());
Double_t s2 = TMath::Sin(fPhi2*TMath::DegToRad());
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
saf[0] = TMath::Abs(fDz-TMath::Abs(point[2]));
saf[1] = (ro1>0)?(TMath::Abs((r-rin)*cr1)):TGeoShape::Big();
saf[2] = TMath::Abs((rout-r)*cr2);
Int_t i = TMath::LocMin(3,saf);
if (TGeoShape::IsCloseToPhi(saf[i], point,c1,s1,c2,s2)) {
TGeoShape::NormalPhi(point,dir,norm,c1,s1,c2,s2);
return;
}
if (i==0) {
norm[0] = norm[1] = 0.;
norm[2] = TMath::Sign(1.,dir[2]);
return;
}
Double_t phi = TMath::ATan2(point[1],point[0]);
Double_t cphi = TMath::Cos(phi);
Double_t sphi = TMath::Sin(phi);
if (i==1) {
norm[0] = cr1*cphi;
norm[1] = cr1*sphi;
norm[2] = -tg1*cr1;
} else {
norm[0] = cr2*cphi;
norm[1] = cr2*sphi;
norm[2] = -tg2*cr2;
}
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
void TGeoConeSeg::ComputeNormalS(Double_t *point, Double_t *dir, Double_t *norm,
Double_t dz, Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2,
Double_t c1, Double_t s1, Double_t c2, Double_t s2)
{
// Compute normal to closest surface from POINT.
Double_t saf[2];
Double_t ro1 = 0.5*(rmin1+rmin2);
Double_t tg1 = 0.5*(rmin2-rmin1)/dz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(rmax1+rmax2);
Double_t tg2 = 0.5*(rmax2-rmax1)/dz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
saf[0] = (ro1>0)?(TMath::Abs((r-rin)*cr1)):TGeoShape::Big();
saf[1] = TMath::Abs((rout-r)*cr2);
Int_t i = TMath::LocMin(2,saf);
if (TGeoShape::IsCloseToPhi(saf[i], point,c1,s1,c2,s2)) {
TGeoShape::NormalPhi(point,dir,norm,c1,s1,c2,s2);
return;
}
Double_t phi = TMath::ATan2(point[1],point[0]);
Double_t cphi = TMath::Cos(phi);
Double_t sphi = TMath::Sin(phi);
if (i==0) {
norm[0] = cr1*cphi;
norm[1] = cr1*sphi;
norm[2] = -tg1*cr1;
} else {
norm[0] = cr2*cphi;
norm[1] = cr2*sphi;
norm[2] = -tg2*cr2;
}
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
Bool_t TGeoConeSeg::Contains(Double_t *point) const
{
// test if point is inside this sphere
if (!TGeoCone::Contains(point)) return kFALSE;
Double_t phi = TMath::ATan2(point[1], point[0]) * TMath::RadToDeg();
if (phi < 0 ) phi+=360.;
Double_t dphi = fPhi2 - fPhi1;
Double_t ddp = phi-fPhi1;
if (ddp < 0) ddp+=360.;
// if (ddp > 360) ddp-=360;
if (ddp > dphi) return kFALSE;
return kTRUE;
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistToCons(Double_t *point, Double_t *dir, Double_t r1, Double_t z1, Double_t r2, Double_t z2, Double_t phi1, Double_t phi2)
{
// Static method to compute distance to a conical surface with :
// - r1, z1 - radius and Z position of lower base
// - r2, z2 - radius and Z position of upper base
// - phi1, phi2 - phi limits
Double_t dz = z2-z1;
if (dz<=0) {
return TGeoShape::Big();
}
Double_t dphi = phi2 - phi1;
if (dphi < 0) dphi+=360.;
// printf("phi1=%f phi2=%f dphi=%f\n", phi1, phi2, dphi);
Double_t ro0 = 0.5*(r1+r2);
Double_t fz = (r2-r1)/dz;
Double_t r0sq = point[0]*point[0] + point[1]*point[1];
Double_t rc = ro0 + fz*(point[2]-0.5*(z1+z2));
Double_t a = dir[0]*dir[0] + dir[1]*dir[1] - fz*fz*dir[2]*dir[2];
Double_t b = point[0]*dir[0] + point[1]*dir[1] - fz*rc*dir[2];
Double_t c = r0sq - rc*rc;
if (a==0) return TGeoShape::Big();
a = 1./a;
b *= a;
c *= a;
Double_t delta = b*b - c;
if (delta<0) return TGeoShape::Big();
delta = TMath::Sqrt(delta);
Double_t snxt = -b-delta;
Double_t ptnew[3];
Double_t ddp, phi;
if (snxt>0) {
// check Z range
ptnew[2] = point[2] + snxt*dir[2];
if (((ptnew[2]-z1)*(ptnew[2]-z2)) < 0) {
// check phi range
ptnew[0] = point[0] + snxt*dir[0];
ptnew[1] = point[1] + snxt*dir[1];
phi = TMath::ATan2(ptnew[1], ptnew[0]) * TMath::RadToDeg();
if (phi < 0 ) phi+=360.;
ddp = phi-phi1;
if (ddp < 0) ddp+=360.;
// printf("snxt1=%f phi=%f ddp=%f\n", snxt, phi, ddp);
if (ddp<=dphi) return snxt;
}
}
snxt = -b+delta;
if (snxt>0) {
// check Z range
ptnew[2] = point[2] + snxt*dir[2];
if (((ptnew[2]-z1)*(ptnew[2]-z2)) < 0) {
// check phi range
ptnew[0] = point[0] + snxt*dir[0];
ptnew[1] = point[1] + snxt*dir[1];
phi = TMath::ATan2(ptnew[1], ptnew[0]) * TMath::RadToDeg();
if (phi < 0 ) phi+=360.;
ddp = phi-phi1;
if (ddp < 0) ddp+=360.;
// printf("snxt2=%f phi=%f ddp=%f\n", snxt, phi, ddp);
if (ddp<=dphi) return snxt;
}
}
return TGeoShape::Big();
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistFromInsideS(Double_t *point, Double_t *dir, Double_t dz,
Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2,
Double_t c1, Double_t s1, Double_t c2, Double_t s2, Double_t cm, Double_t sm, Double_t cdfi)
{
// compute distance from inside point to surface of the tube segment
if (dz<=0) return TGeoShape::Big();
// Do Z
Double_t scone = TGeoCone::DistFromInsideS(point,dir,dz,rmin1,rmax1,rmin2,rmax2);
if (scone<=0) return 0.0;
Double_t sfmin = TGeoShape::Big();
Double_t rsq = point[0]*point[0]+point[1]*point[1];
Double_t r = TMath::Sqrt(rsq);
Double_t cpsi=point[0]*cm+point[1]*sm;
if (cpsi>r*cdfi+TGeoShape::Tolerance()) {
sfmin = TGeoShape::DistToPhiMin(point, dir, s1, c1, s2, c2, sm, cm);
return TMath::Min(scone,sfmin);
}
// Point on the phi boundary or outside
// which one: phi1 or phi2
Double_t ddotn, xi, yi;
if (TMath::Abs(point[1]-s1*r) < TMath::Abs(point[1]-s2*r)) {
ddotn = s1*dir[0]-c1*dir[1];
if (ddotn>=0) return 0.0;
ddotn = -s2*dir[0]+c2*dir[1];
if (ddotn<=0) return scone;
sfmin = s2*point[0]-c2*point[1];
if (sfmin<=0) return scone;
sfmin /= ddotn;
if (sfmin >= scone) return scone;
xi = point[0]+sfmin*dir[0];
yi = point[1]+sfmin*dir[1];
if (yi*cm-xi*sm<0) return scone;
return sfmin;
}
ddotn = -s2*dir[0]+c2*dir[1];
if (ddotn>=0) return 0.0;
ddotn = s1*dir[0]-c1*dir[1];
if (ddotn<=0) return scone;
sfmin = -s1*point[0]+c1*point[1];
if (sfmin<=0) return scone;
sfmin /= ddotn;
if (sfmin >= scone) return scone;
xi = point[0]+sfmin*dir[0];
yi = point[1]+sfmin*dir[1];
if (yi*cm-xi*sm>0) return scone;
return sfmin;
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistFromInside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from inside point to surface of the tube segment
if (iact<3 && safe) {
*safe = TGeoConeSeg::SafetyS(point, kTRUE, fDz,fRmin1,fRmax1,fRmin2,fRmax2,fPhi1,fPhi2);
if (iact==0) return TGeoShape::Big();
if ((iact==1) && (*safe>step)) return TGeoShape::Big();
}
Double_t phi1 = fPhi1*TMath::DegToRad();
Double_t phi2 = fPhi2*TMath::DegToRad();
Double_t c1 = TMath::Cos(phi1);
Double_t c2 = TMath::Cos(phi2);
Double_t s1 = TMath::Sin(phi1);
Double_t s2 = TMath::Sin(phi2);
Double_t phim = 0.5*(phi1+phi2);
Double_t cm = TMath::Cos(phim);
Double_t sm = TMath::Sin(phim);
Double_t dfi = 0.5*(phi2-phi1);
Double_t cdfi = TMath::Cos(dfi);
// compute distance to surface
return TGeoConeSeg::DistFromInsideS(point,dir,fDz,fRmin1,fRmax1,fRmin2,fRmax2,c1,s1,c2,s2,cm,sm,cdfi);
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistFromOutsideS(Double_t *point, Double_t *dir, Double_t dz,
Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2,
Double_t c1, Double_t s1, Double_t c2, Double_t s2, Double_t cm, Double_t sm, Double_t cdfi)
{
// compute distance from outside point to surface of arbitrary tube
if (dz<=0) return TGeoShape::Big();
Double_t r2, cpsi;
// check Z planes
Double_t xi, yi, zi;
Double_t b,delta;
zi = dz - TMath::Abs(point[2]);
Double_t rin,rout;
Double_t s = TGeoShape::Big();
Double_t snxt=TGeoShape::Big();
Bool_t in = kFALSE;
Bool_t inz = (zi<0)?kFALSE:kTRUE;
if (!inz) {
if (point[2]*dir[2]>=0) return TGeoShape::Big();
s = -zi/TMath::Abs(dir[2]);
xi = point[0]+s*dir[0];
yi = point[1]+s*dir[1];
r2=xi*xi+yi*yi;
if (dir[2]>0) {
rin = rmin1;
rout = rmax1;
} else {
rin = rmin2;
rout = rmax2;
}
if ((rin*rin<=r2) && (r2<=rout*rout)) {
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) return s;
}
}
Double_t zinv = 1./dz;
Double_t rsq = point[0]*point[0]+point[1]*point[1];
Double_t r = TMath::Sqrt(rsq);
Double_t ro1=0.5*(rmin1+rmin2);
Bool_t hasrmin = (ro1>0)?kTRUE:kFALSE;
Double_t tg1 = 0.0;
Bool_t inrmin = kFALSE;
rin = 0.0;
if (hasrmin) {
tg1=0.5*(rmin2-rmin1)*zinv;
rin = ro1+tg1*point[2];
if (rsq > rin*(rin-TGeoShape::Tolerance())) inrmin=kTRUE;
} else {
inrmin = kTRUE;
}
Double_t ro2=0.5*(rmax1+rmax2);
Double_t tg2=0.5*(rmax2-rmax1)*zinv;
rout = ro2+tg2*point[2];
Bool_t inrmax = kFALSE;
if (rsq < rout*(rout+TGeoShape::Tolerance())) inrmax = kTRUE;
Bool_t inphi = kFALSE;
cpsi=point[0]*cm+point[1]*sm;
if (cpsi>r*cdfi-TGeoShape::Tolerance()) inphi = kTRUE;
in = inz & inrmin & inrmax & inphi;
// If inside, we are most likely on a boundary within machine precision.
if (in) {
Double_t safphi = (cpsi-r*cdfi)*TMath::Sqrt(1.-cdfi*cdfi);
Double_t safrmin = (hasrmin)?TMath::Abs(r-rin):(TGeoShape::Big());
Double_t safrmax = TMath::Abs(r-rout);
// check if on Z boundaries
if (zi<safrmax && zi<safrmin && zi<safphi) {
if (point[2]*dir[2]<0) return 0.0;
return TGeoShape::Big();
}
// check if on Rmax boundary
if (safrmax<safrmin && safrmax<safphi) {
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg2*dir[2]*r;
if (ddotn<=0) return 0.0;
return TGeoShape::Big();
}
// check if on phi boundary
if (safphi<safrmin) {
// We may cross again a phi of rmin boundary
// check first if we are on phi1 or phi2
Double_t un;
if (TMath::Abs(point[1]-s1*r) < TMath::Abs(point[1]-s2*r)) {
un = dir[0]*s1-dir[1]*c1;
if (un < 0) return 0.0;
if (cdfi>=0) return TGeoShape::Big();
un = -dir[0]*s2+dir[1]*c2;
if (un<0) {
s = -point[0]*s2+point[1]*c2;
if (s>0) {
s /= (-un);
zi = point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi = point[0]+s*dir[0];
yi = point[1]+s*dir[1];
if ((yi*cm-xi*sm)>0) {
r2=xi*xi+yi*yi;
rin = ro1+tg1*zi;
rout = ro2+tg2*zi;
if ((rin*rin<=r2) && (rout*rout>=r2)) return s;
}
}
}
}
} else {
un = -dir[0]*s2+dir[1]*c2;
if (un < 0) return 0.0;
if (cdfi>=0) return TGeoShape::Big();
un = dir[0]*s1-dir[1]*c1;
if (un<0) {
s = point[0]*s1-point[1]*c1;
if (s>0) {
s /= (-un);
zi = point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi = point[0]+s*dir[0];
yi = point[1]+s*dir[1];
if ((yi*cm-xi*sm)<0) {
r2=xi*xi+yi*yi;
rin = ro1+tg1*zi;
rout = ro2+tg2*zi;
if ((rin*rin<=r2) && (rout*rout>=r2)) return s;
}
}
}
}
}
// We may also cross rmin, second solution coming from outside
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg1*dir[2]*r;
if (ddotn>=0) return TGeoShape::Big();
if (cdfi>=0) return TGeoShape::Big();
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta<0) return TGeoShape::Big();
snxt = -b-delta;
if (snxt<0) return TGeoShape::Big();
snxt = -b+delta;
zi = point[2]+snxt*dir[2];
if (TMath::Abs(zi)>dz) return TGeoShape::Big();
xi = point[0]+snxt*dir[0];
yi = point[1]+snxt*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) return snxt;
return TGeoShape::Big();
}
// We are on rmin boundary: we may cross again rmin or a phi facette
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg1*dir[2]*r;
if (ddotn>=0) return 0.0;
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta<0) return 0.0;
snxt = -b+delta;
if (snxt<0) return TGeoShape::Big();
if (TMath::Abs(-b-delta)>snxt) return TGeoShape::Big();
zi = point[2]+snxt*dir[2];
if (TMath::Abs(zi)>dz) return TGeoShape::Big();
// OK, we cross rmin at snxt - check if within phi range
xi = point[0]+snxt*dir[0];
yi = point[1]+snxt*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) return snxt;
// we cross rmin in the phi gap - we may cross a phi facette
if (cdfi>=0) return TGeoShape::Big();
Double_t un=-dir[0]*s1+dir[1]*c1;
if (un > 0) {
s=point[0]*s1-point[1]*c1;
if (s>=0) {
s /= un;
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
if ((yi*cm-xi*sm)<=0) {
r2=xi*xi+yi*yi;
rin = ro1+tg1*zi;
rout = ro2+tg2*zi;
if ((rin*rin<=r2) && (rout*rout>=r2)) return s;
}
}
}
}
un=dir[0]*s2-dir[1]*c2;
if (un > 0) {
s=(point[1]*c2-point[0]*s2)/un;
if (s>=0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
if ((yi*cm-xi*sm)>=0) {
r2=xi*xi+yi*yi;
rin = ro1+tg1*zi;
rout = ro2+tg2*zi;
if ((rin*rin<=r2) && (rout*rout>=r2)) return s;
}
}
}
}
return TGeoShape::Big();
}
// The point is really outside
Double_t sr1 = TGeoShape::Big();
if (!inrmax) {
// check crossing with outer cone
TGeoCone::DistToCone(point, dir, dz, rmax1, rmax2, b, delta);
if (delta>=0) {
s = -b-delta;
if (s>0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) return s; // rmax crossing
}
}
s = -b+delta;
if (s>0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) sr1=s;
}
}
}
}
// check crossing with inner cone
Double_t sr2 = TGeoShape::Big();
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta>=0) {
s = -b-delta;
if (s>0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) sr2=s;
}
}
if (sr2>1E10) {
s = -b+delta;
if (s>0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) sr2=s;
}
}
}
}
snxt = TMath::Min(sr1,sr2);
// Check phi crossing
s = TGeoShape::DistToPhiMin(point,dir,s1,c1,s2,c2,sm,cm,kFALSE);
if (s>snxt) return snxt;
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)>dz) return snxt;
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
rout = ro2+tg2*zi;
if (r2>rout*rout) return snxt;
rin = ro1+tg1*zi;
if (r2>=rin*rin) return s; // phi crossing
return snxt;
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistFromOutside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from outside point to surface of the tube
// compute safe radius
if (iact<3 && safe) {
*safe = Safety(point, kFALSE);
if (iact==0) return TGeoShape::Big();
if ((iact==1) && (*safe>step)) return TGeoShape::Big();
}
Double_t phi1 = fPhi1*TMath::DegToRad();
Double_t phi2 = fPhi2*TMath::DegToRad();
Double_t c1 = TMath::Cos(phi1);
Double_t c2 = TMath::Cos(phi2);
Double_t s1 = TMath::Sin(phi1);
Double_t s2 = TMath::Sin(phi2);
Double_t phim = 0.5*(phi1+phi2);
Double_t cm = TMath::Cos(phim);
Double_t sm = TMath::Sin(phim);
Double_t dfi = 0.5*(phi2-phi1);
Double_t cdfi = TMath::Cos(dfi);
return TGeoConeSeg::DistFromOutsideS(point,dir,fDz,fRmin1,fRmax1,fRmin2,fRmax2,c1,s1,c2,s2,cm,sm,cdfi);
}
//_____________________________________________________________________________
Int_t TGeoConeSeg::DistancetoPrimitive(Int_t px, Int_t py)
{
// compute closest distance from point px,py to each corner
Int_t n = gGeoManager->GetNsegments()+1;
const Int_t numPoints = 4*n;
return ShapeDistancetoPrimitive(numPoints, px, py);
}
//_____________________________________________________________________________
TGeoVolume *TGeoConeSeg::Divide(TGeoVolume *voldiv, const char *divname, Int_t iaxis, Int_t ndiv,
Double_t start, Double_t step)
{
//--- Divide this cone segment shape belonging to volume "voldiv" into ndiv volumes
// called divname, from start position with the given step. Returns pointer
// to created division cell volume in case of Z divisions. For Z division
// creates all volumes with different shapes and returns pointer to volume that
// was divided. In case a wrong division axis is supplied, returns pointer to
// volume that was divided.
TGeoShape *shape; //--- shape to be created
TGeoVolume *vol; //--- division volume to be created
TGeoVolumeMulti *vmulti; //--- generic divided volume
TGeoPatternFinder *finder; //--- finder to be attached
TString opt = ""; //--- option to be attached
Double_t dphi;
Int_t id;
Double_t end = start+ndiv*step;
switch (iaxis) {
case 1: //--- R division
Error("Divide","division of a cone segment on R not implemented");
return 0;
case 2: //--- Phi division
dphi = fPhi2-fPhi1;
if (dphi<0) dphi+=360.;
finder = new TGeoPatternCylPhi(voldiv, ndiv, start, end);
voldiv->SetFinder(finder);
finder->SetDivIndex(voldiv->GetNdaughters());
shape = new TGeoConeSeg(fDz, fRmin1, fRmax1, fRmin2, fRmax2, -step/2, step/2);
vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
vmulti->AddVolume(vol);
opt = "Phi";
for (id=0; id<ndiv; id++) {
voldiv->AddNodeOffset(vol, id, start+id*step+step/2, opt.Data());
((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);
}
return vmulti;
case 3: //--- Z division
finder = new TGeoPatternZ(voldiv, ndiv, start, end);
vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
voldiv->SetFinder(finder);
finder->SetDivIndex(voldiv->GetNdaughters());
for (id=0; id<ndiv; id++) {
Double_t z1 = start+id*step;
Double_t z2 = start+(id+1)*step;
Double_t rmin1n = 0.5*(fRmin1*(fDz-z1)+fRmin2*(fDz+z1))/fDz;
Double_t rmax1n = 0.5*(fRmax1*(fDz-z1)+fRmax2*(fDz+z1))/fDz;
Double_t rmin2n = 0.5*(fRmin1*(fDz-z2)+fRmin2*(fDz+z2))/fDz;
Double_t rmax2n = 0.5*(fRmax1*(fDz-z2)+fRmax2*(fDz+z2))/fDz;
shape = new TGeoConeSeg(step/2, rmin1n, rmax1n, rmin2n, rmax2n, fPhi1, fPhi2);
vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
vmulti->AddVolume(vol);
opt = "Z";
voldiv->AddNodeOffset(vol, id, start+id*step+step/2, opt.Data());
((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);
}
return vmulti;
default:
Error("Divide", "Wrong axis type for division");
return 0;
}
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::GetAxisRange(Int_t iaxis, Double_t &xlo, Double_t &xhi) const
{
// Get range of shape for a given axis.
xlo = 0;
xhi = 0;
Double_t dx = 0;
switch (iaxis) {
case 2:
xlo = fPhi1;
xhi = fPhi2;
dx = xhi-xlo;
return dx;
case 3:
xlo = -fDz;
xhi = fDz;
dx = xhi-xlo;
return dx;
}
return dx;
}
//_____________________________________________________________________________
void TGeoConeSeg::GetBoundingCylinder(Double_t *param) const
{
//--- Fill vector param[4] with the bounding cylinder parameters. The order
// is the following : Rmin, Rmax, Phi1, Phi2
param[0] = TMath::Min(fRmin1, fRmin2); // Rmin
param[0] *= param[0];
param[1] = TMath::Max(fRmax1, fRmax2); // Rmax
param[1] *= param[1];
param[2] = (fPhi1<0)?(fPhi1+360.):fPhi1; // Phi1
param[3] = fPhi2; // Phi2
while (param[3]<param[2]) param[3]+=360.;
}
//_____________________________________________________________________________
TGeoShape *TGeoConeSeg::GetMakeRuntimeShape(TGeoShape *mother, TGeoMatrix * /*mat*/) const
{
// in case shape has some negative parameters, these has to be computed
// in order to fit the mother
if (!TestShapeBit(kGeoRunTimeShape)) return 0;
if (!mother->TestShapeBit(kGeoConeSeg)) {
Error("GetMakeRuntimeShape", "invalid mother");
return 0;
}
Double_t rmin1, rmax1, rmin2, rmax2, dz;
rmin1 = fRmin1;
rmax1 = fRmax1;
rmin2 = fRmin2;
rmax2 = fRmax2;
dz = fDz;
if (fDz<0) dz=((TGeoCone*)mother)->GetDz();
if (fRmin1<0)
rmin1 = ((TGeoCone*)mother)->GetRmin1();
if ((fRmax1<0) || (fRmax1<fRmin1))
rmax1 = ((TGeoCone*)mother)->GetRmax1();
if (fRmin2<0)
rmin2 = ((TGeoCone*)mother)->GetRmin2();
if ((fRmax2<0) || (fRmax2<fRmin2))
rmax2 = ((TGeoCone*)mother)->GetRmax2();
return (new TGeoConeSeg(GetName(), dz, rmin1, rmax1, rmin2, rmax2, fPhi1, fPhi2));
}
//_____________________________________________________________________________
void TGeoConeSeg::InspectShape() const
{
// print shape parameters
printf("*** Shape %s: TGeoConeSeg ***\n", GetName());
printf(" dz = %11.5f\n", fDz);
printf(" Rmin1 = %11.5f\n", fRmin1);
printf(" Rmax1 = %11.5f\n", fRmax1);
printf(" Rmin2 = %11.5f\n", fRmin2);
printf(" Rmax2 = %11.5f\n", fRmax2);
printf(" phi1 = %11.5f\n", fPhi1);
printf(" phi2 = %11.5f\n", fPhi2);
printf(" Bounding box:\n");
TGeoBBox::InspectShape();
}
//_____________________________________________________________________________
TBuffer3D *TGeoConeSeg::MakeBuffer3D() const
{
// Creates a TBuffer3D describing *this* shape.
// Coordinates are in local reference frame.
Int_t n = gGeoManager->GetNsegments()+1;
Int_t nbPnts = 4*n;
Int_t nbSegs = 2*nbPnts;
Int_t nbPols = nbPnts-2;
TBuffer3D* buff = new TBuffer3D(TBuffer3DTypes::kGeneric,
nbPnts, 3*nbPnts,
nbSegs, 3*nbSegs,
nbPols, 6*nbPols);
if (buff)
{
SetPoints(buff->fPnts);
SetSegsAndPols(*buff);
}
return buff;
}
//_____________________________________________________________________________
void TGeoConeSeg::SetSegsAndPols(TBuffer3D &buffer) const
{
// Fill TBuffer3D structure for segments and polygons.
Int_t i, j;
Int_t n = gGeoManager->GetNsegments()+1;
Int_t c = GetBasicColor();
memset(buffer.fSegs, 0, buffer.NbSegs()*3*sizeof(Int_t));
for (i = 0; i < 4; i++) {
for (j = 1; j < n; j++) {
buffer.fSegs[(i*n+j-1)*3 ] = c;
buffer.fSegs[(i*n+j-1)*3+1] = i*n+j-1;
buffer.fSegs[(i*n+j-1)*3+2] = i*n+j;
}
}
for (i = 4; i < 6; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c+1;
buffer.fSegs[(i*n+j)*3+1] = (i-4)*n+j;
buffer.fSegs[(i*n+j)*3+2] = (i-2)*n+j;
}
}
for (i = 6; i < 8; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c;
buffer.fSegs[(i*n+j)*3+1] = 2*(i-6)*n+j;
buffer.fSegs[(i*n+j)*3+2] = (2*(i-6)+1)*n+j;
}
}
Int_t indx = 0;
memset(buffer.fPols, 0, buffer.NbPols()*6*sizeof(Int_t));
i = 0;
for (j = 0; j < n-1; j++) {
buffer.fPols[indx++] = c;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = (4+i)*n+j+1;
buffer.fPols[indx++] = (2+i)*n+j;
buffer.fPols[indx++] = (4+i)*n+j;
buffer.fPols[indx++] = i*n+j;
}
i = 1;
for (j = 0; j < n-1; j++) {
buffer.fPols[indx++] = c;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = i*n+j;
buffer.fPols[indx++] = (4+i)*n+j;
buffer.fPols[indx++] = (2+i)*n+j;
buffer.fPols[indx++] = (4+i)*n+j+1;
}
i = 2;
for (j = 0; j < n-1; j++) {
buffer.fPols[indx++] = c+i;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = (i-2)*2*n+j;
buffer.fPols[indx++] = (4+i)*n+j;
buffer.fPols[indx++] = ((i-2)*2+1)*n+j;
buffer.fPols[indx++] = (4+i)*n+j+1;
}
i = 3;
for (j = 0; j < n-1; j++) {
buffer.fPols[indx++] = c+i;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = (4+i)*n+j+1;
buffer.fPols[indx++] = ((i-2)*2+1)*n+j;
buffer.fPols[indx++] = (4+i)*n+j;
buffer.fPols[indx++] = (i-2)*2*n+j;
}
buffer.fPols[indx++] = c+2;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = 6*n;
buffer.fPols[indx++] = 4*n;
buffer.fPols[indx++] = 7*n;
buffer.fPols[indx++] = 5*n;
buffer.fPols[indx++] = c+2;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = 6*n-1;
buffer.fPols[indx++] = 8*n-1;
buffer.fPols[indx++] = 5*n-1;
buffer.fPols[indx++] = 7*n-1;
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::Safety(Double_t *point, Bool_t in) const
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
Double_t saf[3];
Double_t ro1 = 0.5*(fRmin1+fRmin2);
Double_t tg1 = 0.5*(fRmin2-fRmin1)/fDz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(fRmax1+fRmax2);
Double_t tg2 = 0.5*(fRmax2-fRmax1)/fDz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
Double_t safe = TGeoShape::Big();
if (in) {
saf[0] = fDz-TMath::Abs(point[2]);
saf[1] = (r-rin)*cr1;
saf[2] = (rout-r)*cr2;
safe = saf[TMath::LocMin(3,saf)];
} else {
saf[0] = TMath::Abs(point[2])-fDz; // positive if inside
saf[1] = (rin-r)*cr1;
saf[2] = (r-rout)*cr2;
safe = saf[TMath::LocMax(3,saf)];
}
Double_t safphi = TGeoShape::SafetyPhi(point, in, fPhi1, fPhi2);
if (in) return TMath::Min(safe, safphi);
return TMath::Max(safe, safphi);
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::SafetyS(Double_t *point, Bool_t in, Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Double_t phi1, Double_t phi2, Int_t skipz)
{
// Static method to compute the closest distance from given point to this shape.
Double_t saf[3];
Double_t ro1 = 0.5*(rmin1+rmin2);
Double_t tg1 = 0.5*(rmin2-rmin1)/dz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(rmax1+rmax2);
Double_t tg2 = 0.5*(rmax2-rmax1)/dz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
Double_t safe = TGeoShape::Big();
switch (skipz) {
case 1: // skip lower Z plane
saf[0] = dz - point[2];
break;
case 2: // skip upper Z plane
saf[0] = dz + point[2];
break;
case 3: // skip both
saf[0] = TGeoShape::Big();
default:
saf[0] = dz-TMath::Abs(point[2]);
}
saf[1] = (r-rin)*cr1;
saf[2] = (rout-r)*cr2;
Double_t safphi = TGeoShape::SafetyPhi(point,in,phi1,phi2);
if (in) {
safe = saf[TMath::LocMin(3,saf)];
return TMath::Min(safe,safphi);
}
for (Int_t i=0; i<3; i++) saf[i]=-saf[i];
safe = saf[TMath::LocMax(3,saf)];
return TMath::Max(safe,safphi);
}
//_____________________________________________________________________________
void TGeoConeSeg::SavePrimitive(ofstream &out, Option_t * /*option*/)
{
// Save a primitive as a C++ statement(s) on output stream "out".
if (TObject::TestBit(kGeoSavePrimitive)) return;
out << " // Shape: " << GetName() << " type: " << ClassName() << endl;
out << " dz = " << fDz << ";" << endl;
out << " rmin1 = " << fRmin1 << ";" << endl;
out << " rmax1 = " << fRmax1 << ";" << endl;
out << " rmin2 = " << fRmin2 << ";" << endl;
out << " rmax2 = " << fRmax2 << ";" << endl;
out << " phi1 = " << fPhi1 << ";" << endl;
out << " phi2 = " << fPhi2 << ";" << endl;
out << " TGeoShape *" << GetPointerName() << " = new TGeoConeSeg(\"" << GetName() << "\", dz,rmin1,rmax1,rmin2,rmax2,phi1,phi2);" << endl;
TObject::SetBit(TGeoShape::kGeoSavePrimitive);
}
//_____________________________________________________________________________
void TGeoConeSeg::SetConsDimensions(Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Double_t phi1, Double_t phi2)
{
fDz = dz;
fRmin1 = rmin1;
fRmax1 = rmax1;
fRmin2 = rmin2;
fRmax2 = rmax2;
fPhi1 = phi1;
if (fPhi1<0) fPhi1+=360.;
fPhi2 = phi2;
while (fPhi2<fPhi1) fPhi2+=360.;
}
//_____________________________________________________________________________
void TGeoConeSeg::SetDimensions(Double_t *param)
{
Double_t dz = param[0];
Double_t rmin1 = param[1];
Double_t rmax1 = param[2];
Double_t rmin2 = param[3];
Double_t rmax2 = param[4];
Double_t phi1 = param[5];
Double_t phi2 = param[6];
SetConsDimensions(dz, rmin1, rmax1,rmin2, rmax2, phi1, phi2);
}
//_____________________________________________________________________________
void TGeoConeSeg::SetPoints(Double_t *points) const
{
// create cone segment mesh points
Int_t j, n;
Float_t dphi,phi,phi1, phi2,dz;
n = gGeoManager->GetNsegments()+1;
dz = fDz;
phi1 = fPhi1;
phi2 = fPhi2;
dphi = (phi2-phi1)/(n-1);
Int_t indx = 0;
if (points) {
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmin1 * TMath::Cos(phi);
points[indx++] = fRmin1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmax1 * TMath::Cos(phi);
points[indx++] = fRmax1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmin2 * TMath::Cos(phi);
points[indx++] = fRmin2 * TMath::Sin(phi);
points[indx++] = dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmax2 * TMath::Cos(phi);
points[indx++] = fRmax2 * TMath::Sin(phi);
points[indx++] = dz;
}
}
}
//_____________________________________________________________________________
void TGeoConeSeg::SetPoints(Float_t *points) const
{
// create cone segment mesh points
Int_t j, n;
Float_t dphi,phi,phi1, phi2,dz;
n = gGeoManager->GetNsegments()+1;
dz = fDz;
phi1 = fPhi1;
phi2 = fPhi2;
dphi = (phi2-phi1)/(n-1);
Int_t indx = 0;
if (points) {
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmin1 * TMath::Cos(phi);
points[indx++] = fRmin1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmax1 * TMath::Cos(phi);
points[indx++] = fRmax1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmin2 * TMath::Cos(phi);
points[indx++] = fRmin2 * TMath::Sin(phi);
points[indx++] = dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmax2 * TMath::Cos(phi);
points[indx++] = fRmax2 * TMath::Sin(phi);
points[indx++] = dz;
}
}
}
//_____________________________________________________________________________
Int_t TGeoConeSeg::GetNmeshVertices() const
{
// Return number of vertices of the mesh representation
Int_t n = gGeoManager->GetNsegments()+1;
Int_t numPoints = n*4;
return numPoints;
}
//_____________________________________________________________________________
void TGeoConeSeg::Sizeof3D() const
{
///// fill size of this 3-D object
/// TVirtualGeoPainter *painter = gGeoManager->GetGeomPainter();
/// if (!painter) return;
///
/// Int_t n = gGeoManager->GetNsegments()+1;
///
/// Int_t numPoints = n*4;
/// Int_t numSegs = n*8;
/// Int_t numPolys = n*4-2;
/// painter->AddSize3D(numPoints, numSegs, numPolys);
}
//_____________________________________________________________________________
const TBuffer3D & TGeoConeSeg::GetBuffer3D(Int_t reqSections, Bool_t localFrame) const
{
static TBuffer3D buffer(TBuffer3DTypes::kGeneric);
TGeoBBox::FillBuffer3D(buffer, reqSections, localFrame);
if (reqSections & TBuffer3D::kRawSizes) {
Int_t n = gGeoManager->GetNsegments()+1;
Int_t nbPnts = 4*n;
Int_t nbSegs = 2*nbPnts;
Int_t nbPols = nbPnts-2;
if (buffer.SetRawSizes(nbPnts, 3*nbPnts, nbSegs, 3*nbSegs, nbPols, 6*nbPols)) {
buffer.SetSectionsValid(TBuffer3D::kRawSizes);
}
}
if ((reqSections & TBuffer3D::kRaw) && buffer.SectionsValid(TBuffer3D::kRawSizes)) {
SetPoints(buffer.fPnts);
if (!buffer.fLocalFrame) {
TransformPoints(buffer.fPnts, buffer.NbPnts());
}
SetSegsAndPols(buffer);
buffer.SetSectionsValid(TBuffer3D::kRaw);
}
return buffer;
}
*/
//
#include "Riostream.h"
#include "TROOT.h"
#include "TGeoManager.h"
#include "TGeoVolume.h"
#include "TVirtualGeoPainter.h"
#include "TGeoCone.h"
#include "TVirtualPad.h"
#include "TBuffer3D.h"
#include "TBuffer3DTypes.h"
ClassImp(TGeoCone)
//_____________________________________________________________________________
TGeoCone::TGeoCone()
{
// Default constructor
SetShapeBit(TGeoShape::kGeoCone);
fDz = 0.0;
fRmin1 = 0.0;
fRmax1 = 0.0;
fRmin2 = 0.0;
fRmax2 = 0.0;
}
//_____________________________________________________________________________
TGeoCone::TGeoCone(Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2)
:TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoCone);
SetConeDimensions(dz, rmin1, rmax1, rmin2, rmax2);
if ((dz<0) || (rmin1<0) || (rmax1<0) || (rmin2<0) || (rmax2<0)) {
SetShapeBit(kGeoRunTimeShape);
}
else ComputeBBox();
}
//_____________________________________________________________________________
TGeoCone::TGeoCone(const char *name, Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2)
:TGeoBBox(name, 0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoCone);
SetConeDimensions(dz, rmin1, rmax1, rmin2, rmax2);
if ((dz<0) || (rmin1<0) || (rmax1<0) || (rmin2<0) || (rmax2<0)) {
SetShapeBit(kGeoRunTimeShape);
}
else ComputeBBox();
}
//_____________________________________________________________________________
TGeoCone::TGeoCone(Double_t *param)
:TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
// param[0] = dz
// param[1] = Rmin1
// param[2] = Rmax1
// param[3] = Rmin2
// param[4] = Rmax2
SetShapeBit(TGeoShape::kGeoCone);
SetDimensions(param);
if ((fDz<0) || (fRmin1<0) || (fRmax1<0) || (fRmin2<0) || (fRmax2<0))
SetShapeBit(kGeoRunTimeShape);
else ComputeBBox();
}
//_____________________________________________________________________________
TGeoCone::~TGeoCone()
{
// destructor
}
//_____________________________________________________________________________
void TGeoCone::ComputeBBox()
{
// compute bounding box of the sphere
TGeoBBox *box = (TGeoBBox*)this;
box->SetBoxDimensions(TMath::Max(fRmax1, fRmax2), TMath::Max(fRmax1, fRmax2), fDz);
memset(fOrigin, 0, 3*sizeof(Double_t));
}
//_____________________________________________________________________________
void TGeoCone::ComputeNormal(Double_t *point, Double_t *dir, Double_t *norm)
{
// Compute normal to closest surface from POINT.
Double_t safr,safe,phi;
memset(norm,0,3*sizeof(Double_t));
phi = TMath::ATan2(point[1],point[0]);
Double_t cphi = TMath::Cos(phi);
Double_t sphi = TMath::Sin(phi);
Double_t ro1 = 0.5*(fRmin1+fRmin2);
Double_t tg1 = 0.5*(fRmin2-fRmin1)/fDz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(fRmax1+fRmax2);
Double_t tg2 = 0.5*(fRmax2-fRmax1)/fDz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
safe = TMath::Abs(fDz-TMath::Abs(point[2]));
norm[2] = 1;
safr = (ro1>0)?(TMath::Abs((r-rin)*cr1)):TGeoShape::Big();
if (safr<safe) {
safe = safr;
norm[0] = cr1*cphi;
norm[1] = cr1*sphi;
norm[2] = -tg1*cr1;
}
safr = TMath::Abs((rout-r)*cr2);
if (safr<safe) {
norm[0] = cr2*cphi;
norm[1] = cr2*sphi;
norm[2] = -tg2*cr2;
}
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
void TGeoCone::ComputeNormalS(Double_t *point, Double_t *dir, Double_t *norm,
Double_t dz, Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2)
{
// Compute normal to closest surface from POINT.
Double_t safe,phi;
memset(norm,0,3*sizeof(Double_t));
phi = TMath::ATan2(point[1],point[0]);
Double_t cphi = TMath::Cos(phi);
Double_t sphi = TMath::Sin(phi);
Double_t ro1 = 0.5*(rmin1+rmin2);
Double_t tg1 = 0.5*(rmin2-rmin1)/dz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(rmax1+rmax2);
Double_t tg2 = 0.5*(rmax2-rmax1)/dz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
safe = (ro1>0)?(TMath::Abs((r-rin)*cr1)):TGeoShape::Big();
norm[0] = cr1*cphi;
norm[1] = cr1*sphi;
norm[2] = -tg1*cr1;
if (TMath::Abs((rout-r)*cr2)<safe) {
norm[0] = cr2*cphi;
norm[1] = cr2*sphi;
norm[2] = -tg2*cr2;
}
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
Bool_t TGeoCone::Contains(Double_t *point) const
{
// test if point is inside this cone
if (TMath::Abs(point[2]) > fDz) return kFALSE;
Double_t r2 = point[0]*point[0]+point[1]*point[1];
Double_t rl = 0.5*(fRmin2*(point[2]+fDz)+fRmin1*(fDz-point[2]))/fDz;
Double_t rh = 0.5*(fRmax2*(point[2]+fDz)+fRmax1*(fDz-point[2]))/fDz;
if ((r2<rl*rl) || (r2>rh*rh)) return kFALSE;
return kTRUE;
}
//_____________________________________________________________________________
Double_t TGeoCone::DistFromInsideS(Double_t *point, Double_t *dir, Double_t dz,
Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2)
{
// Compute distance from inside point to surface of the cone (static)
// Boundary safe algorithm.
if (dz<=0) return TGeoShape::Big();
// compute distance to surface
// Do Z
Double_t sz = TGeoShape::Big();
if (dir[2]) {
sz = (TMath::Sign(dz, dir[2])-point[2])/dir[2];
if (sz<=0) return 0.0;
}
Double_t rsq=point[0]*point[0]+point[1]*point[1];
Double_t zinv = 1./dz;
Double_t rin = 0.5*(rmin1+rmin2+(rmin2-rmin1)*point[2]*zinv);
// Do Rmin
Double_t sr = TGeoShape::Big();
Double_t b,delta,zi;
if (rin>0) {
// Protection in case point is actually outside the cone
if (rsq < rin*(rin+TGeoShape::Tolerance())) {
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]+0.5*(rmin1-rmin2)*dir[2]*zinv*TMath::Sqrt(rsq);
if (ddotn<=0) return 0.0;
} else {
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta>0) {
sr = -b-delta;
if (sr>0) {
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
}
sr = -b+delta;
if (sr>0) {
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
}
}
}
}
// Do Rmax
Double_t rout = 0.5*(rmax1+rmax2+(rmax2-rmax1)*point[2]*zinv);
if (rsq > rout*(rout-TGeoShape::Tolerance())) {
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]+0.5*(rmax1-rmax2)*dir[2]*zinv*TMath::Sqrt(rsq);
if (ddotn>=0) return 0.0;
TGeoCone::DistToCone(point, dir, dz, rmax1, rmax2, b, delta);
if (delta<0) return 0.0;
sr = -b+delta;
if (sr<0) return sz;
if (TMath::Abs(-b-delta)>sr) return sz;
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
return sz;
}
TGeoCone::DistToCone(point, dir, dz, rmax1, rmax2, b, delta);
if (delta>0) {
sr = -b-delta;
if (sr>0) {
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
}
sr = -b+delta;
if (sr>TGeoShape::Tolerance()) {
zi = point[2]+sr*dir[2];
if (TMath::Abs(zi)<=dz) return TMath::Min(sz,sr);
}
}
return sz;
}
//_____________________________________________________________________________
Double_t TGeoCone::DistFromInside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// Compute distance from inside point to surface of the cone
// Boundary safe algorithm.
if (iact<3 && safe) {
*safe = Safety(point, kTRUE);
if (iact==0) return TGeoShape::Big();
if ((iact==1) && (*safe>step)) return TGeoShape::Big();
}
// compute distance to surface
return TGeoCone::DistFromInsideS(point, dir, fDz, fRmin1, fRmax1, fRmin2, fRmax2);
}
//_____________________________________________________________________________
Double_t TGeoCone::DistFromOutsideS(Double_t *point, Double_t *dir, Double_t dz,
Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2)
{
// Compute distance from outside point to surface of the tube
// Boundary safe algorithm.
// compute distance to Z planes
if (dz<=0) return TGeoShape::Big();
Double_t snxt;
Double_t xp, yp, zp;
Bool_t inz = kTRUE;
if (point[2]<=-dz) {
if (dir[2]<=0) return TGeoShape::Big();
snxt = (-dz-point[2])/dir[2];
xp = point[0]+snxt*dir[0];
yp = point[1]+snxt*dir[1];
Double_t r2 = xp*xp+yp*yp;
if ((r2>=rmin1*rmin1) && (r2<=rmax1*rmax1)) return snxt;
inz = kFALSE;
} else {
if (point[2]>=dz) {
if (dir[2]>=0) return TGeoShape::Big();
snxt = (dz-point[2])/dir[2];
xp = point[0]+snxt*dir[0];
yp = point[1]+snxt*dir[1];
Double_t r2 = xp*xp+yp*yp;
if ((r2>=rmin2*rmin2) && (r2<=rmax2*rmax2)) return snxt;
inz = kFALSE;
}
}
Double_t rsq = point[0]*point[0]+point[1]*point[1];
Double_t dzinv = 1./dz;
Double_t ro1=0.5*(rmin1+rmin2);
Bool_t hasrmin = (ro1>0)?kTRUE:kFALSE;
Double_t tg1 = 0.;
Double_t rin = 0.;
Bool_t inrmin = kTRUE; // r>=rmin
if (hasrmin) {
tg1=0.5*(rmin2-rmin1)*dzinv;
rin=ro1+tg1*point[2];
if (rin>0 && rsq<rin*(rin-TGeoShape::Tolerance())) inrmin=kFALSE;
}
Double_t ro2=0.5*(rmax1+rmax2);
Double_t tg2=0.5*(rmax2-rmax1)*dzinv;
Double_t rout=tg2*point[2]+ro2;
Bool_t inrmax = kFALSE;
if (rout>0 && rsq<rout*(rout+TGeoShape::Tolerance())) inrmax=kTRUE;
Bool_t in = inz & inrmin & inrmax;
Double_t b,delta;
// If inside cone, we are most likely on a boundary within machine precision.
if (in) {
Double_t r=TMath::Sqrt(rsq);
Double_t safz = dz-TMath::Abs(point[2]); // positive
Double_t safrmin = (hasrmin)?(r-rin):TGeoShape::Big();
Double_t safrmax = rout - r;
if (safz<=safrmin && safz<=safrmax) {
// on Z boundary
if (point[2]*dir[2]<0) return 0.0;
return TGeoShape::Big();
}
if (safrmax<safrmin) {
// on rmax boundary
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg2*dir[2]*r;
if (ddotn<=0) return 0.0;
return TGeoShape::Big();
}
// on rmin boundary
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg1*dir[2]*r;
if (ddotn>=0) return 0.0;
// we can cross (+) solution of rmin
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta<0) return 0.0;
snxt = -b+delta;
if (snxt<0) return TGeoShape::Big();
if (TMath::Abs(-b-delta)>snxt) return TGeoShape::Big();
zp = point[2]+snxt*dir[2];
if (TMath::Abs(zp)<=dz) return snxt;
return TGeoShape::Big();
}
// compute distance to inner cone
snxt = TGeoShape::Big();
if (!inrmin) {
// ray can cross only inner cone
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta<0) return TGeoShape::Big();
snxt = -b+delta;
if (snxt<=0) return TGeoShape::Big();
zp = point[2]+snxt*dir[2];
if (TMath::Abs(zp)<=dz) return snxt;
snxt = -b-delta;
if (snxt<=0) return TGeoShape::Big();
zp = point[2]+snxt*dir[2];
if (TMath::Abs(zp)<=dz) return snxt;
return TGeoShape::Big();
} else {
if (hasrmin) {
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta>0) {
Double_t din = -b+delta;
if (din>0) {
zp = point[2]+din*dir[2];
if (TMath::Abs(zp)<=dz) snxt = din;
}
}
}
}
if (inrmax) return snxt;
// we can cross only outer cone, both solutions possible
// compute distance to outer cone
TGeoCone::DistToCone(point, dir, dz, rmax1, rmax2, b, delta);
if (delta<0) return snxt;
Double_t dout = -b-delta;
if (dout>0 && dout<snxt) {
zp = point[2]+dout*dir[2];
if (TMath::Abs(zp)<=dz) return dout;
}
dout = -b+delta;
if (dout<=0 || dout>snxt) return snxt;
zp = point[2]+dout*dir[2];
if (TMath::Abs(zp)<=dz) return dout;
return snxt;
}
//_____________________________________________________________________________
Double_t TGeoCone::DistFromOutside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from outside point to surface of the tube
// compute safe radius
if (iact<3 && safe) {
*safe = Safety(point, kFALSE);
if (iact==0) return TGeoShape::Big();
if ((iact==1) && (*safe>step)) return TGeoShape::Big();
}
// compute distance to Z planes
return TGeoCone::DistFromOutsideS(point, dir, fDz, fRmin1, fRmax1, fRmin2, fRmax2);
}
//_____________________________________________________________________________
void TGeoCone::DistToCone(Double_t *point, Double_t *dir, Double_t dz, Double_t r1, Double_t r2,
Double_t &b, Double_t &delta)
{
// Static method to compute distance to a conical surface with :
// - r1, z1 - radius and Z position of lower base
// - r2, z2 - radius and Z position of upper base
delta = -1.;
if (dz<0) return;
Double_t ro0 = 0.5*(r1+r2);
Double_t tz = 0.5*(r2-r1)/dz;
Double_t rsq = point[0]*point[0] + point[1]*point[1];
Double_t rc = ro0 + point[2]*tz;
Double_t a = dir[0]*dir[0] + dir[1]*dir[1] - tz*tz*dir[2]*dir[2];
b = point[0]*dir[0] + point[1]*dir[1] - tz*rc*dir[2];
Double_t c = rsq - rc*rc;
if (a==0) {
if (b==0) return;
b = 0.5*c/b;
return;
}
a = 1./a;
b *= a;
c *= a;
delta = b*b - c;
if (delta>0) {
delta = TMath::Sqrt(delta);
} else {
delta = -1.;
}
}
//_____________________________________________________________________________
Int_t TGeoCone::DistancetoPrimitive(Int_t px, Int_t py)
{
// compute closest distance from point px,py to each corner
Int_t n = gGeoManager->GetNsegments();
const Int_t numPoints = 4*n;
return ShapeDistancetoPrimitive(numPoints, px, py);
}
//_____________________________________________________________________________
TGeoVolume *TGeoCone::Divide(TGeoVolume *voldiv, const char *divname, Int_t iaxis, Int_t ndiv,
Double_t start, Double_t step)
{
//--- Divide this cone shape belonging to volume "voldiv" into ndiv volumes
// called divname, from start position with the given step. Returns pointer
// to created division cell volume in case of Z divisions. For Z division
// creates all volumes with different shapes and returns pointer to volume that
// was divided. In case a wrong division axis is supplied, returns pointer to
// volume that was divided.
TGeoShape *shape; //--- shape to be created
TGeoVolume *vol; //--- division volume to be created
TGeoVolumeMulti *vmulti; //--- generic divided volume
TGeoPatternFinder *finder; //--- finder to be attached
TString opt = ""; //--- option to be attached
Int_t id;
Double_t end = start+ndiv*step;
switch (iaxis) {
case 1: //--- R division
Error("Divide","division of a cone on R not implemented");
return 0;
case 2: // --- Phi division
finder = new TGeoPatternCylPhi(voldiv, ndiv, start, end);
voldiv->SetFinder(finder);
finder->SetDivIndex(voldiv->GetNdaughters());
shape = new TGeoConeSeg(fDz, fRmin1, fRmax1, fRmin2, fRmax2, -step/2, step/2);
vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
vmulti->AddVolume(vol);
opt = "Phi";
for (id=0; id<ndiv; id++) {
voldiv->AddNodeOffset(vol, id, start+id*step+step/2, opt.Data());
((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);
}
return vmulti;
case 3: //--- Z division
vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
finder = new TGeoPatternZ(voldiv, ndiv, start, end);
voldiv->SetFinder(finder);
finder->SetDivIndex(voldiv->GetNdaughters());
for (id=0; id<ndiv; id++) {
Double_t z1 = start+id*step;
Double_t z2 = start+(id+1)*step;
Double_t rmin1n = 0.5*(fRmin1*(fDz-z1)+fRmin2*(fDz+z1))/fDz;
Double_t rmax1n = 0.5*(fRmax1*(fDz-z1)+fRmax2*(fDz+z1))/fDz;
Double_t rmin2n = 0.5*(fRmin1*(fDz-z2)+fRmin2*(fDz+z2))/fDz;
Double_t rmax2n = 0.5*(fRmax1*(fDz-z2)+fRmax2*(fDz+z2))/fDz;
shape = new TGeoCone(0.5*step,rmin1n, rmax1n, rmin2n, rmax2n);
vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
vmulti->AddVolume(vol);
opt = "Z";
voldiv->AddNodeOffset(vol, id, start+id*step+step/2, opt.Data());
((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);
}
return vmulti;
default:
Error("Divide", "Wrong axis type for division");
return 0;
}
}
//_____________________________________________________________________________
const char *TGeoCone::GetAxisName(Int_t iaxis) const
{
// Returns name of axis IAXIS.
switch (iaxis) {
case 1:
return "R";
case 2:
return "PHI";
case 3:
return "Z";
default:
return "undefined";
}
}
//_____________________________________________________________________________
Double_t TGeoCone::GetAxisRange(Int_t iaxis, Double_t &xlo, Double_t &xhi) const
{
// Get range of shape for a given axis.
xlo = 0;
xhi = 0;
Double_t dx = 0;
switch (iaxis) {
case 2:
xlo = 0.;
xhi = 360.;
return 360.;
case 3:
xlo = -fDz;
xhi = fDz;
dx = xhi-xlo;
return dx;
}
return dx;
}
//_____________________________________________________________________________
void TGeoCone::GetBoundingCylinder(Double_t *param) const
{
//--- Fill vector param[4] with the bounding cylinder parameters. The order
// is the following : Rmin, Rmax, Phi1, Phi2, dZ
param[0] = TMath::Min(fRmin1, fRmin2); // Rmin
param[0] *= param[0];
param[1] = TMath::Max(fRmax1, fRmax2); // Rmax
param[1] *= param[1];
param[2] = 0.; // Phi1
param[3] = 360.; // Phi1
}
//_____________________________________________________________________________
TGeoShape *TGeoCone::GetMakeRuntimeShape(TGeoShape *mother, TGeoMatrix * /*mat*/) const
{
// in case shape has some negative parameters, these has to be computed
// in order to fit the mother
if (!TestShapeBit(kGeoRunTimeShape)) return 0;
if (!mother->TestShapeBit(kGeoCone)) {
Error("GetMakeRuntimeShape", "invalid mother");
return 0;
}
Double_t rmin1, rmax1, rmin2, rmax2, dz;
rmin1 = fRmin1;
rmax1 = fRmax1;
rmin2 = fRmin2;
rmax2 = fRmax2;
dz = fDz;
if (fDz<0) dz=((TGeoCone*)mother)->GetDz();
if (fRmin1<0)
rmin1 = ((TGeoCone*)mother)->GetRmin1();
if (fRmax1<0)
rmax1 = ((TGeoCone*)mother)->GetRmax1();
if (fRmin2<0)
rmin2 = ((TGeoCone*)mother)->GetRmin2();
if (fRmax2<0)
rmax2 = ((TGeoCone*)mother)->GetRmax2();
return (new TGeoCone(GetName(), dz, rmin1, rmax1, rmin2, rmax2));
}
//_____________________________________________________________________________
void TGeoCone::InspectShape() const
{
// print shape parameters
printf("*** Shape %s TGeoCone ***\n", GetName());
printf(" dz =: %11.5f\n", fDz);
printf(" Rmin1 = %11.5f\n", fRmin1);
printf(" Rmax1 = %11.5f\n", fRmax1);
printf(" Rmin2 = %11.5f\n", fRmin2);
printf(" Rmax2 = %11.5f\n", fRmax2);
printf(" Bounding box:\n");
TGeoBBox::InspectShape();
}
//_____________________________________________________________________________
TBuffer3D *TGeoCone::MakeBuffer3D() const
{
// Creates a TBuffer3D describing *this* shape.
// Coordinates are in local reference frame.
Int_t n = gGeoManager->GetNsegments();
Int_t nbPnts = 4*n;
Int_t nbSegs = 8*n;
Int_t nbPols = 4*n;
TBuffer3D* buff = new TBuffer3D(TBuffer3DTypes::kGeneric,
nbPnts, 3*nbPnts,
nbSegs, 3*nbSegs,
nbPols, 6*nbPols);
if (buff)
{
SetPoints(buff->fPnts);
SetSegsAndPols(*buff);
}
return buff;
}
//_____________________________________________________________________________
void TGeoCone::SetSegsAndPols(TBuffer3D &buffer) const
{
// Fill TBuffer3D structure for segments and polygons.
Int_t i,j;
Int_t n = gGeoManager->GetNsegments();
Int_t c = GetBasicColor();
for (i = 0; i < 4; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c;
buffer.fSegs[(i*n+j)*3+1] = i*n+j;
buffer.fSegs[(i*n+j)*3+2] = i*n+j+1;
}
buffer.fSegs[(i*n+j-1)*3+2] = i*n;
}
for (i = 4; i < 6; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c+1;
buffer.fSegs[(i*n+j)*3+1] = (i-4)*n+j;
buffer.fSegs[(i*n+j)*3+2] = (i-2)*n+j;
}
}
for (i = 6; i < 8; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c;
buffer.fSegs[(i*n+j)*3+1] = 2*(i-6)*n+j;
buffer.fSegs[(i*n+j)*3+2] = (2*(i-6)+1)*n+j;
}
}
Int_t indx = 0;
i=0;
for (j = 0; j < n; j++) {
indx = 6*(i*n+j);
buffer.fPols[indx ] = c;
buffer.fPols[indx+1] = 4;
buffer.fPols[indx+5] = i*n+j;
buffer.fPols[indx+4] = (4+i)*n+j;
buffer.fPols[indx+3] = (2+i)*n+j;
buffer.fPols[indx+2] = (4+i)*n+j+1;
}
buffer.fPols[indx+2] = (4+i)*n;
i=1;
for (j = 0; j < n; j++) {
indx = 6*(i*n+j);
buffer.fPols[indx ] = c;
buffer.fPols[indx+1] = 4;
buffer.fPols[indx+2] = i*n+j;
buffer.fPols[indx+3] = (4+i)*n+j;
buffer.fPols[indx+4] = (2+i)*n+j;
buffer.fPols[indx+5] = (4+i)*n+j+1;
}
buffer.fPols[indx+5] = (4+i)*n;
i=2;
for (j = 0; j < n; j++) {
indx = 6*(i*n+j);
buffer.fPols[indx ] = c+i;
buffer.fPols[indx+1] = 4;
buffer.fPols[indx+2] = (i-2)*2*n+j;
buffer.fPols[indx+3] = (4+i)*n+j;
buffer.fPols[indx+4] = ((i-2)*2+1)*n+j;
buffer.fPols[indx+5] = (4+i)*n+j+1;
}
buffer.fPols[indx+5] = (4+i)*n;
i=3;
for (j = 0; j < n; j++) {
indx = 6*(i*n+j);
buffer.fPols[indx ] = c+i;
buffer.fPols[indx+1] = 4;
buffer.fPols[indx+5] = (i-2)*2*n+j;
buffer.fPols[indx+4] = (4+i)*n+j;
buffer.fPols[indx+3] = ((i-2)*2+1)*n+j;
buffer.fPols[indx+2] = (4+i)*n+j+1;
}
buffer.fPols[indx+2] = (4+i)*n;
}
//_____________________________________________________________________________
Double_t TGeoCone::Safety(Double_t *point, Bool_t in) const
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
Double_t saf[3];
Double_t ro1 = 0.5*(fRmin1+fRmin2);
Double_t tg1 = 0.5*(fRmin2-fRmin1)/fDz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(fRmax1+fRmax2);
Double_t tg2 = 0.5*(fRmax2-fRmax1)/fDz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
saf[0] = fDz-TMath::Abs(point[2]);
saf[1] = (ro1>0)?((r-rin)*cr1):TGeoShape::Big();
saf[2] = (rout-r)*cr2;
if (in) return saf[TMath::LocMin(3,saf)];
for (Int_t i=0; i<3; i++) saf[i]=-saf[i];
return saf[TMath::LocMax(3,saf)];
}
//_____________________________________________________________________________
Double_t TGeoCone::SafetyS(Double_t *point, Bool_t in, Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Int_t skipz)
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
Double_t saf[3];
Double_t ro1 = 0.5*(rmin1+rmin2);
Double_t tg1 = 0.5*(rmin2-rmin1)/dz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(rmax1+rmax2);
Double_t tg2 = 0.5*(rmax2-rmax1)/dz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
switch (skipz) {
case 1: // skip lower Z plane
saf[0] = dz - point[2];
break;
case 2: // skip upper Z plane
saf[0] = dz + point[2];
break;
case 3: // skip both
saf[0] = TGeoShape::Big();
break;
default:
saf[0] = dz-TMath::Abs(point[2]);
}
saf[1] = (ro1>0)?((r-rin)*cr1):TGeoShape::Big();
saf[2] = (rout-r)*cr2;
if (in) return saf[TMath::LocMin(3,saf)];
for (Int_t i=0; i<3; i++) saf[i]=-saf[i];
return saf[TMath::LocMax(3,saf)];
}
//_____________________________________________________________________________
void TGeoCone::SavePrimitive(ofstream &out, Option_t * /*option*/)
{
// Save a primitive as a C++ statement(s) on output stream "out".
if (TObject::TestBit(kGeoSavePrimitive)) return;
out << " // Shape: " << GetName() << " type: " << ClassName() << endl;
out << " dz = " << fDz << ";" << endl;
out << " rmin1 = " << fRmin1 << ";" << endl;
out << " rmax1 = " << fRmax1 << ";" << endl;
out << " rmin2 = " << fRmin2 << ";" << endl;
out << " rmax2 = " << fRmax2 << ";" << endl;
out << " TGeoShape *" << GetPointerName() << " = new TGeoCone(\"" << GetName() << "\", dz,rmin1,rmax1,rmin2,rmax2);" << endl;
TObject::SetBit(TGeoShape::kGeoSavePrimitive);
}
//_____________________________________________________________________________
void TGeoCone::SetConeDimensions(Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2)
{
if (rmin1>=0) {
if (rmax1>0) {
if (rmin1<=rmax1) {
// normal rmin/rmax
fRmin1 = rmin1;
fRmax1 = rmax1;
} else {
fRmin1 = rmax1;
fRmax1 = rmin1;
Warning("SetConeDimensions", "rmin1>rmax1 Switch rmin1<->rmax1");
SetShapeBit(TGeoShape::kGeoBad);
}
} else {
// run-time
fRmin1 = rmin1;
fRmax1 = rmax1;
}
} else {
// run-time
fRmin1 = rmin1;
fRmax1 = rmax1;
}
if (rmin2>=0) {
if (rmax2>0) {
if (rmin2<=rmax2) {
// normal rmin/rmax
fRmin2 = rmin2;
fRmax2 = rmax2;
} else {
fRmin2 = rmax2;
fRmax2 = rmin2;
Warning("SetConeDimensions", "rmin2>rmax2 Switch rmin2<->rmax2");
SetShapeBit(TGeoShape::kGeoBad);
}
} else {
// run-time
fRmin2 = rmin2;
fRmax2 = rmax2;
}
} else {
// run-time
fRmin2 = rmin2;
fRmax2 = rmax2;
}
fDz = dz;
}
//_____________________________________________________________________________
void TGeoCone::SetDimensions(Double_t *param)
{
Double_t dz = param[0];
Double_t rmin1 = param[1];
Double_t rmax1 = param[2];
Double_t rmin2 = param[3];
Double_t rmax2 = param[4];
SetConeDimensions(dz, rmin1, rmax1, rmin2, rmax2);
}
//_____________________________________________________________________________
void TGeoCone::SetPoints(Double_t *points) const
{
// create cone mesh points
Double_t dz, phi, dphi;
Int_t j, n;
n = gGeoManager->GetNsegments();
dphi = 360./n;
dz = fDz;
Int_t indx = 0;
if (points) {
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmin1 * TMath::Cos(phi);
points[indx++] = fRmin1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmax1 * TMath::Cos(phi);
points[indx++] = fRmax1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmin2 * TMath::Cos(phi);
points[indx++] = fRmin2 * TMath::Sin(phi);
points[indx++] = dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmax2 * TMath::Cos(phi);
points[indx++] = fRmax2 * TMath::Sin(phi);
points[indx++] = dz;
}
}
}
//_____________________________________________________________________________
void TGeoCone::SetPoints(Float_t *points) const
{
// create cone mesh points
Double_t dz, phi, dphi;
Int_t j, n;
n = gGeoManager->GetNsegments();
dphi = 360./n;
dz = fDz;
Int_t indx = 0;
if (points) {
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmin1 * TMath::Cos(phi);
points[indx++] = fRmin1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmax1 * TMath::Cos(phi);
points[indx++] = fRmax1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmin2 * TMath::Cos(phi);
points[indx++] = fRmin2 * TMath::Sin(phi);
points[indx++] = dz;
}
for (j = 0; j < n; j++) {
phi = j*dphi*TMath::DegToRad();
points[indx++] = fRmax2 * TMath::Cos(phi);
points[indx++] = fRmax2 * TMath::Sin(phi);
points[indx++] = dz;
}
}
}
//_____________________________________________________________________________
Int_t TGeoCone::GetNmeshVertices() const
{
// Return number of vertices of the mesh representation
Int_t n = gGeoManager->GetNsegments();
Int_t numPoints = n*4;
return numPoints;
}
//_____________________________________________________________________________
void TGeoCone::Sizeof3D() const
{
///// fill size of this 3-D object
/// TVirtualGeoPainter *painter = gGeoManager->GetGeomPainter();
/// if (!painter) return;
/// Int_t n = gGeoManager->GetNsegments();
/// Int_t numPoints = n*4;
/// Int_t numSegs = n*8;
/// Int_t numPolys = n*4;
/// painter->AddSize3D(numPoints, numSegs, numPolys);
}
//_____________________________________________________________________________
const TBuffer3D & TGeoCone::GetBuffer3D(Int_t reqSections, Bool_t localFrame) const
{
static TBuffer3D buffer(TBuffer3DTypes::kGeneric);
TGeoBBox::FillBuffer3D(buffer, reqSections, localFrame);
if (reqSections & TBuffer3D::kRawSizes) {
Int_t n = gGeoManager->GetNsegments();
Int_t nbPnts = 4*n;
Int_t nbSegs = 8*n;
Int_t nbPols = 4*n;
if (buffer.SetRawSizes(nbPnts, 3*nbPnts, nbSegs, 3*nbSegs, nbPols, 6*nbPols)) {
buffer.SetSectionsValid(TBuffer3D::kRawSizes);
}
}
// TODO: Can we push this as common down to TGeoShape?
if ((reqSections & TBuffer3D::kRaw) && buffer.SectionsValid(TBuffer3D::kRawSizes)) {
SetPoints(buffer.fPnts);
if (!buffer.fLocalFrame) {
TransformPoints(buffer.fPnts, buffer.NbPnts());
}
SetSegsAndPols(buffer);
buffer.SetSectionsValid(TBuffer3D::kRaw);
}
return buffer;
}
ClassImp(TGeoConeSeg)
//_____________________________________________________________________________
TGeoConeSeg::TGeoConeSeg()
{
// Default constructor
SetShapeBit(TGeoShape::kGeoConeSeg);
fPhi1 = fPhi2 = 0.0;
}
//_____________________________________________________________________________
TGeoConeSeg::TGeoConeSeg(Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Double_t phi1, Double_t phi2)
:TGeoCone(dz, rmin1, rmax1, rmin2, rmax2)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoConeSeg);
SetConsDimensions(dz, rmin1, rmax1, rmin2, rmax2, phi1, phi2);
ComputeBBox();
}
//_____________________________________________________________________________
TGeoConeSeg::TGeoConeSeg(const char *name, Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Double_t phi1, Double_t phi2)
:TGeoCone(name, dz, rmin1, rmax1, rmin2, rmax2)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoConeSeg);
SetConsDimensions(dz, rmin1, rmax1, rmin2, rmax2, phi1, phi2);
ComputeBBox();
}
//_____________________________________________________________________________
TGeoConeSeg::TGeoConeSeg(Double_t *param)
:TGeoCone(0,0,0,0,0)
{
// Default constructor specifying minimum and maximum radius
// param[0] = dz
// param[1] = Rmin1
// param[2] = Rmax1
// param[3] = Rmin2
// param[4] = Rmax2
// param[5] = phi1
// param[6] = phi2
SetShapeBit(TGeoShape::kGeoConeSeg);
SetDimensions(param);
ComputeBBox();
}
//_____________________________________________________________________________
TGeoConeSeg::~TGeoConeSeg()
{
// destructor
}
//_____________________________________________________________________________
void TGeoConeSeg::ComputeBBox()
{
// compute bounding box of the tube segment
Double_t rmin, rmax;
rmin = TMath::Min(fRmin1, fRmin2);
rmax = TMath::Max(fRmax1, fRmax2);
Double_t xc[4];
Double_t yc[4];
xc[0] = rmax*TMath::Cos(fPhi1*TMath::DegToRad());
yc[0] = rmax*TMath::Sin(fPhi1*TMath::DegToRad());
xc[1] = rmax*TMath::Cos(fPhi2*TMath::DegToRad());
yc[1] = rmax*TMath::Sin(fPhi2*TMath::DegToRad());
xc[2] = rmin*TMath::Cos(fPhi1*TMath::DegToRad());
yc[2] = rmin*TMath::Sin(fPhi1*TMath::DegToRad());
xc[3] = rmin*TMath::Cos(fPhi2*TMath::DegToRad());
yc[3] = rmin*TMath::Sin(fPhi2*TMath::DegToRad());
Double_t xmin = xc[TMath::LocMin(4, &xc[0])];
Double_t xmax = xc[TMath::LocMax(4, &xc[0])];
Double_t ymin = yc[TMath::LocMin(4, &yc[0])];
Double_t ymax = yc[TMath::LocMax(4, &yc[0])];
Double_t dp = fPhi2-fPhi1;
Double_t ddp = -fPhi1;
if (ddp<0) ddp+= 360;
if (ddp<=dp) xmax = rmax;
ddp = 90-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp<=dp) ymax = rmax;
ddp = 180-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp<=dp) xmin = -rmax;
ddp = 270-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp<=dp) ymin = -rmax;
fOrigin[0] = (xmax+xmin)/2;
fOrigin[1] = (ymax+ymin)/2;
fOrigin[2] = 0;
fDX = (xmax-xmin)/2;
fDY = (ymax-ymin)/2;
fDZ = fDz;
}
//_____________________________________________________________________________
void TGeoConeSeg::ComputeNormal(Double_t *point, Double_t *dir, Double_t *norm)
{
// Compute normal to closest surface from POINT.
Double_t saf[3];
Double_t ro1 = 0.5*(fRmin1+fRmin2);
Double_t tg1 = 0.5*(fRmin2-fRmin1)/fDz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(fRmax1+fRmax2);
Double_t tg2 = 0.5*(fRmax2-fRmax1)/fDz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t c1 = TMath::Cos(fPhi1*TMath::DegToRad());
Double_t s1 = TMath::Sin(fPhi1*TMath::DegToRad());
Double_t c2 = TMath::Cos(fPhi2*TMath::DegToRad());
Double_t s2 = TMath::Sin(fPhi2*TMath::DegToRad());
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
saf[0] = TMath::Abs(fDz-TMath::Abs(point[2]));
saf[1] = (ro1>0)?(TMath::Abs((r-rin)*cr1)):TGeoShape::Big();
saf[2] = TMath::Abs((rout-r)*cr2);
Int_t i = TMath::LocMin(3,saf);
if (TGeoShape::IsCloseToPhi(saf[i], point,c1,s1,c2,s2)) {
TGeoShape::NormalPhi(point,dir,norm,c1,s1,c2,s2);
return;
}
if (i==0) {
norm[0] = norm[1] = 0.;
norm[2] = TMath::Sign(1.,dir[2]);
return;
}
Double_t phi = TMath::ATan2(point[1],point[0]);
Double_t cphi = TMath::Cos(phi);
Double_t sphi = TMath::Sin(phi);
if (i==1) {
norm[0] = cr1*cphi;
norm[1] = cr1*sphi;
norm[2] = -tg1*cr1;
} else {
norm[0] = cr2*cphi;
norm[1] = cr2*sphi;
norm[2] = -tg2*cr2;
}
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
void TGeoConeSeg::ComputeNormalS(Double_t *point, Double_t *dir, Double_t *norm,
Double_t dz, Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2,
Double_t c1, Double_t s1, Double_t c2, Double_t s2)
{
// Compute normal to closest surface from POINT.
Double_t saf[2];
Double_t ro1 = 0.5*(rmin1+rmin2);
Double_t tg1 = 0.5*(rmin2-rmin1)/dz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(rmax1+rmax2);
Double_t tg2 = 0.5*(rmax2-rmax1)/dz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
saf[0] = (ro1>0)?(TMath::Abs((r-rin)*cr1)):TGeoShape::Big();
saf[1] = TMath::Abs((rout-r)*cr2);
Int_t i = TMath::LocMin(2,saf);
if (TGeoShape::IsCloseToPhi(saf[i], point,c1,s1,c2,s2)) {
TGeoShape::NormalPhi(point,dir,norm,c1,s1,c2,s2);
return;
}
Double_t phi = TMath::ATan2(point[1],point[0]);
Double_t cphi = TMath::Cos(phi);
Double_t sphi = TMath::Sin(phi);
if (i==0) {
norm[0] = cr1*cphi;
norm[1] = cr1*sphi;
norm[2] = -tg1*cr1;
} else {
norm[0] = cr2*cphi;
norm[1] = cr2*sphi;
norm[2] = -tg2*cr2;
}
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
Bool_t TGeoConeSeg::Contains(Double_t *point) const
{
// test if point is inside this sphere
if (!TGeoCone::Contains(point)) return kFALSE;
Double_t phi = TMath::ATan2(point[1], point[0]) * TMath::RadToDeg();
if (phi < 0 ) phi+=360.;
Double_t dphi = fPhi2 - fPhi1;
Double_t ddp = phi-fPhi1;
if (ddp < 0) ddp+=360.;
// if (ddp > 360) ddp-=360;
if (ddp > dphi) return kFALSE;
return kTRUE;
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistToCons(Double_t *point, Double_t *dir, Double_t r1, Double_t z1, Double_t r2, Double_t z2, Double_t phi1, Double_t phi2)
{
// Static method to compute distance to a conical surface with :
// - r1, z1 - radius and Z position of lower base
// - r2, z2 - radius and Z position of upper base
// - phi1, phi2 - phi limits
Double_t dz = z2-z1;
if (dz<=0) {
return TGeoShape::Big();
}
Double_t dphi = phi2 - phi1;
if (dphi < 0) dphi+=360.;
// printf("phi1=%f phi2=%f dphi=%f\n", phi1, phi2, dphi);
Double_t ro0 = 0.5*(r1+r2);
Double_t fz = (r2-r1)/dz;
Double_t r0sq = point[0]*point[0] + point[1]*point[1];
Double_t rc = ro0 + fz*(point[2]-0.5*(z1+z2));
Double_t a = dir[0]*dir[0] + dir[1]*dir[1] - fz*fz*dir[2]*dir[2];
Double_t b = point[0]*dir[0] + point[1]*dir[1] - fz*rc*dir[2];
Double_t c = r0sq - rc*rc;
if (a==0) return TGeoShape::Big();
a = 1./a;
b *= a;
c *= a;
Double_t delta = b*b - c;
if (delta<0) return TGeoShape::Big();
delta = TMath::Sqrt(delta);
Double_t snxt = -b-delta;
Double_t ptnew[3];
Double_t ddp, phi;
if (snxt>0) {
// check Z range
ptnew[2] = point[2] + snxt*dir[2];
if (((ptnew[2]-z1)*(ptnew[2]-z2)) < 0) {
// check phi range
ptnew[0] = point[0] + snxt*dir[0];
ptnew[1] = point[1] + snxt*dir[1];
phi = TMath::ATan2(ptnew[1], ptnew[0]) * TMath::RadToDeg();
if (phi < 0 ) phi+=360.;
ddp = phi-phi1;
if (ddp < 0) ddp+=360.;
// printf("snxt1=%f phi=%f ddp=%f\n", snxt, phi, ddp);
if (ddp<=dphi) return snxt;
}
}
snxt = -b+delta;
if (snxt>0) {
// check Z range
ptnew[2] = point[2] + snxt*dir[2];
if (((ptnew[2]-z1)*(ptnew[2]-z2)) < 0) {
// check phi range
ptnew[0] = point[0] + snxt*dir[0];
ptnew[1] = point[1] + snxt*dir[1];
phi = TMath::ATan2(ptnew[1], ptnew[0]) * TMath::RadToDeg();
if (phi < 0 ) phi+=360.;
ddp = phi-phi1;
if (ddp < 0) ddp+=360.;
// printf("snxt2=%f phi=%f ddp=%f\n", snxt, phi, ddp);
if (ddp<=dphi) return snxt;
}
}
return TGeoShape::Big();
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistFromInsideS(Double_t *point, Double_t *dir, Double_t dz,
Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2,
Double_t c1, Double_t s1, Double_t c2, Double_t s2, Double_t cm, Double_t sm, Double_t cdfi)
{
// compute distance from inside point to surface of the tube segment
if (dz<=0) return TGeoShape::Big();
// Do Z
Double_t scone = TGeoCone::DistFromInsideS(point,dir,dz,rmin1,rmax1,rmin2,rmax2);
if (scone<=0) return 0.0;
Double_t sfmin = TGeoShape::Big();
Double_t rsq = point[0]*point[0]+point[1]*point[1];
Double_t r = TMath::Sqrt(rsq);
Double_t cpsi=point[0]*cm+point[1]*sm;
if (cpsi>r*cdfi+TGeoShape::Tolerance()) {
sfmin = TGeoShape::DistToPhiMin(point, dir, s1, c1, s2, c2, sm, cm);
return TMath::Min(scone,sfmin);
}
// Point on the phi boundary or outside
// which one: phi1 or phi2
Double_t ddotn, xi, yi;
if (TMath::Abs(point[1]-s1*r) < TMath::Abs(point[1]-s2*r)) {
ddotn = s1*dir[0]-c1*dir[1];
if (ddotn>=0) return 0.0;
ddotn = -s2*dir[0]+c2*dir[1];
if (ddotn<=0) return scone;
sfmin = s2*point[0]-c2*point[1];
if (sfmin<=0) return scone;
sfmin /= ddotn;
if (sfmin >= scone) return scone;
xi = point[0]+sfmin*dir[0];
yi = point[1]+sfmin*dir[1];
if (yi*cm-xi*sm<0) return scone;
return sfmin;
}
ddotn = -s2*dir[0]+c2*dir[1];
if (ddotn>=0) return 0.0;
ddotn = s1*dir[0]-c1*dir[1];
if (ddotn<=0) return scone;
sfmin = -s1*point[0]+c1*point[1];
if (sfmin<=0) return scone;
sfmin /= ddotn;
if (sfmin >= scone) return scone;
xi = point[0]+sfmin*dir[0];
yi = point[1]+sfmin*dir[1];
if (yi*cm-xi*sm>0) return scone;
return sfmin;
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistFromInside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from inside point to surface of the tube segment
if (iact<3 && safe) {
*safe = TGeoConeSeg::SafetyS(point, kTRUE, fDz,fRmin1,fRmax1,fRmin2,fRmax2,fPhi1,fPhi2);
if (iact==0) return TGeoShape::Big();
if ((iact==1) && (*safe>step)) return TGeoShape::Big();
}
Double_t phi1 = fPhi1*TMath::DegToRad();
Double_t phi2 = fPhi2*TMath::DegToRad();
Double_t c1 = TMath::Cos(phi1);
Double_t c2 = TMath::Cos(phi2);
Double_t s1 = TMath::Sin(phi1);
Double_t s2 = TMath::Sin(phi2);
Double_t phim = 0.5*(phi1+phi2);
Double_t cm = TMath::Cos(phim);
Double_t sm = TMath::Sin(phim);
Double_t dfi = 0.5*(phi2-phi1);
Double_t cdfi = TMath::Cos(dfi);
// compute distance to surface
return TGeoConeSeg::DistFromInsideS(point,dir,fDz,fRmin1,fRmax1,fRmin2,fRmax2,c1,s1,c2,s2,cm,sm,cdfi);
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistFromOutsideS(Double_t *point, Double_t *dir, Double_t dz,
Double_t rmin1, Double_t rmax1, Double_t rmin2, Double_t rmax2,
Double_t c1, Double_t s1, Double_t c2, Double_t s2, Double_t cm, Double_t sm, Double_t cdfi)
{
// compute distance from outside point to surface of arbitrary tube
if (dz<=0) return TGeoShape::Big();
Double_t r2, cpsi;
// check Z planes
Double_t xi, yi, zi;
Double_t b,delta;
zi = dz - TMath::Abs(point[2]);
Double_t rin,rout;
Double_t s = TGeoShape::Big();
Double_t snxt=TGeoShape::Big();
Bool_t in = kFALSE;
Bool_t inz = (zi<0)?kFALSE:kTRUE;
if (!inz) {
if (point[2]*dir[2]>=0) return TGeoShape::Big();
s = -zi/TMath::Abs(dir[2]);
xi = point[0]+s*dir[0];
yi = point[1]+s*dir[1];
r2=xi*xi+yi*yi;
if (dir[2]>0) {
rin = rmin1;
rout = rmax1;
} else {
rin = rmin2;
rout = rmax2;
}
if ((rin*rin<=r2) && (r2<=rout*rout)) {
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) return s;
}
}
Double_t zinv = 1./dz;
Double_t rsq = point[0]*point[0]+point[1]*point[1];
Double_t r = TMath::Sqrt(rsq);
Double_t ro1=0.5*(rmin1+rmin2);
Bool_t hasrmin = (ro1>0)?kTRUE:kFALSE;
Double_t tg1 = 0.0;
Bool_t inrmin = kFALSE;
rin = 0.0;
if (hasrmin) {
tg1=0.5*(rmin2-rmin1)*zinv;
rin = ro1+tg1*point[2];
if (rsq > rin*(rin-TGeoShape::Tolerance())) inrmin=kTRUE;
} else {
inrmin = kTRUE;
}
Double_t ro2=0.5*(rmax1+rmax2);
Double_t tg2=0.5*(rmax2-rmax1)*zinv;
rout = ro2+tg2*point[2];
Bool_t inrmax = kFALSE;
if (rsq < rout*(rout+TGeoShape::Tolerance())) inrmax = kTRUE;
Bool_t inphi = kFALSE;
cpsi=point[0]*cm+point[1]*sm;
if (cpsi>r*cdfi-TGeoShape::Tolerance()) inphi = kTRUE;
in = inz & inrmin & inrmax & inphi;
// If inside, we are most likely on a boundary within machine precision.
if (in) {
Double_t safphi = (cpsi-r*cdfi)*TMath::Sqrt(1.-cdfi*cdfi);
Double_t safrmin = (hasrmin)?TMath::Abs(r-rin):(TGeoShape::Big());
Double_t safrmax = TMath::Abs(r-rout);
// check if on Z boundaries
if (zi<safrmax && zi<safrmin && zi<safphi) {
if (point[2]*dir[2]<0) return 0.0;
return TGeoShape::Big();
}
// check if on Rmax boundary
if (safrmax<safrmin && safrmax<safphi) {
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg2*dir[2]*r;
if (ddotn<=0) return 0.0;
return TGeoShape::Big();
}
// check if on phi boundary
if (safphi<safrmin) {
// We may cross again a phi of rmin boundary
// check first if we are on phi1 or phi2
Double_t un;
if (TMath::Abs(point[1]-s1*r) < TMath::Abs(point[1]-s2*r)) {
un = dir[0]*s1-dir[1]*c1;
if (un < 0) return 0.0;
if (cdfi>=0) return TGeoShape::Big();
un = -dir[0]*s2+dir[1]*c2;
if (un<0) {
s = -point[0]*s2+point[1]*c2;
if (s>0) {
s /= (-un);
zi = point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi = point[0]+s*dir[0];
yi = point[1]+s*dir[1];
if ((yi*cm-xi*sm)>0) {
r2=xi*xi+yi*yi;
rin = ro1+tg1*zi;
rout = ro2+tg2*zi;
if ((rin*rin<=r2) && (rout*rout>=r2)) return s;
}
}
}
}
} else {
un = -dir[0]*s2+dir[1]*c2;
if (un < 0) return 0.0;
if (cdfi>=0) return TGeoShape::Big();
un = dir[0]*s1-dir[1]*c1;
if (un<0) {
s = point[0]*s1-point[1]*c1;
if (s>0) {
s /= (-un);
zi = point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi = point[0]+s*dir[0];
yi = point[1]+s*dir[1];
if ((yi*cm-xi*sm)<0) {
r2=xi*xi+yi*yi;
rin = ro1+tg1*zi;
rout = ro2+tg2*zi;
if ((rin*rin<=r2) && (rout*rout>=r2)) return s;
}
}
}
}
}
// We may also cross rmin, second solution coming from outside
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg1*dir[2]*r;
if (ddotn>=0) return TGeoShape::Big();
if (cdfi>=0) return TGeoShape::Big();
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta<0) return TGeoShape::Big();
snxt = -b-delta;
if (snxt<0) return TGeoShape::Big();
snxt = -b+delta;
zi = point[2]+snxt*dir[2];
if (TMath::Abs(zi)>dz) return TGeoShape::Big();
xi = point[0]+snxt*dir[0];
yi = point[1]+snxt*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) return snxt;
return TGeoShape::Big();
}
// We are on rmin boundary: we may cross again rmin or a phi facette
Double_t ddotn = point[0]*dir[0]+point[1]*dir[1]-tg1*dir[2]*r;
if (ddotn>=0) return 0.0;
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta<0) return 0.0;
snxt = -b+delta;
if (snxt<0) return TGeoShape::Big();
if (TMath::Abs(-b-delta)>snxt) return TGeoShape::Big();
zi = point[2]+snxt*dir[2];
if (TMath::Abs(zi)>dz) return TGeoShape::Big();
// OK, we cross rmin at snxt - check if within phi range
xi = point[0]+snxt*dir[0];
yi = point[1]+snxt*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) return snxt;
// we cross rmin in the phi gap - we may cross a phi facette
if (cdfi>=0) return TGeoShape::Big();
Double_t un=-dir[0]*s1+dir[1]*c1;
if (un > 0) {
s=point[0]*s1-point[1]*c1;
if (s>=0) {
s /= un;
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
if ((yi*cm-xi*sm)<=0) {
r2=xi*xi+yi*yi;
rin = ro1+tg1*zi;
rout = ro2+tg2*zi;
if ((rin*rin<=r2) && (rout*rout>=r2)) return s;
}
}
}
}
un=dir[0]*s2-dir[1]*c2;
if (un > 0) {
s=(point[1]*c2-point[0]*s2)/un;
if (s>=0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
if ((yi*cm-xi*sm)>=0) {
r2=xi*xi+yi*yi;
rin = ro1+tg1*zi;
rout = ro2+tg2*zi;
if ((rin*rin<=r2) && (rout*rout>=r2)) return s;
}
}
}
}
return TGeoShape::Big();
}
// The point is really outside
Double_t sr1 = TGeoShape::Big();
if (!inrmax) {
// check crossing with outer cone
TGeoCone::DistToCone(point, dir, dz, rmax1, rmax2, b, delta);
if (delta>=0) {
s = -b-delta;
if (s>0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) return s; // rmax crossing
}
}
s = -b+delta;
if (s>0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) sr1=s;
}
}
}
}
// check crossing with inner cone
Double_t sr2 = TGeoShape::Big();
TGeoCone::DistToCone(point, dir, dz, rmin1, rmin2, b, delta);
if (delta>=0) {
s = -b-delta;
if (s>0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) sr2=s;
}
}
if (sr2>1E10) {
s = -b+delta;
if (s>0) {
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)<=dz) {
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
cpsi=xi*cm+yi*sm;
if (cpsi>=(cdfi*TMath::Sqrt(r2))) sr2=s;
}
}
}
}
snxt = TMath::Min(sr1,sr2);
// Check phi crossing
s = TGeoShape::DistToPhiMin(point,dir,s1,c1,s2,c2,sm,cm,kFALSE);
if (s>snxt) return snxt;
zi=point[2]+s*dir[2];
if (TMath::Abs(zi)>dz) return snxt;
xi=point[0]+s*dir[0];
yi=point[1]+s*dir[1];
r2=xi*xi+yi*yi;
rout = ro2+tg2*zi;
if (r2>rout*rout) return snxt;
rin = ro1+tg1*zi;
if (r2>=rin*rin) return s; // phi crossing
return snxt;
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::DistFromOutside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from outside point to surface of the tube
// compute safe radius
if (iact<3 && safe) {
*safe = Safety(point, kFALSE);
if (iact==0) return TGeoShape::Big();
if ((iact==1) && (*safe>step)) return TGeoShape::Big();
}
Double_t phi1 = fPhi1*TMath::DegToRad();
Double_t phi2 = fPhi2*TMath::DegToRad();
Double_t c1 = TMath::Cos(phi1);
Double_t c2 = TMath::Cos(phi2);
Double_t s1 = TMath::Sin(phi1);
Double_t s2 = TMath::Sin(phi2);
Double_t phim = 0.5*(phi1+phi2);
Double_t cm = TMath::Cos(phim);
Double_t sm = TMath::Sin(phim);
Double_t dfi = 0.5*(phi2-phi1);
Double_t cdfi = TMath::Cos(dfi);
return TGeoConeSeg::DistFromOutsideS(point,dir,fDz,fRmin1,fRmax1,fRmin2,fRmax2,c1,s1,c2,s2,cm,sm,cdfi);
}
//_____________________________________________________________________________
Int_t TGeoConeSeg::DistancetoPrimitive(Int_t px, Int_t py)
{
// compute closest distance from point px,py to each corner
Int_t n = gGeoManager->GetNsegments()+1;
const Int_t numPoints = 4*n;
return ShapeDistancetoPrimitive(numPoints, px, py);
}
//_____________________________________________________________________________
TGeoVolume *TGeoConeSeg::Divide(TGeoVolume *voldiv, const char *divname, Int_t iaxis, Int_t ndiv,
Double_t start, Double_t step)
{
//--- Divide this cone segment shape belonging to volume "voldiv" into ndiv volumes
// called divname, from start position with the given step. Returns pointer
// to created division cell volume in case of Z divisions. For Z division
// creates all volumes with different shapes and returns pointer to volume that
// was divided. In case a wrong division axis is supplied, returns pointer to
// volume that was divided.
TGeoShape *shape; //--- shape to be created
TGeoVolume *vol; //--- division volume to be created
TGeoVolumeMulti *vmulti; //--- generic divided volume
TGeoPatternFinder *finder; //--- finder to be attached
TString opt = ""; //--- option to be attached
Double_t dphi;
Int_t id;
Double_t end = start+ndiv*step;
switch (iaxis) {
case 1: //--- R division
Error("Divide","division of a cone segment on R not implemented");
return 0;
case 2: //--- Phi division
dphi = fPhi2-fPhi1;
if (dphi<0) dphi+=360.;
finder = new TGeoPatternCylPhi(voldiv, ndiv, start, end);
voldiv->SetFinder(finder);
finder->SetDivIndex(voldiv->GetNdaughters());
shape = new TGeoConeSeg(fDz, fRmin1, fRmax1, fRmin2, fRmax2, -step/2, step/2);
vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
vmulti->AddVolume(vol);
opt = "Phi";
for (id=0; id<ndiv; id++) {
voldiv->AddNodeOffset(vol, id, start+id*step+step/2, opt.Data());
((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);
}
return vmulti;
case 3: //--- Z division
finder = new TGeoPatternZ(voldiv, ndiv, start, end);
vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
voldiv->SetFinder(finder);
finder->SetDivIndex(voldiv->GetNdaughters());
for (id=0; id<ndiv; id++) {
Double_t z1 = start+id*step;
Double_t z2 = start+(id+1)*step;
Double_t rmin1n = 0.5*(fRmin1*(fDz-z1)+fRmin2*(fDz+z1))/fDz;
Double_t rmax1n = 0.5*(fRmax1*(fDz-z1)+fRmax2*(fDz+z1))/fDz;
Double_t rmin2n = 0.5*(fRmin1*(fDz-z2)+fRmin2*(fDz+z2))/fDz;
Double_t rmax2n = 0.5*(fRmax1*(fDz-z2)+fRmax2*(fDz+z2))/fDz;
shape = new TGeoConeSeg(step/2, rmin1n, rmax1n, rmin2n, rmax2n, fPhi1, fPhi2);
vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
vmulti->AddVolume(vol);
opt = "Z";
voldiv->AddNodeOffset(vol, id, start+id*step+step/2, opt.Data());
((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);
}
return vmulti;
default:
Error("Divide", "Wrong axis type for division");
return 0;
}
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::GetAxisRange(Int_t iaxis, Double_t &xlo, Double_t &xhi) const
{
// Get range of shape for a given axis.
xlo = 0;
xhi = 0;
Double_t dx = 0;
switch (iaxis) {
case 2:
xlo = fPhi1;
xhi = fPhi2;
dx = xhi-xlo;
return dx;
case 3:
xlo = -fDz;
xhi = fDz;
dx = xhi-xlo;
return dx;
}
return dx;
}
//_____________________________________________________________________________
void TGeoConeSeg::GetBoundingCylinder(Double_t *param) const
{
//--- Fill vector param[4] with the bounding cylinder parameters. The order
// is the following : Rmin, Rmax, Phi1, Phi2
param[0] = TMath::Min(fRmin1, fRmin2); // Rmin
param[0] *= param[0];
param[1] = TMath::Max(fRmax1, fRmax2); // Rmax
param[1] *= param[1];
param[2] = (fPhi1<0)?(fPhi1+360.):fPhi1; // Phi1
param[3] = fPhi2; // Phi2
while (param[3]<param[2]) param[3]+=360.;
}
//_____________________________________________________________________________
TGeoShape *TGeoConeSeg::GetMakeRuntimeShape(TGeoShape *mother, TGeoMatrix * /*mat*/) const
{
// in case shape has some negative parameters, these has to be computed
// in order to fit the mother
if (!TestShapeBit(kGeoRunTimeShape)) return 0;
if (!mother->TestShapeBit(kGeoConeSeg)) {
Error("GetMakeRuntimeShape", "invalid mother");
return 0;
}
Double_t rmin1, rmax1, rmin2, rmax2, dz;
rmin1 = fRmin1;
rmax1 = fRmax1;
rmin2 = fRmin2;
rmax2 = fRmax2;
dz = fDz;
if (fDz<0) dz=((TGeoCone*)mother)->GetDz();
if (fRmin1<0)
rmin1 = ((TGeoCone*)mother)->GetRmin1();
if ((fRmax1<0) || (fRmax1<fRmin1))
rmax1 = ((TGeoCone*)mother)->GetRmax1();
if (fRmin2<0)
rmin2 = ((TGeoCone*)mother)->GetRmin2();
if ((fRmax2<0) || (fRmax2<fRmin2))
rmax2 = ((TGeoCone*)mother)->GetRmax2();
return (new TGeoConeSeg(GetName(), dz, rmin1, rmax1, rmin2, rmax2, fPhi1, fPhi2));
}
//_____________________________________________________________________________
void TGeoConeSeg::InspectShape() const
{
// print shape parameters
printf("*** Shape %s: TGeoConeSeg ***\n", GetName());
printf(" dz = %11.5f\n", fDz);
printf(" Rmin1 = %11.5f\n", fRmin1);
printf(" Rmax1 = %11.5f\n", fRmax1);
printf(" Rmin2 = %11.5f\n", fRmin2);
printf(" Rmax2 = %11.5f\n", fRmax2);
printf(" phi1 = %11.5f\n", fPhi1);
printf(" phi2 = %11.5f\n", fPhi2);
printf(" Bounding box:\n");
TGeoBBox::InspectShape();
}
//_____________________________________________________________________________
TBuffer3D *TGeoConeSeg::MakeBuffer3D() const
{
// Creates a TBuffer3D describing *this* shape.
// Coordinates are in local reference frame.
Int_t n = gGeoManager->GetNsegments()+1;
Int_t nbPnts = 4*n;
Int_t nbSegs = 2*nbPnts;
Int_t nbPols = nbPnts-2;
TBuffer3D* buff = new TBuffer3D(TBuffer3DTypes::kGeneric,
nbPnts, 3*nbPnts,
nbSegs, 3*nbSegs,
nbPols, 6*nbPols);
if (buff)
{
SetPoints(buff->fPnts);
SetSegsAndPols(*buff);
}
return buff;
}
//_____________________________________________________________________________
void TGeoConeSeg::SetSegsAndPols(TBuffer3D &buffer) const
{
// Fill TBuffer3D structure for segments and polygons.
Int_t i, j;
Int_t n = gGeoManager->GetNsegments()+1;
Int_t c = GetBasicColor();
memset(buffer.fSegs, 0, buffer.NbSegs()*3*sizeof(Int_t));
for (i = 0; i < 4; i++) {
for (j = 1; j < n; j++) {
buffer.fSegs[(i*n+j-1)*3 ] = c;
buffer.fSegs[(i*n+j-1)*3+1] = i*n+j-1;
buffer.fSegs[(i*n+j-1)*3+2] = i*n+j;
}
}
for (i = 4; i < 6; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c+1;
buffer.fSegs[(i*n+j)*3+1] = (i-4)*n+j;
buffer.fSegs[(i*n+j)*3+2] = (i-2)*n+j;
}
}
for (i = 6; i < 8; i++) {
for (j = 0; j < n; j++) {
buffer.fSegs[(i*n+j)*3 ] = c;
buffer.fSegs[(i*n+j)*3+1] = 2*(i-6)*n+j;
buffer.fSegs[(i*n+j)*3+2] = (2*(i-6)+1)*n+j;
}
}
Int_t indx = 0;
memset(buffer.fPols, 0, buffer.NbPols()*6*sizeof(Int_t));
i = 0;
for (j = 0; j < n-1; j++) {
buffer.fPols[indx++] = c;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = (4+i)*n+j+1;
buffer.fPols[indx++] = (2+i)*n+j;
buffer.fPols[indx++] = (4+i)*n+j;
buffer.fPols[indx++] = i*n+j;
}
i = 1;
for (j = 0; j < n-1; j++) {
buffer.fPols[indx++] = c;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = i*n+j;
buffer.fPols[indx++] = (4+i)*n+j;
buffer.fPols[indx++] = (2+i)*n+j;
buffer.fPols[indx++] = (4+i)*n+j+1;
}
i = 2;
for (j = 0; j < n-1; j++) {
buffer.fPols[indx++] = c+i;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = (i-2)*2*n+j;
buffer.fPols[indx++] = (4+i)*n+j;
buffer.fPols[indx++] = ((i-2)*2+1)*n+j;
buffer.fPols[indx++] = (4+i)*n+j+1;
}
i = 3;
for (j = 0; j < n-1; j++) {
buffer.fPols[indx++] = c+i;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = (4+i)*n+j+1;
buffer.fPols[indx++] = ((i-2)*2+1)*n+j;
buffer.fPols[indx++] = (4+i)*n+j;
buffer.fPols[indx++] = (i-2)*2*n+j;
}
buffer.fPols[indx++] = c+2;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = 6*n;
buffer.fPols[indx++] = 4*n;
buffer.fPols[indx++] = 7*n;
buffer.fPols[indx++] = 5*n;
buffer.fPols[indx++] = c+2;
buffer.fPols[indx++] = 4;
buffer.fPols[indx++] = 6*n-1;
buffer.fPols[indx++] = 8*n-1;
buffer.fPols[indx++] = 5*n-1;
buffer.fPols[indx++] = 7*n-1;
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::Safety(Double_t *point, Bool_t in) const
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
Double_t saf[3];
Double_t ro1 = 0.5*(fRmin1+fRmin2);
Double_t tg1 = 0.5*(fRmin2-fRmin1)/fDz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(fRmax1+fRmax2);
Double_t tg2 = 0.5*(fRmax2-fRmax1)/fDz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
Double_t safe = TGeoShape::Big();
if (in) {
saf[0] = fDz-TMath::Abs(point[2]);
saf[1] = (r-rin)*cr1;
saf[2] = (rout-r)*cr2;
safe = saf[TMath::LocMin(3,saf)];
} else {
saf[0] = TMath::Abs(point[2])-fDz; // positive if inside
saf[1] = (rin-r)*cr1;
saf[2] = (r-rout)*cr2;
safe = saf[TMath::LocMax(3,saf)];
}
Double_t safphi = TGeoShape::SafetyPhi(point, in, fPhi1, fPhi2);
if (in) return TMath::Min(safe, safphi);
return TMath::Max(safe, safphi);
}
//_____________________________________________________________________________
Double_t TGeoConeSeg::SafetyS(Double_t *point, Bool_t in, Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Double_t phi1, Double_t phi2, Int_t skipz)
{
// Static method to compute the closest distance from given point to this shape.
Double_t saf[3];
Double_t ro1 = 0.5*(rmin1+rmin2);
Double_t tg1 = 0.5*(rmin2-rmin1)/dz;
Double_t cr1 = 1./TMath::Sqrt(1.+tg1*tg1);
Double_t ro2 = 0.5*(rmax1+rmax2);
Double_t tg2 = 0.5*(rmax2-rmax1)/dz;
Double_t cr2 = 1./TMath::Sqrt(1.+tg2*tg2);
Double_t r=TMath::Sqrt(point[0]*point[0]+point[1]*point[1]);
Double_t rin = tg1*point[2]+ro1;
Double_t rout = tg2*point[2]+ro2;
Double_t safe = TGeoShape::Big();
switch (skipz) {
case 1: // skip lower Z plane
saf[0] = dz - point[2];
break;
case 2: // skip upper Z plane
saf[0] = dz + point[2];
break;
case 3: // skip both
saf[0] = TGeoShape::Big();
default:
saf[0] = dz-TMath::Abs(point[2]);
}
saf[1] = (r-rin)*cr1;
saf[2] = (rout-r)*cr2;
Double_t safphi = TGeoShape::SafetyPhi(point,in,phi1,phi2);
if (in) {
safe = saf[TMath::LocMin(3,saf)];
return TMath::Min(safe,safphi);
}
for (Int_t i=0; i<3; i++) saf[i]=-saf[i];
safe = saf[TMath::LocMax(3,saf)];
return TMath::Max(safe,safphi);
}
//_____________________________________________________________________________
void TGeoConeSeg::SavePrimitive(ofstream &out, Option_t * /*option*/)
{
// Save a primitive as a C++ statement(s) on output stream "out".
if (TObject::TestBit(kGeoSavePrimitive)) return;
out << " // Shape: " << GetName() << " type: " << ClassName() << endl;
out << " dz = " << fDz << ";" << endl;
out << " rmin1 = " << fRmin1 << ";" << endl;
out << " rmax1 = " << fRmax1 << ";" << endl;
out << " rmin2 = " << fRmin2 << ";" << endl;
out << " rmax2 = " << fRmax2 << ";" << endl;
out << " phi1 = " << fPhi1 << ";" << endl;
out << " phi2 = " << fPhi2 << ";" << endl;
out << " TGeoShape *" << GetPointerName() << " = new TGeoConeSeg(\"" << GetName() << "\", dz,rmin1,rmax1,rmin2,rmax2,phi1,phi2);" << endl;
TObject::SetBit(TGeoShape::kGeoSavePrimitive);
}
//_____________________________________________________________________________
void TGeoConeSeg::SetConsDimensions(Double_t dz, Double_t rmin1, Double_t rmax1,
Double_t rmin2, Double_t rmax2, Double_t phi1, Double_t phi2)
{
fDz = dz;
fRmin1 = rmin1;
fRmax1 = rmax1;
fRmin2 = rmin2;
fRmax2 = rmax2;
fPhi1 = phi1;
if (fPhi1<0) fPhi1+=360.;
fPhi2 = phi2;
while (fPhi2<fPhi1) fPhi2+=360.;
}
//_____________________________________________________________________________
void TGeoConeSeg::SetDimensions(Double_t *param)
{
Double_t dz = param[0];
Double_t rmin1 = param[1];
Double_t rmax1 = param[2];
Double_t rmin2 = param[3];
Double_t rmax2 = param[4];
Double_t phi1 = param[5];
Double_t phi2 = param[6];
SetConsDimensions(dz, rmin1, rmax1,rmin2, rmax2, phi1, phi2);
}
//_____________________________________________________________________________
void TGeoConeSeg::SetPoints(Double_t *points) const
{
// create cone segment mesh points
Int_t j, n;
Float_t dphi,phi,phi1, phi2,dz;
n = gGeoManager->GetNsegments()+1;
dz = fDz;
phi1 = fPhi1;
phi2 = fPhi2;
dphi = (phi2-phi1)/(n-1);
Int_t indx = 0;
if (points) {
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmin1 * TMath::Cos(phi);
points[indx++] = fRmin1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmax1 * TMath::Cos(phi);
points[indx++] = fRmax1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmin2 * TMath::Cos(phi);
points[indx++] = fRmin2 * TMath::Sin(phi);
points[indx++] = dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmax2 * TMath::Cos(phi);
points[indx++] = fRmax2 * TMath::Sin(phi);
points[indx++] = dz;
}
}
}
//_____________________________________________________________________________
void TGeoConeSeg::SetPoints(Float_t *points) const
{
// create cone segment mesh points
Int_t j, n;
Float_t dphi,phi,phi1, phi2,dz;
n = gGeoManager->GetNsegments()+1;
dz = fDz;
phi1 = fPhi1;
phi2 = fPhi2;
dphi = (phi2-phi1)/(n-1);
Int_t indx = 0;
if (points) {
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmin1 * TMath::Cos(phi);
points[indx++] = fRmin1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmax1 * TMath::Cos(phi);
points[indx++] = fRmax1 * TMath::Sin(phi);
points[indx++] = -dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmin2 * TMath::Cos(phi);
points[indx++] = fRmin2 * TMath::Sin(phi);
points[indx++] = dz;
}
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
points[indx++] = fRmax2 * TMath::Cos(phi);
points[indx++] = fRmax2 * TMath::Sin(phi);
points[indx++] = dz;
}
}
}
//_____________________________________________________________________________
Int_t TGeoConeSeg::GetNmeshVertices() const
{
// Return number of vertices of the mesh representation
Int_t n = gGeoManager->GetNsegments()+1;
Int_t numPoints = n*4;
return numPoints;
}
//_____________________________________________________________________________
void TGeoConeSeg::Sizeof3D() const
{
///// fill size of this 3-D object
/// TVirtualGeoPainter *painter = gGeoManager->GetGeomPainter();
/// if (!painter) return;
///
/// Int_t n = gGeoManager->GetNsegments()+1;
///
/// Int_t numPoints = n*4;
/// Int_t numSegs = n*8;
/// Int_t numPolys = n*4-2;
/// painter->AddSize3D(numPoints, numSegs, numPolys);
}
//_____________________________________________________________________________
const TBuffer3D & TGeoConeSeg::GetBuffer3D(Int_t reqSections, Bool_t localFrame) const
{
static TBuffer3D buffer(TBuffer3DTypes::kGeneric);
TGeoBBox::FillBuffer3D(buffer, reqSections, localFrame);
if (reqSections & TBuffer3D::kRawSizes) {
Int_t n = gGeoManager->GetNsegments()+1;
Int_t nbPnts = 4*n;
Int_t nbSegs = 2*nbPnts;
Int_t nbPols = nbPnts-2;
if (buffer.SetRawSizes(nbPnts, 3*nbPnts, nbSegs, 3*nbSegs, nbPols, 6*nbPols)) {
buffer.SetSectionsValid(TBuffer3D::kRawSizes);
}
}
if ((reqSections & TBuffer3D::kRaw) && buffer.SectionsValid(TBuffer3D::kRawSizes)) {
SetPoints(buffer.fPnts);
if (!buffer.fLocalFrame) {
TransformPoints(buffer.fPnts, buffer.NbPnts());
}
SetSegsAndPols(buffer);
buffer.SetSectionsValid(TBuffer3D::kRaw);
}
return buffer;
}