library: libHist
#include "TGraphDelaunay.h" |
TGraphDelaunay
class description - source file - inheritance tree (.pdf)
protected:
void CreateTrianglesDataStructure()
Bool_t Enclose(Int_t T1, Int_t T2, Int_t T3, Int_t Ex) const
void FileIt(Int_t P, Int_t N, Int_t M)
void FindHull()
Bool_t InHull(Int_t E, Int_t X) const
Double_t InterpolateOnPlane(Int_t TI1, Int_t TI2, Int_t TI3, Int_t E) const
public:
TGraphDelaunay()
TGraphDelaunay(TGraph2D* g)
TGraphDelaunay(const TGraphDelaunay&)
virtual ~TGraphDelaunay()
static TClass* Class()
Double_t ComputeZ(Double_t x, Double_t y)
void FindAllTriangles()
TGraph2D* GetGraph2D() const
Double_t GetMarginBinsContent() const
Int_t* GetMTried() const
Int_t GetNdt() const
Int_t* GetNTried() const
Int_t* GetPTried() const
Double_t* GetXN() const
Double_t GetXNmax() const
Double_t GetXNmin() const
Double_t* GetYN() const
Double_t GetYNmax() const
Double_t GetYNmin() const
Double_t Interpolate(Double_t x, Double_t y)
virtual TClass* IsA() const
TGraphDelaunay& operator=(const TGraphDelaunay&)
void SetMarginBinsContent(Double_t z = 0.)
void SetMaxIter(Int_t n = 100000)
virtual void ShowMembers(TMemberInspector& insp, char* parent)
virtual void Streamer(TBuffer& b)
void StreamerNVirtual(TBuffer& b)
protected:
Int_t fNdt !Number of Delaunay triangles found
Int_t fNpoints !Number of data points in fGraph2D
Int_t fNhull !Number of points in the hull
Double_t* fX !Pointer to fGraph2D->fX
Double_t* fY !Pointer to fGraph2D->fY
Double_t* fZ !Pointer to fGraph2D->fZ
Double_t* fXN !fGraph2D vectors normalized of size fNpoints
Double_t* fYN !fGraph2D vectors normalized of size fNpoints
Double_t fXNmin !Minimum value of fXN
Double_t fXNmax !Maximum value of fXN
Double_t fYNmin !Minimum value of fYN
Double_t fYNmax !Maximum value of fYN
Double_t fXoffset !
Double_t fYoffset !Parameters used to normalize user data
Double_t fScaleFactor !
Double_t fZout !Histogram bin height for points lying outside the convex hull
Double_t* fDist !Array used to order mass points by distance
Int_t fMaxIter !Maximum number of iterations to find Delaunay triangles
Int_t fTriedSize !Real size of the fxTried arrays
Int_t* fPTried !
Int_t* fNTried !Delaunay triangles storage of size fNdt
Int_t* fMTried !
Int_t* fHullPoints !Hull points of size fNhull
Int_t* fOrder !Array used to order mass points by distance
Bool_t fAllTri !True if FindAllTriangles() has been performed on fGraph2D
Bool_t fInit !True if CreateTrianglesDataStructure() and FindHull() have been performed
TGraph2D* fGraph2D !2D graph containing the user data
TGraphDelaunay generates a Delaunay triangulation of a TGraph2D. This
triangulation code derives from an implementation done by Luke Jones
(Royal Holloway, University of London) in April 2002 in the PAW context.
This software cannot be guaranteed to work under all circumstances. They
were originally written to work with a few hundred points in an XY space
with similar X and Y ranges.
Definition of Delaunay triangulation (After B. Delaunay):
For a set S of points in the Euclidean plane, the unique triangulation DT(S)
of S such that no point in S is inside the circumcircle of any triangle in
DT(S). DT(S) is the dual of the Voronoi diagram of S. If n is the number of
points in S, the Voronoi diagram of S is the partitioning of the plane
containing S points into n convex polygons such that each polygon contains
exactly one point and every point in a given polygon is closer to its
central point than to any other. A Voronoi diagram is sometimes also known
as a Dirichlet tessellation.
/*
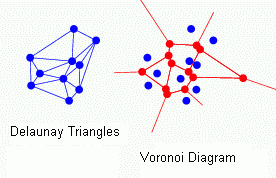
This applet
gives a nice practical view of Delaunay triangulation and Voronoi diagram.
*/
TGraphDelaunay()
: TNamed("TGraphDelaunay","TGraphDelaunay")
TGraphDelaunay default constructor
TGraphDelaunay(TGraph2D *g)
: TNamed("TGraphDelaunay","TGraphDelaunay")
TGraphDelaunay default constructor
~TGraphDelaunay()
TGraphDelaunay destructor.
Double_t ComputeZ(Double_t x, Double_t y)
Return the z value corresponding to the (x,y) point in fGraph2D
void CreateTrianglesDataStructure()
Fonction used internally only. It creates the data structures needed to
compute the Delaunay triangles.
Bool_t Enclose(Int_t t1, Int_t t2, Int_t t3, Int_t e) const
Is point e inside the triangle t1-t2-t3 ?
void FileIt(Int_t p, Int_t n, Int_t m)
Files the triangle defined by the 3 vertices p, n and m into the
fxTried arrays. If these arrays are to small they are automatically
expanded.
void FindAllTriangles()
Attempt to find all the Delaunay triangles of the point set. It is not
guaranteed that it will fully succeed, and no check is made that it has
fully succeeded (such a check would be possible by referencing the points
that make up the convex hull). The method is to check if each triangle
shares all three of its sides with other triangles. If not, a point is
generated just outside the triangle on the side(s) not shared, and a new
triangle is found for that point. If this method is not working properly
(many triangles are not being found) it's probably because the new points
are too far beyond or too close to the non-shared sides. Fiddling with
the size of the `alittlebit' parameter may help.
void FindHull()
Finds those points which make up the convex hull of the set. If the xy
plane were a sheet of wood, and the points were nails hammered into it
at the respective coordinates, then if an elastic band were stretched
over all the nails it would form the shape of the convex hull. Those
nails in contact with it are the points that make up the hull.
Bool_t InHull(Int_t e, Int_t x) const
Is point e inside the hull defined by all points apart from x ?
Double_t InterpolateOnPlane(Int_t TI1, Int_t TI2, Int_t TI3, Int_t e) const
Finds the z-value at point e given that it lies
on the plane defined by t1,t2,t3
Double_t Interpolate(Double_t xx, Double_t yy)
Finds the Delaunay triangle that the point (xi,yi) sits in (if any) and
calculate a z-value for it by linearly interpolating the z-values that
make up that triangle.
void SetMaxIter(Int_t n)
Defines the number of triangles tested for a Delaunay triangle
(number of iterations) before abandoning the search
void SetMarginBinsContent(Double_t z)
Sets the histogram bin height for points lying outside the convex hull ie:
the bins in the margin.
Inline Functions
TGraph2D* GetGraph2D() const
Double_t GetMarginBinsContent() const
Int_t GetNdt() const
Int_t* GetPTried() const
Int_t* GetNTried() const
Int_t* GetMTried() const
Double_t* GetXN() const
Double_t* GetYN() const
Double_t GetXNmin() const
Double_t GetXNmax() const
Double_t GetYNmin() const
Double_t GetYNmax() const
TClass* Class()
TClass* IsA() const
void ShowMembers(TMemberInspector& insp, char* parent)
void Streamer(TBuffer& b)
void StreamerNVirtual(TBuffer& b)
TGraphDelaunay TGraphDelaunay(const TGraphDelaunay&)
TGraphDelaunay& operator=(const TGraphDelaunay&)
Author: Olivier Couet, Luke Jones (Royal Holloway, University of London)
Last update: root/hist:$Name: $:$Id: TGraphDelaunay.cxx,v 1.00
Copyright (C) 1995-2000, Rene Brun and Fons Rademakers. *
ROOT page - Class index - Class Hierarchy - Top of the page
This page has been automatically generated. If you have any comments or suggestions about the page layout send a mail to ROOT support, or contact the developers with any questions or problems regarding ROOT.
