Simple Calculations
Equation Kinetic and Potential Energies
To better understand the many kinds of volcanoes, we can use some
math and the laws of physics. In an eruption, you can track a
"block" of volcanic material from some point where all of its
energy is potential energy and equate it at some other point
where it is at a maximum of kinetic energy:
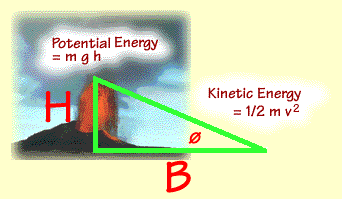
where m is the mass of the
"block", g is the gravity
acceleration constant, h is the
height where all energy is potential energy, and v is the velocity when the kinetic
energy is at a maximum.
Assuming conservation of energy, with some algebra we can write
this relationship as:
2 g h = v2
This means that if we know a height at which a volcanic flow
surmounted an obstacle, we can estimate its maximum velocity at
some point before or after the obstacle. This technique was used
to estimate the maximum flow velocity of a landslide in Iran that
climbed a 600 meter hill as well as a volcanic eruption in Japan
that climbed 500 meters over a mountain pass. The estimates are
supported by observations of these events.
Equation Kinetic and Potential Energies
Use the form below to calculate estimated maximum velocities for
volcanic eruptions where you can document how far they have
climbed (for large Plinian
eruptions, some researchers use the maximum height of the
eruption cloud).
Note that this is a very generalized way to look at volcanic
eruptions; i.e. it does not account for losses of energy due to
friction nor the different mechanics for fluid flow. However, it
has proven to be useful to compare different volcanoes.

